17-1 Careful measurements of the parallaxes of stars reveal their distances

The vast majority of stars are objects very much like the Sun. This understanding followed from the discovery that the stars are tremendously far from us, at distances so great that their light takes years to reach us. Because the stars at night are clearly visible to the naked eye despite these huge distances, it must be that the luminosity of the stars—that is, how much light energy they emit into space per second—is comparable to or greater than that of the Sun. Just as for the Sun, the only explanation for such tremendous luminosities is that thermonuclear reactions are occurring within the stars (see Section 16-1).

Clearly, then, it is important to know how distant the stars are. But how do we measure these distances? You might think these distances are determined by comparing how bright different stars appear. Perhaps the star Betelgeuse in the constellation Orion appears bright because it is relatively close, while the dimmer and less conspicuous star Polaris (the North Star, in the constellation Ursa Minor) is farther away.

But this line of reasoning is incorrect: Polaris is actually closer to us than Betelgeuse! How bright a star appears is not a good indicator of its distance. If you see a light on a darkened road, it could be a motorcycle headlight a kilometer away or a person holding a flashlight just a few meters away. In the same way, a bright star might be extremely far away but have an unusually high luminosity, and a dim star might be relatively close but have a rather low luminosity. Astronomers must use other techniques to determine the distances to the stars.

Parallax and the Distances to the Stars

The most straightforward way of measuring stellar distances uses an effect called parallax, which is the apparent displacement of an object because of a change in the observer’s point of view (Figure 17-1). To see how parallax works, hold your arm out straight in front of you. Now look at the hand on your outstretched arm, first with your left eye closed, then with your right eye closed. When you close one eye and open the other, your hand appears to shift back and forth against the background of more distant objects.

Figure 17-1: Parallax Imagine looking at some nearby object (a tree) against a distant background (mountains). When you move from one location to another, the nearby object appears to shift with respect to the distant background scenery. This familiar phenomenon is called parallax.

The closer the object you are viewing, the greater the parallax shift. To see this increased shift, repeat the experiment with your hand held closer to your face. Your brain analyzes such parallax shifts constantly as it compares the images from your left and right eyes, and in this way determines the distances to objects around you. This analysis is the basis for depth perception.

To measure the distance to a star, astronomers measure the parallax shift of the star using two points of view that are as far apart as possible—at opposite sides of Earth’s orbit. The direction from Earth to a nearby star changes as our planet orbits the Sun, and the nearby star appears to move back and forth against the background of more distant stars (Figure 17-2). This motion is called stellar parallax. The parallax (p) of a star is equal to half the angle through which the star’s apparent position shifts as Earth moves from one side of its orbit to the other. The larger the parallax p, the smaller the distance d to the star (compare Figure 17-2a with Figure 17-2b).

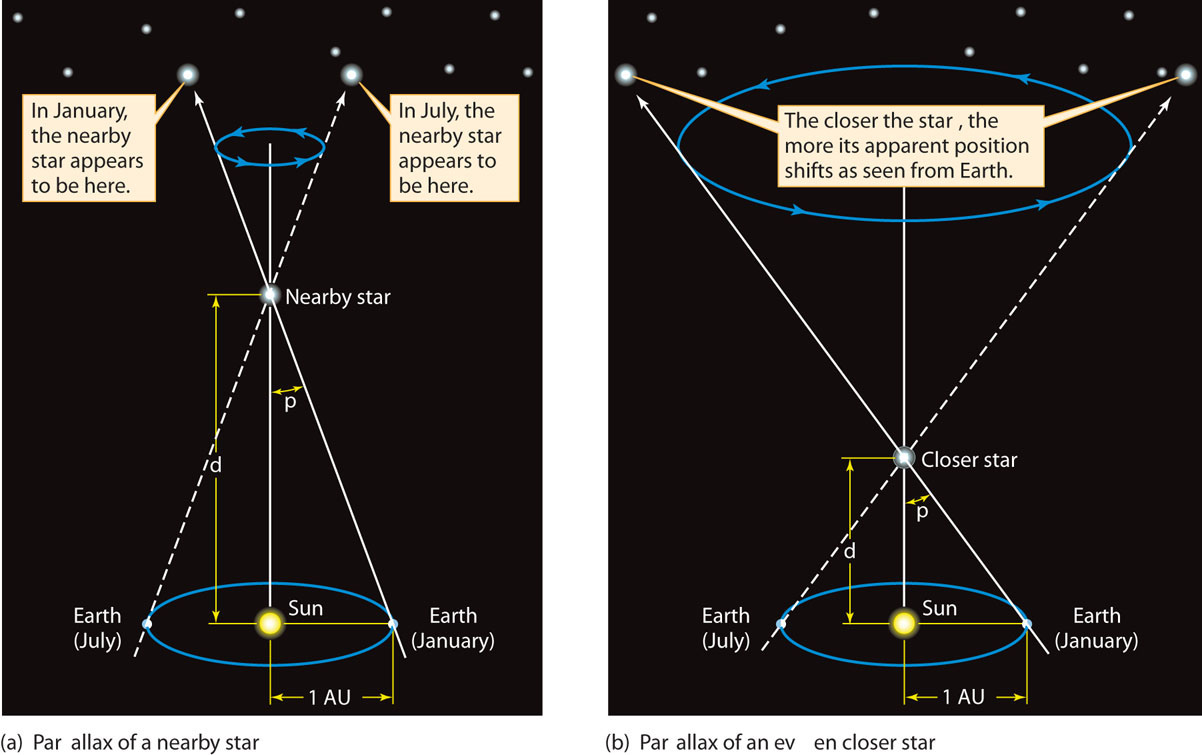
Figure 17-2: Stellar Parallax (a) As Earth orbits the Sun, a nearby star appears to shift its position against the background of distant stars. The parallax (p) of the star is equal to half the angle that the star appears to shift as Earth moves from one side of its orbit to the other. (b) The closer the star is to us, the greater the parallax angle p. The distance d to the star (in parsecs) is equal to the reciprocal of the parallax angle p (in arcseconds): d = 1/p.

It is convenient to measure the distance d in parsecs. A star with a parallax angle of 1 second of arc (p = 1 arcsec) is at a distance of 1 parsec (d = 1 pc). (The word “parsec” is a contraction of the phrase “the distance at which a star has a parallax of one arcsecond.” Recall from Section 1-7 that 1 parsec equals 3.26 ly, 3.09 × 10¹³ km, or 206,265 AU; see Figure 1-14.) If the angle p is measured in arcseconds, then the distance d to the star in parsecs is given by the following equation:

Relation between a star’s distance and its parallax

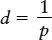
• d = distance to a star, in parsecs
• p = parallax angle of that star, in arcseconds

This simple relationship between parallax and distance in parsecs is one of the main reasons that astronomers usually measure cosmic distances in parsecs rather than light-years. For example, a star whose parallax is p = 0.1 arcsec is at a distance d = 1/(0.1) = 10 parsecs from Earth. Barnard’s star, named for the American astronomer Edward E. Barnard, has a parallax of 0.547 arcsec. Hence, the distance to this star is

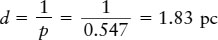
Because 1 parsec is 3.26 ly, this distance can also be expressed as

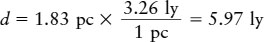
All known stars have parallax angles of less than 1 arcsecond. In other words, the closest star is more than 1 parsec away. Such small parallax angles are difficult to detect, so it was not until 1838 that the first successful parallax measurements were made by the German astronomer and mathematician Friedrich Wilhelm Bessel. He found the parallax angle of the star 61 Cygni to be just 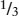arcsec—equal to the angular diameter of a dime at a distance of 11 km, or 7 mi. He thus determined that this star is about 3 pc from Earth. (Modern measurements give a slightly smaller parallax angle, which means that 61 Cygni is actually more than 3 pc away.) The star Proxima Centauri has the largest known parallax angle, 0.772 arcsec, and hence is the closest known star (other than the Sun); its distance is 1/(0.772) = 1.30 pc.

Appendix 4 at the back of this book lists all the stars within 4 pc of the Sun, as determined by parallax measurements. Most of these stars are far too dim to be seen with the naked eye, which is why their names are probably unfamiliar to you. By contrast, the majority of the familiar, bright stars in the nighttime sky (listed in Appendix 5) are so far away that their parallaxes cannot be measured from Earth’s surface. They appear bright not because they are close, but because they are far more luminous than the Sun. The brightest stars in the sky are not necessarily the nearest stars!

Measuring Parallax from Space

Parallax angles smaller than about 0.01 arcsec are extremely difficult to measure from Earth, in part because of the blurring effects of the atmosphere. Therefore, the parallax method used with ground-based telescopes can give fairly reliable distances only for stars nearer than about 1/0.01 = 100 pc. But an observatory in space is unhampered by the atmosphere. Observations made from spacecraft therefore permit astronomers to measure even smaller parallax angles and thus determine the distances to more remote stars.

In 1989 the European Space Agency (ESA) launched the satellite Hipparcos, an acronym for high precision parallax collecting satellite (and a commemoration of the ancient Greek astronomer Hipparchus, who created one of the first star charts). Over more than three years of observations, the telescope aboard Hipparcos was used to measure the parallaxes of 118,000 stars, some with an accuracy of 0.001 arcsecond. This telescope has enabled astronomers to determine stellar distances out to several hundred parsecs, and with much greater precision than has been possible with ground-based observations. In the years to come, astronomers will increasingly turn to space-based observations to determine stellar distances.

Unfortunately, most of the stars in the Galaxy are so far away that their parallax angles are too small to measure even with an orbiting telescope. Later in this chapter, we will discuss a technique that can be used to find the distances to these more remote stars. In Chapter 23 we will learn about other techniques that astronomers use to determine the much larger distances to galaxies beyond the Milky Way. These techniques also help us understand the overall size, age, and structure of the universe.

The Importance of Parallax Measurements

Because it can be used only on relatively close stars, stellar parallax might seem to be of limited usefulness. But parallax measurements are the cornerstone for all other methods of finding the distances to remote objects. These other methods require a precise and accurate knowledge of the distances to nearby stars, as determined by stellar parallax. Hence, any inaccuracies in the parallax angles for nearby stars can translate into substantial errors in measurement for the whole universe. To minimize these errors astronomers are continually trying to perfect their parallax-measuring techniques.

Figure 17-3: R I V U X G
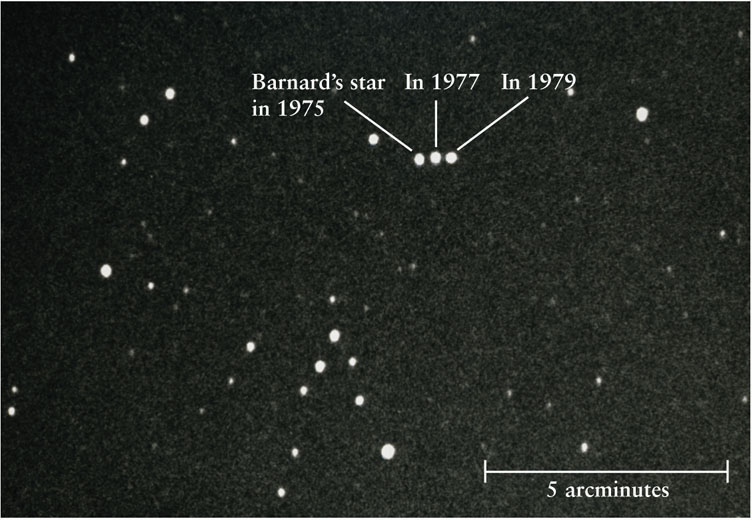
The Motion of Barnard’s Star Three photographs taken over a four-year period were combined to show the motion of Barnard’s star, which lies 1.82 pc away in the constellation Ophiuchus. Over this time interval, Barnard’s star moved more than 41 arcseconds on the celestial sphere (about 0.69 arcminutes, or 0.012°), more than any other star.

(John Sanford/Science Source)

Stellar parallax is an apparent motion of stars caused by Earth’s orbital motion around the Sun. But stars are not fixed objects, and they actually do move through space. As a result, stars change their positions on the celestial sphere (Figure 17-3), and they move either toward or away from the Sun. These motions are sufficiently slow, however, that changes in the positions of the stars are hardly noticeable over a human lifetime. Box 17-1 describes how astronomers study these motions and what insights they gain from these studies.

TOOLS OF THE ASTRONOMER’S TRADE

Stellar Motions

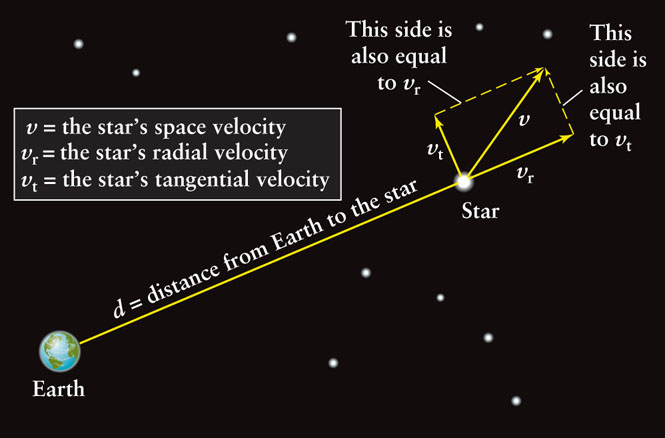
Stars can move through space in any direction. The space velocity of a star describes how fast and in what direction it is moving. As the accompanying figure shows, a star’s space velocity v can be broken into components parallel and perpendicular to our line of sight.

The component of velocity perpendicular to our line of sight—that is, across the plane of the sky—is called the star’s tangential velocity (v_t). To determine it, astronomers must know the distance to a star (d) and its proper motion (μ, the Greek letter mu), which is the number of arcseconds that the star appears to move per year on the celestial sphere. Proper motion does not repeat itself yearly, so it can be distinguished from the apparent back-and-forth motion due to parallax. In terms of a star’s distance and proper motion, its tangential velocity (in km/s) is

v_t = 4.74 μd

where μ is in arcseconds per year and d is in parsecs. For example, Barnard’s star (Figure 17-3) has a proper motion of 10.358 arcseconds per year and a distance of 1.83 pc. Hence, its tangential velocity is

v_t = 4.74(10.358)(1.83) = 89.8 km/s

The component of a star’s motion parallel to our line of sight—that is, either directly toward us or directly away from us—is its radial velocity (v_r). It can be determined from measurements of the Doppler shifts of the star’s spectral lines (see Section 5-9 and Box 5-6). If a star is approaching us, the wavelengths of all of its spectral lines are decreased (blueshifted); if the star is receding from us, the wavelengths are increased (redshifted). The radial velocity v_r is related to the wavelength shift by the equation

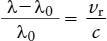
In this equation, λ is the wavelength of light coming from the star, λ₀ is what the wavelength would be if the star were not moving, and c is the speed of light. As an illustration, a particular spectral line of iron in the spectrum of Barnard’s star has a wavelength (λ) of 516.445 nm. As measured in a laboratory on Earth, the same spectral line has a wavelength (λ₀) of 516.629 nm. Thus, for Barnard’s star, our equation becomes

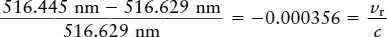
Solving this equation for the radial velocity v_r, we find

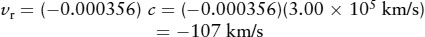
The minus sign means that Barnard’s star is moving toward us. You can check this interpretation by noting that the wavelength λ = 516.445 nm received from Barnard’s star is less than the laboratory wavelength λ₀ = 516.629 nm; hence, the light from the star is blueshifted, which indeed means that the star is approaching. If the star were receding, its light would be redshifted, and its radial velocity would be positive.

The illustration shows that the tangential velocity and radial velocity form two sides of a right triangle. The long side (hypotenuse) of this triangle is the space velocity (v). From the Pythagorean theorem, the space velocity is

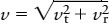
For Barnard’s star, the space velocity is

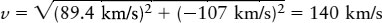
Therefore, Barnard’s star is moving through space at a speed of 140 km/s (503,000 km/h, or 312,000 mi/h) relative to the Sun.

Determining the space velocities of stars is essential for understanding the structure of the Galaxy. Studies show that the stars in our local neighborhood are moving in wide orbits around the center of the Galaxy, which lies some 8000 pc (26,000 ly) away in the direction of the constellation Sagittarius (the Archer). While many of the orbits are roughly circular and lie in nearly the same plane, others are highly elliptical or steeply inclined to the galactic plane. We will see in Chapter 22 how the orbits of stars and gas clouds reveal the Galaxy’s spiral structure.