17-6 Stars come in a wide variety of sizes and temperatures
A star’s radius can be calculated if we know its luminosity and surface temperature
With even the best telescopes, stars appear as nothing more than bright points of light. On a photograph or CCD image, brighter stars appear larger than dim ones (see Figure 17-3, Figure 17-6b, and Figure 17-13), but these apparent sizes give no indication of the star’s actual size. To determine the size of a star, astronomers combine information about its luminosity (determined from its distance and apparent brightness) and its surface temperature (determined from its spectral type). In this way, they find that some stars are quite a bit smaller than the Sun, while others are a thousand times larger.
Calculating the Radii of Stars
The key to finding a star’s radius from its luminosity and surface temperature is the Stefan-Boltzmann law (see Section 5-4). This law says that the amount of energy radiated per second from a square meter of a blackbody’s surface—that is, the energy flux (F)—is proportional to the fourth power of the temperature of that surface (T), as given by the equation F = σT4. This equation applies very well to stars, whose spectra are quite similar to that of a perfect blackbody. (Absorption lines, while important for determining the star’s chemical composition and surface temperature, make only relatively small modifications to a star’s blackbody spectrum.)
A star’s luminosity is the amount of energy emitted per second from its entire surface. This quantity equals the energy flux F multiplied by the total number of square meters on the star’s surface (that is, the star’s surface area). We expect that most stars are nearly spherical, like the Sun, so we can use the formula for the surface area of a sphere. The formula is 4πR2, where R is the star’s radius (the distance from its center to its surface). Multiplying together the formulas for energy flux and surface area, we can write the star’s luminosity as follows:
Relationship between a star’s luminosity, radius, and surface temperature
L = 4πR2σT4
- L = star’s luminosity, in watts
- R = star’s radius, in meters
- σ = Stefan-Boltzmann constant = 5.67 × 10−8 W m−2 K−4
- T = star’s surface temperature, in kelvins
This equation says that a relatively cool star (low surface temperature T), for which the energy flux is quite low, can nonetheless be very luminous if it has a large enough radius R. Alternatively, a relatively hot star (large T) can have a very low luminosity if the star has only a little surface area (small R).
484
Box 17-4 describes how to use the above equation to calculate a star’s radius if its luminosity and surface temperature are known.
TOOLS OF THE ASTRONOMER’S TRADE
Stellar Radii, Luminosities, and Surface Temperatures
Because stars emit light in almost exactly the same fashion as blackbodies, we can use the Stefan-Boltzmann law to relate a star’s luminosity (L), surface temperature (T), and radius (R). The relevant equation is
L = 4πR2σT4
As written, this equation involves the Stefan-Boltzmann constant σ, which is equal to 5.67 × 10−8 W m−2 K−4. In many calculations, it is more convenient to relate everything to the Sun, which is a typical star. Specifically, for the Sun we have L⊙ = 4πR⊙2σT⊙4, where L⊙ is the Sun’s luminosity, R⊙ is the Sun’s radius, and T⊙ is the Sun’s surface temperature (equal to 5800 K). Dividing the general equation for L by this specific equation for the Sun, we obtain
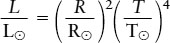
This formula is easier to use because the constant σ has cancelled out. We can also rearrange terms to arrive at a useful equation for the radius (R) of a star:
Radius of a star related to its luminosity and surface temperature
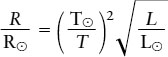
EXAMPLE: The bright reddish star Betelgeuse in the constellation Orion (see Figure 2-2) is 60,000 times more luminous than the Sun and has a surface temperature of 3500 K. What is its radius?
Situation: We are given the star’s luminosity L = 60,000 L⊙ and its surface temperature T = 3500 K. Our goal is to find the star’s radius R.
Tools: We use the above equation to find the ratio of the star’s radius to the radius of the Sun, R/R⊙. Note that we also know the Sun’s surface temperature, T⊙ = 5800 K.
Answer: Substituting these data into the above equation, we get
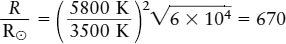
Review: Our result tells us that Betelgeuse’s radius is 670 times larger than that of the Sun. The Sun’s radius is 6.96 × 105 km, so we can also express the radius of Betelgeuse as (670)(6.96 × 105 km) = 4.7 × 108 km, which is more than 3 AU. If Betelgeuse were located at the center of our solar system, it would extend beyond the orbit of Mars!
EXAMPLE: Sirius, the brightest star in the sky, is actually two stars orbiting each other (a binary star). The less luminous star, Sirius B, is a white dwarf that is too dim to see with the naked eye. Its luminosity is 0.0025 L⊙ and its surface temperature is 10,000 K. How large is Sirius B compared to Earth?
Situation: Again we are asked to find a star’s radius from its luminosity and surface temperature.
Tools: We use the same equation as in the preceding example.
Answer: The ratio of the radius of Sirius B to the Sun’s radius is
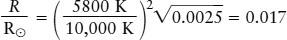
Since the Sun’s radius is R⊙ = 6.96 × 105 km, the radius of Sirius B is (0.017)(6.96 × 105 km) = 12,000 km. From Table 7-1, Earth’s radius (half its diameter) is 6378 km. Hence, this star is only about twice the radius of Earth.
Review: Sirius B’s radius would be large for a terrestrial planet, but it is minuscule for a star. The name dwarf is well deserved!
The radii of some stars have been measured with other techniques (see Section 17-11). These other methods yield values consistent with those calculated by the methods just described.
We can express the idea behind these calculations in terms of the following general rule:
We can determine the radius of a star from its luminosity and surface temperature.
For a given luminosity: The greater the surface temperature, the smaller the radius must be.
For a given surface temperature: The greater the luminosity, the larger the radius must be.
ANALOGY
In a similar way, a roaring campfire can emit more light than a welder’s torch. The campfire is at a lower temperature than the torch, but has a much larger surface area from which it emits light.
The Range of Stellar Radii
Using this general rule as shown in Box 17-4, astronomers find that stars come in a wide range of sizes. The smallest stars visible through ordinary telescopes, called white dwarfs, are about the same size as Earth. Although their surface temperatures can be very high (25,000 K or more), white dwarfs have so little surface area that their luminosities are very low (less than 0.01 L⊙). The largest stars, called supergiants, are a thousand times larger in radius than the Sun and 105 times larger than white dwarfs. If our own Sun were replaced by one of these supergiants, Earth’s orbit would lie completely inside the star!
Figure 17-14 summarizes how astronomers determine the distance from Earth, luminosity, surface temperature, chemical composition, and radius of a star close enough to us so that its parallax can be measured. Remarkably, all of these properties can be deduced from just a few measured quantities: the star’s parallax angle, apparent brightness, and spectrum.
CONCEPT CHECK 17-12
What makes lighting a candle using a large, roaring bonfire much more difficult than using a handheld lighter of the same temperature?
CALCULATION CHECK 17-4
If two stars are at the same temperature, but one is 3 times larger, how many times more luminous is it?