21-1 The special theory of relativity changes our conceptions of space and time
The idea of a black hole is a truly strange one. To appreciate it, we must discard some “commonsense” notions about the nature of space and time.
The Special Theory of Relativity
According to the classical physics of Newton, space is perfectly uniform and fills the universe like a rigid framework. Similarly, time passes at a monotonous, unchanging rate. It is always possible to know exactly how fast you are moving through this rigid fabric of space and time.
To understand black holes, we must first grasp the nature of space and time as described by Einstein’s special theory of relativity
Those ideas were upset forever in 1905 when Albert Einstein proposed his special theory of relativity. This theory describes how motion affects our measurements of distance and time. It is “special” in the sense of being specialized. In particular, it does not include the effects of gravity. The word “relativity” is used because one of the key ideas of the theory is that all measurements are made relative to an observer. Contrary to Newton, there is no absolute framework of space and time.
In particular, the distance between two points is not an absolute, nor is the time interval between two events. Instead, the values that you measure for these quantities depend on how you are moving, and these values are relative to you. Thus, one of Einstein’s key discoveries is that someone moving in a different way would measure different lengths for objects and different durations of events. In our everyday experience we do not notice that time and distance measurements depend on the speed between an observer and the events being observed because, as we will see, these effects are most noticeable when that speed approaches the speed of light.
Remarkably, Einstein’s theory is based on just two basic principles. The first is quite simple:
Your description of physical reality is the same, regardless of the constant velocity at which you move.
In other words, if you are moving in a straight line at a constant speed, you experience the same laws of physics as you would if you were moving at any other constant speed and in any other direction. As an example, suppose you were inside a closed railroad car moving due north in a straight line at 100 km/h. Any measurements you make inside the car—for example, how long your thumb is or how long it takes for a ball to drop to the floor—will give exactly the same results as if the car were moving in any other direction or at any other speed, or were not moving at all. This first principle is what we experience in everyday life when riding on a bus or flying on an airplane: Phenomena inside a flying airplane (such as dropping a book) appear the same as when the plane is on the ground even though we are moving, and this would still be true if the plane could fly near the speed of light.
CAUTION!
You might think there is a contradiction between the two statements that (1) measurements of the same event (such as dropping a ball) inside the railroad car give the same results regardless of the train’s speed, and that (2) motion between an observer and events changes the times and distances being observed, and that someone moving in a different way could measure different values. To understand these statements, think of the train car as a laboratory, and one observer is inside moving right along with the experiments being conducted. The first statement says that you can move the laboratory at any speed and it will not change what the observer inside measures. The second statement—a primary result of special relativity—refers to differences between two observers. If a second observer standing on the train tracks takes measurements of the experiments taking place in the train (perhaps looking through a window), the two observers are moving at different speeds with respect to the experiment, and they can measure different values for some of the phenomena. Again, this discrepancy between observers is most noticeable when the speed between them is near the speed of light.
Einstein’s second principle is much more bizarre than the first:
Regardless of your speed or direction of motion, you always measure the speed of light to be the same.
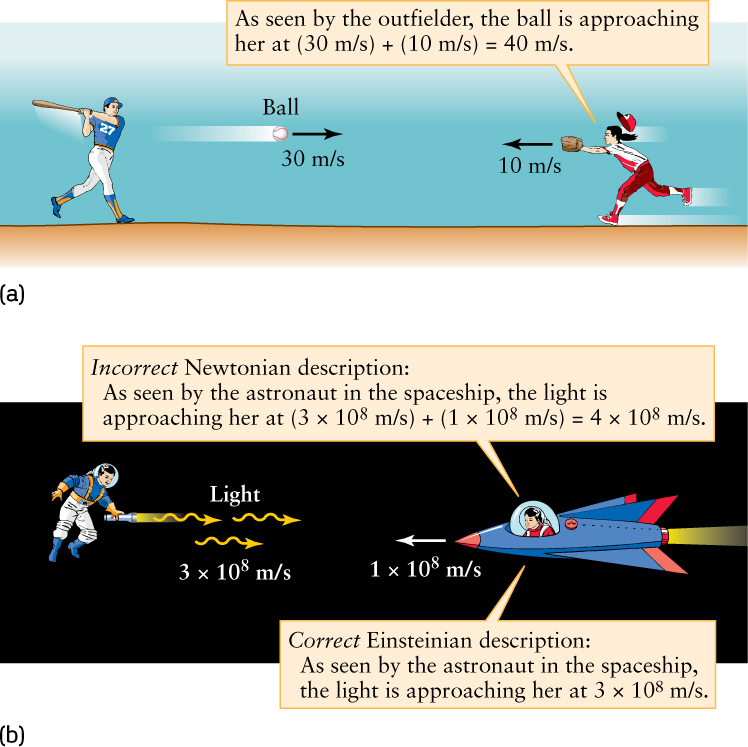
To see what this implies, imagine that you are in a spaceship that is moving toward a flashlight. Even if you are moving at 99% of the speed of light, you will measure the photons from the flashlight to be moving at the same speed (c = 3 × 108 m/s = 3 × 105 km/s) as if your spaceship were motionless. This statement is in direct conflict with the Newtonian view that a stationary person and a moving person should measure different speeds (Figure 21-1).
Speed involves both distance and time. Since speed has a very different behavior in the special theory of relativity than in Newton’s physics, it follows that both space and time behave differently as well. Indeed, in relativity, time proves to be so intimately intertwined with the three dimensions of space that we regard them as a single four-dimensional entity called spacetime.
Length Contraction
Einstein expressed his ideas about spacetime in a mathematical form and used this description to make a number of predictions about nature. All these predictions have been verified in innumerable experiments. One prediction is that the length you measure an object to have depends on how that object is moving; the faster it moves, the shorter its length along its direction of motion (Figure 21-2). This is called length contraction. In other words, if a railroad car moves past you at high speed, from your perspective on the ground you will actually measure it to be shorter than if it were at rest (Figure 21-2a). However, if you are on board the railroad car and moving with it, you will measure its length to be the same as measured on the ground when it was at rest. The word “relativity” emphasizes the importance of the relative speed between the observer and the object being measured.
605
If the idea of length contraction seems outrageous, it is because this effect is noticeable only at very high speeds, near the speed of light. But even the fastest spacecraft ever built by humans travels at a mere 1/25,000 of the speed of light. At this speed, a spacecraft 10 m long would be contracted in length by only 8 nm—a distance equal to the width of a single protein molecule! For moving cars, trains, and airplanes, length contraction is far too small to measure. As Box 21-1 describes, however, we can easily see the effects of length contraction for subatomic particles that do indeed travel at nearly the speed of light.
Time Dilation
A second result of relativity is no less strange: A clock moving past you runs more slowly than a clock that is at rest. Like length contraction, this time dilation is a very small effect unless the clock is moving at extremely high speeds (Figure 21-2b). Nonetheless, physicists have confirmed the existence of time dilation by using an extremely accurate atomic clock carried on a jet airliner. When the airliner landed, they found that the on-board clock had actually ticked off slightly less time than an identical, stationary clock on the ground. For the passengers on board the airliner during this experiment, however, time flowed at a normal rate: The on-board clock ticked off the seconds as usual, their hearts beat at a normal rate, and so on. You only measure a clock (or a beating heart) to be running slow if it is moving relative to you. Box 21-1 discusses time dilation in more detail.
606
TOOLS OF THE ASTRONOMER’S TRADE
Time Dilation and Length Contraction
The special theory of relativity describes how motion affects measurements of time and distance. By using the two basic principles of his theory—that no matter how fast you move, the laws of physics and the speed of light are the same—Einstein concluded that measurements of time and distance must depend on how the person making the measurements is moving.
To describe how measurements depend on motion, Einstein derived a series of equations named the Lorentz transformations, after the famous Dutch physicist Hendrik Antoon Lorentz. (Lorentz was a contemporary of Einstein who developed these equations independently but did not grasp their true meaning.) These equations tell us exactly how moving clocks slow down and how moving objects shrink.
To appreciate the Lorentz transformations, imagine two observers named Sergio and Majeeda. Sergio is at rest on Earth, while Majeeda is flying past in her spaceship at a speed v. Sergio and Majeeda both observe the same phenomenon on Earth—say, the beating of Sergio’s heart or the ticking of Sergio’s watch— which appears to occur over an interval of time. According to Sergio’s clock (which is not moving relative to the phenomenon), the phenomenon lasts for T0 seconds. This time period is called the proper time of the phenomenon. But according to Majeeda’s clock (which is moving relative to the phenomenon), the same phenomenon lasts for a different length of time, T seconds. These two time intervals are related as follows:
Lorentz transformation for time
T = time interval measured by an observer moving relative to the phenomenon
T0 = time interval measured by a observer not moving relative to the phenomenon (proper time)
v = speed of the moving observer relative to the phenomenon
c = speed of light
EXAMPLE: Sergio heats a cup of water in a microwave oven for 1 minute. According to Majeeda, who is flying past Sergio at 98% of the speed of light, how long does it take to heat the water?
Situation: The phenomenon in question is heating the water in the microwave oven. Sergio is not moving relative to this phenomenon (so he measures the proper time interval T0). Majeeda is moving at speed v = 0.98c relative to this phenomenon (so she measures a different time interval T). Our goal is to determine the value of T.
Tools: We use the Lorentz transformation for time to calculate T.
Answer: We have v/c = 0.98, so
Review: A phenomenon that lasts for T0 = 1 minute on Sergio’s clock is stretched out to T = 5T0 = 5 minutes as measured on Majeeda’s clock moving at 98% of the speed of light. Other phenomena are affected in the same way: As measured by Majeeda, it takes 5 seconds for Sergio’s wristwatch to tick off one second, and the minute hand on Sergio’s wristwatch takes 5 hours to make a complete sweep. The converse is also true. As measured by Sergio, the minute hand on Majeeda’s wristwatch will take 5 hours to make a complete sweep. This phenomenon, in which events moving relative to an observer happen at a slower pace, is called time dilation.
The Lorentz transformation for time is plotted in Figure 21-2b, which shows how 1 second measured on a stationary clock (say, Sergio’s) is stretched out when measured using a clock carried by a moving observer (such as Majeeda). For speeds less than about half the speed of light, the mathematical factor 
is not too different from 1, and there is little difference between the recordings of the stationary and moving clocks. At the fastest speeds that humans have ever traveled (en route from Earth to the Moon), the difference between 1 and the factor
is less than 10−9. So, for any speed associated with human activities, stationary and slowly moving clocks tick at essentially the same rate. As the next example shows, however, time dilation is important for subatomic particles that travel at speeds comparable to c.
EXAMPLE: When unstable particles called muons (pronounced “mew-ons”) are produced in experiments on Earth, they decay into other particles in an average time of 2.2 × 10−6 s. Muons are also produced by fast-moving protons from interstellar space when they collide with atoms in Earth’s upper atmosphere. These muons typically move at 99.9% of the speed of light and are formed at an altitude of 10 km. How long do such muons last before they decay?
Situation: The phenomenon in question is the life of a muon, which lasts a time T0 = 2.2 × 10−6 s as measured by an observer not moving with respect to the muon. Our goal is to find the time interval T measured by an observer on Earth, which is moving at v = 0.999c relative to the muon (the same speed at which the muon is moving relative to Earth).
607
Tools: As in the previous example, we use the Lorentz transformation for time.
Answer: Using v/c = 0.999,
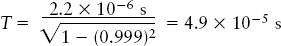
Review: At this speed, the muon’s lifetime is slowed down by time dilation by a factor of more than 22. Note that as measured by an observer on Earth, the time that it takes a muon produced at an altitude of 10 km = 10,000 m to reach Earth’s surface is
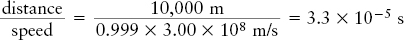
Were there no time dilation, such a muon would decay in just 2.2 × 10−6 s and would never reach Earth’s surface. But in fact, these muons are detected by experiments on Earth’s surface, because a muon moving at 0.999c lasts more than 3.3 × 10−5 s. The detection at Earth’s surface of muons from the upper atmosphere is compelling evidence for the reality of time dilation.
In the same terminology as “proper time,” we say that a ruler at rest measures proper length or proper distance (L0). According to the Lorentz transformations, distances perpendicular to the direction of motion are unaffected. However, a ruler of proper length L0 held parallel to the direction of motion shrinks to a length L, given by
Lorentz transformation for length
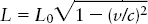
L = length of a moving object along the direction of motion
L0 = length of the same object at rest (proper length)
v = speed of the moving object
c = speed of light
EXAMPLE: Again, imagine that Majeeda is traveling at 98% of the speed of light relative to Sergio. If Majeeda holds a 1-m ruler parallel to the direction of motion, how long is this ruler as measured by Sergio?
Situation: The ruler is at rest relative to Majeeda, so she measures its proper length L0 = 1 m. Our goal is to determine its length L as measured by Sergio, who is moving at v = 0.98c relative to Majeeda and her ruler.
Tools: We use the Lorentz transformation for length.
Answer: With v/c = 0.98, we find
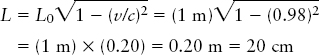
Review: We saw in the first example that according to Sergio, Majeeda’s clocks are ticking only one-fifth as fast as his. This example shows that he also measures Majeeda’s 1-m ruler to be only one-fifth as long (20 cm) when held parallel to the direction of motion. Note that the converse is also true: If Sergio holds a 1-m ruler parallel to the direction of relative motion, Majeeda measures it to be only 20 cm long. This shrinkage of length is called length contraction.
EXAMPLE: Consider again the above example about muons created 10 km above Earth’s surface. If a muon is traveling straight down, what is the distance to the surface as measured by an observer riding along with the muon?
Situation: Imagine a ruler that extends straight up from Earth’s surface to where the muon is formed. This ruler is at rest relative to Earth, so its length of 10 km is the proper length L0. Our goal is to find the length L of this ruler as measured by the observer riding with the muon.
Tools: As in the previous example, we use the Lorentz transformation for length.
Answer: With v/c = 0.999, we calculate
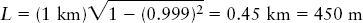
Review: The distance is contracted tremendously as measured by an observer riding with the muon. This result gives us another way to explain how such muons are able to reach Earth’s surface. As measured by the muon, the time required to travel the contracted distance is
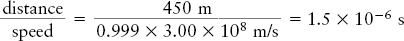
This time is less than the 2.2 × 10−6 s that an average muon takes to decay. Hence, muons can successfully reach Earth’s surface.
608
As an example of the time dilation in Figure 21-2b, suppose a rider on the train has a heart that beats once per second. Any method used to measure the rider’s heartbeat on the train gives this value—1 second between beats. Perhaps watching through a window, consider a nurse on the tracks observing the rider’s heartbeat as the hypothetical train speeds by at 98% of the speed of light (labeled 0.98c in the figure). In Figure 21-2b, we see that from the tracks, the nurse would measure that the rider’s heart only beat once every 5 seconds on the nurse’s own clock. In other words, the stationary observer would see a slower heartbeat.
The special theory of relativity predicts that the astronaut with the flashlight in Figure 21-1b sees the astronaut flying in the spaceship as shortened along the direction of motion and as having slowly ticking clocks. Remarkably, it also says that the flying astronaut sees the astronaut with the flashlight (who is moving relative to her) as being shortened and as having slowly ticking clocks! These observations may seem contradictory, but they are not: Each spaceship is moving relative to the other, and in the special theory of relativity only relative motion matters. Each astronaut’s measurements are correct relative to his or her frame of reference.
Now we see the significance of relative motion between observers. Relative motion changes what observers measure for certain quantities, such as length and time. Objects observed in motion are shorter in their direction of motion, and clocks observed in motion tick more slowly. However, relative motion does not change the speed of light (through empty space) and it does not change the laws used to describe nature.
CAUTION!
You may have the idea that the special theory of relativity implies that there are no absolutes in nature and that everything is relative. But, in fact, the special theory is based on the principles that the laws of physics and the speed of light in a vacuum are absolutes. Only certain quantities, such as distance and time, depend on your state of motion. You may also have the idea that length contraction and time dilation are just optical illusions caused by high speeds. But these effects are real. A moving spaceship does not just look shorter or seem to be shorter—it really is shorter. Likewise, a moving clock does not merely look like it is ticking slowly, or seem to be ticking slowly—it really does tick more slowly. Einstein’s theory is supported by every experiment designed to test it. Relativity is very strange, but it is also very real!
CONCEPT CHECK 21-1
Suppose you are on the hypothetical train in Figure 21-2a. If the train sped along at half the speed of light, would it appear to you that the train contracts in length? Would your heart beat more slowly?
CONCEPT CHECK 21-2
Suppose two spaceships travel directly toward each other at 90% the speed of light relative to an observer watching from a planet right in the middle of the spaceships. Each spaceship turns on its lights for everyone to see. At what speed does a traveler from one spaceship see light arriving from the other spaceship? At what speed does the observer on the planet see light arriving from the spaceship?
Mass and Energy
Einstein’s special theory of relativity predicts another famous relationship: Any object with mass (m) has energy (E) embodied in its mass. This idea is expressed by the well-known formula E = mc2, where c is the speed of light. In thermonuclear reactions, part of the energy embodied in the mass of atomic nuclei is converted into other forms of energy. This released energy is what makes the Sun and the stars shine (see Section 16-1). The conversion of mass into energy results in a real loss of mass; as the Sun shines it loses about 100 times the mass of the largest Egyptian pyramid each second. The sunlight we see by day and the starlight that graces our nights are a brilliant verification of the special theory of relativity.
The special theory of relativity also explains why it is impossible for a spaceship to move at the speed of light. If it could, then a light beam traveling in the same direction as the spaceship would appear to the ship’s crew to be stationary. But this would contradict the second of Einstein’s principles, which says that all observers, including those on a spaceship, must see light traveling at the speed of light. Therefore, it cannot be possible for a spaceship to travel at the speed of light. In fact, no object with mass can travel at the speed of light. This conclusion has also been verified by experiments. Subatomic particles can be made to travel at 99.99999999% of the speed of light c, but they can never make it all the way to c.