21-6 A nonrotating black hole has only a “center” and a “surface”
Understanding in detail how black holes form is a challenging task. But once a black hole forms, it has a remarkably simple structure.
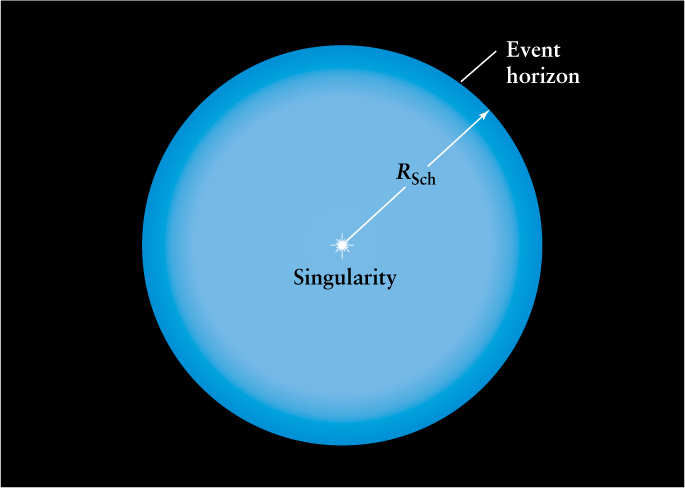
Recall from Section 21-2, a black hole is an object with an escape speed greater than the speed of light. Since nothing can travel faster than the speed of light, nothing can escape a black hole. Even light can’t escape, which is how black holes got their name. A black hole has no surface, but instead has a spherical boundary called the event horizon where the escape speed just equals the speed of light. Once the core of a massive dying star collapses to within its event horizon, it disappears permanently from the universe.
CAUTION!
A black hole does not suck in everything from its surroundings. While anything that crosses the event horizon is lost forever, material outside the event horizon traveling at high speeds can pass by without getting trapped. Far away from a black hole, the black hole is like any other object. As mentioned earlier, if the Sun became a black hole, the planets are all too far away for any noticeable orbital effects.
If the dying star is not rotating before it collapses, the black hole will likewise not be rotating. We will consider these nonrotating black holes first, and then consider rotating black holes in the next section. The distance from the center of a nonrotating black hole to its event horizon is called the Schwarzschild radius (denoted RSch), after the German physicist Karl Schwarzschild who first determined its properties. Box 21-2 describes how to calculate the Schwarzschild radius, which depends only on the black hole’s mass. The more massive the black hole, the larger its event horizon.
Inside a Black Hole
All of the mass of a nonrotating black hole is concentrated nearly to a point at the center called the singularity
Once an object (such as a stellar core) has contracted enough to form an event horizon, nothing can prevent the matter’s further collapse. Equations describing the matter within the event horizon indicate that the object’s entire mass is crushed nearly to a single point, known as the singularity, at the center of the black hole. We now can see that the structure of a nonrotating black hole is quite simple. As drawn in Figure 21-17, it has only two parts: a singularity at the center surrounded by a spherical event horizon. Note that while a black hole’s effects on space and time away from the singularity are fairly well understood, the singularity itself—with its nearly infinite density—poses both mathematical and conceptual problems in physics.
BOX 21-2 TOOLS OF THE ASTRONOMER’S TRADE
The Schwarzschild Radius
The Schwarzschild radius (RSch) is the distance from the center of a nonrotating black hole to its event horizon. You can think of this radius as the “size” of the black hole. For an object of a given mass, the Schwarzschild radius is the size that mass would need to be concentrated within, in order to make the escape speed from that object equal to the speed of light. The Schwarzschild radius is related to the mass M of the black hole by
Schwarzschild radius
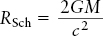
RSch = Schwarzschild radius of a black hole
G = universal constant of gravitation
M = mass of black hole
c = speed of light
When using this formula, be careful to express the mass in kilograms, not solar masses, because of the units in which G and c are commonly expressed (G = 6.67 × 10−11 Nm2/kg2 and c = 3.00 × 108 m/s). If you use M in kilograms, the answer that you get for RSch will be in meters.
EXAMPLE: Find the Schwarzschild radius (in kilometers) of a black hole with 10 times the mass of the Sun.
Situation: We are given the mass of the black hole (10 M⊙) and wish to determine its Schwarzschild radius RSch.
Tools: We use the above formula for RSch, being careful to first convert the mass from solar masses to kilograms.
Answer: One solar mass is 1.99 × 1030 kg, so in this case M = 10 × 1.99 × 1030 kg = 1.99 × 1031 kg. The Schwarzschild radius of this black hole is then
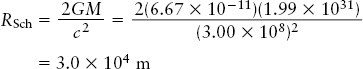
One kilometer is 103 m, so the Schwarzschild radius of this 10-M⊙ black hole is
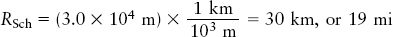
Review: The Schwarzschild radius is directly proportional to the mass of the black hole. Thus, a black hole with 10 times the mass (100 M⊙) would have a Schwarzschild radius 10 times larger (RSch = 10 × 30 km = 300 km); a black hole with half the mass (5 M⊙) would have half as large a Schwarzschild radius (RSch = 1/2 × 30 km = 15 km), and so on.
As seen in Box 21-2, the size—called the Schwarzschild radius—is given for a massive object to form a black hole. For larger mass black holes, this size corresponds to lower average densities than for smaller mass black holes: As noted in Section 21-5, a supermassive black hole could be formed by a solar system filled with water. However, once a black hole forms, its mass rapidly collapses toward the center. So, while less extreme conditions are required to form supermassive black holes, the conditions inside all black holes are extreme.
To understand why the complete collapse of such a doomed star is inevitable, first think about your own life on Earth, far from any black holes. You have the freedom to move as you wish through the three dimensions of space: up and down, left and right, or forward and back. But you do not have the freedom to move at will through the dimension of time. Whether we like it or not, we are all carried inexorably through time from the cradle to the grave.
Inside a black hole, gravity distorts the structure of spacetime so severely that the directions of space and time become interchanged. In a sense, inside a black hole you acquire a limited ability to affect the passage of time. This apparent gain does you no good, however, because you lose a corresponding amount of freedom to move through space. Whether you like it or not, you will be dragged inexorably from the event horizon toward the singularity. Just as no force in the universe can prevent the forward march of time from past to future outside a black hole, no force in the universe can prevent the inward march of matter from the event horizon to the singularity inside a black hole. Once an object dropped into a black hole crosses the event horizon, it is gone forever, like an object dropped into a bottomless pit.
The same is true for a light beam aimed at the black hole. Because all this light will be absorbed and none reflected back, a black hole is indeed black. By contrast, even the blackest object on Earth reflects some light when you shine a flashlight on it—a black hole would reflect none. (In Section 21-9 we will see that black holes are expected to emit some particles and light through a quantum physics process, but this radiation arises just outside the event horizon and would be negligible for black holes of stellar-mass size or larger.)
Although black holes are really very intriguing objects, there are some common misconceptions about their nature. The Cosmic Connections: Black Hole “Urban Legends” exposes two of these misconceptions.
COSMIC CONNECTIONS

CONCEPT CHECK 21-11
What is the connection between a black hole’s Schwarzschild radius and its event horizon?
A black hole’s event horizon is a spherical boundary with a radius given by the Schwarzschild radius. Objects getting closer to the Schwarzschild radius have fallen irreversibly within the event horizon.
CONCEPT CHECK 21-12
Consult the Cosmic Connections: Urban Legend #1 figure. Consider being 10 million km from the Sun, and then the same distance from a black hole of 1 M⊙. From which object do you feel a greater gravitational force?
At such large distances, the gravitational force is the same from each object. Stronger forces and other effects only show up much closer to a black hole.
CONCEPT CHECK 21-13
Consult the Cosmic Connections: Urban Legend #2 figure. If you had a personal rocket spacecraft that was low on gas, would it be safer to fly by the event horizon of a small black hole or a large black hole?
It would be safer to fly by the event horizon of the larger black hole, where the gravitational force is actually weaker.