6-1 A refracting telescope uses a lens to concentrate incoming light at a focus
Refracting telescopes gave humans the first close-up views of the Moon and planets
The optical telescope—that is, a telescope designed for use with visible light—was invented in the Netherlands in the early seventeenth century. Soon after, Galileo used one of these new inventions for his groundbreaking astronomical observations (see Section 4-5). These first telescopes used carefully shaped pieces of glass, or lenses, to make distant objects appear larger and brighter. Telescopes of this same basic design are used today by many amateur astronomers. To understand telescopes of this kind, we need to understand how lenses work.
Refraction of Light
Lenses used in telescopes gather and focus light. Larger lenses can gather more light, which is why professional telescopes must be big. Focusing light requires that the light’s path be bent. The ability of a lens to bend light is based on a universal fact: Light travels at a slower speed in a dense substance.
Thus, although the speed of light in a vacuum is 3.00 × 108 m/s, its speed in glass is less than 2 × 108 m/s. Just as a woman’s walking pace slows suddenly when she walks from a boardwalk onto a sandy beach, so light slows abruptly as it enters a piece of glass. The same woman easily resumes her original pace when she steps back onto the boardwalk; in the same way, light resumes its original speed upon exiting the glass.
A material through which light travels is called a medium (plural media). As a beam of light passes from one transparent medium into another—say, from air into glass, or from glass back into air—the direction of the light can change. This path-bending phenomenon, called refraction, is caused by the change in the speed of light.
ANALOGY
Imagine driving a car from a smooth pavement onto a sandy beach (Figure 6-1a). If the car approaches the beach head-on, it slows down when it enters the sand but keeps moving straight ahead. If the car approaches the beach at an angle, however, one of its front wheels will be slowed by the sand before the other is, and the car will veer from its original direction. In the same way, a beam of light changes direction when it enters a piece of glass at an angle (Figure 6-1b).
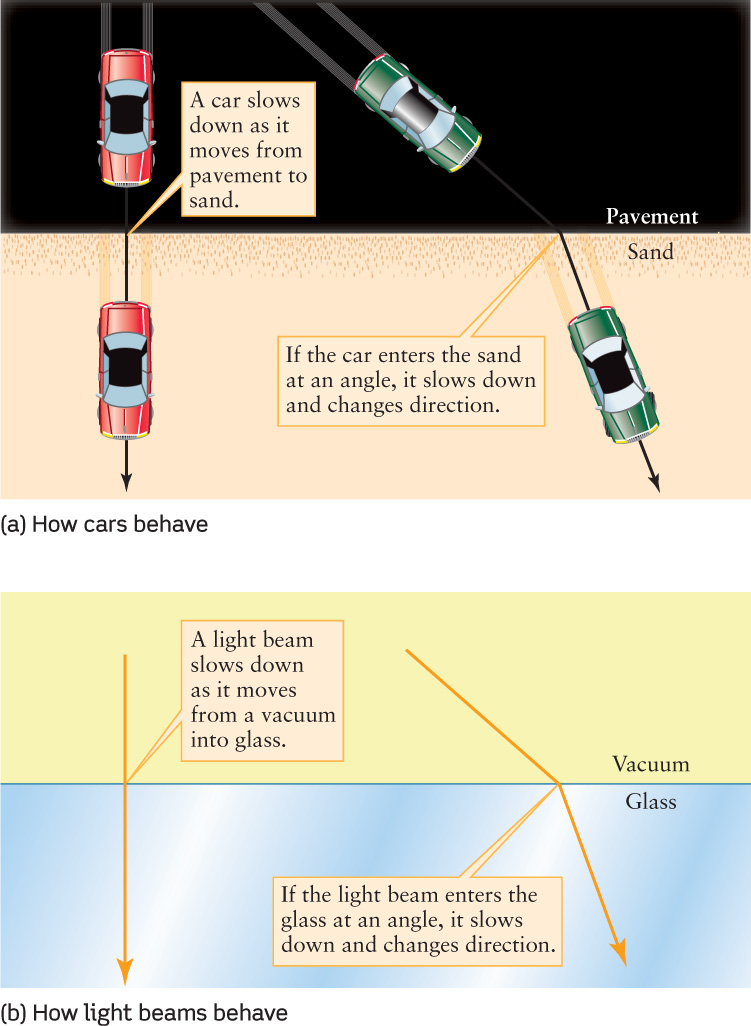
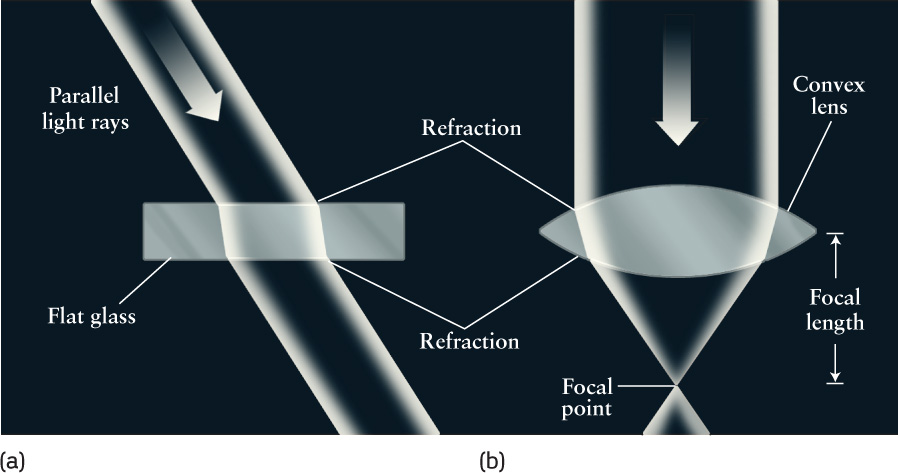
Figure 6-2a shows the refraction of a beam of light passing through a piece of flat glass. As the beam enters the upper surface of the glass, refraction takes place, and the beam is bent to a direction more nearly perpendicular to the surface of the glass. As the beam exits from the glass back into the surrounding air, a second refraction takes place, and the beam bends in the opposite sense. (The amount of bending depends on the speed of light in the glass, so different kinds of glass produce slightly different amounts of refraction.) Because the two surfaces of the glass are parallel, the beam emerges from the glass traveling in the same direction at which it entered.
Lenses and Refracting Telescopes
Something more useful happens if the glass is curved into a convex shape (one that is fatter in the middle than at the edges), like the lens in Figure 6-2b. When a beam of incoming light rays passes through the lens, refraction causes all the outgoing rays to converge at a point called the focus. If the light rays entering the lens are all parallel, the focus occurs at a special point called the focal point. The distance from the lens to the focal point is called the focal length of the lens.
The case of incoming parallel light rays, shown in Figure 6-2b, is not merely a theoretical ideal. The stars are so far away that light rays from them are essentially parallel, as Figure 6-3 shows. Consequently, a lens always focuses light from an astronomical object to the focal point. If the object has a very small angular size, like a distant star, all the light entering the lens from that object converges onto the focal point. The resulting image is just a single bright dot.
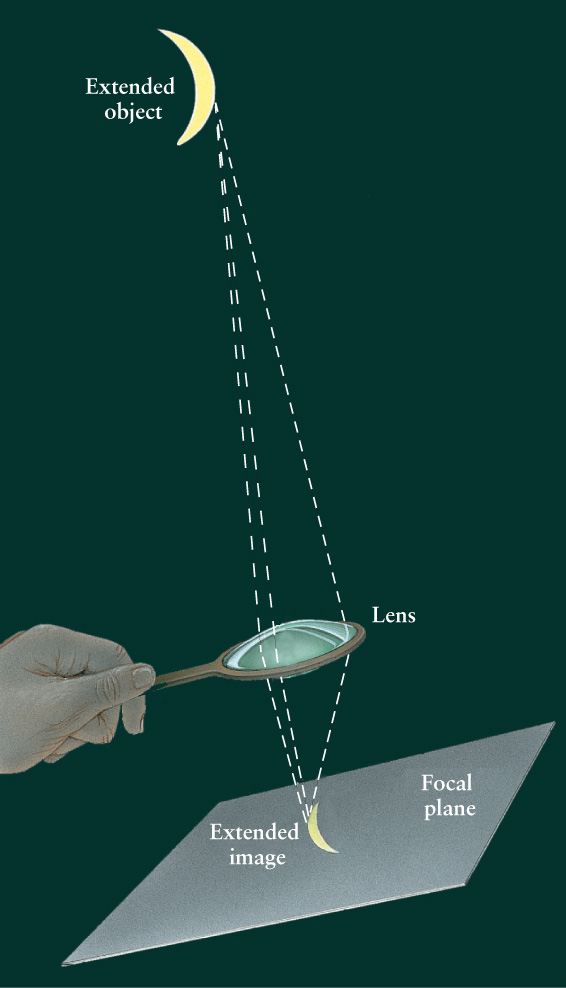

However, if the object is extended—that is, if it has a relatively large angular size, like the Moon or a nearby planet—then light coming from each point on the object is brought to a focus at its own individual point. The result is a clearly focused and extended image that lies in the focal plane of the lens (Figure 6-4), which is a plane that includes the focal point. You can use an ordinary magnifying glass in this way to make an image of the Sun on the ground.
To use a lens to make a permanent picture of an astronomical object, you would place an electronic detector in the focal plane—the same type of detector used in digital cameras. In fact, an ordinary digital camera works in a very similar way for photographing objects here on Earth. However, many amateur astronomers want to view the image with their eye, not a camera, and so they add a second lens to magnify the image formed in the focal plane. Such an arrangement of two lenses is called a refracting telescope, or refractor (Figure 6-5). The large-diameter, long-focal-length lens at the front of the telescope, called the objective lens, forms the image; the smaller, shorter-focal-length lens at the rear of the telescope, called the eyepiece lens, magnifies the image for the observer.
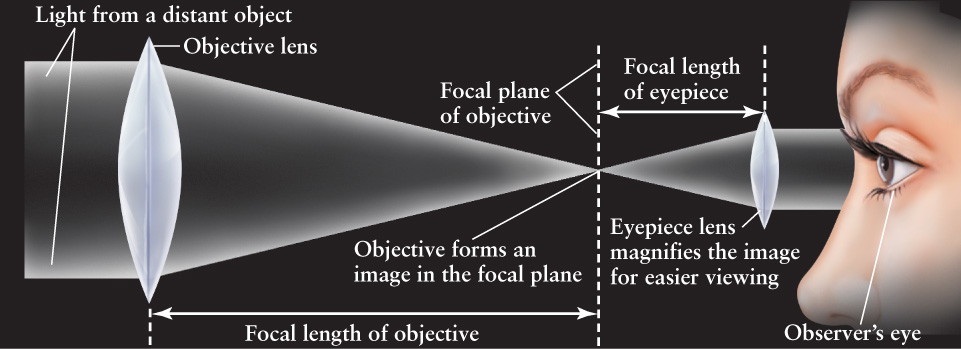
 A Refracting Telescope A refracting telescope consists of a large-diameter objective lens with a long focal length and a small eyepiece lens of short focal length. The eyepiece lens magnifies the image formed by the objective lens in its focal plane (shown as a dashed line). To take a photograph, the eyepiece is removed and an electronic detector is placed in the focal plane.
A Refracting Telescope A refracting telescope consists of a large-diameter objective lens with a long focal length and a small eyepiece lens of short focal length. The eyepiece lens magnifies the image formed by the objective lens in its focal plane (shown as a dashed line). To take a photograph, the eyepiece is removed and an electronic detector is placed in the focal plane.
Light-Gathering Power
In addition to the focal length, the other important dimension of the objective lens of a refractor is its diameter. Compared with a small-diameter lens, a large-diameter lens captures more light, produces brighter images, and allows astronomers to detect fainter objects. (For the same reason, the iris of your eye opens when you go into a darkened room to allow you to see dimly lit objects.)
BOX 6-1 TOOLS OF THE ASTRONOMER’S TRADE
Magnification and Light-Gathering Power
The magnification of a telescope is equal to the focal length of the objective divided by the focal length of the eyepiece. Telescopic eyepieces are usually interchangeable, so the magnification of a telescope can be changed by using eyepieces of different focal lengths.
EXAMPLE: A small refracting telescope has an objective of focal length 120 cm. If the eyepiece has a focal length of 4.0 cm, what is the magnification of the telescope?
Situation: We are given the focal lengths of the telescope’s objective and eyepiece lenses. Our goal is to calculate the magnification provided by this combination of lenses.
Tools: We use the relationship that the magnification equals the focal length of the objective (120 cm) divided by the focal length of the eyepiece (4.0 cm).
Answer: Using this relationship,
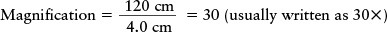
Review: A magnification of 30✕ means that as viewed through this telescope, a large lunar crater that subtends an angle of 1 arcminute to the naked eye will appear to subtend an angle 30 times greater, or 30 arcminutes (one-half of a degree). This magnification makes the details of the crater much easier to see.
If a 2.0-cm-focal-length eyepiece is used instead, the magnification will be (120 cm)/(2.0 cm) = 60×. The shorter the focal length of the eyepiece, the greater the magnification.
The light-gathering power of a telescope depends on the diameter of the objective lens; it does not depend on the focal length. The light-gathering power is proportional to the square of the diameter. As an example, a fully dark adapted human eye has a pupil diameter of about 5 mm. By comparison, a small telescope whose objective lens is 5 cm in diameter has 10 times the diameter and 102 = 100 times the light-gathering power of the eye. (Recall that there are 10 mm in 1 cm.) Hence, this telescope allows you to see objects 100 times fainter than you can see without a telescope.
EXAMPLE: The same relationships apply to reflecting telescopes, discussed in Section 6-2. Each of the two Keck telescopes on Mauna Kea in Hawaii (discussed in Section 6-3; see Figure 6-16) uses a concave mirror 10 m in diameter to bring starlight to a focus. How many times greater is the light-gathering power of either Keck telescope compared to that of the human eye?
Situation: We are given the diameters of the pupil of the human eye (5 mm) and of the mirror of either Keck telescope (10 m). Our goal is to compare the light-gathering powers of these two optical instruments.
Tools: We use the relationship that light-gathering power is proportional to the square of the diameter of the area that gathers light. Hence, the ratio of the light-gathering powers is equal to the square of the ratio of the diameters.
Answer: We first calculate the ratio of the diameter of the Keck mirror to the diameter of the pupil. To determine this ratio, we must first express both diameters in the same units. Because there are 1000 mm in 1 meter, the diameter of the Keck mirror can be expressed as
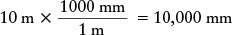
Thus, the light-gathering power of either of the Keck telescopes is greater than that of the human eye by a factor of
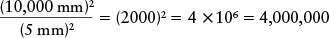
Review: Either Keck telescope can gather 4 million times as much light as a human eye. When it comes to light-gathering power, the bigger the telescope, the better!
The light-gathering power of a telescope is directly proportional to the area of the objective lens, which in turn is proportional to the square of the lens diameter (Figure 6-6). Thus, if you double the diameter of the lens, the light-gathering power increases by a factor of 22 = 2 × 2 = 4. Box 6-1 describes how to compare the light-gathering power of different telescopes.
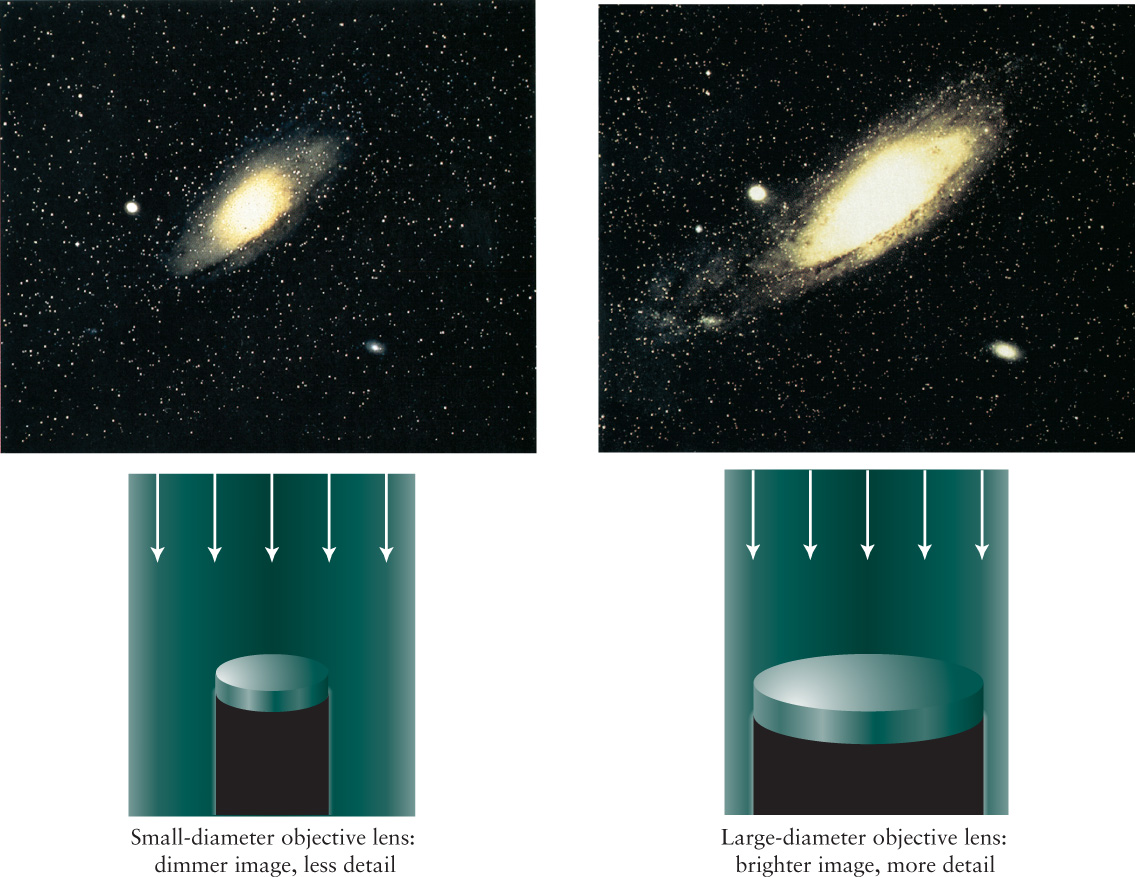
Light-Gathering Power These two photographs of the galaxy M31 in Andromeda were taken using the same exposure time and at the same magnification, but with two different telescopes with objective lenses of different diameters. The right-hand photograph is brighter and shows more detail because it was made using the large-diameter lens, which intercepts more starlight than a small-diameter lens. This same principle applies to telescopes that use curved mirrors rather than lenses to collect light (see Section 6-2).
Because light-gathering power is so important for seeing faint objects, the lens diameter is almost always given when describing a telescope. For example, the Lick telescope on Mount Hamilton in California is a 90-cm refractor, which means that it is a refracting telescope whose objective lens is 90 cm in diameter. By comparison, Galileo’s telescope of 1610 was a 3-cm refractor. The Lick telescope has an objective lens 30 times larger in diameter, and so has 302 or 30 × 30 = 900 times the light-gathering power of Galileo’s instrument.
CONCEPT CHECK 6-1
If someone says they are using an 8-inch telescope, which dimension of the telescope—length or tube diameter—are they most likely referring to?
The diameter, because it is the width of the opening that determines how much light can be captured by the telescope.
CONCEPT CHECK 6-2
If a thick lens is able to bend light more than a thin lens, which lens has a greater focal length?
The thin lens bends light less, so, according to Figure 6-5, it must focus light at a more distant location. Thus, the thinner lens has the greater focal length.
Magnification
In addition to their light-gathering power, telescopes are useful because they magnify distant objects. As an example, the angular diameter of the Moon as viewed with the naked eye is about 0.5°. But when Galileo viewed the Moon through his telescope, its apparent angular diameter was 10°, large enough so that he could identify craters and mountain ranges. The magnification, or magnifying power, of a telescope is the ratio of an object’s angular diameter seen through the telescope to its naked-eye angular diameter. Thus, the magnification of Galileo’s telescope was 10°/0.5° = 20 times, usually written as 20×.
The magnification of a refracting telescope depends on the focal lengths of both of its lenses:
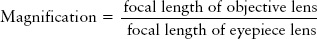
This formula shows that using a long-focal-length objective lens with a short-focal-length eyepiece gives a large magnification. Box 6-1 illustrates how this formula is used.
CAUTION!
Many people think that the primary purpose of a telescope is to magnify images. But in fact magnification is not the most important aspect of a telescope. The reason is that there is a limit to how sharp any astronomical image can be, due either to the blurring caused by Earth’s atmosphere or to fundamental limitations imposed by the nature of light itself. (We will describe these effects in more detail in Section 6-3.) Magnifying a blurred image may make it look bigger but will not make it any clearer. Thus, beyond a certain point, there is nothing to be gained by further magnification. Astronomers place more priority on the light-gathering power of a telescope than in its magnification. Greater light-gathering power means brighter images, which makes it easier to see faint details.
Disadvantages of Refracting Telescopes
If you were to build a telescope like that in Figure 6-5 using only the instructions given so far, you would probably be disappointed with the results. The problem is that a lens bends different colors of light through different angles, just as a prism does (recall Figure 5-3). As a result, different colors do not focus at the same point, and stars viewed through a telescope that uses a simple lens are surrounded by fuzzy, rainbow-colored halos. Figure 6-7a shows this optical defect, called chromatic aberration.
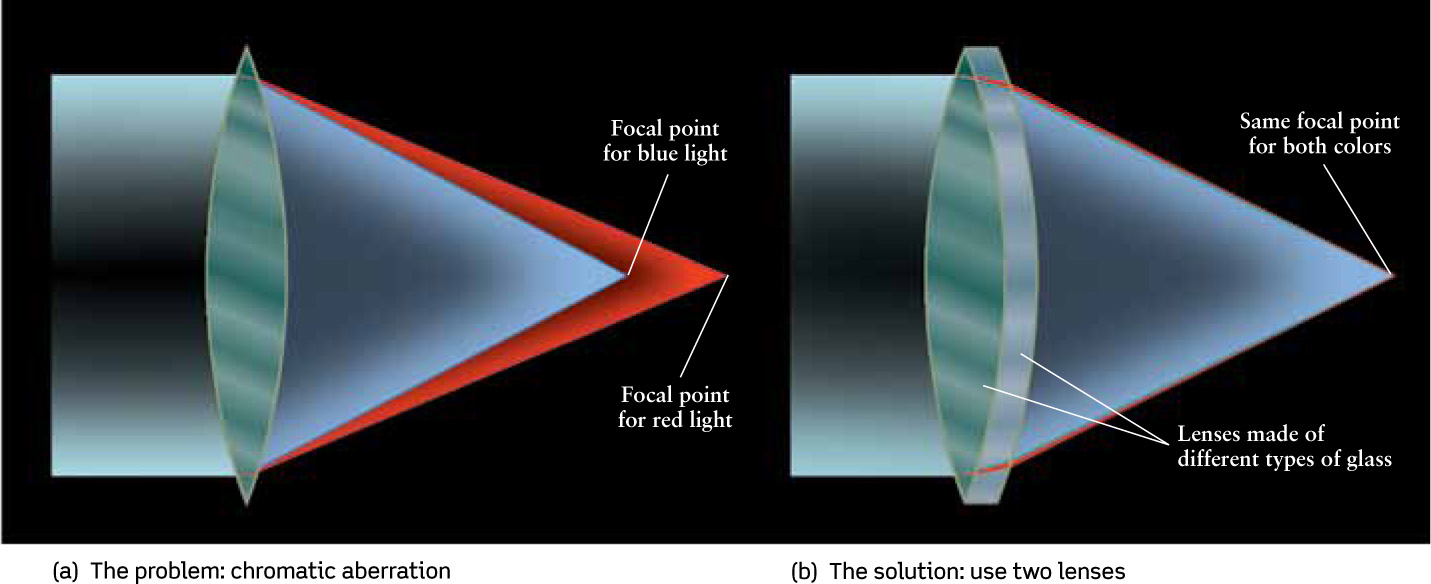
One way to correct for chromatic aberration is to use an objective lens that is not just a single piece of glass. Different types of glass can be manufactured by adding small amounts of chemicals to the glass when it is molten. Because of the different properties of these added chemicals, the speed of light varies slightly from one kind of glass to another, and the refractive properties vary as well. If a thin lens is mounted just behind the main objective lens of a telescope, as shown in Figure 6-7b, and if the telescope designer carefully chooses two different kinds of glass for these two lenses, different colors of light can be brought to a focus at the same point.
Chromatic aberration is only the most severe of a host of optical problems that must be solved in designing a high-quality refracting telescope. Master opticians of the nineteenth century devoted their careers to solving these problems, and several magnificent refractors were constructed in the late 1800s (Figure 6-8).

A Large Refracting Telescope (a) This giant refractor, built in 1897, is housed at Yerkes Observatory near Chicago. The telescope tube is 19.5 m (64 ft) long; it has to be this long because the focal length of the objective is just under 19.5 m (see Figure 6-5). As Earth rotates, the motor drive rotates the telescope in the opposite direction in order to keep the object being studied within the telescope’s field of view. (b) This historical photograph shows the astronomer George van Biesbrock with the objective lens of the Yerkes refractor. This lens, the largest refracting lens still in use, is 102 cm (40 in.) in diameter.
Unfortunately, there are several negative aspects of refractors that even the finest optician cannot overcome:
- Because faint light must readily pass through the objective lens, the glass from which the lens is made must be totally free of defects, such as the bubbles that frequently form when molten glass is poured into a mold. Such defect-free glass is extremely expensive.
- Glass is opaque to certain kinds of light. Ultraviolet light is absorbed almost completely, and even visible light is dimmed substantially as it passes through the thick slab of glass that makes up the objective lens.
- It is impossible to produce a large lens that is entirely free of chromatic aberration.
- Because a lens can be supported only around its edges, a large lens tends to sag and distort under its own weight as it tracks objects through the night. This distortion has negative effects on the image clarity.
For these reasons and more, few major refractors have been built since the beginning of the twentieth century. Instead, astronomers have avoided all of the limitations of refractors by building telescopes that use mirrors instead of lenses to form images.
CONCEPT CHECK 6-3
How do the eyepieces with the largest focal length affect a telescope’s overall magnification?
The larger the eyepiece focal length, the smaller the magnification.