6-3 Telescope images are degraded by the blurring effects of the atmosphere and by light pollution

Figure 6-15: R I V U X G
Angular Resolution The angular resolution of a telescope indicates the sharpness of the telescope’s images. (a) This telescope view shows two sources of light whose angular separation is greater than the angular resolution. (b) The light sources have been moved together so that their angular separation is equal to the angular resolution. If the sources were moved any closer together, the telescope image would show them as a single source.

(Courtesy of John D. Monnier)

In addition to providing a brighter image, a large telescope also helps achieve a second major goal: It produces star images that are sharp and crisp. A quantity called angular resolution gauges how well fine details can be seen. Poor angular resolution causes star images to be fuzzy and blurred together.

To determine the angular resolution of a telescope, pick out two adjacent stars whose separate images are just barely discernible (Figure 6-15). The angle θ (the Greek letter theta) between these stars is the telescope’s angular resolution; the smaller that angle, the finer the details that can be seen and the sharper the image.

When you are asked to read the letters on an eye chart, what’s being measured is the angular resolution of your eye. If you have 20/20 vision, the angular resolution θ of your eye is about 1 arcminute, or 60 arcseconds. (You may want to review the definitions of angles and their units in Section 1-5.) Hence, with the naked eye it is impossible to distinguish two stars less than 1 arcminute apart or to see details on the Moon with an angular size smaller than this. All the planets have angular sizes (as seen from Earth) of 1 arcminute or less, which is why they appear as featureless points of light to the naked eye.

Limits to Angular Resolution

One factor limiting angular resolution is diffraction, which is the tendency of light waves to spread out when they are confined to a small area like the lens or mirror of a telescope. (A rough analogy is the way water exiting a garden hose sprays out in a wider angle when you cover part of the end of the hose with your thumb.) As a result of diffraction, a narrow beam of light tends to spread out within a telescope’s optics, thus blurring the image. If diffraction were the only limit, the angular resolution of a telescope would be given by the formula

Diffraction-limited angular resolution

For a given wavelength of light, using a telescope with an objective of larger diameter D reduces the amount of diffraction and makes the angular resolution θ smaller (and hence better). For example, with red light with wavelength 640 nm, or 6.4 × 10⁻⁷ m, the diffraction-limited resolution of an 8-meter telescope (see Figure 6-15) would be

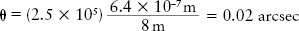
In practice, however, ordinary optical telescopes cannot achieve such fine angular resolution. The problem is that turbulence in the air causes star images to jiggle around and twinkle. Even through the largest telescopes, a star still looks like a tiny blob rather than a pinpoint of light. A measure of the limit that atmospheric turbulence places on a telescope’s resolution is called the seeing disk. This disk is the angular diameter of a star’s image broadened by turbulence. The size of the seeing disk varies from one observatory site to another and from one night to another. At the observatories on Kitt Peak in Arizona and Cerro Tololo in Chile, the seeing disk is typically around 1 arcsec. Some of the very best conditions in the world can be found at the observatories atop Mauna Kea in Hawaii, where the seeing disk is often as small as 0.5 arcsec. These great conditions are one reason why so many telescopes have been built there (Figure 6-16).

Figure 6-16: R I V U X G
The Telescopes of Mauna Kea The summit of Mauna Kea—an extinct Hawaiian volcano that reaches more than 4100 m (13,400 ft) above the waters of the Pacific—has nighttime skies that are unusually clear, still, and dark. To take advantage of these superb viewing conditions, Mauna Kea has become the home of many powerful telescopes.

(AP Photo/University of Hawaii Institute of Astronomy, Richard Wainscoat)

Active Optics and Adaptive Optics

In many cases the angular resolution of a telescope is even worse than the limit imposed by the seeing disk. This occurs if the objective mirror deforms even slightly due to variations in air temperature or slight gravitational sagging of the telescope mount. To combat this, many large telescopes are equipped with an active optics system. Such a system slowly adjusts the mirror shape every few seconds to help keep the telescope in optimum focus and properly aimed at its target. These adjustments can be determined once during a testing phase for each orientation of the telescope and applied for all future observations. However, the adjustments discussed next are more challenging because they change rapidly throughout each observation.

Changing the mirror shape is also at the heart of a more refined technique called adaptive optics. The goal of this technique is to compensate for atmospheric turbulence, so that the angular resolution can be smaller than the size of the seeing disk and can even approach the theoretical limit set by diffraction. Turbulence causes the image of a star to “dance” around erratically. While this turbulence produces twinkling stars seen with the naked eye, it produces blurry images in large telescopes. In an adaptive optics system, sensors monitor this dancing motion 10 to 100 times per second, and a powerful computer rapidly calculates the mirror shape needed to compensate. Fast-acting mechanical devices called actuators then deform the mirror accordingly, to produce a sharp, focused image. In some adaptive optics systems, the actuators deform a small secondary mirror rather than the large objective mirror.

One difficulty with adaptive optics is that a fairly bright star must be in or near the field of the telescope’s view to serve as a “calibration target” for the sensors that track atmospheric turbulence. This is seldom the case, since the field of view of most telescopes is rather narrow, lowering the chances of viewing a sufficiently bright star. With no lack of creative problem-solving, astronomers get around this limitation by shining a laser beam toward a spot in the sky near the object to be observed (Figure 6-17). The laser beam causes atoms in Earth’s upper atmosphere to glow, making an artificial “star.” The light that comes down to Earth from this “star” travels through the same part of our atmosphere as the light from the object being observed, so its image in the telescope will “dance” around in the same erratic way as the image of a real star. By observing how the changing atmosphere distorts the artificial star, computers apply opposing adjustments to cancel the atmosphere’s effects on the real star.

Figure 6-17: R I V U X G
Creating an Artificial “Star” A laser beam shines upward from Yepun, an 8.2-meter telescope at the European Southern Observatory in the Atacama Desert of Chile. (Figure 6-14a shows the objective mirror for this telescope.) The beam strikes sodium atoms that lie about 90 km (56 miles) above Earth’s surface, causing them to glow and make an artificial “star.” Tracking the twinkling of this “star” makes it possible to undo the effects of atmospheric turbulence on telescope images.

(European Southern Observatory)

Figure 6-18 shows the dramatic improvement in angular resolution possible with adaptive optics. Images made with adaptive optics are nearly as sharp as if the telescope were in the vacuum of space, where there is no atmospheric distortion whatsoever and the only limit on angular resolution is diffraction. A number of large telescopes are now being used with adaptive optics systems.

Figure 6-18: R I V U X G
Using Adaptive Optics to “Unblur” Telescope Images The two false-color, inset images show the same 1-arcsecond-wide region of the sky at infrared wavelengths as observed with the 10.0-m Keck II telescope on Mauna Kea (see Figure 6-16). Without adaptive optics, it is impossible to distinguish individual stars in this region. With adaptive optics turned on, more than two dozen stars can be distinguished.

(UCLA Galactic Center Group)

Interferometry

Several large observatories are developing a technique called interferometry that promises to further improve the angular resolution of telescopes. The idea is to have two widely separated telescopes observe the same object simultaneously, then use fiber optic cables to “pipe” the light signals from each telescope to a central location where they “interfere” or blend together. This method makes the combined signal sharp and clear. The effective resolution of such a combination of telescopes is equivalent to that of one giant telescope with a diameter equal to the baseline, or distance between the two telescopes. For example, the Keck I and Keck II telescopes atop Mauna Kea (Figure 6-16) are 85 meters apart, so when used as an interferometer the angular resolution is the same as a single 85-meter telescope.

Interferometry has been used for many years with radio telescopes (which we will discuss in Section 6-6), but is still under development with telescopes for visible light or infrared wavelengths. Astronomers are devoting a great deal of effort to this development because the potential rewards are great. For example, the Keck I and II telescopes used together should give an angular resolution as small as 0.005 arcsec, which corresponds to being able to read the bottom row on an eye chart 36 km (22 miles) away!

Light Pollution

Light from city street lamps and from buildings also degrades telescope images. This light pollution illuminates the sky, making it more difficult to see the stars. You can appreciate the problem if you have ever looked at the night sky from a major city. Only a few of the very brightest stars can be seen, as against the thousands that can be seen with the naked eye from in the desert or the mountains. To avoid light pollution, observatories are built in remote locations far from any city lights.

Unfortunately for astronomers, the expansion of cities has brought light pollution to observatories that in former times had none. As an example, the growth of Tucson, Arizona, has had deleterious effects on observations at the nearby Kitt Peak National Observatory. Efforts have been made to have cities adopt light fixtures that provide safe illumination for their citizens but produce little light pollution. These efforts have met with only mixed success.

One factor over which astronomers have absolutely no control is the weather. Optical telescopes cannot see through clouds, so it is important to build observatories where the weather is usually clear. One advantage of mountaintop observatories such as Mauna Kea is that most clouds form at altitudes below the observatory, giving astronomers a better chance of having clear skies.

In many ways the best location for a telescope is in orbit around Earth, where it is unaffected by weather, light pollution, or atmospheric turbulence. We will discuss orbiting telescopes in Section 6-7.