9.5 Polar Equations; Parametric Equations of Polar Equations; Arc Length of Polar EquationsPrinted Page 670
OBJECTIVES
When you finish this section, you should be able to:
In the previous section, we identified the graphs of polar equations by using geometry or by converting the equation to rectangular coordinates. Since many polar equations cannot be identified in these ways, in this section we graph a polar equation by constructing a table and plotting points. We also show how to find parametric equations for a polar equation. We end the section by finding the length of a curve represented by polar coordinates.
1 Graph a Polar Equation; Find Parametric EquationsPrinted Page 671
EXAMPLE 1Graphing a Polar Equation (Cardioid); Finding Parametric Equations
(a) Graph the polar equation \(r=1-\sin \theta,\;0\leq \theta\leq 2\pi.\)
(b) Find parametric equations for \(r=1-\sin \theta.\)
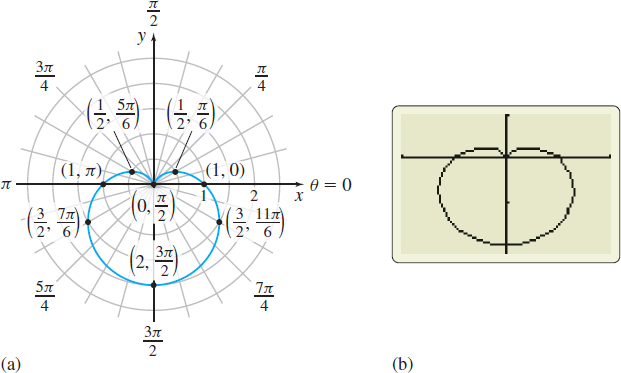
Solution (a) The polar equation \(r=1-\sin \theta\) contains \(\sin \theta\), which has the period \(2\pi .\) We construct Table 2 using common values of \(\theta\) that range from \(0\) to \(2\pi ,\) plot the points \(( r,\theta )\), and trace out the graph, beginning at the point \((1,0)\) and ending at the point \(( 1, \ 2\pi )\), as shown in Figure 43(a). Figure 43(b) shows the graph using technology.
| \(\theta\) | \(r=1-\sin \theta\) | \(( r,\theta )\) |
|---|---|---|
| \(0\) | \(1-0=1\) | \(( 1,0)\) |
| \(\dfrac{\pi }{6}\) | \(1-\dfrac{1}{2}=\dfrac{1}{2}\) | \(\left(\dfrac{1}{2},\dfrac{\pi }{6}\right)\) |
| \(\dfrac{\pi }{2}\) | \(1-1=0\) | \(\left( 0,\dfrac{\pi }{2}\right)\) |
| \(\dfrac{5\pi }{6}\) | \(1-\dfrac{1}{2}=\dfrac{1}{2}\) | \(\left( \dfrac{1}{2},\dfrac{5\pi }{6}\right)\) |
| \(\pi\) | \(1-0=1\) | \(\left( 1, \ \pi \right)\) |
| \(\dfrac{7\pi }{6}\) | \(1-\left( -\dfrac{1}{2}\right) =\dfrac{3}{2}\) | \(\left( \dfrac{3}{2},\dfrac{7\pi }{6}\right)\) |
| \(\dfrac{3\pi }{2}\) | \(1-\left( -1\right) =2\) | \(\left( 2,\dfrac{3\pi }{2}\right)\) |
| \(\dfrac{11\pi }{6}\) | \(1-\left( -\dfrac{1}{2}\right) =\dfrac{3}{2}\) | \(\left( \dfrac{3}{2},\dfrac{11\pi }{6}\right)\) |
| \(2\pi\) | \(1-0=1\) | \(( 1, \ 2\pi )\) |
NOTE
Graphs of polar equations of the form \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \begin{array}{rcl@{\qquad}crcl} r&=&a(1+\cos \theta ) & r=a(1+\sin \theta )\\ r&=&a(1-\cos \theta ) & r=a(1-\sin \theta ) \end{array} }} \]
where \(a>0,\) are called cardioids. A cardioid contains the pole and is heart-shaped (giving the curve its name).
(b) We obtain parametric equations for \(r=1-\sin \theta\) by using the conversion formulas \(x=r \ \cos \theta\) and \(y=r \ \sin\theta\): \[ x=r \ \cos \theta =( 1-\sin \theta ) \ \cos \theta \qquad y=r \ \sin \theta =( 1-\sin \theta ) \ \sin \theta \]
Here, \(\theta\) is the parameter, and if \(0\leq \theta \leq 2\pi ,\) then the graph is traced out exactly once in the counterclockwise direction.
NOW WORK
NOTE
Limaçon (pronounced “leema sown”) is a French word for “snail.”
EXAMPLE 2Graphing a Polar Equation (Limaçon Without an Inner Loop); Finding Parametric Equations
(a) Graph the polar equation \(r=3+2 \ \cos \theta,\;0\leq \theta\leq 2\pi.\)
(b) Find parametric equations for \(r=3+2 \ \cos \theta\).
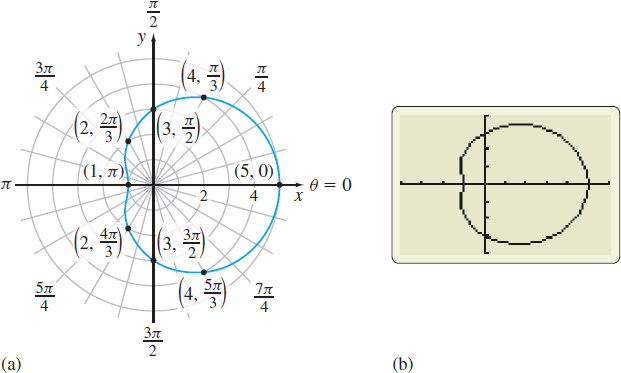
Solution (a) The polar equation \(r=3+2 \ \cos \theta \) contains \(\cos \theta\), which has the period \(2\pi .\) We construct Table 3 using common values of \(\theta \) that range from \(0\) to \(2\pi ,\) plot the points \((r,\theta ) \), and trace out the graph, beginning at the point \((5,0) \) and ending at the point \(( 5, \ 2\pi ) \), as shown in Figure 44(a). Figure 44(b) shows the graph using technology.
672
| \(\theta\) | \(r=3+2 \ \cos \theta\) | \(( r,\theta )\) |
|---|---|---|
| \(0\) | \(3+2(1) =5\) | \(( 5,0)\) |
| \(\dfrac{\pi }{3}\) | \(3+2\left( \dfrac{1}{2}\right) =4\) | \(\left( 4,\dfrac{\pi }{3}\right)\) |
| \(\dfrac{\pi }{2}\) | \(3+2\left( 0\right) =3\) | \(\left( 3,\dfrac{\pi }{2}\right)\) |
| \(\dfrac{2\pi }{3}\) | \(3+2\left( -\dfrac{1}{2}\right) =2\) | \(\left( 2,\dfrac{2\pi }{3}\right)\) |
| \(\pi\) | \(3+2\left( -1\right) =1\) | \(( 1, \ \pi )\) |
| \(\dfrac{4\pi }{3}\) | \(3+2\left( -\dfrac{1}{2}\right) =2\) | \(\left( 2,\dfrac{4\pi }{3}\right)\) |
| \(\dfrac{3\pi }{2}\) | \(3+2\left( 0\right) =3\) | \(\left( 3,\dfrac{3\pi }{2}\right)\) |
| \(\dfrac{5\pi }{3}\) | \(3+2\left( \dfrac{1}{2}\right) =4\) | \(\left( 4,\dfrac{5\pi }{3}\right)\) |
| \(2\pi\) | \(3+2( 1) =5\) | \(( 5, \ 2\pi )\) |
NOTE
Graphs of polar equations of the form \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \begin{array}{rcl@{\qquad}crcl} r&=&a+b \ \cos \theta & r=a+b \ \sin \theta\\ r&=&a-b \ \cos \theta & r=a-b \ \sin \theta \end{array} }} \]
where \(a> b > 0\), are called limaçons without an inner loop. A limaçons on without an inner loop does not pass through the pole.
(b) We obtain parametric equations for \(r=3+2 \ \cos \theta \) by using the conversion formulas \(x=r \ \cos \theta\) and \(y=r \ \sin \theta\): \[ x=r \ \cos \theta = ( 3+2 \ \cos \theta ) \ \cos \theta \qquad y=r \ \sin \theta =( 3+2 \ \cos \theta ) \ \sin \theta \]
Here, \(\theta\) is the parameter, and if \(0\leq \theta \leq 2\pi ,\) then the graph is traced out exactly once in the counterclockwise direction.
NOW WORK
EXAMPLE 3Graphing a Polar Equation (Limaçon with an Inner Loop); Finding Parametric Equations
(a) Graph the polar equation \(r=1+2 \ \cos \theta,\;0\leq \theta\leq 2\pi.\)
(b) Find parametric equations for \(r=1+2 \ \cos \theta \).
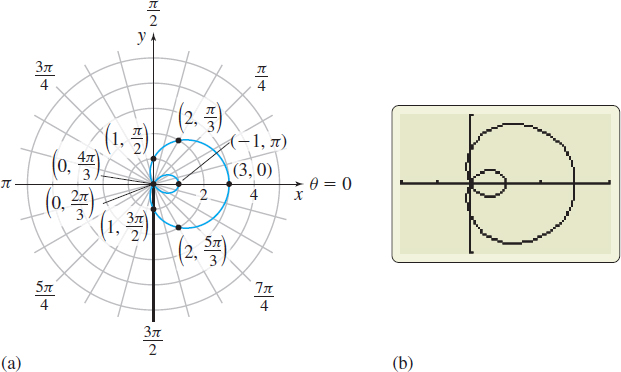
Solution (a) The polar equation \(r=1+2 \ \cos \theta\) contains \(\cos \theta\), which has the period \(2\pi .\) We construct Table 4 using common values of \(\theta \) that range from \(0\) to \(2\pi ,\) plot the points \(( r,\theta )\), and trace out the graph, beginning at the point \(\left(3,0\right)\) and ending at the point \(( 3, \ 2\pi )\), as shown in Figure 45(a). Figure 45(b) shows the graph using technology.
| \(\theta\) | \(r=1+2 \ \cos \theta\) | \(( r,\theta )\) |
|---|---|---|
| \(0\) | \(1+2(1) =3\) | \(( 3,0)\) |
| \(\dfrac{\pi }{3}\) | \(1+2\left( \dfrac{1}{2}\right) =2\) | \(\left( 2,\dfrac{\pi }{3}\right)\) |
| \(\dfrac{\pi }{2}\) | \(1+2\left( 0\right) =1\) | \(\left( 1,\dfrac{\pi }{2}\right)\) |
| \(\dfrac{2\pi }{3}\) | \(1+2\left( -\dfrac{1}{2}\right) =0\) | \(\left( 0,\dfrac{2\pi }{3}\right)\) |
| \(\pi\) | \(1+2( -1) =-1\) | \(\left( -1, \ \pi \right)\) |
| \(\dfrac{4\pi }{3}\) | \(1+2\left( -\dfrac{1}{2}\right) =0\) | \(\left( 0,\dfrac{4\pi }{3}\right)\) |
| \(\dfrac{3\pi }{2}\) | \(1+2\left( 0\right) =1\) | \(\left( 1,\dfrac{3\pi }{2}\right)\) |
| \(\dfrac{5\pi }{3}\) | \(1+2\left( \dfrac{1}{2}\right) =2\) | \(\left( 2,\dfrac{5\pi }{3}\right)\) |
| \(2\pi\) | \(1+2( 1) =3\) | \(( 3, \ 2\pi )\) |
673
NOTE
Graphs of polar equations of the form \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \begin{array}{rcl@{\qquad}crcl} r&=&a+b \ \cos \theta & r=a+b \ \sin \theta\\ r&=&a-b \ \cos \theta & r=a-b \ \sin \theta \end{array} }} \]
where \(0\lt a\lt b,\) are called limaçons with an inner loop. A limaçon with an inner loop passes through the pole twice.
(b) We obtain parametric equations for \(r=1+2 \ \cos \theta\) by using the conversion formulas \(x=r \ \cos \theta\) and \(y=r \ \sin \theta\): \[ x=r \ \cos \theta =( 1+2 \ \cos \theta ) \ \cos \theta \qquad y=r \ \sin \theta =( 1+2 \ \cos \theta ) \ \sin \theta \]
Here, \(\theta\) is the parameter, and if \(0\leq \theta \leq 2\pi ,\) then the graph is traced out exactly once in the counterclockwise direction.
NOW WORK
EXAMPLE 4Graphing a Polar Equation (Rose); Finding Parametric Equations
(a) Graph the polar equation \(r=2 \ \cos ( 2\theta ) ,\) \(0\leq \theta \leq 2\pi\).
(b) Find parametric equations for \(r=2 \ \cos ( 2\theta )\).
NOTE
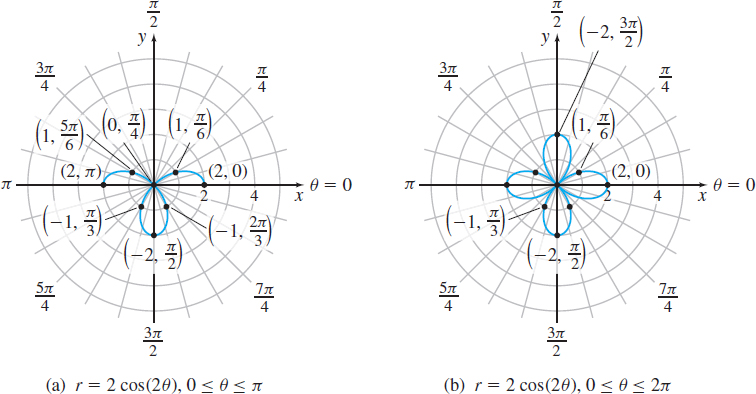
Graphs of polar equations of the form \(r=a \ \cos (n\theta )\) or \(r =a \ \sin ( n\theta ),\;a>0,\;n\) an integer, are called roses. If \(n\) is an even integer, the rose has \(2n\) petals and passes through the pole \(4n\) times. If \(n\) is an odd integer, the rose has \(n\) petals and passes through the pole \(2n\) times.
Solution (a) The polar equation \(r=2 \ \cos ( 2\theta )\) contains \(\cos ( 2\theta )\), which has the period \(\pi\). So, we construct Table 5 using common values of \(\theta\) that range from \(0\) to \(2\pi\), noting that the values for \(\pi \leq \theta \leq 2\pi\) repeat the values for \(0\leq \theta \leq \pi .\) Then we plot the points \(( r,\theta)\) and trace out the graph. Figure 46(a) on page 674 shows the graph from the point \(( 2,0)\) to the point \(( 2, \ \pi).\) Figure 46(b) completes the graph from the point \(( 2, \ \pi)\) to the point \(( 2, \ 2\pi )\).
| \(\theta\) | \(r=2 \ \cos ( 2\theta )\) | \(( r,\theta )\) |
|---|---|---|
| \(0\) | \(2(1) =2\) | \(( 2,0)\) |
| \(\dfrac{\pi }{6}\) | \(2\left( \dfrac{1}{2}\right) =1\) | \(\left( 1,\dfrac{\pi }{6}\right)\) |
| \(\dfrac{\pi }{4}\) | \(2\left( 0\right) =0\) | \(\left( 0,\dfrac{\pi }{4}\right)\) |
| \(\dfrac{\pi }{3}\) | \(2\left( -\dfrac{1}{2}\right) =-1\) | \(\left( -1,\dfrac{\pi }{3}\right)\) |
| \(\dfrac{\pi }{2}\) | \(2\left( -1\right) =-2\) | \(\left(-2,\dfrac{\pi }{2}\right)\) |
| \(\dfrac{2\pi }{3}\) | \(2\left( -\dfrac{1}{2}\right) =-1\) | \(\left( -1,\dfrac{2\pi }{3}\right)\) |
| \(\dfrac{3\pi }{4}\) | \(2\left( 0\right) =0\) | \(\left( 0,\dfrac{3\pi }{4}\right)\) |
| \(\dfrac{5\pi }{6}\) | \(2\left( \dfrac{1}{2}\right) =1\) | \(\left( 1,\dfrac{5\pi }{6}\right)\) |
| \(\pi\) | \(2(1) =2\) | \(( 2, \ \pi)\) |
| \(\dfrac{7\pi }{6}\) | \(2\left( \dfrac{1}{2}\right) =1\) | \(\left( 1,\dfrac{7\pi }{6}\right)\) |
| \(\dfrac{5\pi }{4}\) | \(2(0) =0\) | \(\left( 0,\dfrac{5\pi }{4}\right)\) |
| \(\dfrac{4\pi }{3}\) | \(2\left( -\dfrac{1}{2}\right) =-1\) | \(\left( -1,\dfrac{4\pi }{3}\right)\) |
| \(\dfrac{3\pi }{2}\) | \(2\left( -1\right) =-2\) | \(\left( -2,\dfrac{3\pi }{2}\right)\) |
| \(\dfrac{5\pi }{3}\) | \(2\left( -\dfrac{1}{2}\right) =-1\) | \(\left( -1,\dfrac{5\pi }{3}\right)\) |
| \(\dfrac{7\pi }{4}\) | \(2\left(0\right) =0\) | \(\left( 0,\dfrac{7\pi }{4}\right)\) |
| \(\dfrac{11\pi }{6}\) | \(2\left( \dfrac{1}{2}\right) =1\) | \(\left( 1,\dfrac{11\pi }{6}\right)\) |
| \( 2\pi\) | \(2(1) =2\) | \(( 2, \ 2\pi )\) |
(b) Parametric equations for \(r=2 \ \cos ( 2\theta )\): \begin{equation*} x=r \ \cos \theta =2 \ \cos ( 2\theta ) \ \cos \theta \qquad y=r \ \sin \theta =2 \ \cos ( 2\theta ) \ \sin \theta \end{equation*}
where \(\theta\) is the parameter, and if \(0\leq \theta \leq 2\pi ,\) then the graph is traced out exactly once in the counterclockwise direction.
NOW WORK
674
EXAMPLE 5Graphing a Polar Equation (Spiral); Finding Parametric Equations
(a) Graph the equation \(r=e^{\theta /5}\).
NOTE
Graphs of polar equations of the form \(r=e^{\theta /a},\) \(a>0,\) are called logarithmic spirals, since the equation can be written as \(\theta =a \ln r\). A logarithmic spiral spirals infinitely both toward the pole and away from it.
(b) Find parametric equations for \(r=e^{\theta /5}\).
Solution The polar equation \(r=e^{\theta /5}\) lacks the symmetry you may have observed in the previous examples. Since there is no number \(\theta\) for which \(r=0\), the graph does not contain the pole. Also observe that:
- \(r\) is positive for all \(\theta\).
- \(r\) increases as \(\theta\) increases.
- \(r\rightarrow 0\) as \(\theta \rightarrow -\infty\).
- \(r\rightarrow \infty\) as \(\theta \rightarrow \infty \).
We use a calculator to obtain Table 6. Figure 47(a) shows part of the graph \(r=e^{\theta /5}.\) Figure 47(b) shows the graph for \(\theta =-\dfrac{3\pi}{2}\) to \(\theta =2\pi\) using technology.
| \(\theta\) | \(r=e^{\theta /5}\) | \(( r,\theta )\) |
|---|---|---|
| \(-\dfrac{3\pi }{2}\) | \(\ 0.39\) | \(\left( 0.39,-\dfrac{3\pi }{2}\right)\) |
| \(-\pi\) | \(\ 0.53\) | \(( 0.53,-\pi )\) |
| \(-\dfrac{\pi }{2}\) | \(\ 0.73\) | \(\left( 0.73,-\dfrac{\pi }{2}\right)\) |
| \(-\dfrac{\pi }{4}\) | \(\ 0.85\) | \(\left( 0.85,-\dfrac{\pi }{4}\right)\) |
| \(0\) | \(\ 1\) | \(\left( 1,0\right)\) |
| \(\dfrac{\pi }{4}\) | \(\ 1.17\) | \(\left( 1.17,\dfrac{\pi }{4}\right)\) |
| \(\dfrac{\pi }{2}\) | \(\ 1.37\) | \(\left( 1.37,\dfrac{\pi }{2}\right)\) |
| \(\pi\) | \(\ 1.87\) | \(( 1.87, \ \pi )\) |
| \(\dfrac{3\pi }{2}\) | \(\ 2.57\) | \(\left( 2.57,\dfrac{3\pi }{2}\right)\) |
| \(2\pi\) | \(\ 3.51\) | \(( 3.51, \ 2\pi )\) |
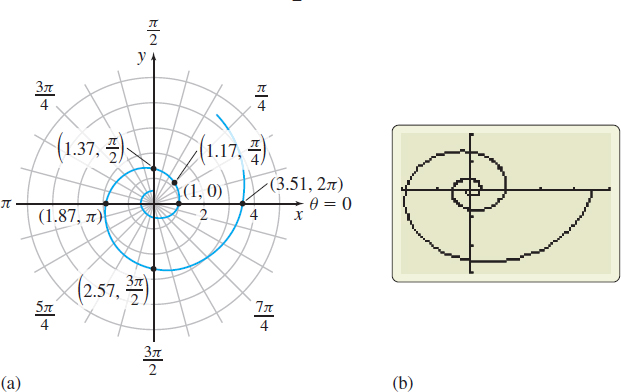
(b) We obtain parametric equations for \(r=e^{\theta /5}\) by using the conversion formulas \(x=r \ \cos \theta\) and \(y=r \ \sin \theta\): \[ x=r \ \cos \theta =e^{\theta /5} \ \cos \theta \qquad y=r \ \sin \theta =e^{\theta /5}\sin \theta \]
where \(\theta\) is the parameter and \(\theta\) is any real number.
| Name | Cardioid | Limaçon without inner loop | Limaçon with inner loop |
|---|---|---|---|
| Polar equations | \(r=a\pm a \ \cos\theta,\;a>0\) | \(r=a\pm b \ \cos\theta,\;0\lt b\lt a\) | \(r=a\pm b \ \cos\theta,\;0\lt a\lt b\) |
| \(r=a\pm a \ \sin\theta,\;a>0\) | \(r=a\pm b \ \sin\theta,\;0\lt b\lt a\) | \(r=a\pm b \ \sin\theta,\;0\lt a\lt b\) | |
| Typical graph | 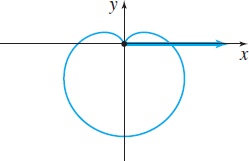
|
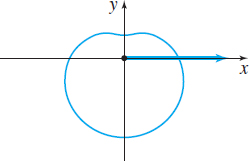
|
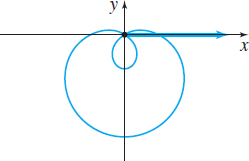
|
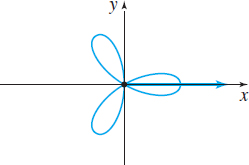
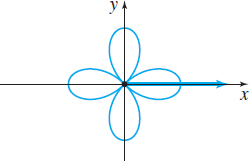
| Name | Lemniscate (See p. 677) | Rose with three petals | Rose with four petals |
|---|---|---|---|
| Polar equations | \(r^2 = a^2 \ \cos (2\theta),\;a>0\) | \(r=a \ \sin(3\theta),\;a>0\) | \(r=a \ \sin(2\theta),\;a>0\) |
| \(r^2 = a^2 \ \sin (2\theta),\;a>0\) | \(r=a \ \cos(3\theta),\;a>0\) | \(r=a \ \cos(2\theta),\;a>0\) | |
| Typical graph | 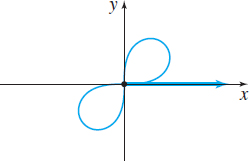
|
|
|
2 Find the Arc Length of a Curve Represented by a Polar EquationPrinted Page 675
675
Suppose a curve \(C\) is represented by the polar equation \(r=f(\theta ),\;\alpha \leq \theta \leq \beta ,\) where both \(f\) and its derivative \(f'( \theta) =\dfrac{dr}{d\theta }\) are continuous on an interval containing \(\alpha \) and \(\beta \). Using \(\theta\) as the parameter, parametric equations for the curve \(C\) are \begin{equation*} x( \theta) =r \ \cos \theta =f (\theta ) \ \cos \theta \qquad y( \theta) =r \ \sin \theta =f(\theta ) \ \sin \theta \end{equation*}
Then \begin{equation*} \frac{dx}{d\theta }=-f(\theta ) \ \sin \theta +f' (\theta ) \ \cos \theta \qquad \frac{dy}{d\theta }=f(\theta ) \ \cos \theta +f' (\theta ) \ \sin \theta \end{equation*}
After simplification, \begin{equation*} \left( \frac{dx}{d\theta }\right) ^{2}+\left( \frac{dy}{d\theta }\right) ^{2}=[ f(\theta )] ^{2}+[ f' ( \theta) ] ^{2}=r^{2}+\left( \dfrac{dr}{d\theta }\right) ^{2}\qquad \color{#0066A7}{{\hbox{\(r=f(\theta)\)}}} \end{equation*}
Since we are using parametric equations, the length \(s\) of \(C\) from \(\theta=\alpha\) to \(\theta =\beta\) is \[ s=\int_{\alpha }^{\beta }\sqrt{\left( \dfrac{dx}{d\theta }\right) ^{2}+\left( \dfrac{dy}{d\theta }\right) ^{2}}\,\,d\theta = \int_{\alpha }^{\beta }\sqrt{r^2 + \left(\dfrac{dr}{d\theta}\right)^2}\,\,d\theta \]
THEOREM Arc Length of the Graph of a Polar Equation
If a curve \(C\) is represented by the polar equation \(r=f(\theta), \alpha \leq \theta \leq \beta\), and if \(f' (\theta )=\dfrac{dr}{d\theta }\) is continuous on an interval containing \(\alpha\) and \(\beta\), then the arc length \(s\) of \(C\) from \(\theta =\alpha\) to \(\theta =\beta\) is \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ s=\int_{\alpha }^{\beta }\sqrt{\,r^{2}+\left( \dfrac{dr}{d\theta }\right) ^{2}}\,d\theta}} \]
676
EXAMPLE 6Finding the Arc Length of a Logarithmic Spiral
Find the arc length \(s\) of the logarithmic spiral represented by \(r=f(\theta)=e^{3\theta }\) from \(\theta = 0\) to \(\theta =2.\)
Solution We use the arc length formula \(s=\int_{\alpha }^{\beta } \sqrt{\,r^{2}+\left( \dfrac{dr}{d\theta }\right) ^{2}}\,d\theta\) with \(r=e^{3\theta }\). Then \(\dfrac{dr}{d\theta }=3e^{3\theta }\) and \begin{eqnarray*} s&=&\int_{0}^{2}\sqrt{(e^{3\theta })^{2}+(3e^{3\theta })^{2}}\,d\theta =\int_{0}^{2}\sqrt{10e^{6\theta }}d\theta =\sqrt{10}\int_{0}^{2}e^{3\theta }\,d\theta\\ &=& \sqrt{10}\left[\dfrac{e^{3\theta}}{3}\right]^2_0 =\frac{\sqrt{10}}{3}(e^{6}-1) \end{eqnarray*}
