3.6 CHEMICAL REACTIONS IN BIOLOGY
Life is possible because molecules in biological systems frequently undergo chemical reactions, enabling organisms to replicate DNA, synthesize RNA and protein molecules, pump small molecules into and out of cells, and use energy in the form of food or light. In this section we discuss the physical principles governing chemical reactions. We review the fundamental laws of thermodynamics and the roles of catalysts in accelerating the rates of reactions between biomolecules. Finally, we describe how energy, in the form of high-
The Mechanism and Speed of Chemical Transformation Define Chemical Reactions
Chemical reactions involve the breakage of covalent bonds and the formation of new bonds. Typically, chemical reactions are written with the reactants, or starting molecules, on the left and the products on the right, connected by an arrow indicating the direction of the reaction. For example, the expression
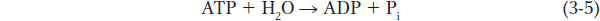
describes a very common reaction in biology: the breakage of a phosphorus–
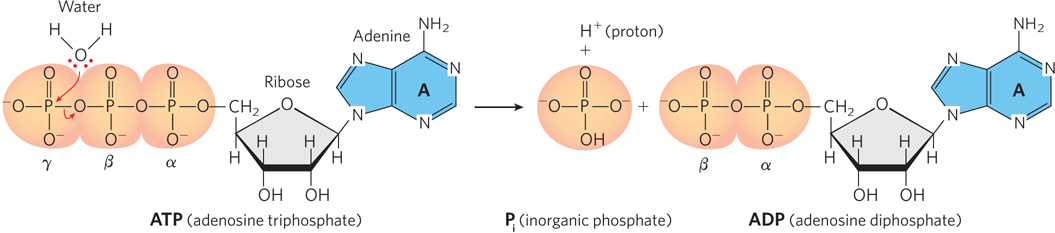
Reactions of this type involve the attack of a nucleophile, a strongly electronegative atom, such as oxygen or nitrogen, on a less electronegative atom, such as phosphorus or carbon. When the nucleophile initiating the reaction is part of a water molecule, as in Figure 3-26, the reaction is known as hydrolysis.
84
Most chemical reactions that take place in biological systems are not spontaneous; if they were, they would be impossible to control, and life as we know it could not exist. Instead, the starting and ending points of chemical reactions are bridged by an energy barrier, called the activation energy, that separates the reactants from the products (Figure 3-27). As reactants come together and bonds are breaking and forming, the reacting species progress through a high-
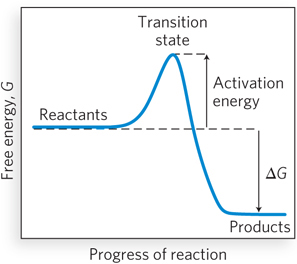
A reaction mechanism is the sequence of individual steps that take place during the conversion of reactants to products. It shows which bonds are breaking and forming and which species are reaction intermediates—substances that form and exist for an extremely short time before being converted to other intermediates or to reaction products. Understanding the mechanisms of chemical reactions that occur in living systems is important in molecular biology because it helps us understand how these reactions are used and controlled during such processes as cell growth and responses to chemical stimuli.
Although it is often difficult to determine reaction mechanisms, understanding the reaction kinetics, the rates at which the reaction proceeds in the forward and reverse directions, can provide important clues. Reaction rates are a function of the concentration of reactants (when the reaction is catalyzed by an enzyme, reactants are called substrates) and their tendency to react. Chemical reactions require collisions between molecules, and collisions occur more frequently when there are more molecules per unit volume. It is important to note that reaction rates also depend on the individual steps that make up the reaction. Usually, one step is slower than the others, and this slowest step, the rate-
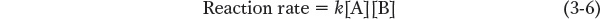
85
where k is a value called the rate constant, a property of the overall reaction that quantitatively describes the tendency to react. A possible mechanism for this reaction might be:
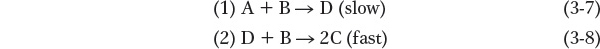
Step 1, the rate-
Many biologically important reactions involve not just two but many individual steps. As we shall see, the identification of so many individual steps can be extremely challenging.
Biological Systems Follow the Laws of Thermodynamics
Living systems demand an almost constant input of energy, and as a result, organisms devote considerable molecular machinery to obtaining and using it. Biology obeys the physical laws of thermodynamics, which are the foundation for understanding energy and its effects on matter. In thermodynamics, a system is defined as a container or organism or other portion of the universe that is under study, and the rest of the universe, outside the system of interest, is called the surroundings.
The first law of thermodynamics states that energy can never be created or destroyed; in other words, the energy of a system is conserved. In a thermodynamic system, all readily occurring (spontaneous) processes take place without the input of additional energy from outside. The first law of thermodynamics cannot predict whether a process is spontaneous, however. For example, heat spontaneously transfers from a warmer object to a cooler one, never the reverse. Yet transfer in either direction is consistent with the first law of thermodynamics, because the total energy of the system remains unchanged in either case. To determine which direction of a process or reaction is spontaneous, we need additional criteria.
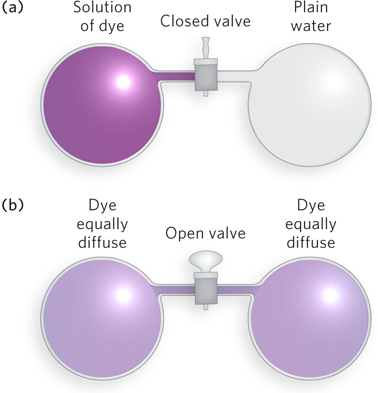
According to the second law of thermodynamics, all spontaneous processes take place with an increase in disorder, or entropy, of the system. Consider, for instance, two vessels of equal volume, one filled with plain water and the other with water containing a dye. When a connecting valve is opened, the dye molecules become randomly but equally distributed between the two vessels (Figure 3-28). The likelihood of all the dye molecules spontaneously remaining in the first vessel, or all the dye molecules moving into the other vessel, is essentially zero, even though the energy of either of these arrangements is no different from that of the evenly distributed molecules. The spontaneity of a process, such as a biochemical reaction, cannot be predicted from knowledge of the system’s entropy change alone.
Every closed system, where no reactants or products can escape, tends toward equilibrium, a state in which the forward and reverse reaction rates are exactly balanced. The approach to equilibrium is accompanied by a transfer of energy from one form to another, such as from potential (stored) energy to kinetic energy. The concept of free energy (G) provides a useful way to express this energy change. Free energy, denoted by the symbol G (for nineteenth-
The tendency of a chemical reaction to proceed to completion can be expressed as an equilibrium constant, which is related to the standard Gibbs free-
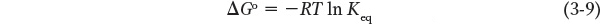
86
where R is the universal gas constant (1.987 cal/mol • K),T is the absolute temperature (298 at 25°C), and ln Keq is the natural logarithm of the equilibrium constant Keq. The standard state (under which Keq is measured) requires that all reactants be present at a concentration of 1 mol/L (1 m). For any compound, the ΔGo of formation ( ) is the change in free energy that accompanies the formation of 1 mol of that substance from its component elements in their standard states (the most stable form of each element at 25°C and 100 kPa (kilopascals) of atmospheric pressure). Because Keq can be measured experimentally, this relationship gives us a way of calculating ΔGo—the thermodynamic constant characteristic of each reaction. When Keq is much greater than 1, ΔGo is large and negative; reactions of this nature tend to go to completion. In contrast, when Keq is much smaller than 1, ΔGo is large and positive; reactions with this property are not spontaneous and require energy to drive them to completion.
) is the change in free energy that accompanies the formation of 1 mol of that substance from its component elements in their standard states (the most stable form of each element at 25°C and 100 kPa (kilopascals) of atmospheric pressure). Because Keq can be measured experimentally, this relationship gives us a way of calculating ΔGo—the thermodynamic constant characteristic of each reaction. When Keq is much greater than 1, ΔGo is large and negative; reactions of this nature tend to go to completion. In contrast, when Keq is much smaller than 1, ΔGo is large and positive; reactions with this property are not spontaneous and require energy to drive them to completion.
Catalysts Increase the Rates of Biological Reactions
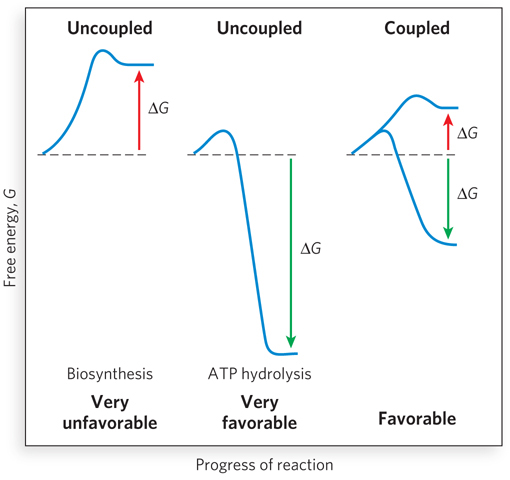
The ΔG of a chemical reaction reflects its equilibrium. However, ΔG, whether positive or negative, bears no relationship to the rate of the reaction. For example, the series of reactions that convert glucose to H2O and CO2 in most cells is thermodynamically favorable, with a net ΔG that is highly negative. However, a large, negative ΔG does not correlate with a fast reaction. A sterile solution of glucose will sit on a laboratory shelf for months with no detectable change. Glucose remains stable because of the substantial activation energy barrier that exists for its reaction. Virtually every chemical reaction in a cell occurs at a significant rate only because of the action of enzymes, which, like all catalysts, are molecules that dramatically increase the rate of specific chemical reactions without being consumed in the process.
Catalysts function by lowering the activation energy for a particular reaction without affecting the reaction equilibrium. Given that a catalyst changes the reaction’s rate but not its equilibrium, it must change the rate of the reverse reaction to the same extent as the rate of the forward reaction. Catalysts can do this because they enable the reaction to proceed by a different mechanism than that of the uncatalyzed reaction. For example, enzymes bind to the transition state of the reactants by providing a molecular surface complementary to its shape and charge. Because of this favorable interaction, binding of an enzyme stabilizes the transition state, reducing the activation energy for the reaction and thus greatly enhancing the reaction rate. Additional contributions to catalysis occur when reacting molecules—
Most cellular enzymes are proteins, though some RNA molecules also have catalytic activity. In general, each enzyme catalyzes a specific reaction, and each reaction in a cell is catalyzed by a different enzyme. Thus, many thousands of enzymes are required in each cell. Because enzymes are exquisitely capable of discriminating between substrates, and because they are subject to various regulatory mechanisms, cells can selectively adjust reaction rates. Such selectivity is critical for the effective control of cellular processes. By enabling specific reactions to occur at particular times and locations within a cell or organism, enzymes determine how chemicals and energy are channeled into biological activities. Enzyme function is described in detail in Chapter 5.
Energy Is Stored and Released by Making and Breaking Phosphodiester Bonds
The formation and breakdown of adenosine triphosphate (ATP) (and in some cases guanosine triphosphate, GTP) links the molecule-
Because the hydrolysis of a phosphodiester bond is exothermic under physiological conditions, energy is released when ATP is hydrolyzed to ADP. In turn, the free energy stored in the phosphodiester bonds of ATP is used to drive biosynthetic reactions of metabolism. Although energy is required for bond breaking in ATP, the products of the reaction (ADP and phosphate) form highly favorable interactions with water. Thus, hydration of the breakdown products of ATP more than makes up for the input energy necessary to break the bond in the first place, resulting in an overall energetically favorable process. Almost as soon as it is formed in concert with a coupled degradative reaction (or by photosynthesis), ATP is consumed by enzymes to provide the energy necessary to propel another reaction to completion. In this way, ATP functions as a transient vehicle of intracellular energy transfer (Highlight 3-2).
ATP consists of an adenosine nucleoside (base + ribose) and three phosphate groups (see Figure 3-26). The phosphate groups, starting with the one directly bonded to ribose, are referred to as the alpha (α), beta (β), and gamma (γ) phosphates, respectively. Like other such high-
87
HIGHLIGHT 3-2 EVOLUTION: ATP: The Critical Molecule of Energy Exchange in All Cells

The universal role of ATP in cellular reactions has led many molecular biologists and chemists to question its origin and the reasons for its emergence as the universal mediator of energy exchange in cells. Experiments performed by Juan Oro, Stanley Miller, and Harold Urey in the 1950s and 1960s showed that adenine bases can be produced by heating concentrated hydrogen cyanide and ammonia, leading to speculation that adenine came into wide biological use in part because it arose very early in the evolution of life. The yields of adenine in the laboratory experiments ranged from ~1% to upward of 20%, depending on the reaction conditions. However, the likelihood of concentrated cyanide and ammonia existing in the environment of early Earth is uncertain. Adenine has been found in meteorites, though, providing evidence that it is produced naturally in space. Some researchers have speculated that various inorganic clays could have helped sequester adenine and foster its reaction with ribose to form adenosine nucleosides (see the How We Know section in Chapter 1). The uncatalyzed phosphorylation of nucleosides to nucleotides (i.e., of adenosine nucleoside to AMP, ADP, and ATP) has been observed under hot, dry experimental conditions. To date, however, such proposed prebiotic reactions have not been found to proceed efficiently. More research is required to determine whether other synthetic conditions could suggest more plausible pathways for prebiotic accumulation of nucleotides.
Note that a single hydrolytic reaction produces one Pi and ADP, and the ADP can be broken down further to yield a second Pi and adenosine monophosphate (AMP). But ATP can also be hydrolyzed to AMP directly, with the release of inorganic diphosphate, or pyrophosphate (PPi). This latter reaction is effectively irreversible in the cellular environment, because enzymes called pyrophosphatases rapidly hydrolyze pyrophosphate into two phosphates. As a result, it would be very difficult to accumulate sufficient concentrations of pyrophosphate in the cell to drive the reaction in the reverse direction. Thus, the hydrolysis of ATP to AMP can be used to render a coupled process effectively irreversible.
For example, DNA and RNA are synthesized from nucleoside triphosphate precursors through a reaction that forms a phosphodiester bond and releases PPi. The required free energy of bond formation comes in part from the concomitant splitting of the high-
In addition to phosphorus–
88
The overall free-
SECTION 3.6 SUMMARY
Chemical reactions involve the breakage of covalent bonds and formation of new bonds. They are written with reactants on the left and products on the right. Half-
headed arrows (  ) indicate that the reaction can proceed in either direction.
) indicate that the reaction can proceed in either direction.The starting and ending points of a chemical reaction are bridged by an activation energy, a barrier that separates reactants from products. As reactants come together and bonds are breaking and forming, the reacting species progress through a high-
energy transition state, at which point decay to substrates or decay to products are equally probable, because it is downhill either way. Reaction rates depend on the individual steps in the reaction. Usually, one step is slower than the others, and this rate-
limiting step governs the overall reaction rate. Chemical reactions obey the laws of thermodynamics. The first law states that energy can never be created or destroyed. The second law states that all spontaneous processes take place with an increase in disorder, or entropy, of the system.
Free energy, G, is energy that can do work. According to the second law of thermodynamics, free energy always decreases (ΔG is negative) in spontaneous reactions that occur without a temperature or pressure change. The tendency of a chemical reaction to proceed to completion is expressed by an equilibrium constant (Keq), which is related to the standard free-
energy change (ΔGo) of the reaction by the expression: ΔGo = −RT ln Keq
Virtually every chemical reaction in a cell occurs at a significant rate only because enzymes dramatically increase the rate of chemical reactions without being consumed in the process.
Breakdown of the phosphodiester bonds between the phosphates of adenosine triphosphate (ATP) by reaction with water (hydrolysis) produces significant free energy, which can be used to change the structure or binding properties of enzymes and thus assist in catalyzing other cellular reactions. Phosphate groups are transferred from ATP to other metabolites or proteins in a coupled reaction, yielding new high-
energy phosphate bonds that can be hydrolyzed to provide the free energy for further reactions.
89
HOW WE KNOW: Single Hydrogen Atoms Are Speed Bumps in Enzyme-Catalyzed Reactions
Cha Y., C.J. Murray, and J.P. Klinman. 1989. Hydrogen tunneling in enzyme reactions. Science 243:1325–
Klinman J.P., and A. Kohen. 2014. Hydrogen tunneling links protein dynamics to enzyme catalysis. Annu. Rev. Biochem. 82:471–

Understanding what limits the rates of biochemical reactions, and how enzymes speed them up, has long fascinated scientists. Thanks to a phenomenon called the kinetic isotope effect, researchers can deduce how single atoms affect reaction rates. Kinetic isotope effects are observed when different isotopes of an atom (such as of hydrogen or carbon), incorporated into a reactant, alter the rate of a chemical reaction. Substituting one isotope for another in a chemical bond that is broken or formed in the rate-
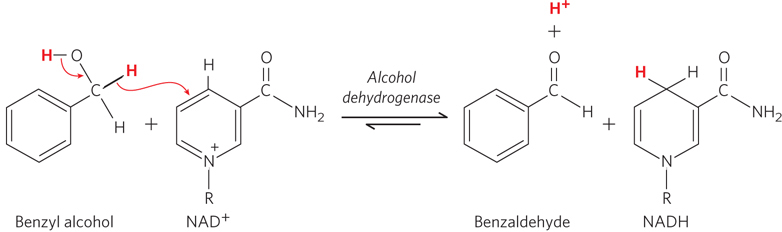
In experiments of this type, the isotope-
These initial findings for alcohol dehydrogenase, and later for additional enzymes, led Klinman and other researchers to conclude that many enzymes enhance chemical reaction rates by speeding up the movement of hydrogen atoms in a quantum-
90
HOW WE KNOW: Peptide Bonds Are (Mostly) Flat
Edison, A.S. 2001. Linus Pauling and the planar peptide bond. Nat. Struct. Mol. Biol. 8:201–
MacArthur, M.W., and J.M. Thornton. 1996. Deviations from planarity of the peptide bond in peptides and proteins. J. Mol. Biol. 264:1180–
Pauling, L., R.B. Corey, and H.R. Branson. 1951. The structure of proteins: Two hydrogen-

More than 50 years ago, Linus Pauling realized that the planar nature (flatness) of peptide bonds was an important constraint on polypeptides, leading him to the prediction of key elements of protein structure: the α helix and the β-pleated sheet (described in Chapter 4). But are peptide bonds truly flat? Two dominant resonance structures of the N–
Today, the availability of thousands of protein and peptide structures makes it possible to conduct statistical surveys of peptide bonds in natural proteins. Janet Thornton and her colleagues showed that many such structures contain deviations from planar peptide bonds. Using a subset of available high-
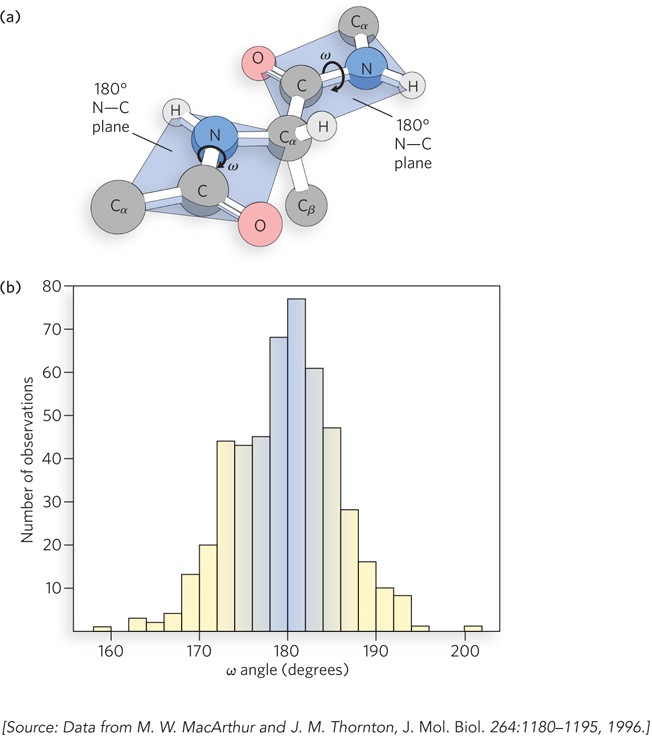
91