Section 11.2 Exercises

CLARIFYING THE CONCEPTS

Question 11.36

1. Explain what a contingency table is. (p. 646)

11.2.1

Tabular summary of the relationship between two categorical variables. 3. The two-sample test for the difference in proportions from Chapter 10 is for comparing proportions of two independent populations, and the test for homogeneity of proportions is for comparing proportions of independent populations.

Question 11.37

2. Explain in your own words what is meant by a test for independence. (p. 646)

Question 11.38

3. What is the difference between the test for homogeneity of proportions and the two-sample test for the difference in proportions from Chapter 10? (p. 651)

Question 11.39

4. Explain how the expected frequencies are calculated without using the shortcut method. (p. 647)

PRACTICING THE TECHNIQUES

image CHECK IT OUT!

To do Check out Topic
Exercises 5–10 Example 6 Calculating expected
frequencies
Exercises 11–14 Example 7 test for
independence: critical-value method
Exercises 15–18 Example 8 test for
independence: p-value
method
Exercises 19–26 Example 9 test for homogeneity
of proportions

For Exercises 5–10, the observed frequencies are provided in a contingency table of two categorical variables. Find the expected frequencies, on the assumption that the variables are independent.

Question 11.40

5.

A1 A2
B1 10 20
B2 12 18

11.2.5

A1 A2 Total
B1 11 19 30
B2 11 19 30
Total 22 38 60

Question 11.41

6.

C1 C2
D1 50 100
D2 60 90

Question 11.42

7.

E1 E2 E3
F1 30 20 10
F2 35 24 8

11.2.7

E1 E2 E3 Total
F1 30.71 20.79 8.50 60
F2 34.29 23.21 9.50 67
Total 65 44 18 127

Question 11.43

8.

G1 G2
H1 10 8
H2 8 10
H3 9 9

Question 11.44

9.

I1 I2 I3
J1 100 90 105
J2 50 60 55
J3 25 15 20

11.2.9

I1 I2 I3 Total
J1 99.2788 93.6058 102.1154 295
J2 55.5288 52.3558 57.1154 165
J3 20.1923 19.0385 20.7692 60
Total 174.9999 165.0001 180 520

Question 11.45

10.

K1 K2 K3 K4
L1 40 70 90 100
L2 20 40 60 70
L3 30 65 65 70

658

For Exercises 11–14, test whether or not the variables are independent.

  1. State the hypotheses.
  2. Verify that the conditions for performing the test for independence are met.
  3. Find and state the rejection rule.
  4. Calculate .
  5. Compare with . State the conclusion and the interpretation.

Question 11.46

11. Exercise 5, level of significance

11.2.11

(a) : Variable and Variable are independent. : Variable and Variable are dependent.

(b)

A1 A2 Total
B1 11 19 30
B2 11 19 30
Total 22 38 60

Since none of the expected frequencies is less than 1 and none of the expected frequencies is less than 5, the conditions for performing the test for independence are met. (c) 3.841. Reject if . (d) 0.2871 (e) Since is not , we do not reject . There is insufficient evidence that variable and variable are dependent.

Question 11.47

12. Exercise 7, level of significance

Question 11.48

13. Exercise 9, level of significance

11.2.13

(a) : Variable and Variable are independent. : Variable and Variable are dependent.

(b)

I1 I2 I3 Total
J1 99.2788 93.6058 102.1154 295
J2 55.5288 52.3558 57.1154 165
J3 20.1923 19.0385 20.7692 60
Total 174.9999 165.0001 180 520

Since none of the expected frequencies is less than 1 and none of the expected frequencies is less than 5, the conditions for performing the test for independence are met. (c) 13.277. Reject if . (d) 4.000 (e) Since is not , we do not reject . There is insufficient evidence that variable and variable are dependent.

Question 11.49

14. Exercise 9, level of significance

For Exercises 15–18, test whether or not the variables are independent.

  1. State the hypotheses and the rejection rule for the p-value method, and verify that the conditions for performing the test for independence are met.
  2. Find .
  3. Calculate the p-value.
  4. Compare the p-value with . State the conclusion

Question 11.50

15. Exercise 6, level of significance

11.2.15

(a) : Variable and Variable are independent. : Variable and Variable are dependent. Reject if the -value .

C1 C2 Total
D1 55 95 150
D2 55 95 150
Total 110 190 300

Since none of the expected frequencies is less than 1 and none of the expected frequencies is less than 5, the conditions for performing the test for independence are met. (b) 1.4354 (c) - (d) Since the -value is not , we do not reject . There is insufficient evidence that variable and variable are dependent.

Question 11.51

16. Exercise 8, level of significance

Question 11.52

17. Exercise 10, level of significance

11.2.17

(a) : Variable and Variable are independent. : Variable and Variable are dependent. Reject if -value .

K1 K2 K3 K4 Total
L1 37.5 72.92 89.58 100 300
L2 23.75 46.18 56.74 63.33 190
L3 28.75 55.90 68.68 76.67 230
Total 90 175 215 240 720

Since none of the expected frequencies is less than 1 and none of the expected frequencies is less than 5, the conditions for performing the test for independence are met. (b) (c) -value (d) Since the -value is not , we do not reject . There is insufficient evidence that variable and variable are dependent.

Question 11.53

18. Exercise 10, level of significance

For Exercises 19–22, test whether or not the proportions of successes are the same for all populations.

  1. State the hypotheses.
  2. Calculate the expected frequencies and verify that the conditions for performing the test for homogeneity of proportions are met.
  3. Find and state the rejection rule. Use level of significance .
  4. Find .
  5. Compare with . State the conclusion and the interpretation.

Question 11.54

19.

Sample 1 Sample 2 Sample 3
Successes 10 20 30
Failures 20 45 62

11.2.19

(a) . : Not all the proportions in are equal.

(b)

Sample 1 Sample 2 Sample 3 Total
Successes 9.63 20.86 29.52 60.01
Failures 20.37 44.14 62.48 126.99
Total 30 65 92 187

Since none of the expected frequencies is less than 1 and none of the expected frequencies is less than 5, the conditions for performing the test for homogeneity of proportions are met. (c) 5.991. Reject if . (d) 0.0847 (e) Since is not , we do not reject . There is insufficient evidence that not all the proportions in are equal.

Question 11.55

20.

Sample 1 Sample 2 Sample 3
Successes 50 50 100
Failures 200 210 425

Question 11.56

21.

Sample 1 Sample 2 Sample 3 Sample 4
Successes 10 15 20 25
Failures 15 24 32 40

11.2.21

(a) . : Not all the proportions in are equal.

(b)

Sample 1 Sample 2 Sample 3 Sample 4 Total
Successes 9.67 15.08 20.11 25.14 70
Failures 15.33 23.92 31.89 39.86 111
Total 25 39 52 65 181

Since none of the expected frequencies is less than 1 and none of the expected frequencies is less than 5, the conditions for performing the test for homogeneity of proportions are met. (c) 7.815. Reject if . (d) 0.0215 (e) Since is not , we do not reject . There is insufficient evidence that not all the proportions in are equal.

Question 11.57

22.

Sample 1 Sample 2 Sample 3 Sample 4
Successes 100 150 200 250
Failures 150 240 320 400

For Exercises 23–26, test whether or not the proportions of successes are the same for all populations.

  1. State the rejection rule for the p-value method using level of significance , calculate the expected frequencies, and verify that the conditions for performing the test for homogeneity of proportions are met.
  2. Find .
  3. Calculate the p-value.
  4. Compare the p-value with . State the conclusion and the interpretation.

Question 11.58

23.

Sample 1 Sample 2 Sample 3
Successes 30 60 90
Failures 10 25 50

11.2.23

(a) . : Not all the proportions in are equal. Reject if the -value .

Sample 1 Sample 2 Sample 3 Total
Successes 27.17 57.74 95.09 180
Failures 12.83 27.26 44.91 85
Total 40 85 140 265

Since none of the expected frequencies is less than 1 and none of the expected frequencies is less than 5, the conditions for performing the test for homogeneity of proportions are met. (b) 2.0468 (c) -value . (d) Since the -value is not , we do not reject . There is insufficient evidence that not all the proportions in are equal.

Question 11.59

24.

Sample 1 Sample 2 Sample 3
Successes 100 120 140
Failures 20 25 30

Question 11.60

25.

Sample 1 Sample 2 Sample 3 Sample 4
Successes 10 12 24 32
Failures 6 10 15 30

11.2.25

(a) . : Not all the proportions in are equal. Reject if the -value .

Sample 1 Sample 2 Sample 3 Sample 4 Total
Successes 8.98 12.35 21.88 34.79 78
Failures 7.02 9.65 17.12 27.21 61
Total 16 22 39 62 139

Since none of the expected frequencies is less than 1 and none of the expected frequencies is less than 5, the conditions for performing the test for homogeneity of proportions are met. (b) 1.263 (c) -value .

(d) Since the -value is not , we do not reject . There is insufficient evidence that not all the proportions in are equal.

Question 11.61

26.

Sample 1 Sample 2 Sample 3 Sample 4
Successes 100 200 300 400
Failures 30 70 150 300

APPLYING THE CONCEPTS

Question 11.62

worktask

27. Email, Phone, or in Person? What is the most effective way to handle a task at work: by email, by phone, or in person? Well, you probably say, it depends on the task. The Pew Internet and American Life Project Email at Work Survey surveyed 1000 randomly selected work email users, who chose the following methods as the best for handling certain work tasks. Test whether the proportions who favor email differ between the two tasks, using level of significance and the p-value method.

Task By email By phone or
in person
Edit or review documents 670 330
Arrange meetings or
appointments		 630 370

11.2.27

. : Not all the proportions in are equal. Reject if -value . Since none of the expected frequencies is less than 1 and none of the expected frequencies is less than 5, the conditions for performing the test for homogeneity of proportions are met. . -value . Since the -value is not , we do not reject . There is insufficient evidence that the proportions who favor email differ between the two tasks.

Question 11.63

computerweight

28. Computer Usage and Weight in Children. The National Center for Health Statistics conducted a survey of children 12–15 years old. Three random samples were taken, one sample of normal or underweight children, one sample of overweight children, and one sample of obese children. The surveys noted whether the children used a computer for more than two hours per day. The results are presented in the following table. Test whether the population proportions of children who use the computer for more than two hours per day are the same for the three weight statuses, using level of significance .

659

Normal or
underweight		 Overweight Obese Total
Using computer
more than two
hours per day		 114 28 52 194
Using computer
two hours or
less per day		 355 96 121 572
Total 469 124 173 766

Question 11.64

weatherdeaths

29. Weather-Related Deaths. The Centers for Disease Control track the numbers of deaths due to weather-related causes. Is there is a difference in the pattern of deaths for young people and older people? The following table shows the number of deaths for three weather-related categories, for young people ages 15–24 and older people ages 75–84. Test, using level of significance , whether cause of death and age group are independent.

Age
group		 Heat-
related		 Cold-
related		 Floods/
storms/
lightning		 Total
15–24 106 286 97 489
75–84 490 1010 53 1553
Total 596 1296 150 2042
Table 11.56: Weather-related cause of death

11.2.29

: Cause of death and age group are independent. : Cause of death and age group are dependent.

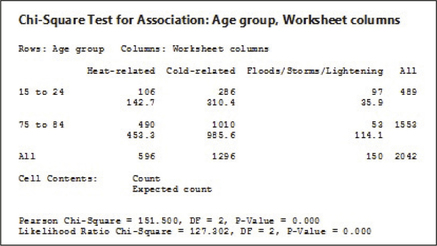
image

From the Minitab output above, none of these expected frequencies is less than one, and none of the expected frequencies is less than five. Therefore, the conditions for performing the test for independence are met. Reject if the . . . The is less than or equal to . Therefore, we reject . Evidence exists, at level of significance , that the variables Cause of death and age group are dependent.

Question 11.65

30. Using Graphical Evidence. Sick of spam (unsolicited broadcast email)? Do you get more spam at your work, school, or home email address? The Pew Internet and American Life Project Email at Work Survey examined the proportion of spam in email users' work and home email accounts. Two random samples were used, one of work email and one of personal email. Using only the information in the clustered bar graph below, would you conclude that the proportion of those who report “a lot of spam” is the same for work email and personal email? Why?

image

Question 11.66

31. Spam, Spam, Spam. Continue your work from the previous exercise. The following contingency table shows the actual percentages in the graph above based on samples of size 100 for each of work email and personal email. Test whether the proportions who report “a lot of spam” are the same for work email and personal email, using level of significance . Does your conclusion agree with your conjecture in the previous exercise?

None Some A lot
Work email 53% 36% 11%
Personal email 22% 48% 30%

11.2.31

. : Not all the proportions in are equal. Reject if -value . Since none of the expected frequencies is less than 1 and none of the expected frequencies is less than 5, the conditions for performing the test for homogeneity of proportions are met. . -value ≈ 0. Since -value , we reject . There is evidence that the population proportions who report “a lot of spam” are not the same for work email and personal email. Yes.

Question 11.67

games

32. Gender Differences in Computer/Video/Online Gaming. The Pew Internet and American Life Project collected data on the College Students Gaming Survey. Among the questions they asked 1720 randomly selected college students was “Which one of the following do you play the most: video games, computer games, or online games?” The results are summarized by gender in the following contingency table.

Video
games		 Computer
games		 Internet
games
Male 616 221 139
Female 198 372 174
  1. Before you perform the hypothesis test, what result might you expect? Look over the data set carefully to see whether you can detect significant differences between the levels of the variables. Then see whether your hypothesis test bears out your intuition.
  2. Test whether gender and game type are independent, using level of significance .

Question 11.68

33. Online Dating. A Pew Internet and American Life Project study reported that the proportion of urban residents who use online dating is 13%, whereas the proportion for suburban residents is 10% and the proportion for rural residents is 9%.7 Test, using level of significance , whether differences exist among the population proportions of residents from the three categories who use online dating. Assume that each sample size was 1000. (Hint: The null hypothesis assumes that all proportions are equal.)

11.2.33

. : Not all the proportions in are equal. Reject if -value . Since none of the expected frequencies is less than 1 and none of the expected frequencies is less than 5, the conditions for performing the test for homogeneity of proportions are met. . -value . Since -value , we reject . There is evidence that the population proportions of residents from the three categories who use online dating are not all the same.

WORKING WITH LARGE DATA SETS

Use Minitab or Excel for each of Exercises 34–38.

Goals of Middle School Students. Open the Goals data set. The subjects are students in grades 4, 5, and 6, from three school districts in Michigan. The students were asked which of the following was most important to them: good grades, athletic ability, or popularity. Information about the students' age, gender, race, and grade was also gathered, as well as whether their school was in an urban, suburban, or rural setting.8

Question 11.69

goals

34. How many observations are in the data set? How many variables?

Question 11.70

goals

35. Comparing gender and goals.

  1. Looking at the data, do you think that boys and girls at this age differ in what is most important to them: grades, popularity, or sports? In other words, do you think that the variables gender and goals are dependent or independent?

    660

  2. Perform the test for independence, using level of significance .

11.2.35

(a) Dependent (b) Since the -value ≈ 0, -value . Thus we reject . There is evidence that gender and goals are dependent.

Question 11.71

goals

36. Comparing gender and grade.

  1. Looking at the data, do you think that the ratio of females to males differs significantly from grade to grade? In other words, do you think that the variables gender and grade are dependent or independent?
  2. Perform the test for independence, using level of significance .

Question 11.72

goals

37. Comparing goals and school setting.

  1. Looking at the data, do you think that the setting of the school (urban, suburban, or rural) affects the goals of the students? Or do you think that it has no effect? In other words, do you think that the variables urb_rur and goals are independent or dependent?
  2. Perform the test for independence, using level of significance .

11.2.37

(a) Dependent (b) Since the -value , -value . Thus we reject . There is evidence that urb_rural and goals are dependent.

Question 11.73

goals

38. Comparing grades and goals.

  1. One thing we know for sure is that, as students get older, they get more serious and grades get more important to them (don't they?). So we would expect that the variables grade and goals would be dependent, wouldn't we? Is this borne out by looking at the data?
  2. Perform the test for independence, using level of significance .

Question 11.74

1970draft

39. 1970 Military Draft. Is there evidence that the 1970 military draft, conducted at the height of the Vietnam War, was not truly random? For this exercise, birth dates were ranked from 1 (for the first date drawn) to 366 (the last date drawn). In 1970, only those young men with birth date rankings up to 195 were eventually drafted. Because 195 of the 366 dates were “drafted,” the overall proportion of “drafted dates” is . Assuming the draft was truly random, we do not expect the proportion of “drafted dates” to vary significantly from month to month. In other words, the proportion of “drafted dates” should be about the same for each of the 12 months. We therefore define a multinomial random variable drafted, with the months as categories. The monthly counts of dates not drafted and drafted are provided here. (For example, for April, 12 dates out of 30 were chosen to be drafted.) Test whether the proportions of “drafted dates” are equal for all months, using level of significance .

Month Dates not drafted Dates drafted All
Jan. 17 14 31
Feb. 16 13 29
Mar. 21 10 31
Apr. 18 12 30
May 17 14 31
June 16 14 30
July 13 18 31
Aug. 12 19 31
Sept. 11 19 30
Oct. 17 14 31
Nov. 8 22 30
Dec. 5 26 31
All 171 195 366

11.2.39

. : Not all the proportions in are equal. Reject if -value . . -value . Since -value , we reject . There is evidence that the population proportion of “drafted dates” is not equal for all months.

Question 11.75

1971draft

40. 1971 Military Draft. Criticism of the 1970 draft lottery led the U.S. Selective Service Bureau to focus on making sure that the 1971 draft lottery was truly random. Were their efforts successful? The results of the 1971 draft lottery are shown here (365 days). The Selective Service reports that all birth dates with a rank of 125 or less were chosen for the draft. Perform a test for homogeneity of proportions to determine whether the population proportions of “drafted dates” per month were all equal, using level of significance .

Month Dates not drafted Dates drafted
Jan. 19 12
Feb. 19 9
Mar. 21 10
Apr. 21 9
May 22 9
June 21 9
July 19 12
Aug. 18 13
Sept. 23 7
Oct. 19 12
Nov. 16 14
Dec. 22 9