2 Describing Data Using Graphs and Tables

Section 2.3 Exercises

CLARIFYING THE CONCEPTS

Question 2.279

1. Explain the difference between a frequency distribution and a cumulative frequency distribution. (p. 87)

2.3.1

A frequency distribution gives the frequency counts for each class (grouped or ungrouped). A cumulative frequency distribution gives the number of values that are less than or equal to the upper limit of a given class for grouped data or it gives the number of values that are less than or equal to a given number for ungrouped data.

Question 2.280

2. Explain the difference between a cumulative frequency distribution and a cumulative relative frequency distribution. (p. 87)

Question 2.281

3. What is the graphical equivalent of a cumulative frequency distribution? (p. 88)

2.3.3

Ogive.

Question 2.282

4. Explain how to construct an ogive. (p. 88)

Question 2.283

5. What do we call data that are analyzed with respect to time? (p. 89)

2.3.5

Time series data.

Question 2.284

6. Explain how to construct a time series plot. (p. 89)

PRACTICING THE TECHNIQUES

CHECK IT OUT!

To do	Check out	Topic
Exercises 9–12	Example 22	Cumulative frequency and cumulative relative frequency distributions
Exercises 13–16	Example 23	Ogives
Exercises 17–18	Examples 24 and 25	Time series plots

The U.S. Census Bureau reported in 2014 that the relative frequency of the age of the head of the household is as shown in Table 38 (for those with heads of households younger than age 65). Use Table 38 to construct the following graphical summaries of the variable age.

Table 2.87: TABLE 38 Relative frequency distribution of age

Age	Frequency (millions)	Relative frequency
	22.7	0.24
	22.2	0.24
	25.8	0.27
	23.2	0.25

Question 2.285

7. Cumulative frequency distribution

2.3.7

Frequency (millions)	Relative frequency	Cumulative frequency (millions)	Cumulative relative frequency
22.7	0.24	22.7	0.24
22.2	0.24
25.8	0.27
23.2	0.25

Question 2.286

8. Cumulative relative frequency distribution

For Exercises 9–12, do the following:

Construct a cumulative frequency distribution for the indicated data.
Build a cumulative relative frequency distribution for the indicated data.

Question 2.287

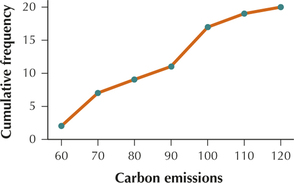
9. Carbon emissions data from Table 20 on page 63.

2.3.9

(a) and (b)

Carbon emissions	Frequency	Relative frequency	Cumulative frequency	Cumulative relative frequency
	2		2	0.10
	5
	2
	2
	6
	2
	1
Total	20	20/20 = 1.00

Question 2.288

10. Unemployment data from Table 22 on page 65.

Question 2.289

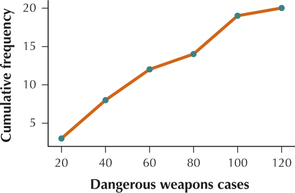
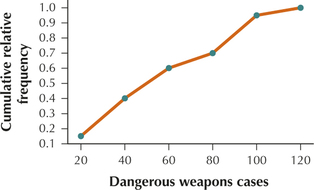
11. Dangerous weapons data from Table 23 on page 68.

2.3.11

(a) and (b)

Dangerous weapons cases	Frequency	Relative frequency	Cumulative frequency	Cumulative relative frequency
	3		3	0.15
	5		8	0.40
	4		12	0.60
	2		14	0.70
	5		19	0.95
	1		20	1.00
Total	20	1.00

Question 2.290

12. Brooklyn frauds 2013 data from Table 31 on page 82.

For Exercises 13–16, do the following:

Construct a frequency ogive for the indicated data.
Build a relative frequency ogive for the indicated data.

Question 2.291

13. Carbon emissions data from Table 20 on page 63.

2.3.13

(a)

(b)

Question 2.292

14. Unemployment data from Table 22 on page 65.

Question 2.293

15. Dangerous weapons data from Table 23 on page 68.

2.3.15

(a)

(b)

Question 2.294

16. Brooklyn frauds 2013 data from Table 31 on page 82.

Question 2.295

harassment

17. The following time series data represent the number of aggravated harassment cases handled by New York City Police Precinct 1 from 2000 to 2013.

Construct the time series graph of the data.
Describe any patterns you see.

Year	2000	2001	2002	2003	2004	2005	2006
Cases	547	568	476	475	450	445	379
Year	2007	2008	2009	2010	2011	2012	2013
Cases	424	404	425	429	343	400	400

2.3.17

(a)

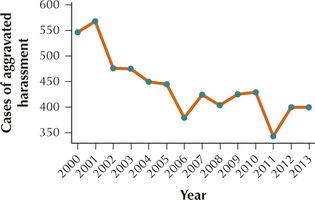
(b) Generally decreasing

Question 2.296

petitlarceny5

18. The following time series data represent the number of petit larceny cases handled by New York City Police Precinct 5 from 2000 to 2013.

Construct the time series graph of the data.
Describe any patterns you see.

Year	2000	2001	2002	2003	2004	2005	2006
Cases	909	846	834	793	798	871	808
Year	2007	2008	2009	2010	2011	2012	2013
Cases	859	1020	1014	1263	1197	1240	1288

APPLYING THE CONCEPTS

Question 2.297

19. Unemployment Rate. The frequency ogive below represents the unemployment rate (in percentages) for 367 cities nationwide.⁹

What is the class width?
What is the upper class limit of the leftmost class?
What is the class midpoint of the leftmost class?

2.3.19

(a) 0.8 (b) 2.39 (c) 1.99

Question 2.298

20. Refer to the frequency ogive of unemployment rates.

About how many cities have unemployment rates 3.99 and below?
About how many cities have unemployment rates 5.59 and below?
About how many cities have unemployment rates 5.6 and above?

Question 2.299

maunaloa2

21. Atmospheric Carbon Dioxide. Table 39 contains the amount of carbon dioxide in parts per million (ppm) found in the atmosphere above Mauna Loa, Hawaii, measured monthly from October 2012 to September 2013.

Construct a time series plot of these data.
Describe the pattern you see.

Table 2.93: TABLE 39 Atmospheric carbon dioxide at Mauna Loa, October 2012 to September 2013

Month	Carbon dioxide (ppm)	Month	Carbon dioxide (ppm)
Oct.	391.01	Apr.	398.35
Nov.	392.81	May	399.76
Dec.	394.28	June	398.58
Jan.	395.54	July	397.20
Feb.	396.80	Aug.	395.15
Mar.	397.31	Sept.	393.51

Table 2.93: Source: Dr. Pieter Tans, Earth System Research Laboratory, National Oceanic and Atmospheric Administration, www.esrl.noaa.gov/gmd/ccgg/trends.

2.3.21

(a)

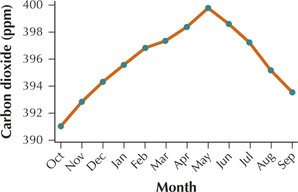
(b) The level of carbon dioxide increases from October to May and decreases from May to September.

Question 2.300

22. Medicare. Table 40 contains a time series of the number of enrollees (in millions) in Medicare from 1987 to 2012.

Table 2.94: TABLE 40 Medicare enrollees (in millions)

Year	Enrollees	Year	Enrollees	Year	Enrollees
1987	30	1996	35	2005	40
1988	31	1997	36	2006	40
1989	31	1998	36	2007	41
1990	32	1999	37	2008	43
1991	33	2000	38	2009	43
1992	33	2001	38	2010	45
1993	33	2002	39	2011	47
1994	34	2003	40	2012	49
1995	35	2004	40

Table 2.94: Source: U.S. Census Bureau.

Question 2.301

23. Refer to your time series plot from the preceding exercise. The increase in the number of enrollees is fairly constant and then becomes steeper. In what year does this change occur?

2.3.23

2009

Agricultural Exports. For Exercises 24–26, refer to Table 41. The table gives the value of agricultural exports (in billions of dollars) from the top 20 U.S. states in 2009.

Table 2.95: TABLE 41 Agricultural exports (in billions of dollars)

State	Exports	State	Exports
California	12.5	Arkansas	2.6
Iowa	6.5	North Dakota	5.2
Texas	4.7	Ohio	2.7
Illinois	5.5	Florida	2.1
Nebraska	4.8	Wisconsin	2.2
Kansas	4.7	Missouri	2.7
Minnesota	4.3	Georgia	1.8
Washington	3.0	Pennsylvania	1.7
North Carolina	2.9	Michigan	1.6
Indiana	3.1	South Dakota	2.3

Table 2.95: Source: U.S. Department of Agriculture.

Question 2.302

agriexports

24. Construct a cumulative frequency distribution of agricultural exports. Start at $0 and use class widths of $2 billion.

How many states have exports of less than $4 billion?
How many states have exports of less than $6 billion?
How many states have exports of at least $6 billion?

Question 2.303

agriexports

25. Construct a cumulative relative frequency distribution of agricultural exports. Start at $0 and use class widths of $2 billion.

What proportion of states has exports of less than $4 billion?
What proportion of states has exports of less than $6 billion?
What proportion of states has exports of at least $6 billion?

2.3.25

Agricultural exports (in billions of dollars)	Frequency	Relative frequency	Cumulative relative frequency
	3	0.15	0.15
	9	0.45	0.60
	6	0.30	0.90
	1	0.05	0.95
	0	0	0.95
	0	0	0.95
	1	0.05	1.00
Total	20	1.00

(a) 0.60 (b) 0.90 (c) 0.10

Question 2.304

agriexports

26. Use your cumulative relative frequency distribution to construct a relative frequency ogive of agricultural exports.

Question 2.305

percapitaincome

27. Per Capita Income. The following data represent the per capita income in the United States from 1967 to 2012, in thousands of constant (2012) dollars.

Year	Per capita income $1000s	Year	Per capita income $1000s	Year	Per capita income $1000s
1967	15	1983	21	1998	28
1968	16	1984	22	1999	29
1969	17	1985	22	2000	30
1970	17	1986	23	2001	30
1971	17	1987	24	2002	29
1972	18	1988	24	2003	29
1973	19	1989	25	2004	29
1974	19	1990	25	2005	29
1975	19	1991	24	2006	30
1976	19	1992	24	2007	30
1977	20	1993	25	2008	29
1978	21	1994	25	2009	28
1979	21	1995	26	2010	28
1980	21	1996	26	2011	28
1981	21	1997	27	2012	28
1982	21

Table 2.97: Source: U.S. Census Bureau.

Construct a time series plot of the per capita income.
A fairly constant increasing trend occurs. In what year does this trend appear to end?

2.3.27

(a)

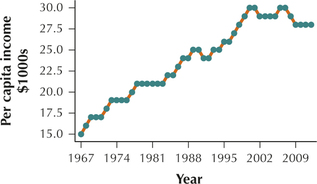
(b) 2008

Question 2.306

flrainfall

28. Rainfall in Fort Lauderdale. The following data represent the total monthly rainfall (in inches) in 2013 in Fort Lauderdale, Florida, as reported by the U.S. Historical Climatology Network.

Jan.	0.55	July	15.54
Feb.	2.39	Aug.	3.33
Mar.	0.15	Sept.	6.78
Apr.	3.99	Oct.	5.8
May	13.63	Nov.	11.61
June	13.63	Dec.	1.11

Construct a time series plot of the data.
Is it wetter in summer or winter in Fort Lauderdale?

Question 2.307

29. In Exercise 28, what if we add 3 inches to each month's rainfall amount. Describe how this would affect the time series plot. What would change? What would stay the same?

2.3.29

The only change would be that the entire time series graph would shift up 3 units. The horizontal scale would stay the same and the shape of the graph would stay the same.

Question 2.308

12thsmokers

30. Cigarette use among 12th-Graders. Table 42 presents the percentages of 12th-graders who smoke cigarettes, for the years 1980–2009.

Construct a time series plot of the data.
Describe any trends that you see.

Table 2.99: TABLE 42 12th-graders who smoke

Year	Percent	Year	Percent
1980	30.5	1995	33.5
1981	29.4	1996	34.0
1982	30.0	1997	36.5
1983	30.3	1998	35.1
1984	29.3	1999	34.6
1985	30.1	2000	31.4
1986	29.6	2001	29.5
1987	29.4	2002	26.7
1988	28.7	2003	24.4
1989	28.6	2004	25.0
1990	29.4	2005	23.2
1991	28.3	2006	21.6
1992	27.8	2007	21.6
1993	29.9	2008	20.4
1994	31.2	2009	20.1

Table 2.99: Source: Monitoring the Future study, University of Michigan.

Question 2.309

miamideptcorrections

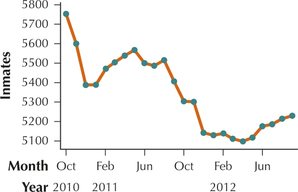
31. Miami arrests. The Miami-Dade Department of Corrections and Rehabilitation publishes its monthly average daily population of inmates in its Annual Report. Table 43 shows the average daily number of inmates from October 2010 through September 2012. Construct a time series graph of the data.

Table 2.100: TABLE 43 Average monthly inmate population, Miami-Dade Department of Corrections

Month	Inmates	Month	Inmates	Month	Inmates
Oct 2010	5753	Jun 2011	5500	Feb 2012	5138
Nov 2010	5600	Jul 2011	5486	Mar 2012	5111
Dec 2010	5387	Aug 2011	5515	Apr 2012	5097
Jan 2011	5388	Sep 2011	5406	May 2012	5117
Feb 2011	5471	Oct 2011	5304	Jun 2012	5175
Mar 2011	5504	Nov 2011	5201	Jul 2012	5185
Apr 2011	5538	Dec 2011	5141	Aug 2012	5214
May 2011	5567	Jan 2012	5129	Sept 2012	5229

Table 2.100: Source: www.miamidade.gov/corrections/library/Annual-Report-2011-2012.pdf.

2.3.31

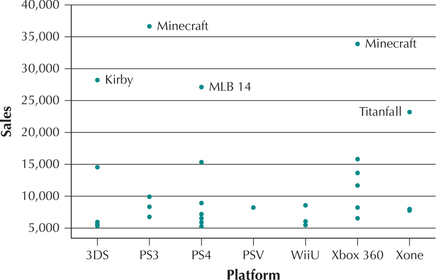
Individual Value Plot. Have you played Minecraft? On which platform did you play it? Figure 53 represents an individual value plot of video game sales for the week of May 17, 2014, separated by platform. An individual value plot is similar to a dotplot for different categories, which is rendered vertically. Each dot represents the sales for a particular video game. The top five sellers are labeled. Minecraft was the biggest seller that week, with the PS3 version slightly outselling the Xbox 360 version. Use this information for Exercises 32 and 33.

Question 2.310

32. Which platform is indicated by MLB 14?

Question 2.311

33. Are sales higher for the top-performing title for Xbox One (“Xone”) or 3DS?

2.3.33

3DS

Figure 2.53: FIGURE 53 Individual value plot of video games sales, by platform.

WORKING WITH LARGE DATA SETS

Assault.

Open the Assault data set, which contains the number of third-degree assaults per precinct for the years 2000–2013. Use technology to do the following:

Question 2.312

34. Construct a time series plot of the number of third-degree assaults in Precinct 1 from 2000 to 2013. Describe any patterns you see.

Question 2.313

35. For each year, calculate the sum of the number of third-degree assaults, across all precincts.

2.3.35

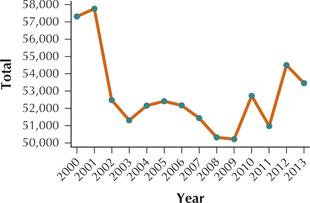
Question 2.314

36. Build a time series plot of the total number of third-degree assaults, across all precincts. Describe any patterns you see.