Section 2.1 Exercises

CLARIFYING THE CONCEPTS

Question 2.1

1. Why do we use graphical and tabular methods to summarize data? What's wrong with simply reporting the raw data? (p. 40)

2.1.1

We use graphical and tabular form to summarize data in order to organize it in a format where we can better assess the information. If we just report the raw data, it may be extremely difficult to extract the information contained in the data.

Question 2.2

2. What's the difference between a frequency distribution and a relative frequency distribution? (p. 42)

Question 2.3

3. True or false: For a given data set, a frequency bar graph and a relative frequency bar graph look alike, except for the scale on the vertical axis. (p. 43)

2.1.3

True.

Question 2.4

4. True or false: A pie chart is used to represent quantitative data. (p. 44)

Question 2.5

5. What should be the sum of the frequencies in a frequency distribution? (p. 41)

2.1.5

The sample size, .

Question 2.6

6. What should be the sum of the relative frequencies in a relative frequency distribution? (p. 42)

Question 2.7

7. In a crosstabulation, the “Total” column represents what? How about the “Total” row? (p. 46)

2.1.7

The row totals; the column totals

Question 2.8

8. What does the number in the lower right corner of the crosstabulation represent? What should this number be equal to? (p. 48)

Question 2.9

9. True or false: Each set of bars in a clustered bar graph represents a single category of one variable across all the categories of the other categorical variable. (p. 48)

2.1.9

True

Question 2.10

10. True or false: A clustered bar graph cannot be constructed for relative frequency data. (p. 48)

PRACTICING THE TECHNIQUES

image CHECK IT OUT!

To do Check out Topic
Exercises 11–14
and 23–28		 Examples 1
and 2 		Frequency distributions
and relative frequency
distributions.
Exercises 15–18
and 29–34		 Example 3 Bar graphs
Exercises 19–20
and 35–36		 Example 4 Pie charts
Exercises 21, 37,
41, and 45		 Example 5 Constructing
crosstabulations
Exercises 22,
38–40, 42–44,
and 46–56		 Example 6 Working with tabular
data
Exercises 57–60 Example 7 Clustered bar graphs

Table 12 contains data regarding how all the counties in Nevada voted in the 2012 presidential election (Dem = Democrat, Rep = Republican), as well as the size of the county in terms of number of voters (Small = at most 10,000; Medium = 10,001 to 100,000; Large = over 100,000). Use Table 12 to construct the indicated distribution or graph for Exercises 11–22.

Table 2.13: TABLE 12 2012 Presidential election results for all nevada counties
County Vote Size County Vote Size
Carson City Rep Medium Lincoln Rep Small
Churchill Rep Medium Lyon Rep Medium
Clark Dem Large Mineral Rep Small
Douglas Rep Medium Nye Rep Medium
Elko Rep Medium Pershing Rep Small
Esmerelda Rep Small Storey Rep Small
Eureka Rep Small Washoe Dem Large
Humboldt Rep Small White Pine Rep Small
Lander Rep Small

54

Question 2.11

nevadacounties

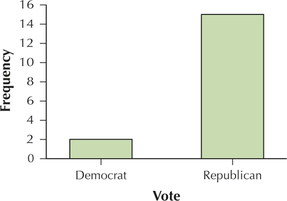
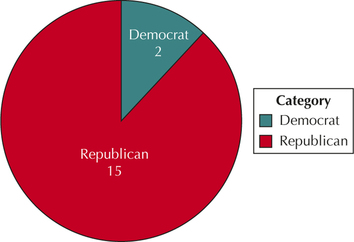
11. Frequency distribution of the variable vote.

2.1.11

Vote Frequency
Republican 15
Democrat 2

Question 2.12

nevadacounties

12. Relative frequency distribution of the variable vote.

Question 2.13

nevadacounties

13. Frequency distribution of the variable size.

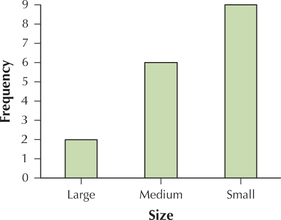
2.1.13

Size Frequency
Small 9
Medium 6
Large 2

Question 2.14

nevadacounties

14. Relative frequency distribution of the variable size.

Question 2.15

nevadacounties

15. Frequency bar graph of vote.

2.1.15

image

Question 2.16

nevadacounties

16. Relative frequency bar graph of vote.

Question 2.17

nevadacounties

17. Frequency bar graph of size.

2.1.17

image

Question 2.18

nevadacounties

18. Relative frequency bar graph of size.

Question 2.19

nevadacounties

19. Pie chart for vote.

2.1.19

image

Question 2.20

nevadacounties

20. Pie chart for size.

Question 2.21

nevadacounties

21. Crosstabulation of the variables vote and size.

2.1.21

Large Medium Small Total
Democrat 2 0 0 2
Republican 0 6 9 15
Total 2 6 9 17

Question 2.22

nevadacounties

22. Nevada's electoral votes actually went to the Democratic candidate in 2012. Use the crosstabulation from the previous exercise to explain how this might have happened, even though the Republican candidate carried all but two of the counties.

The sinking of the Titanic was one of the greatest disasters in maritime history. The data set Titanic contains information on 2202 passengers and crew, including their class (1st class, 2nd class, 3rd class, or crew), their gender, and whether they survived. Table 13 contains a random sample of size 20 from this data set. Use Table 13 for Exercises 23–48. For Exercises 23–37, construct the indicated distribution or graph.

Table 2.17: TABLE 13 Class, gender, and survival status of 20 passengers and crew of the Titanic
Class Gender Survived Class Gender Survived
3rd Female No 1st Female Yes
Crew Male No 1st Male Yes
3rd Female Yes Crew Male No
Crew Male No 3rd Male Yes
Crew Male Yes Crew Male No
3rd Male Yes 2nd Male Yes
Crew Male No 3rd Male No
Crew Male No Crew Male No
2nd Male No 2nd Female Yes
Crew Male Yes 2nd Male No

Question 2.23

titanicsample

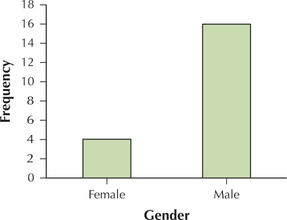
23. Frequency distribution of the variable gender.

2.1.23

Gender Frequency
Male 16
Female 4

Question 2.24

titanicsample

24. Relative frequency distribution of the variable gender.

Question 2.25

titanicsample

25. Frequency distribution of the variable survived.

2.1.25

Survived Frequency
Yes 9
No 11

Question 2.26

titanicsample

26. Relative frequency distribution of the variable survived.

Question 2.27

titanicsample

27. Frequency distribution of the variable class.

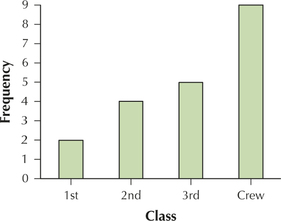
2.1.27

Class Frequency
1st class 2
2nd class 4
3rd class 5
Crew 9

Question 2.28

titanicsample

28. Relative frequency distribution of the variable class.

Question 2.29

titanicsample

29. Frequency bar graph of gender.

2.1.29

image

Question 2.30

titanicsample

30. Relative frequency bar graph of gender.

Question 2.31

titanicsample

31. Frequency bar graph of survived.

2.1.31

image

Question 2.32

titanicsample

32. Relative frequency bar graph of survived.

Question 2.33

titanicsample

33. Frequency bar graph of class.

2.1.33

image

Question 2.34

titanicsample

34. Relative frequency bar graph of class.

Question 2.35

titanicsample

35. Pie chart for survived.

2.1.35

image

Question 2.36

titanicsample

36. Pie chart for class.

Question 2.37

titanicsample

37. Crosstabulation of the variables gender and class.

2.1.37

1st 2nd 3rd Crew Total
Female 1 1 2 0 4
Male 1 3 3 9 16
Total 2 4 5 9 20

Use the crosstabulation in Exercise 37 for Exercises 38–41.

Question 2.38

titanicsample

38. For which categories of class did females outnumber males?

Question 2.39

titanicsample

39. For which category of class did males most outnumber females? Explain how this might make sense.

2.1.39

Crew. In 1912 women did not work as crew members on a ship. Only the people who could afford first class bought tickets for both men and women.

Question 2.40

titanicsample

40. For which category of class did the number of females come closest to the number of males?

Question 2.41

titanicsample

41. Build a crosstabulation of the variables gender and survived.

2.1.41

No Yes Total
Female 1 3 4
Male 10 6 16
Total 11 9 20

Use the crosstabulation in Exercise 41 for Exercises 42–45.

Question 2.42

titanicsample

42. What is the proportion of females who survived?

Question 2.43

titanicsample

43. Find the proportion of males who survived.

2.1.43

0.375

Question 2.44

titanicsample

44. It turns out that a greater proportion of females survived than males. Would we have been able to uncover this fact using only frequency distributions of the variables gender and survived, and not using a crosstabulation? Explain.

Question 2.45

titanicsample

45. Construct a crosstabulation of the variables class and survived.

2.1.45

No Yes Total
1st 0 2 2
2nd 2 2 4
3rd 2 3 5
Crew 7 2 9
Total 11 9 20

Use the crosstabulation in Exercise 45 for Exercises 46–48.

Question 2.46

titanicsample

46. What is the proportion of 1st class passengers who survived?

Question 2.47

titanicsample

47. Find the proportion of 2nd class passengers, 3rd class passengers, and crew who survived.

2.1.47

0.5, 0.6, 0.22

Question 2.48

titanicsample

48. Compare the proportions you found in the previous two exercises, and comment on the results.

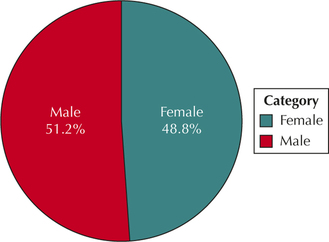
Table 14 shows the number of injuries in various winter sports to occur to females and males at the 2010 Winter Olympics.2 Use Table 14 to construct the graph or distribution indicated in Exercises 49–52, for the number of alpine skiing injuries, for female and male athletes.

Question 2.49

49. Frequency distribution

2.1.49

Gender Frequency
Female 20
Male 21

Question 2.50

50. Relative frequency distribution

Question 2.51

51. Pie chart

2.1.51

image

Question 2.52

52. Relative frequency bar graph

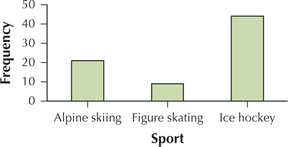
Use Table 14 to construct the graph or distribution indicated in Exercises 53–56, for the number of Olympic injuries, for male athletes only.

Question 2.53

53. Frequency distribution

2.1.53

Sport Frequency
Alpine skiing 21
Figure skating 9
Ice hockey 44

Question 2.54

54. Relative frequency distribution

Question 2.55

55. Frequency bar graph

2.1.55

image

Question 2.56

winterolympics

56. Relative frequency bar graph

55

Table 2.26: TABLE 14 Number of injuries suffered, by sport, at the 2010 Winter Olympics
Sport
Gender Alpine
skiing		 Figure
skating		 Ice
hockey		 Total
Female 20 12 38 70
Male 21 9 44 74
Total 41 21 82 144

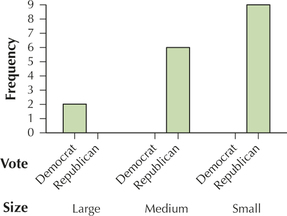
Question 2.57

57. Use Table 12 to produce a clustered bar graph of size, clustered by vote.

2.1.57

image

Use Table 13 to produce clustered bar graphs for the variables indicated in Exercises 58–60.

Question 2.58

58. Clustered bar graph of gender, clustered by survived

Question 2.59

59. Clustered bar graph of class, clustered by survived

2.1.59

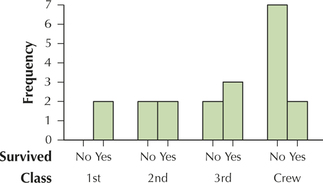
image

Question 2.60

60. Clustered bar graph of survived, clustered by gender

APPLYING THE CONCEPTS

World Water Usage. See Table 15 for Exercises 61–64. For the indicated variable, construct the following:

  1. Frequency distribution
  2. Relative frequency distribution
  3. Frequency bar graph
  4. Relative frequency bar graph
  5. Pareto chart, using relative frequencies
  6. Pie chart
Table 2.27: TABLE 15 World water usage
Country Continent Climate Main use
Iraq Asia Arid Irrigation
United States North America Temperate Industry
Pakistan Asia Arid Irrigation
Canada North America Temperate Industry
Madagascar Africa Tropical Irrigation
North Korea Asia Temperate Not reported
Chile South America Arid Irrigation
Bulgaria Europe Temperate Not reported
Afghanistan Asia Arid Irrigation
Iran Asia Arid Irrigation

Question 2.61

worldwater

61. The variable continent

2.1.61

(a)–(b)

Continent Frequency Relative frequency
Africa 1 0.10
Asia 5 0.50
Europe 1 0.10
North America 2 0.20
South America 1 0.10

(c)

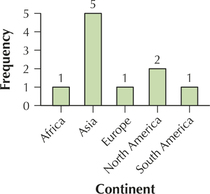
image

(d)

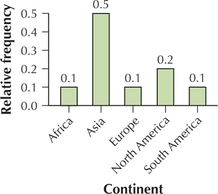
image

(e)

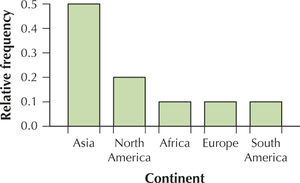
image

(f)

image

Question 2.62

worldwater

62. The variable climate

Question 2.63

worldwater

63. The variable main use

2.1.63

(a)–(b)

Main use Frequency Relative frequency
Industry 2 0.20
Irrigation 6 0.60
Not reported 2 0.20

(c)

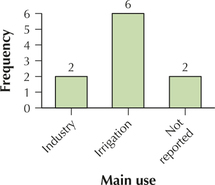
image

(d)

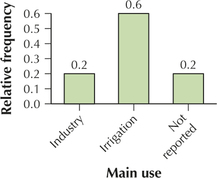
image

(e)

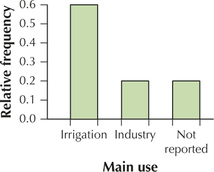
image

(f)

image

Question 2.64

worldwater

64. Explain why it is not appropriate to construct a frequency distribution for country.

Use Table 15 for Exercises 65–70.

Question 2.65

65. Construct a crosstabulation of the variables continent and climate.

2.1.65

Arid Temperate Tropical Total
Africa 0 0 1 1
Asia 4 1 0 5
Europe 0 1 0 1
North America 0 2 0 2
South America 1 0 0 1
Total 5 4 1 10

Question 2.66

66. Construct a crosstabulation of the variables continent and main use.

Question 2.67

67. Construct a crosstabulation of the variables climate and main use.

2.1.67

Industry Irrigation Not reported Total
Arid 0 5 0 5
Temperate 2 0 2 4
Tropical 0 1 0 1
Total 2 6 2 10

Question 2.68

68. Construct a clustered bar graph of the variable continent clustered by climate.

Question 2.69

69. Construct a clustered bar graph of the variable main use clustered by continent.

2.1.69

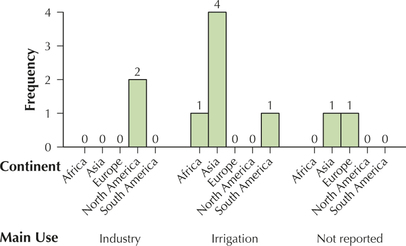
image

Question 2.70

70. Construct a clustered bar graph of the variable main use clustered by climate.

Video Game Sales. Open the VideoGameSales data set that we used for the Chapter 1 Case Study. See Table 3 on page 8 in Chapter 1. Recall that this data set contains the top 30 best-selling video games in the United States for the week of May 17, 2014, along with the game platform, publishing studio, type of game, sales that week, total sales, and how many weeks the game has been on the list. Use the data set to answer Exercises 71–76.

Question 2.71

videogamesales

71. Construct a frequency distribution and a relative frequency distribution for the variable type. Which is the most common game type? The least common?

2.1.71

image

Question 2.72

videogamesales

72. Build a frequency bar graph of the variable platform. Which is the most popular platform?

Question 2.73

videogamesales

73. Make a relative frequency bar graph of the variable platform. What percentage of platforms is the PS4?

2.1.73

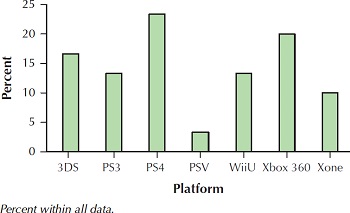
image

23%

Question 2.74

videogamesales

74. Construct a pie chart for the variable type.

Question 2.75

videogamesales

75. Build a crosstabulation of type and platform.

2.1.75

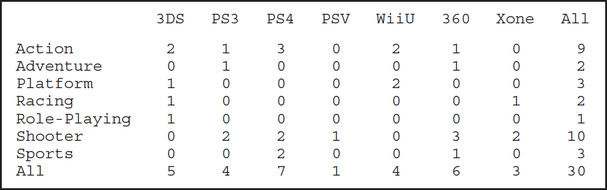
image

Question 2.76

videogamesales

76. Refer to the crosstabulation. Which platform has the most action games? The most shooter games?

Cell Phone Ownership. Figure 14 shows the percentage of cell phone ownership categorized by level of education.3 Use Figure 14 to answer Exercises 77 and 78.

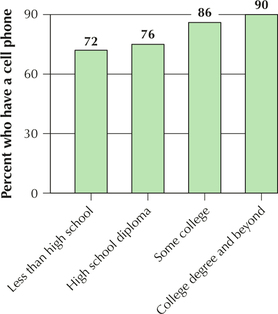
image
Figure 2.14: FIGURE 14 Cell phone ownership.

Question 2.77

77. Can we use the information in Figure 14 to construct a pie chart? Explain why or why not.

2.1.77

No. There are actually two categorical variables—level of education and whether or not the person owns a cell phone. The percents are percents of each category of level of education who own cell phones and not the percent of the whole group who own cell phones.

Question 2.78

78. Is Figure 14 a Pareto chart? Explain why or why not.

Cell Phones and the Internet. Figure 15 is a pie chart representing the percentage of Americans who access the Internet or email using their cell phones. Use Figure 15 to answer Exercises 79 and 80.

Question 2.79

79. According to this survey:

  1. What is the most common response? What percentage does this represent?
  2. What is the least common response? What percentage does this represent?

    56

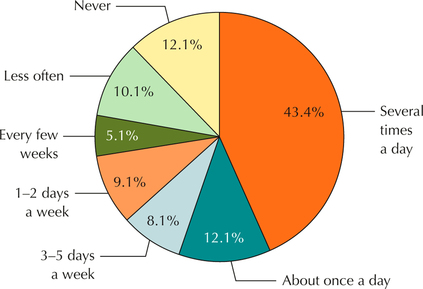    image
    Figure 2.15: FIGURE 15 Percentage using cell phones for Internet or email.4

2.1.79

(a) Several times a day; 43.4% (b) Every few weeks; 5.1%

Question 2.80

80. According to this survey:

  1. What percentage uses the cell phone to access the Internet or email about once a day?
  2. What percentage never uses the cell phone to access the Internet or email?
  3. If 1000 adults were surveyed, how many never use their cell phones for email or Internet?

Sledding injuries. Every year, about 20,000 children and teenagers visit the emergency room with injuries sustained from snow sledding.5 Use the horizontal bar graph in Figure 16 to answer Exercises 81 and 82.

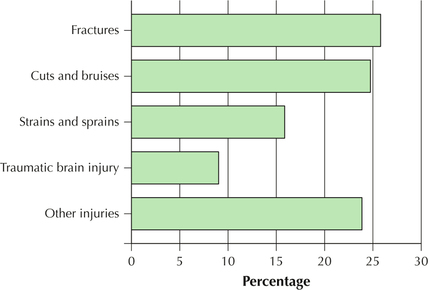
image
Figure 2.16: FIGURE 16 Most common injuries from sledding.

Question 2.81

81. According to this study:

  1. What is the most common category of injury? Estimate the percentage.
  2. Of the specific injuries shown, what is the least common category of injury? What is the percentage?
  3. Is it possible for there to be an injury type that has a lower percentage than traumatic brain injury? Explain.

2.1.81

(a) Fractures; 26% (b) Traumatic brain injury; 9% (c) Yes. It would have to be one of the injuries included in the category “Other injuries.”

Question 2.82

82. According to this study:

  1. What is the percentage for cuts and bruises?
  2. What is the percentage for strains and sprains?

Question 2.83

cartypemodel

83. Table 16 shows the numbers of vehicle models, which are categorized by vehicle type, examined each year by the U.S. Department of Energy to determine vehicle gas mileage. Use Table 16 to construct the following:

  1. Relative frequency distribution
  2. Frequency bar graph
  3. Relative frequency bar graph
  4. Pareto chart, using relative frequencies
  5. Pie chart of the relative frequencies
Table 2.32: TABLE 16 Frequency distribution of vehicle type
Vehicle type Number of models
SUVs 370
Compact cars 128
Midsize cars 120
Subcompact cars 110
Standard pickup trucks 106
Large cars 76
Station wagons 62
Small pickup trucks 59
Other types 151
Total 1182

2.1.83

(a) Relative frequency distribution of vehicle type

Vehicle type Relative frequency
SUVs 0.3130
Compact cars 0.1083
Midsize cars 0.1015
Subcompact cars 0.0931
Standard pickup trucks 0.0897
Large cars 0.0643
Station wagons 0.0525
Small pickup trucks 0.0499
Other types 0.1277
Total 1.0000

(b)

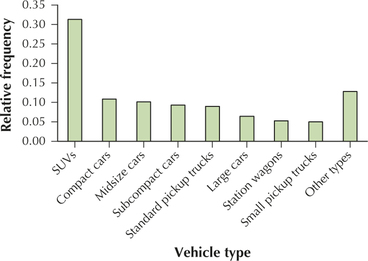
image

(c)

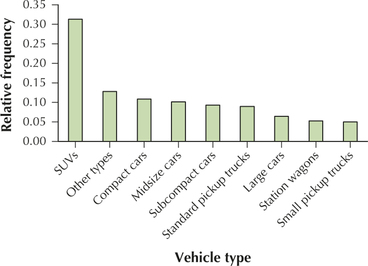
image

(d)

image

(e)

image

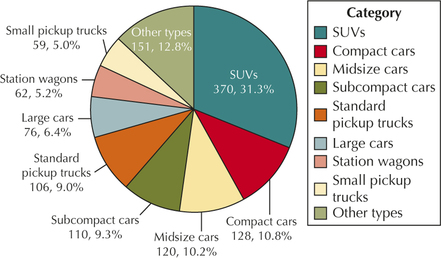
Musical activities. Use the following information for Exercises 84 and 85. USA Weekend conducted a survey of the nation's teenagers, asking them various questions about lifestyle and music. Nearly 60,000 teenagers responded to the poll, which was conducted in part through USA Weekend's Web site. One question was, “Do you listen to music while you are … ?” and listed several options. Respondents were asked to select all that apply. The most common responses are shown in the table below.

Doing chores 79%
On the computer 73%
Doing homework 72%
Eating meals at home 33%
In the classroom 18%

Question 2.84

84. Do you think that the sample is representative of all U.S. teenagers? How might the sample systematically introduce bias?

Question 2.85

85. Can you construct a pie chart of the five activities listed in the table? Explain precisely why or why not.

2.1.85

A pie chart cannot be constructed for the data since the percentages for the different classes do not add up to 100%. Respondents could select more than one category.

Music and Violence. Another poll question asked by USA Weekend was “Do you think shock rock and gangsta rap are partly to blame for violence such as school shootings or physical abuse?” The results are shown in the table below. Use this information to answer Exercises 86–89.

57

Yes 31%
No 45%
I've never thought about it 24%

Question 2.86

86. Assuming the sample size is 6000, construct a frequency distribution of the responses.

Question 2.87

87. Make a relative frequency distribution of the responses.

2.1.87

Response Relative frequency
Yes 0.31
No 0.45
I've never thought about it 0.24

Question 2.88

88. Construct a frequency bar graph of the responses.

Question 2.89

89. Construct a relative frequency pie chart of the responses.

2.1.89

Relative frequencies are expressed as percentages.

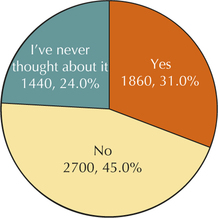
image

Astrological Signs. Use the following information for Exercises 90–92. The General Social Survey collects data on social aspects of life in America. Here, 1464 respondents reported their astrological signs. A pie chart of the results is shown below.

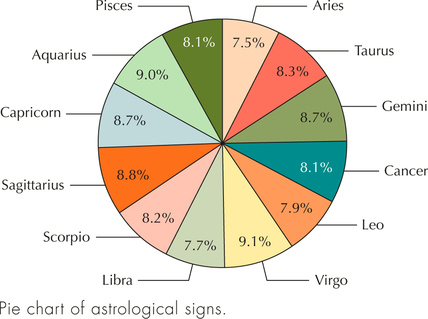
image
Pie chart of astrological signs.

Question 2.90

90. Answer the following:

  1. What is the most common astrological sign?
  2. What is the least common astrological sign?

Question 2.91

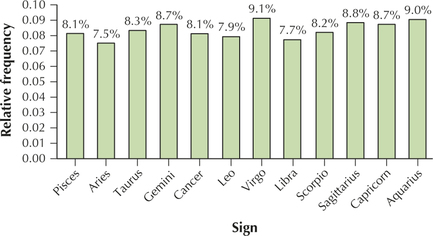
91. Use the percentages in the pie chart to do the following:

  1. Construct a relative frequency bar graph of the astrological signs.
  2. Construct a relative frequency bar graph, but, this time, have the y axis begin at 7% instead of zero. Describe the difference between the two bar graphs. When would this one be used as opposed to the earlier bar graph?

2.1.91

(a)

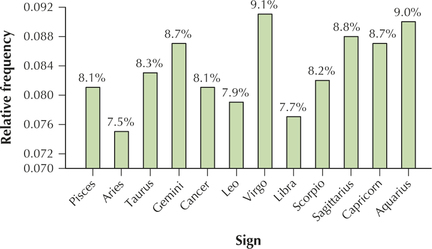
image

(b)

image

The graph in (b) uses an adjusted scale, which is misleading. Use this graph to magnify the small variability in percentages.

Question 2.92

92. Construct a frequency distribution of the astrological signs. Which sign occurs the least? The most?

Satisfaction with Family life. Use the following information for Exercises 93–95. The General Social Survey also asked respondents about their amount of satisfaction with family life. Here, 1002 respondents reported their satisfaction levels with family life, as shown in the frequency distribution below.

Satisfaction Frequency
Very great deal 415
Great deal 329
Quite a bit 99
A fair amount 90
Some 27
A little 25
None 17
Total 1002

Question 2.93

satisfaction

93. Construct a Pareto graph of the categories. Do you think that, overall, people are happy with their family lives?

2.1.93

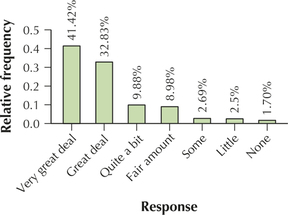
image

Categories are qualitative; interpretation will vary.

Question 2.94

satisfaction

94. Construct a frequency or a relative frequency bar graph of the categories. Do you think that this bar graph reinforces the positive message in the data?

Question 2.95

satisfaction

95. What is your opinion of the categories? Do you think that everyone interprets these phrases in the same way? For example, what is the difference between “quite a bit” and “great deal”?

2.1.95

No.

Litter. Don't Mess with Texas (http://dontmesswithtexas.org) is a Texas statewide anti-littering organization that identified paper, plastic, metals, and glass as the top four categories of litter by composition. The report also identified tobacco, household, food, and beverages as the top four categories of litter by use. A sample of 12 items of litter had the following characteristics. Use the table to answer Exercises 96–98.

Litter item Composition Use
1 Paper Tobacco
2 Plastic Household
3 Glass Beverages
4 Paper Tobacco
5 Metal Household
6 Plastic Food
7 Glass Beverages
8 Paper Household
9 Metal Household
10 Plastic Beverages
11 Paper Tobacco
12 Plastic Food

Question 2.96

litter

96. Construct a crosstabulation of litter composition by litter use.

Question 2.97

litter

97. Construct a clustered bar graph of litter composition and litter use. Cluster by use.

2.1.97

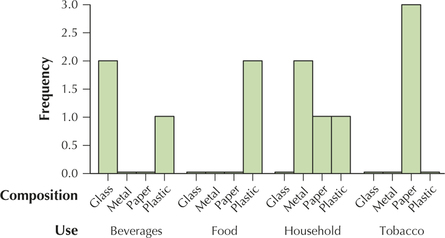
image

Question 2.98

litter

98. Identify any patterns you discover.

image Misdemeanors in New York City.

For Exercises 99–101, refer to Figure 17, a bar chart of the total number of misdemeanor crimes committed in New York City in 2013 categorized by misdemeanor type.

Question 2.99

99. Which category leads all categories of misdemeanor crime in New York City?

2.1.99

Petit larceny

Question 2.100

100. About how many petit larceny cases were there in 2013?

Question 2.101

101. Is Figure 17 in the form of a Pareto graph? Explain why or why not.

2.1.101

Yes. The categories are arranged in order from highest frequency to lowest frequency.

58

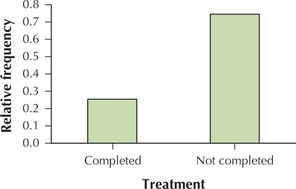
image
Figure 2.17: FIGURE 17 Bar chart of misdemeanors in New York City.

Comparison Pie Chart. The Centers for Disease Control and Prevention (CDC) recommends routine vaccination with Gardasil for boys and girls ages 11 and 12, in order to combat the HPV virus. For example, it has been shown that 99.7% of cervical cancer patients have been infected with the HPV virus.6 The large data set Gardasil (Source: Journal of Statistics Education)7 contains information regarding 1414 young women who underwent vaccination treatment. To complete the vaccination, a series of three shots must be undertaken. Researchers were interested in whether the location of the clinic was related to the proportion of patients who completed treatment. Figure 18 shows a comparison pie chart—a pair of pie charts of the proportion of patients completing the vaccine treatment, with one pie chart for suburban locations and one pie chart for urban locations.

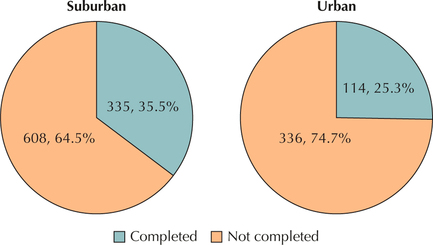
image
Figure 2.18: FIGURE 18 Comparison pie chart of treatment completion proportions.

Question 2.102

102. What proportion of females from suburban locations completed the treatment? From urban locations?

Question 2.103

103. Use the data from the comparison pie chart to make the following relative frequency bar charts.

  1. Treatment status for suburban females
  2. Treatment status for urban females

2.1.103

(a)

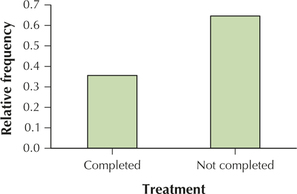
image

(b)

image

Question 2.104

104. Do you think that the 35.5% to 25.3% difference in vaccine completion is just due to chance, or do you think that it represents a real disparity between the two groups?

BRINGING IT ALL TOGETHER

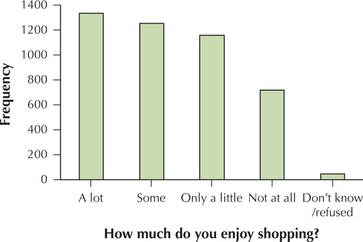
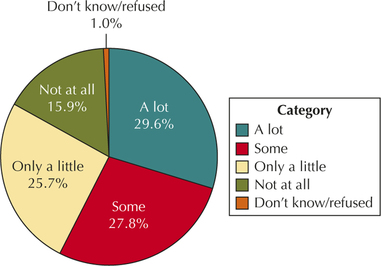
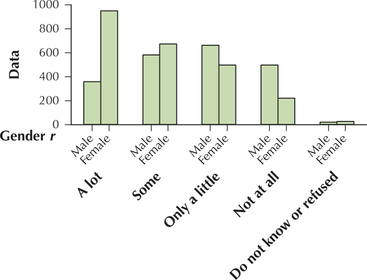
Shopping Enjoyment and Gender. Use the information in the crosstabulation for Exercises 105–119. The Pew Internet and American Life Project surveyed 4514 American men and women and asked them, “How much, if at all, do you enjoy shopping?” The results shown in the crosstabulation are missing some entries.

Gender
Male Female Total
A lot — 950 1338
Some 582 — 1255
Only a little 662 497 —
Not at all 497 — 717
Don't know/refused — 25 45
Total 2149 4514
Table 2.39: Crosstabulation of shopping enjoyment by gender

Question 2.105

105. Fill in the missing entries.

2.1.105

Missing values are in red

“How much do you enjoy shopping?” Gender Total
Male Female
A lot 388 950 1338
Some 582 673 1255
Only a little 662 497 1159
Not at all 497 220 717
Don't know/refused 20 25 45
Total 2149 2365 4514

Question 2.106

106. Convert the table to a relative frequency crosstabulation. Make it so that the “Male” and “Female” proportions in each row add up to 1.0.

Question 2.107

107. Did men or women have the higher proportion of respondents who enjoy shopping

  1. a lot?
  2. some?
  3. only a little?
  4. not at all?

2.1.107

(a) Women (b) Women (c) Men (d) Men

59

Question 2.108

108. Construct a frequency distribution of gender.

Question 2.109

109. Build a frequency distribution of response.

2.1.109

How much do you enjoy shopping? Frequency
A lot 1338
Some 1255
Only a little 1159
Not at all 717
Don't know 45

Question 2.110

110. Make a relative frequency distribution of gender.

Question 2.111

111. Construct a relative frequency distribution of response.

2.1.111

How much do you enjoy shopping? Relative frequency
A lot 0.2964
Some 0.2780
Only a little 0.2568
Not at all 0.1588
Don't know 0.0100

Question 2.112

112. Build a bar graph of gender.

Question 2.113

113. Make a bar graph of response.

2.1.113

image

Question 2.114

114. Construct a pie chart of gender.

Question 2.115

115. Build a pie chart of response.

2.1.115

image

Question 2.116

116. Construct a clustered bar graph of gender clustered by response.

Question 2.117

117. Build a clustered bar graph of response clustered by gender.

2.1.117

image

Question 2.118

118. What proportion of the respondents is female?

Question 2.119

image 119. What if we doubled each cell count? How would that affect the following?

  1. Frequency distribution of gender
  2. Relative frequency of gender
  3. Pie chart of gender

2.1.119

(a) Frequencies would double (b) Stay the same (c) Stay the same

WORKING WITH LARGE DATA SETS

Educational Goals in Sports. Use your knowledge of technology to solve Exercises 120 and 121. Open the Goals data set. The subjects are students in grades four, five, and six from three school districts in Michigan. The students were asked which of the following was most important to them: good grades, sports, or popularity. Information about the students' ages, genders, races, and grades was also gathered, as well as whether their schools were in an urban, suburban, or rural setting.8

Question 2.120

goals

120. Generate bar graphs for the following variables.

  1. Gender. Estimate the relative frequency of girls, and boys, in the sample.
  2. Goals. About what percentage of the students chose “grades” as most important? About what percentage chose “popular”? About what percentage chose “sports”?

Question 2.121

goals

121. Generate relative frequency distributions for the following variables.

  1. Gender. How close were your estimates in the previous exercise?
  2. Goals. How close were your estimates in the previous exercise?

2.1.121

(a)

image

(b)

image

WORKING WITH LARGE DATA SETS

Analysis of Households. For Exercises 122–124, use your knowledge of technology. Open the data set household.

Question 2.122

household

122. How many observations are in this data set? How many variables?

Question 2.123

household

123. Which of the variables are qualitative? Which of the variables are quantitative?

2.1.123

Qualitative: State; Quantitative: Tot_hhld, Fam_tpc, Fam_mpc, Fam_fpc, Nfm_tpc, Nfm_lpc, and Ave_size.

Question 2.124

household

124. What would a relative frequency distribution of the variable state look like? A pie chart? A bar graph?

WORKING WITH LARGE DATA SETS

Open the data set Titanic. Use technology for Exercises 125–130.

Question 2.125

titanic

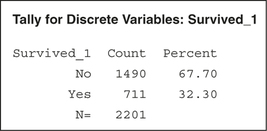
125. Construct (i) a frequency distribution and (ii) a relative frequency distribution of each of the following variables:

  1. Class
  2. Age
  3. Sex
  4. Survived

2.1.125

(a)

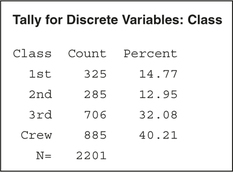
image

(b)

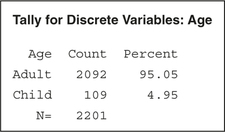
image

(c)

image

(d)

image

Question 2.126

titanic

126. Build (i) a frequency bar graph and (ii) a relative frequency bar graph of each of the following variables:

  1. Class
  2. Age
  3. Sex
  4. Survived

Question 2.127

titanic

127. Construct pie charts of each variable in the previous exercise.

2.1.127

(a)

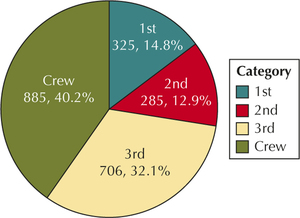
image

(b)

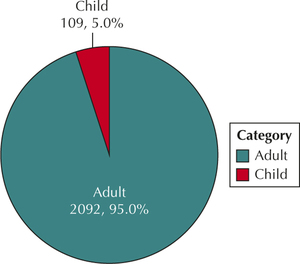
image

(c)

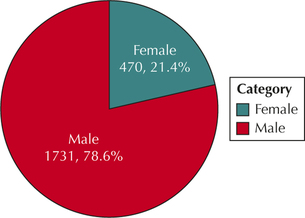
image

(d)

image

Question 2.128

titanic

128. Construct a clustered bar graph of the variable survived clustered by gender. What does this graph tell us about the relative proportions of females and males who survived?

Question 2.129

titanic

129. Construct a clustered bar graph of the variable survived clustered by age. Did you stand a better chance of surviving as an adult or a child?

2.1.129

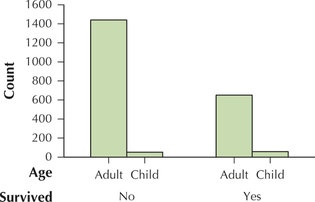
image

A child.

Question 2.130

titanic

130. Construct a clustered bar graph of the variable survived clustered by class. Which class had the best chance of surviving? (Hint: For each class, compare the heights of the “Yes” rectangles to the heights of the “No” rectangles.)

CONSTRUCT YOUR OWN DATA SETS

Environmental Club. Use the following information for Exercises 131–133. You are the president of the College Environmental Club, which has members among all four classes: freshmen, sophomores, juniors, and seniors. The total number of members in the club is 20.

Question 2.131

131. Set the frequency of each class so that each class has an equal number of members.

  1. Construct a frequency distribution of the variable class.
  2. Construct a relative frequency distribution of the variable class.

2.1.131

(a) and (b)

Class Frequency Relative frequency
Freshman 5 0.25
Sophomore 5 0.25
Junior 5 0.25
Senior 5 0.25

Question 2.132

132. Set the frequency of each class so that there are more sophomores than freshmen, more juniors than sophomores, and more seniors than juniors.

  1. Construct a Pareto chart of the variable class.
  2. Construct a pie chart of the variable class.

Question 2.133

133. Set the frequency of each class so that there are more seniors than any other class, while the other three classes have equal numbers.

  1. Construct a frequency bar graph of the variable class.
  2. Construct a relative frequency bar graph of the variable class.

2.1.133

Answers will vary.

petitlarceny

WORKING WITH LARGE DATA SETS

image Open the data set Petit larceny, which contains the number of petit larceny misdemeanors, per precinct, for the years 2000–2013. For the years 2000 and 2013, these frequencies have been categorized into four categories: 1 – Low: 800 or less, 2 – Medium: 800 to less than 1050, 3 – High: 1050 to less than 1500, and 4 – Very High: 1500 or more. Use technology to answer the following:

60

Question 2.134

petitlarceny

134. Construct bar graphs of “2000 categorized” and “2013 categorized.”

Question 2.135

petitlarceny

135. Discuss the differences between the bar graphs. Which categories are larger or smaller? On the whole, do you think this represents good news or bad news?

2.1.135

In 2000 there were more precincts that had category 3 and 4 numbers of petit larcenies than in 2013. In 2000 there were fewer precincts that had category 1 and 2 numbers of petit larcenies than in 2013. Good news.

Question 2.136

petitlarceny

136. Construct pie charts of “2000 categorized” and “2013 categorized.”

Question 2.137

petitlarceny

137. Discuss whether the bar graphs or the pie charts express the results more clearly in this case.

2.1.137

Pie charts, since they show each category as a percent of the whole.