Section 6.4Exercises

CLARIFYING THE CONCEPTS

Question 6.215

1. For a continuous random variable , why are we not interested in whether equals some particular value? (p. 349)

6.4.1

The probability that X equals some particular value is zero.

Question 6.216

2. In the graph of a probability distribution, what is represented on the number line? (p. 349)

Question 6.217

3. How is probability represented in the graph of a continuous probability distribution? (p. 350)

6.4.3

Area under the normal distribution curve above an interval.

Question 6.218

4. What are the possible values for the mean of a normal distribution? For the standard deviation? (p. 352)

Question 6.219

5. True or false: The graph of the uniform distribution is always shaped like a square. (p. 350)

6.4.5

False

Question 6.220

6. For continuous probability distributions, what is the difference between and ? (p. 351)

Question 6.221

7. What is the value for the mean of the standard normal distribution? (p. 354)

6.4.7

0

Question 6.222

8. What is the value for the standard deviation of the standard normal distribution? (p. 354)

Question 6.223

9. True or false: The area under the curve to the right of is 0.5. (p. 354)

6.4.9

True

Question 6.224

10. True or false: . (p. 349)

PRACTICING THE TECHNIQUES

image CHECK IT OUT!

To do Check out Topic
Exercises
11–20		 Example 25 Uniform probability
distribution
Exercises
21–30		 Example 26 Normal distribution mean and
standard deviation
Exercises
31–36		 Example 27 Properties of the normal curve
Exercises
37–44		 Example 28 Find the area to left of the

-value
Exercises
45–48		 Example 29 Find the area to right of the

-value
Exercises
49–58		 Example 30 Find the area between two

-value
Exercises
59–70		 Example 32 Expressing areas under the
standard normal curve as
probabilities
Exercises
71–78		 Example 33 Finding the -value, given
area to its left
Exercises
79–86		 Example 34 Finding the -value, given
area to its right
Exercises
87–90		 Example 35 Find two that mark
the boundaries of the middle
95% of the area

For Exercises 11–16, assume that is a uniform random variable, with left endpoint 0 and right endpoint 100. Find the following probabilities:

Question 6.225

11.

6.4.11

0.5

Question 6.226

12.

Question 6.227

13.

6.4.13

0.65

Question 6.228

14.

Question 6.229

15.

6.4.15

0.01

Question 6.230

16.

364

For Exercises 17–20, assume that is a uniform random variable, with left endpoint −5 and right endpoint 5. Compute the following probabilities:

Question 6.231

17.

6.4.17

0.5

Question 6.232

18.

Question 6.233

19.

6.4.19

0.1

Question 6.234

20.

Question 6.235

21. The two normal distributions in the accompanying figure have the same standard deviation of 5 but different means. Which normal distribution has mean 10 and which has mean 25? Explain how you know this.

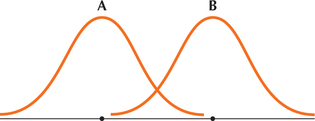
image

6.4.21

A has mean 10; B has mean 25. The peak of a normal curve is at the mean; from the graphs we see that the mean of A is less than the mean of B.

Question 6.236

22. The two normal distributions in the figure below have the same mean of 100 but different standard deviations. Which normal distribution has standard deviation 3 and which has standard deviation 6? Explain how you know this.

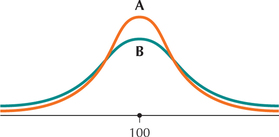
image

For Exercises 23–30, use the graph of the normal distribution to determine the mean and standard deviation. (Hint: The distance between dotted lines in the figures represents 1 standard deviation.)

Question 6.237

23.

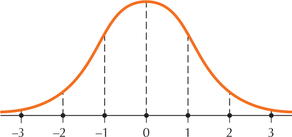
image

6.4.23

,

Question 6.238

24.

image

Question 6.239

25.

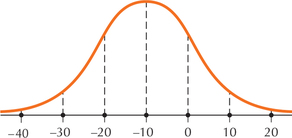
image

6.4.25

,

Question 6.240

26.

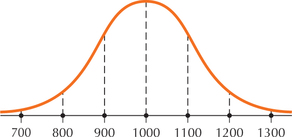
image

Question 6.241

27.

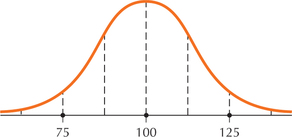
image

6.4.27

,

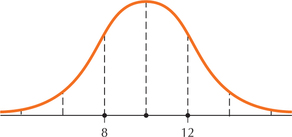
Question 6.242

28.

image

Question 6.243

29.

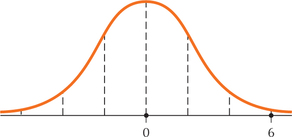
image

6.4.29

,

Question 6.244

30.

image

Use the normal distribution from Example 27 for Exercises 31–36. Birth weights are normally distributed with a mean weight of and a standard deviation of .

Question 6.245

31. What is the probability of a birth weight equal to 3285 grams?

6.4.31

0

Question 6.246

32. What is the probability of a birth weight more than 3285 grams?

Question 6.247

33. What is the probability of a birth weight of at least 3285 grams?

6.4.33

0.5

Question 6.248

34. What can we say about the area to the left of 3285 grams and the area to the right of 3285 grams?

Question 6.249

35. Is the area to the right of greater than or less than 0.5? How do you know this?

6.4.35

Less than 0.5. Since is greater than the mean of 3285 and the area to the right of is 0.5, the area to the right of is less than the area to the right of .

Question 6.250

36. Is the area to the left of greater than or less than 0.5? How do you know this?

365

For Exercises 37–58,

  1. draw the graph.
  2. find the area using the table or technology.

Find the area under the standard normal curve that lies to the left of the following:

Question 6.251

37.

6.4.37

(a)

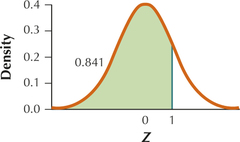
image

(b) 0.8143

Question 6.252

38.

Question 6.253

39.

6.4.39

(a)

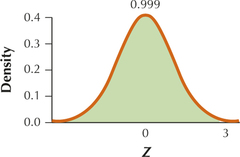
image

(b) 0.9987

Question 6.254

40.

Question 6.255

41.

6.4.41

(a)

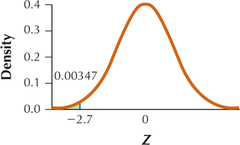
image

(b) 0.0035

Question 6.256

42.

Question 6.257

43.

6.4.43

(a)

image

(b) 0.4207

Question 6.258

44.

Find the area under the standard normal curve that lies to the right of the following:

Question 6.259

45.

6.4.45

(a)

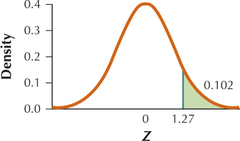
image

(b) 0.1020

Question 6.260

46.

Question 6.261

47.

6.4.47

(a)

image

(b) 0.9987

Question 6.262

48.

Find the area under the standard normal curve that lies between the following:

Question 6.263

49. and

6.4.49

(a)

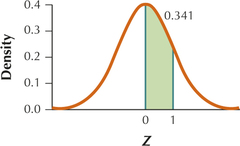
image

(b) 0.3413

Question 6.264

50. and

Question 6.265

51. and

6.4.51

(a)

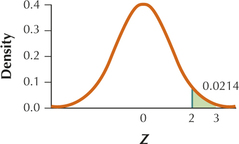
image

(b) 0.0214

Question 6.266

52. and

Question 6.267

53. and

6.4.53

(a)

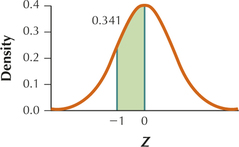
image

(b) 0.3413

Question 6.268

54. and

Question 6.269

55. and

6.4.55

(a)

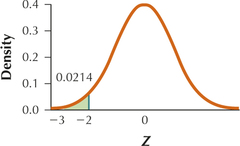
image

(b) 0.0214

Question 6.270

56. and

Question 6.271

57. and

6.4.57

(a)

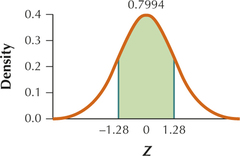
image

(b) 0.7994

Question 6.272

58. and

For Exercises 59–70, find the indicated probability for the standard normal .

  1. Draw the graph.
  2. Find the area using the table or technology.

Question 6.273

59.

6.4.59

(a)

image

(b) 0

Question 6.274

60.

Question 6.275

61.

6.4.61

(a)

image

(b) 1

Question 6.276

62.

Question 6.277

63.

6.4.63

(a)

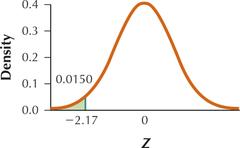
image

(b) 0.0150

Question 6.278

64.

Question 6.279

65.

6.4.65

(a)

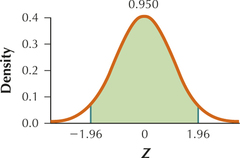
image

(b) 0.9500

Question 6.280

66.

Question 6.281

67.

6.4.67

(a)

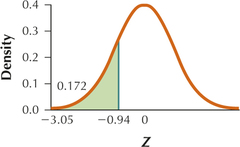
image

(b) 0.1725

Question 6.282

68.

Question 6.283

69.

6.4.69

(a)

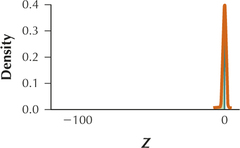
image

(b) 0.5000

Question 6.284

70.

For Exercises 71–78, find the -value with the following areas under the standard normal curve to its left. Draw the graph, and then find the -value.

Question 6.285

71. 0.3336

6.4.71

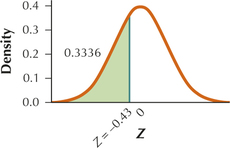
image

Question 6.286

72. 0.4602

Question 6.287

73. 0.3264

6.4.73

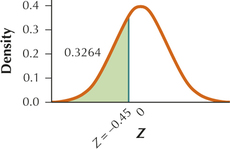
image

Question 6.288

74. 0.4247

Question 6.289

75. 0.95

6.4.75

1.65 (TI-83/84: 1.645)

image

Question 6.290

76. 0.975

Question 6.291

77. 0.98

6.4.77

2.05

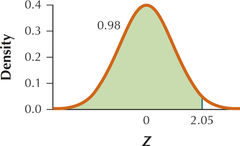
image

Question 6.292

78. 0.99

For Exercises 79–86, find the -value with the following areas under the standard normal curve to its right. Draw the graph, and then find the -value.

Question 6.293

79. 0.8078

6.4.79

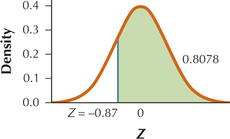
image

Question 6.294

80. 0.3085

Question 6.295

81. 0.9788

6.4.81

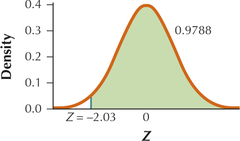
image

Question 6.296

82. 0.5120

Question 6.297

83. 0.90

6.4.83

𢄒1.28>

image

Question 6.298

84. 0.975

Question 6.299

85. 0.9988

6.4.85

−3.036 (Using the table, both −3.03 and −3.04 have area to the left of them equal to 0.0012 and area to the right of them as 0.9988.)

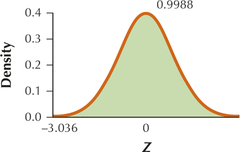
image

Question 6.300

86. 0.9998

For Exercises 87–94, find the values of that mark the boundaries of the indicated areas.

Question 6.301

87. The middle 80%

6.4.87

−1.28 and 1.28

Question 6.302

88. The middle 95%

Question 6.303

89. The middle 98%

6.4.89

−2.33 and 2.33

Question 6.304

90. The middle 85%

Question 6.305

91. Find the 50th percentile of the distribution. (Hint: See margin note on page 360.)

6.4.91

Question 6.306

92. Find the 75th percentile of the distribution.

Question 6.307

93. Find the value of that is larger than 99.5% of all values of .

6.4.93

Question 6.308

94. Find the value of that is smaller than 99.5% of all values of .

APPLYING THE CONCEPTS

Question 6.309

95. Uniform Distribution: Web Page Loading Time.

Suppose that the Web page loading time for a particular home network is uniform, with left endpoint 1 second and right endpoint 5 seconds.

  1. What is the probability that a randomly selected Web page will take between 3 seconds and 4 seconds to load?
  2. Find the probability that a randomly selected Web page will take between 1 second and 2 seconds to load.
  3. How often does it take less than 1 second for a Web page to load?
  4. What is the probability that it takes exactly 2 seconds for a page to load? Explain.

6.4.95

(a) 0.25 (b) 0.25 (c) 0 (d) 0. Area underneath the curve for a single value of is the area of a line that is 0.

Question 6.310

96. Uniform Distribution: Random Number Generation.

Computers and calculators use the uniform distribution to generate random numbers. Suppose we have a calculator that randomly generates numbers between 0 and 1, so that they form a uniform distribution.

  1. What is the probability that the random number generated is less than 0.3?
  2. Find the probability that a random number is generated that is between 0.27 and 0.92.

  3. What is the probability that a random number greater than 1 is generated?

    366

  4. What is the probability that the exact number 0.5 is generated? Explain.

For Exercises 97–100, sketch the distribution, showing , and .

Question 6.311

97. Windy Frisco. The average wind speed in San Francisco in July is 13.6 miles per hour (mph), according to the U.S. National Oceanic and Atmospheric Administration. Suppose that the distribution of the wind speed in July in San Francisco is normal, with mean mph and standard deviation .

6.4.97

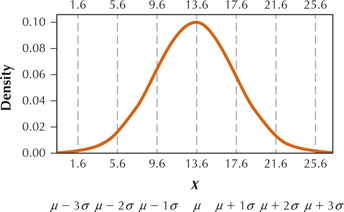
image

Question 6.312

98. Price of Crude Oil. The Organization of Petroleum Exporting States reports that the mean price for crude oil in July 2014 was $105.115 (one hundred five dollars, eleven and a half cents) per barrel. Assume the data is normal, with mean and standard deviation .

Question 6.313

99. Hospital Patient Length of Stays. A study of Pennsylvania hospitals showed that the mean patient length of stay was 4.87 days, with a standard deviation of 0.97 day.16 Assume that the distribution of patient length of stays is normal.

6.4.99

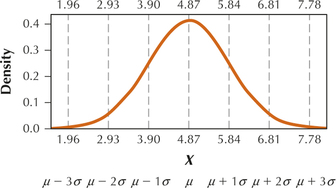
image

Question 6.314

100. Facebook Friends. Statistica reported in 2014 that the mean number of Facebook friends for 18- to 24-year-olds was 649. Assume the distribution is normal, with friends and standard deviation friends.

Question 6.315

101. Percentiles of the Uniform Distribution. The th percentile of a continuous distribution is the value of that is greater than or equal to % of the values of . Find the following percentiles of the uniform distribution in Example 25:

  1. 95th
  2. 90th
  3. 97.5th
  4. 5th
  5. 10th
  6. 2.5th

6.4.101

(a) 9.5 minutes (b) 9 minutes (c) 9.75 minutes (d) 0.5 minute (e) 1 minute (f) 0.25 minute

Question 6.316

102. Mean of the Uniform Distribution. Explain two ways that you could find the mean of the uniform distribution.

  1. Use the balance point method.
  2. Find the median (50th percentile), and argue that, because the distribution is rectangle-shaped, the mean equals the median.

For Exercises 103–114, use the graph of the standard normal distribution to find the shaded area using the table or technology.

Question 6.317

103.

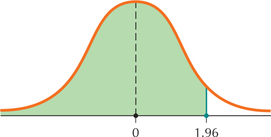
image

6.4.103

0.9750

Question 6.318

104.

image

Question 6.319

105.

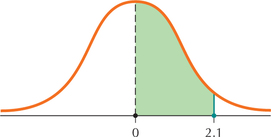
image

6.4.105

0.4821

Question 6.320

106.

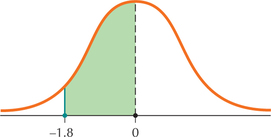
image

Question 6.321

107.

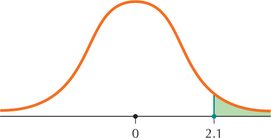
image

6.4.107

0.0179

Question 6.322

108.

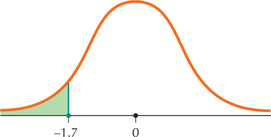
image

Question 6.323

109.

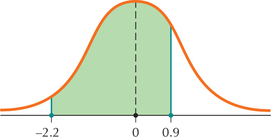
image

6.4.109

0.8020

Question 6.324

110.

image

Question 6.325

111.

image

6.4.111

0.1832

367

Question 6.326

112.

image

Question 6.327

113.

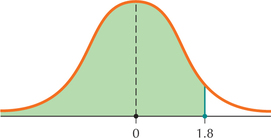
image

6.4.113

0.9641

Question 6.328

114.

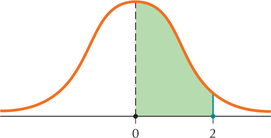
image

Question 6.329

115. Standardized Test Scores. Nicholas took a standardized test and was informed that the -value of his test score was 1.0. Find the percentages of test takers that Nicholas scored higher than.

6.4.115

0.8413

Question 6.330

116. Standardized Test Scores. Samantha's -value for her standardized test performance was 1.5. Calculate the proportion of test takers that Samantha scored higher than.

Question 6.331

117. High Jump. Brandon's score in the high jump at a track-and-field event showed that he was able to jump higher than 45% of the competitors. Find the -value for Brandon's high-jump score.

6.4.117

−0.13

Question 6.332

118. Body Temperature. The body temperatures of all the students in Kayla's class were measured. Kayla's body temperature was lower than 90% of her classmates. Find the -value corresponding to Kayla's body temperature.

Question 6.333

119. Checking the Empirical Rule. Check the accuracy of the Empirical Rule for . That is, find the area between and using the techniques of this section. Then compare your finding with the results for using the Empirical Rule.

6.4.119

The area between and is 0.9544. By the Empirical Rule, the area between and is about 0.95.

Question 6.334

120. Checking the Empirical Rule. Check the accuracy of the Empirical Rule for . That is, find the area between and using the techniques of this section. Then compare your finding with the results for using the Empirical Rule.

Question 6.335

121. Without Tables or Technology. Find the following areas without using the table or technology. The area to the left of is 0.0668.

  1. Find the area to the right of .
  2. Find the area to the right of .
  3. Find the area between and .

6.4.121

(a) 0.0668 (b) 0.9332 (c) 0.8664

Question 6.336

122. Without Tables or Technology. Find the following areas without using the table or technology. The area to the right of is 0.0035.

  1. Find the area to the left of .
  2. Find the area to the left of .
  3. Find the area between and .

Question 6.337

123. Values of That Mark the Middle 99%. Find the two values of that contain the middle 99% of the area under the standard normal curve.

6.4.123

and .

Question 6.338

124. Values of That Mark the Middle 90%. Find the two values of that contain the middle 90% of the area under the standard normal curve.

Use the Normal Density Curve applet for Exercise 125.

Question 6.339

125. Find the quartiles of the standard normal distribution. That is, find the 25th, 50th, and 75th percentiles of the standard normal distribution.

6.4.125

−0.67; 0; 0.67

BRINGING IT ALL TOGETHER

image Chapter 6 Case Study: SAT Scores and AP Exam Scores

The College Board reports that the population mean Critical Reading SAT score in 2013 was = 496, with a population standard deviation of , and that the scores followed a normal distribution. Use this information for Exercises 126–131.

Question 6.340

126. Draw the graph of this distribution. Mark the number line with the increments of and .

Question 6.341

127. Suppose a different exam had the following parameter values: and . Explain how the distribution graph would be similar and how it would be different from the graph in Exercise 126.

6.4.127

The peak would still be at but since the standard deviation is larger the curve would be flatter and more spread out.

Question 6.342

128. Suppose a different exam had the following parameter values: and . Explain how the distribution graph would be similar and would be different from the graph in Exercise 126.

Question 6.343

129. What can we say about and ? What property of the normal distribution allows us to say this?

6.4.129

They are both equal to 0.5. The property that the mean equals the median.

Question 6.344

130. Which of the following probabilities is larger: or ? How do you know this?

Question 6.345

131. Confirm your work from Exercise 130 as follows: The -value associated with is , and the -value associated with is . Find and . Does this confirm your work from Exercise 130?

6.4.131

and ; yes