6.3 The Central Limit Theorem
In the early 1900s, W. S. Gossett discovered how the predictability of the normal curve could improve quality control in the Guinness ale factory. One of the practical problems that Gossett faced was related to sampling yeast cultures: too little yeast led to incomplete fermentation, whereas too much yeast led to a bitter-
MASTERING THE CONCEPT
6.4: The central limit theorem demonstrates that a distribution made up of the means of many samples (rather than individual scores) approximates a normal curve, even if the underlying population is not normally distributed.
The central limit theorem refers to how a distribution of sample means is a more normal distribution than a distribution of scores, even when the population distribution is not normal.
This small adjustment (taking the average of four samples rather than using just one sample) is possible because of the central limit theorem. The central limit theorem refers to how a distribution of sample means is a more normal distribution than a distribution of scores, even when the population distribution is not normal. Indeed, as sample size increases, a distribution of sample means more closely approximates a normal curve. More specifically, the central limit theorem demonstrates two important principles:
- Repeated sampling approximates a normal curve, even when the original population is not normally distributed.
- A distribution of means is less variable than a distribution of individual scores.

A distribution of means is a distribution composed of many means that are calculated from all possible samples of a given size, all taken from the same population.
Instead of randomly sampling a single data point, Gossett randomly sampled four data points from the population of 3000 and computed the average. He did this repeatedly and used those many averages to create a distribution of means. A distribution of means is a distribution composed of many means that are calculated from all possible samples of a given size, all taken from the same population. Put another way, the numbers that make up the distribution of means are not individual scores; they are means of samples of individual scores. Distributions of means are frequently used to understand data across a range of contexts; for example, when a university reports the mean standardized test score of incoming first-
144
Gossett experimented with using the average of four data points as his sample, but there is nothing magical about the number four. A mean test score for incoming students would have a far larger sample size. The important outcome is that a distribution of means more consistently produces a normal distribution (although with less variance) even when the population distribution is not normal. It might help your understanding to know that the central limit theorem works because a sample of four, for example, will minimize the effect of outliers. When an outlier is just one of four scores being sampled and averaged, the average won’t be as extreme as the outlier.
In this section, we learn how to create a distribution of means, as well as how to calculate a z score for a mean (more accurately called a z statistic when calculated for means rather than scores). We also learn why the central limit theorem indicates that, when conducting hypothesis testing, a distribution of means is more useful than a distribution of scores.
Creating a Distribution of Means
The central limit theorem underlies many statistical processes that are based on a distribution of means. A distribution of means is more tightly clustered (has a smaller standard deviation) than a distribution of scores.
EXAMPLE 6.10
In an exercise that we conduct in class with our students, we write the numbers in Table 6-1 on 140 individual index cards that can be mixed together in a hat. The numbers represent the heights, in inches, of 140 college students from the authors’ classes. As before, we treat these 140 students as the entire population.
- First, we randomly pull one card at a time and record its score by marking it on a histogram. After recording the score, we return the card to the container representing the population of scores and mix all the cards before pulling the next card. (Not surprisingly, this is known as sampling with replacement.) We continue until we have plotted at least 30 scores, drawing a square for each one so that bars emerge above each value. This creates the beginning of a distribution of scores. Using this method, we created the histogram in Figure 6-10.
- Now, we randomly pull three cards at a time, compute the mean of these three scores (rounding to the nearest whole number), and record this mean on a different histogram. As before, we draw a square for each mean, with each stack of squares resembling a bar. Again, we return each set of cards to the population and mix before pulling the next set of three. We continue until we have plotted at least 30 values. This is the beginning of a distribution of means. Using this method, we created the histogram in Figure 6-11.
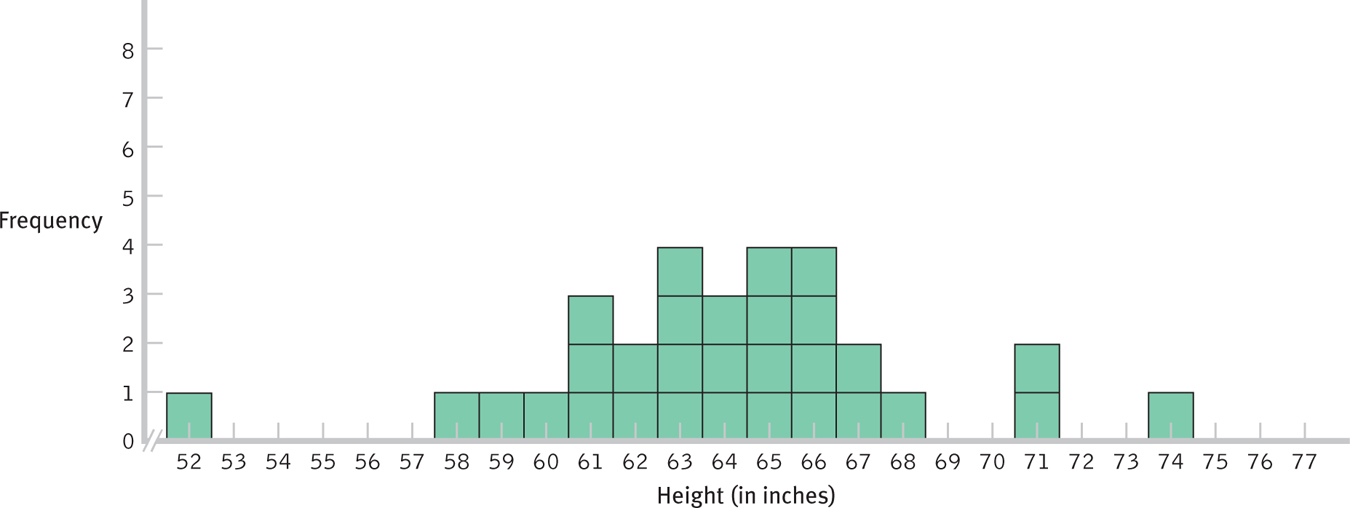
Figure 6-
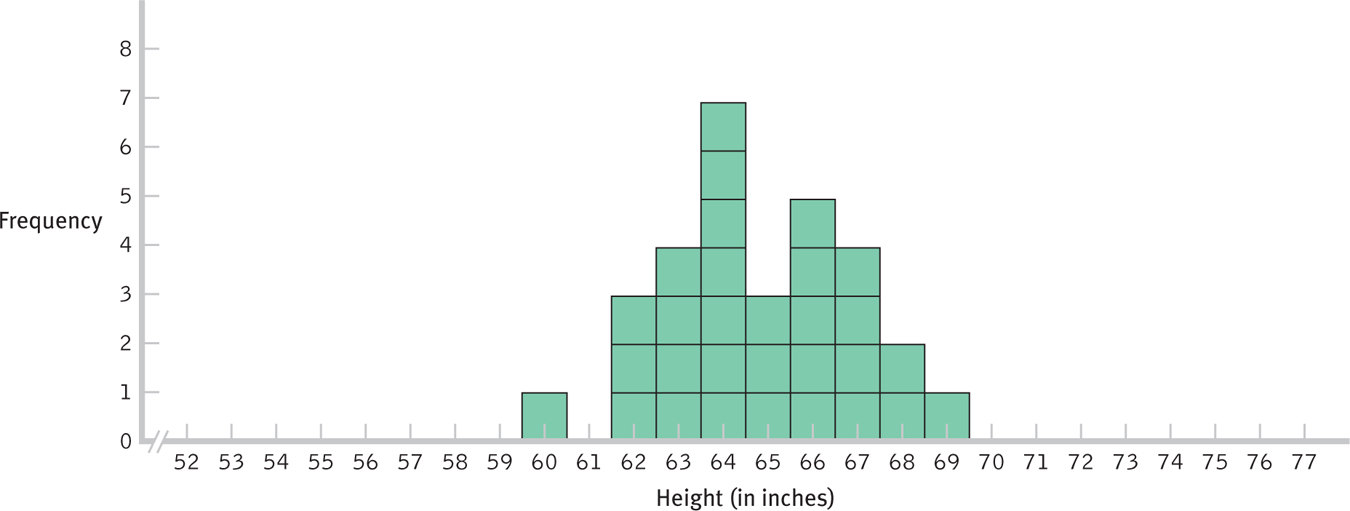
Figure 6-
145
The distribution of scores in Figure 6-10, similar to those we create when we do this exercise in class, ranges from 52 to 77 with a peak in the middle. If we had a larger population, and if we pulled many more numbers, the distribution would become more and more normal. Notice that the distribution is centered roughly around the actual population mean, 64.89. Also notice that all, or nearly all, scores fall within 3 standard deviations of the mean. The population standard deviation of these scores is 4.09. So nearly all scores should fall within this range:
64.89 − 3(4.09) = 52.62 and 64.89 + 3(4.09) = 77.16
In fact, the range of scores—
Is there anything different about the distribution of means in Figure 6-11? Yes, there are not as many means at the far tails of the distribution as in the distribution of scores—
Why does the spread decrease when we create a distribution of means rather than a distribution of scores? When we plotted individual scores, an extreme score was plotted on the distribution. But when we plotted means, we averaged that extreme score with two other scores. So each time we pulled a score in the 70s, we tended to pull two lower scores as well; when we pulled a score in the 50s, we tended to pull two higher scores as well.
What do you think would happen if we created a distribution of means of 10 scores rather than 3? As you might guess, the distribution would be even narrower because there would be more scores to balance the occasional extreme score. The mean of each set of 10 scores is likely to be even closer to the actual mean of 64.89. What if we created a distribution of means of 100 scores, or of 10,000 scores? The larger the sample size, the smaller the spread of the distribution of means.
146
Characteristics of the Distribution of Means
Because the distribution of means is less variable than the distribution of scores, the distribution of means needs its own standard deviation—
The data presented in Figure 6-12 allow us to visually verify that the distribution of means needs a smaller standard deviation. Using the population mean of 64.886 and standard deviation of 4.086, the z scores for the end scores of 60 and 69 are −1.20 and 1.01, respectively—
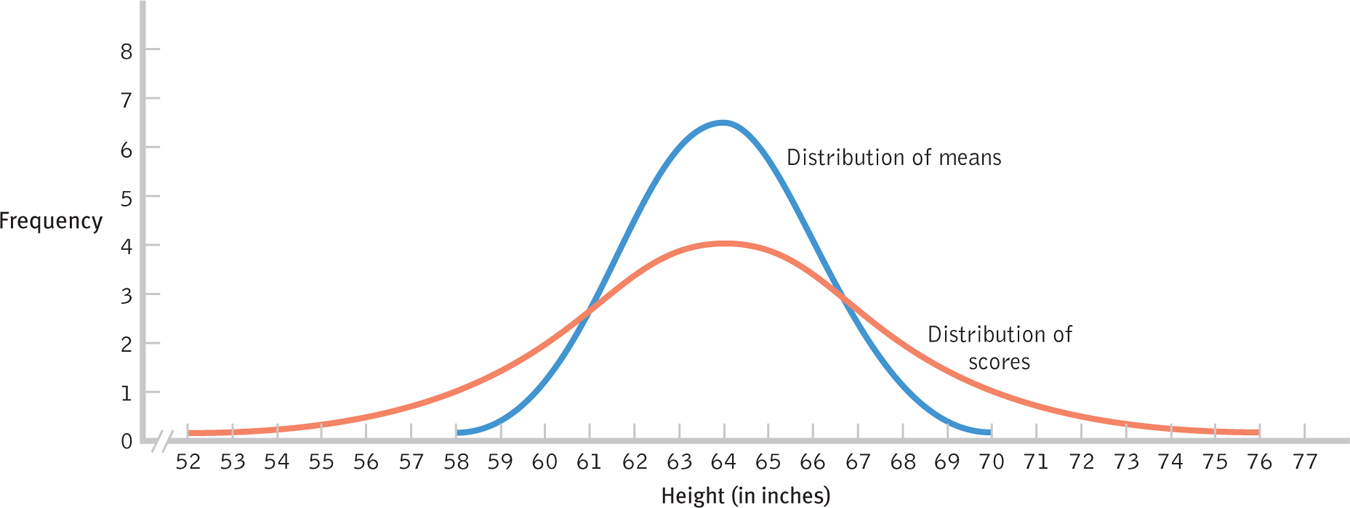
Figure 6-
MASTERING THE CONCEPT
6.5: A distribution of means has the same mean as a distribution of scores from the same population, but a smaller standard deviation.
Language Alert! We use slightly modified language and symbols when we describe distributions of means instead of distributions of scores. The mean of a distribution of means is the same as the mean of a population of scores, but it uses the symbol μM (pronounced “mew sub em”). The μ indicates that it is the mean of a population, and the subscript M indicates that the population is composed of sample means—the means of all possible samples of a given size from a particular population of individual scores.
Standard error is the name for the standard deviation of a distribution of means.
We also need a new symbol and a new name for the standard deviation of the distribution of means—
| Distribution | Symbol for Mean | Symbol for Spread | Name for Spread |
|---|---|---|---|
| Scores | μ | σ | Standard deviation |
| Means | μM | σM | Standard error |
Fortunately, there is a simple calculation that lets us know exactly how much smaller the standard error, σM, is than the standard deviation, σ. As we’ve noted, the larger the sample size, the narrower the distribution of means and the smaller the standard deviation of the distribution of means—
147
MASTERING THE FORMULA
6-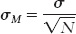 . We divide the standard deviation for the population by the square root of the sample size.
. We divide the standard deviation for the population by the square root of the sample size.
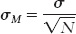
EXAMPLE 6.11
Imagine that the standard deviation of the distribution of individual scores is 5 and we have a sample of 10 people. The standard error would be:
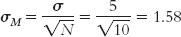
The spread is smaller when we calculate means for samples of 10 people because any extreme scores are balanced by less extreme scores. With a larger sample size of 200, the spread is even smaller because there are many more scores close to the mean to balance out any extreme scores. The standard error would then be:
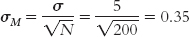
A distribution of means faithfully obeys the central limit theorem. Even if the population of individual scores is not normally distributed, the distribution of means will approximate the normal curve if the samples are composed of at least 30 scores. The three graphs in Figure 6-13 depict (a) a distribution of individual scores that is extremely skewed in the positive direction, (b) the less skewed distribution that results when we create a distribution of means using samples of 2, and (c) the approximately normal curve that results when we create a distribution of means using samples of 25. We have learned three important characteristics of the distribution of means:
148
- As sample size increases, the mean of a distribution of means remains the same.
- The standard deviation of a distribution of means (called the standard error) is smaller than the standard deviation of a distribution of scores. As sample size increases, the standard error becomes ever smaller.
- The shape of the distribution of means approximates the normal curve if the distribution of the population of individual scores has a normal shape or if the size of each sample that makes up the distribution is at least 30 (the central limit theorem).
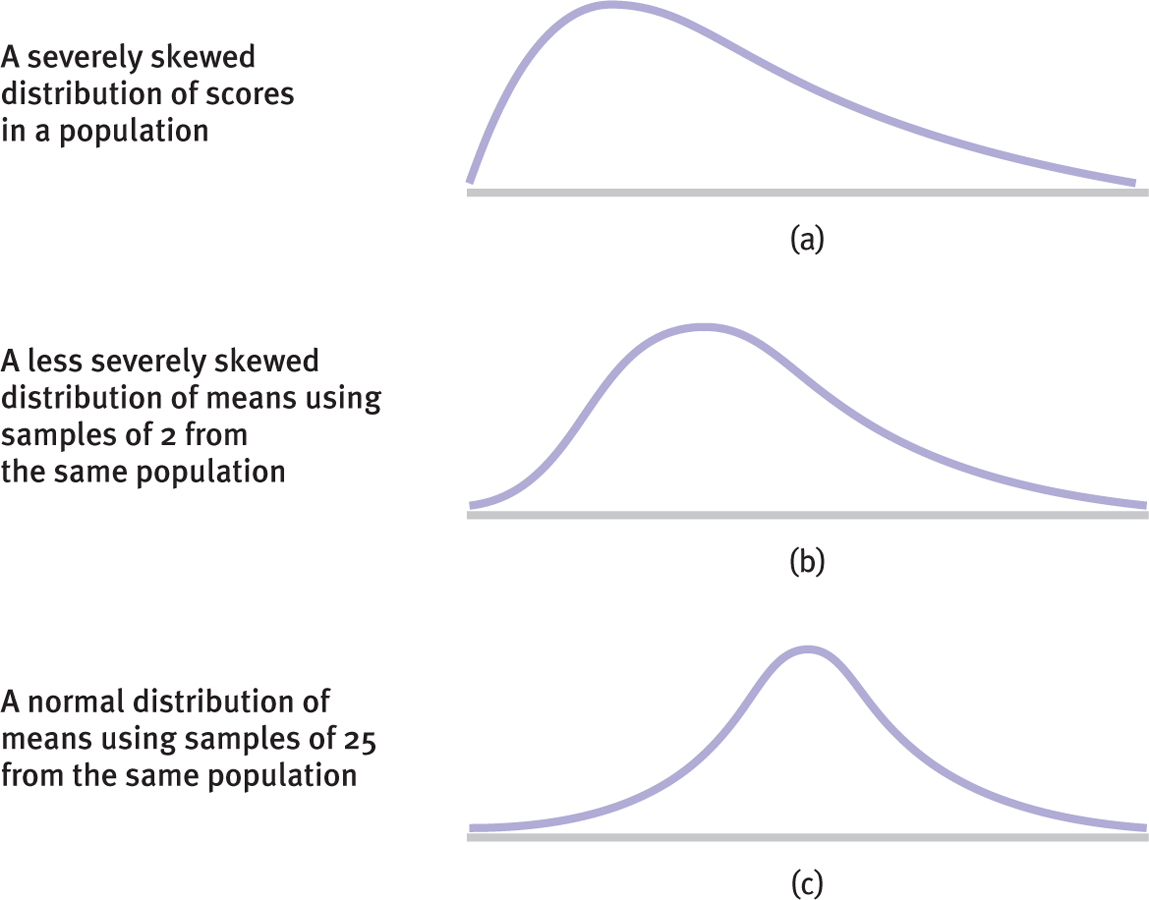
Figure 6-
Using the Central Limit Theorem to Make Comparisons with z Scores
z scores are a standardized version of raw scores based on the population. But we seldom have the entire population to work with, so we typically calculate the mean of a sample and calculate a z score based on a distribution of means. When we calculate the z score, we simply use a distribution of means instead of a distribution of scores. The z formula changes only in the symbols it uses:
MASTERING THE FORMULA
6-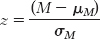 . We subtract the mean of the distribution of means from the mean of the sample, then we divide by the standard error, the standard deviation of the distribution of means.
. We subtract the mean of the distribution of means from the mean of the sample, then we divide by the standard error, the standard deviation of the distribution of means.
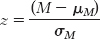
Note that we now use M instead of X because we are calculating a z score for a sample mean rather than for an individual score. Because the z score now represents a mean, not an actual score, it is often referred to as a z statistic. Specifically, the z statistic tells us how many standard errors a sample mean is from the population mean.
EXAMPLE 6.12
Let’s consider a distribution for which we know the population mean and standard deviation. Several hundred universities in the United States reported data from their counseling centers (Gallagher, 2009). (For this example, we’ll treat this sample as the entire population of interest.) The study found that an average of 8.5 students per institution were hospitalized for mental illness over 1 year. For the purposes of this example, we’ll assume a standard deviation of 3.8. Let’s say we develop a prevention program to reduce the numbers of hospitalizations and we recruit 30 universities to participate. After 1 year, we calculate a mean of 7.1 hospitalizations at these 30 institutions. Is this an extreme sample mean, given the population?
To find out, let’s imagine the distribution of means for samples of 30 hospitalization scores. We would collect the means the same way we collected the means of three heights in the earlier example—
149
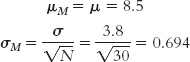
At this point, we have all the information we need to calculate the z statistic:
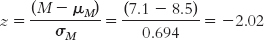
From this z statistic, we could determine how extreme the mean number of hospitalizations is in terms of a percentage. Then we could draw a conclusion about whether we would be likely to find a mean number of hospitalizations of 7.1 in a sample of 30 universities if the prevention program did not work. The useful combination of a distribution of means and a z statistic has led us to a point where we’re prepared for inferential statistics and hypothesis testing.
Next Steps
The Normal Curve and Catching Cheaters
Cheaters beware! Statisticians have applied principles based on the normal curve to identify patterns of extreme scores (see Lawrence Stedman’s 2011 report on cheating in the Atlanta school system, which led to numerous indictments of teachers and administrators). In their book Freakonomics, Steven Levitt and Stephen Dubner (2009) described alleged cheating among teachers in the Chicago public school system. Certain classrooms had suspiciously strong performances on standardized tests that often mysteriously declined the following year when a new teacher taught the same students. In about 5% of classrooms studied, Levitt and other researchers found blocks of correct answers among most students for the last few questions, an indication that the teacher had changed responses to difficult questions for most students. In one classroom, for example, 15 of 22 students gave identical answers to a string of six questions toward the end of a test, where the questions were more difficult. It did not take a large inferential leap to believe that these teachers were filling in the answers in order to artificially inflate their classes’ scores.
In another example, Alan Gerber and Neil Malhotra (2006) looked at all studies published between 1995 and 2004 in two political science journals, American Political Science Review and American Journal of Political Science, and recorded the z statistics reported in these studies. Gerber and Malhotra combined positive and negative z statistics, so any z statistic above 1.96 indicates that it was among the most extreme 5%. (As we noted in the Chapter 5 Next Steps, a cutoff of 5% is the norm in the social sciences; findings in the most extreme 5% are most likely to be published.) Then Gerber and Malhotra constructed a histogram (Figure 6-14) depicting the frequencies of the z statistics in these articles—
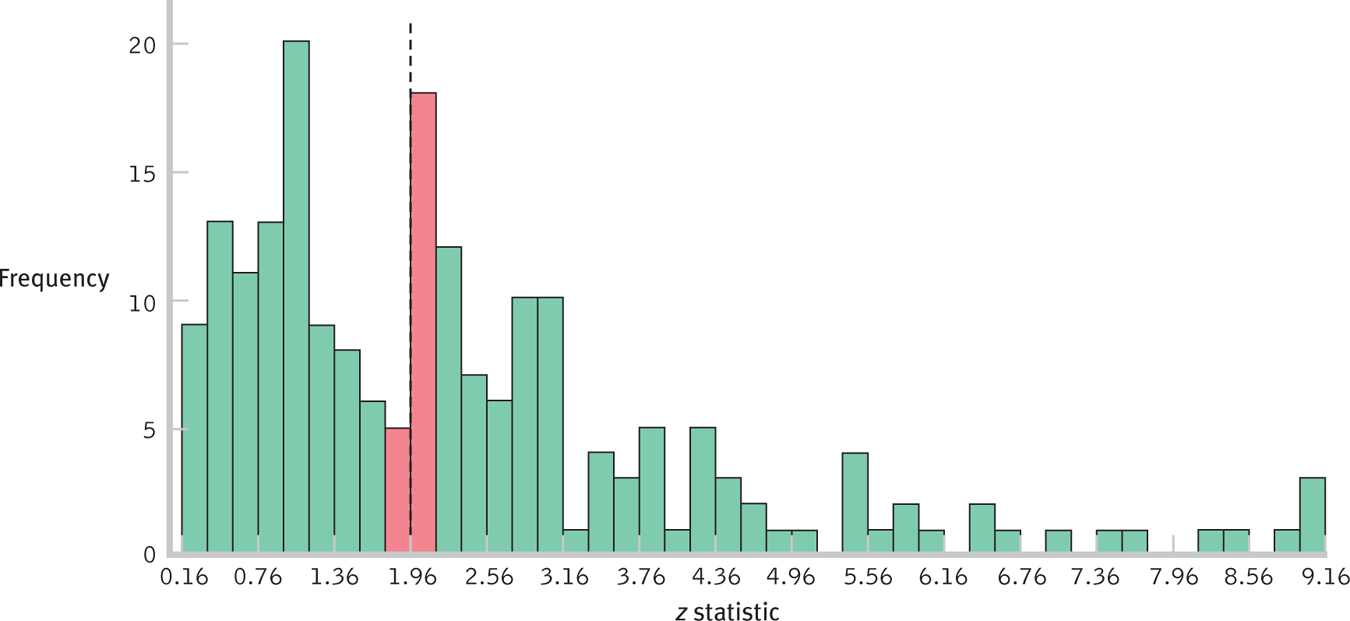
Figure 6-
What might be the source of this possible bias? There is nothing magical about the 0.05 (5%) cutoff; it is simply a reasonable standard that gives us a reasonable chance of detecting a real finding while minimizing the likelihood of committing a Type I error. The .05 level is the standard used by journal editors but guess what? The data don’t know about the 0.05 standard, so we would not expect any clustering of reported findings that, for example, just barely achieves that standard (anything less than 0.05). Let’s look at the data.
150
If we think of this histogram as one half of a normal curve, we notice a much lower frequency than would be expected for z statistics just below 1.96 (the 5% standard), as seen in the red bar just to the left of the dotted vertical line. And there was a much higher frequency than would be expected for z statistics just above 1.96, as seen in the red bar just to the right of the dotted vertical line. Gerber and Malhotra (2006) cite a “1 in 100 million” probability that the patterns they observed occurred just by chance (p. 3). What might account for this?
The authors suggest that the strict 5% cutoff is encouraging researchers to “play” with their data until it beats the cutoff. Some researchers may cheat in this way unwittingly, not realizing that they are biased. However, other researchers might cheat consciously, massaging the data with various analyses until it performs as they hope. The normal curve thus helped to identify a pattern of apparent cheating in social science publishing. Paying attention to the shape of distributions is not a sophisticated form of analysis. Yet such analysis could have flagged the enormous level of corruption at companies such as Enron, Global Crossing, and WorldCom—
CHECK YOUR LEARNING
Reviewing the Concepts
- According to the central limit theorem, a distribution of sample means based on 30 or more scores approximates the normal distribution, even if the original population is not normally distributed.
- A distribution of scores has the same mean as a distribution of means. However, a distribution of scores contains more extreme scores and a larger standard deviation than a distribution of means; this is another principle of the central limit theorem.
- z scores may be calculated from a distribution of scores or from a distribution of means. When we calculate a z score for a mean, we usually call it a z statistic.
- For the measure of spread, the two calculations use different terms: standard deviation for a distribution of scores and standard error for a distribution of means.
- Just as with z scores, the z statistic tells us about the relative position of a mean within a distribution; this can be expressed as a percentile.
- The normal curve can help identify observations caused by cheating that violate what we would expect by chance.
151
Clarifying the Concepts
- 6-
10 What are the main ideas behind the central limit theorem? - 6-
11 Explain what a distribution of means is.
Calculating the Statistics
- 6-
12 The mean of a distribution of scores is 57, with a standard deviation of 11. Calculate the standard error for a distribution of means based on samples of 35 people.
Applying the Concepts
- 6-
13 Let’s return to the selection of 30 CFC scores that we considered in Check Your Learning 6-2(b): 
- What is the range of these scores?
- Take three means of 10 scores each from this sample of scores, one for each row. What is the range of these means?
- Why is the range smaller for the means of samples of 10 scores than for the individual scores themselves?
- The mean of these 30 scores is 3.32. The standard deviation is 0.69. Using symbolic notation and formulas (where appropriate), determine the mean and standard error of the distribution of means computed from samples of 10.
Solutions to these Check Your Learning questions can be found in Appendix D.