15.4 An Application of Line Integrals: Work

OBJECTIVE

When you finish this section, you should be able to:

  1. Compute work (p. 1003)

An important application of a line integral is to work. Recall that work is the energy transferred to or from an object by a force acting on the object.

Let's review what we already know about work:

1003

Suppose \[\begin{equation*} \mathbf{F}=\mathbf{F}(x,y)=P(x,y)\mathbf{i}+Q(x,y)\mathbf{j} \end{equation*}\]

is a force field acting on an object at the point \((x,y)\) in some open, connected set \(R\). We assume the functions \(P\) and \(Q\) have continuous, first-order partial derivatives at each point in \(R\) and that \(C\) is a smooth curve lying entirely in \(R.\) Finally, suppose \(C\) is defined by the vector function \[\begin{equation*} \mathbf{r}=\mathbf{r}(t)=x(t)\mathbf{i}+y(t)\mathbf{j}\qquad a\leq t\leq b \end{equation*}\]

Partition the closed interval \([a,b]\) into \(n\) subintervals \[\begin{equation*} \lbrack a,t_{1}],\quad \lbrack t_{1},t_{2}],\quad \ldots ,\quad \lbrack t_{i-1},t_{i}],\quad \ldots ,\quad \lbrack t_{n-1},b] \end{equation*}\]

Figure 29

and denote the length of each subinterval by \(\Delta t_{1},\) \(\Delta t_{2},\) \(\ldots ,\) \(\Delta t_{n}\). Corresponding to each number \(a=t_{0},\) \(t_{1}, t_{2}, \ldots , t_{n}=b\) of the partition, there is a sequence of points \(A=p_{0},\) \(p_{1}, \ldots , p_{n}=B\) on the curve \(C\). These points subdivide the curve into \(n\) subarcs of lengths \(\Delta s_{1}, \ \Delta s_{2}, \ldots , \ \Delta s_{n}\), as shown in Figure 29.

The norm \(\Vert \Delta \Vert\) of the partition is the largest length of the subarcs \(\Delta s_{i},\) \(i=1, 2, \ldots , n\). Let \(p_{i}^{\ast}=(x_{i}^{\ast },y_{i}^{\ast })\) be a point on the \(i\)th subarc \(p_{i-1}p_{i}\) of \(C\). If the norm \(\Vert \Delta \Vert\) is small enough, then the work \(W_{i}\) done by the force field \(\mathbf{F}\) in moving an object along the arc \(p{_{i-1}p_{i}}\) can be approximated by the work done by the constant force \[\begin{equation*} \mathbf{F}_{i}^{\ast }=\mathbf{F}(x_{i}^{\ast },y_{i}^{\ast }) \end{equation*}\]

in moving the object along the directed line segment \(\Delta \mathbf{r}_{i}=\overrightarrow{p_{i-1}p_{i}}.\) Then \[\begin{equation*} W_{i}\approx \mathbf{F}_{i}^{\ast }\,{\cdot}\, \Delta \mathbf{r}_{i} \end{equation*}\]

The total work \(W\) done by \(\mathbf{F}\) along \(C\) from the point \(A\): \(\mathbf{r}=\mathbf{r}(a)\) to the point \(B\): \(\mathbf{r}=\mathbf{r}(b)\) is \(W=\lim\limits_{\left\Vert \Delta \right\Vert \rightarrow 0}\sum\limits_{i=1}^{n}W_{i}=\lim\limits_{\left\Vert \Delta \right\Vert \rightarrow 0}\sum\limits_{i=1}^{n}\mathbf{F}_{i}^{\ast }\,{\cdot}\, \Delta \mathbf{r}_{i}.\) This leads to the following definition:

spanDEFINITIONspan Work

Let \(\mathbf{F}=\mathbf{F}(x,y)=P(x,y)\mathbf{i}+Q(x,y)\mathbf{j}\) be a force field, where the functions \(P\) and \(Q\) are continuous with continuous partial derivatives at each point of an open, connected set \(R\). Let \(\mathbf{r}=\mathbf{r}(t)\), \(a\leq t\leq b\), trace out a piecewise-smooth curve \(C\) lying entirely in \(R\). The work \(W\) done by the force field \(\mathbf{F}\) in moving an object along \(C\) is defined as \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt] { W=\int_{C}\mathbf{F}\,{\cdot}\, d\mathbf{r}=\int_{C}(P\,dx+Q\,dy) }} \]

1 Compute Work

Computing Work

Find the work done by the force field \(\mathbf{F}(x,y)=-y\mathbf{i}+x\mathbf{j}\) in moving an object along the half-circle \(C\) traced out by \[ \mathbf{r}(t)=\cos t\,\mathbf{i}+\sin t\,\mathbf{j}\qquad 0\leq t\leq \pi \]

1004

Solution On \(C\), \(x(t)=\cos t\) and \(y(t)=\sin t,\) \(0\leq t\leq \pi\). Then \[ \begin{eqnarray*} \mathbf{F}( x(t),y(t)) & =&-y(t) \mathbf{i}+x(t) \mathbf{j}=-\sin t\,\mathbf{i}+\cos t\,\mathbf{j}\hbox{}\\ d\mathbf{r}(t)& =&( -\sin t\,\mathbf{i}+\cos t\,\mathbf{j}) \,dt \\[4pt] \mathbf{F}\,{\cdot}\, d\mathbf{r}& =&(\sin ^{2}t+\cos ^{2}t)\,dt=dt \end{eqnarray*} \]

The work \(W\) done by \(\mathbf{F}\) is \[ W=\int_{C}\mathbf{F}\,{\cdot}\, d\mathbf{r}=\int_{0}^{\pi }dt=\pi \]

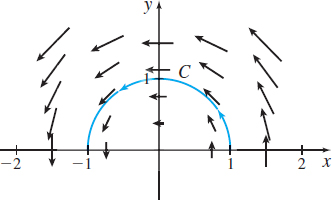
Figure 30 \(\mathbf{F}(x,y) = -y\mathbf{i} + x\mathbf{j}\)

See Figure 30 for the force field \(\mathbf{F}(x,y)=-y\mathbf{i}+x\mathbf{j}\) and the curve \(C\).

NOW WORK

Problem 13.

Work and Kinetic Energy

The work \(W\) done by a force field \(\mathbf{F}\) in moving an object along a piecewise-smooth curve \(C\) traced out by \(\mathbf{r}=\mathbf{r}(t)\), \(a\leq t\leq b\), is \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt] { W=\int_{C}\mathbf{F}\,{\cdot}\, d\mathbf{r}=\int_{a}^{b}\mathbf{F} \,{\cdot}\, \mathbf{r}' (t)\,dt }} \]

Using Newton's Second Law of Motion, \(\mathbf{F}=m\mathbf{r}'' (t)\), where \(\mathbf{r}'' (t)\) is the acceleration of the object, we find that work \(W\) can be expressed as \[ \begin{eqnarray*} W=\int_{a}^{b}\mathbf{F}\,{\cdot}\, \mathbf{r}' (t)\,dt&\underset{\underset{\color{#0066A7}{\mathbf{F}=m\mathbf{r}'' (t)}}{\color{#0066A7}{\uparrow }}}{=}&\int_{a}^{b}m \mathbf{r}'' (t)\,{\cdot}\, \mathbf{r}' (t)\,dt\underset{\underset{\color{#0066A7} {\dfrac{d}{dt}[\mathbf{r}' (t)\,{\cdot}\, \mathbf{r}' (t)]=2 [\mathbf{r}'' (t)\,{\cdot}\, \mathbf{r}' (t) ]}}{\color{#0066A7}{\uparrow }}}{=}\dfrac{m}{2}\int_{a}^{b}\dfrac{d}{dt}[ \mathbf{r}^{\prime }(t)\,{\cdot}\, \mathbf{r}^{\prime }(t)]\,dt \nonumber\\ &\underset{\underset{\color{#0066A7}{\mathbf{r}^{\prime }\!\cdot\!\mathbf{r}^{\prime } = \left\Vert \mathbf{r}^{\prime }\right\Vert ^{2}}}{\color{#0066A7}{\uparrow }}}{=}&\dfrac{m}{2}\int_{a}^{b}\dfrac{d}{dt}\left\Vert \mathbf{r}' (t) \right\Vert ^{2}dt=\left. \dfrac{m}{2}\left\Vert \mathbf{r' (t)}\right\Vert ^{2}\right] _{a}^{b}\tag{1} \end{eqnarray*} \]

Kinetic energy \(K\) is the energy of motion. The kinetic energy \(K\) of an object of mass \(m\) that moves along a curve with speed \(\left\Vert \mathbf{v} \right\Vert\) is given by \[ \begin{eqnarray*}\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt] {{ K=\dfrac{1}{2}m\Vert \mathbf{v}\Vert ^{2}\underset{\underset{\color{#0066A7}{\hbox{\(\mathbf{v}=\mathbf{r}' (t)\)}}}{\color{#0066A7}{\uparrow}}}{=}\dfrac{m}{2}\left\Vert \mathbf{r' (t)}\right\Vert ^{2} \\[-6.3pt] }}} \tag{2} \end{eqnarray*} \]

By combining (1) and (2), we obtain \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt] { W=K(b)-K(a) }} \]

which relates work \(W\) to kinetic energy \(K\). In other words, \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt] { \left[ \begin{eqnarray*} \hbox{Work \(W\) done by a force field \(\mathbf{F}\)} \\ \hbox{in moving an object from \(a\) to \(b\)} \end{eqnarray*}\right] = [ \hbox{Change in the kinetic energy \(K\) from \(a\) to \(b\)}] }} \]

If the curve \(C\) is closed and the force field \(\mathbf{F}\) is conservative, then it follows that \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt] { \hbox{Work} =\int_{C}\mathbf{F}\,{\cdot}\, d\mathbf{r}=0 }} \]

THEOREM Work on a Closed Path

In a conservative force field \(\mathbf{F}\), the work \(W\) done by \(\mathbf{F}\) in moving an object along a closed path is \(0\). That is, the object returns to its original position with the same kinetic energy it started with.

1005

The work done by a conservative force field \(\mathbf{F}\) is independent of the path. Physicists paraphrase this by saying that, in a conservative force field, work is a function of position and not path.

Gravitational force is an example of a conservative force field. But not all forces \(\mathbf{F}\) are conservative, as we show in Example 2.

Showing a Force Field Is Not a Conservative Vector Field

  1. Show that the force field \(\mathbf{F}=( x+y) \mathbf{i} +( y-x) \mathbf{j}\) is not a conservative vector field.
  2. Show that the work \(W\) done by \(\mathbf{F}\) in moving an object is dependent on the path by using two paths starting at the origin \((0,0)\) and ending at the point \((1,1)\).

Solution (a) Let \(P(x,y) =x+y\) and \(Q(x,y) =y-x.\) Then \[ \dfrac{\partial P}{\partial y}=\dfrac{\partial }{\partial y}(x+y) =1\qquad\hbox{and}\qquad \dfrac{\partial Q}{\partial x}=\dfrac{\partial }{\partial x}(y-x) =-1 \]

Since \(\dfrac{\partial P}{\partial y}\neq \dfrac{\partial Q}{\partial x}\), the force field \(\mathbf{F}\) is not a conservative vector field.

(b) To show that the work \(W\) done by \(\mathbf{F}\) is dependent on the path, we choose two paths beginning at the origin \((0,0)\) and ending at the point \((1,1)\).

For Path 1, we let \(C\) be defined by \(y=x\), where \(0\leq x\leq 1.\) That is, \(x(t) =t,\) \(y(t) =t,\) \(0\leq t\leq 1.\) Then \(\mathbf{F}( x(t),y(t)) =2t\,\mathbf{i}\), \(\mathbf{r}(t) =t\mathbf{i}+t\mathbf{j}\), and \(d\mathbf{r=\,}\left( \mathbf{i}+\mathbf{j}\right) dt.\) So, \[\begin{equation*} \mathbf{F}\,{\cdot}\, d\mathbf{r}=2t\,dt \end{equation*}\]

The work \(W\) done by \(\mathbf{F}\) along \(C\) is \[ W=\int_{C}\mathbf{F}\,{\cdot}\, d\mathbf{r}=\int_{0}^{1}2t\,dt=\big[ t^{2}\big] _{0}^{1}=1 \]

For Path 2, we let \(C\) be the piecewise-smooth curve made up of:

  • \(C_{1},\) which is traced out by \(x(t) =t,\) \(y(t) =0,\) \(0\leq t\leq 1,\) and
  • \(C_{2},\) which is traced out by \(x(t) =1,\) \(y(t) =t,\) \(0\leq t\leq 1\).

For \(C_{1},\) \(\mathbf{F}( x(t),y(t)) =t\,\mathbf{i}-t\mathbf{j}\), \(\mathbf{r}(t) =t\mathbf{i}\), and \(d\mathbf{r}=\mathbf{i}\,dt\). So, \[ \mathbf{F}\,{\cdot}\, d\mathbf{r}=t\,dt \]

For \(C_{2},\) \(\mathbf{F}( x(t),y(t)) =( 1+t) \,\mathbf{i}+( t-1) \mathbf{j}\), \(\mathbf{r}(t) =\mathbf{i}+t \mathbf{j}\), and \(d\mathbf{r}=\mathbf{j}\,dt\). So, \[\begin{equation*} \mathbf{F}\,{\cdot}\, d\mathbf{r}=( t-1)\, dt \end{equation*}\]

The work \(W\) done by \(\mathbf{F}\) along Path 2 is \[\begin{equation*} W=\int_{C_{1}}\mathbf{F}\,{\cdot}\, d\mathbf{r}\,+\int_{C_{2}}\mathbf{F}\,{\cdot}\, d \mathbf{r}=\int_{0}^{1}t\,dt +\int_{0}^{1}( t-1)\, dt=0 \end{equation*}\]

Since the work done along Path 1 and Path 2 are not equal, the work \(W\) done by the force \(\mathbf{F}\) is dependent on the path.

NOW WORK

Problem 21.

NOTE

Potential energy \(U\) is the energy of position in a system.

Work and Potential Energy

Suppose an object of mass \(m\) moves along a smooth curve \(C\) traced out by \(\mathbf{r}=\mathbf{r}(t)\), \(a\leq t\leq b,\) in a conservative force field \(\mathbf{F}=\mathbf{F}(x,y)\). The potential energy \(U=U(x,y)\) of the object due to \(\mathbf{F}\) is the function \(U\) for which \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt] { \nabla U=-\mathbf{F} }} \]

1006

That is, \(U\) is the negative of the potential function for \(\mathbf{F}\). The work \(W\) done by \(\mathbf{F}\) in moving an object along \(C\) from \(a\) to \(b\) is \[ \begin{eqnarray*} W=\int_{C}\mathbf{F}\,{\cdot}\, d\mathbf{r}=-\int_{C}{\nabla }U\,{\cdot}\, d\mathbf{r}=- \big[U(x,y)\big] _{a}^{b}=- [U ( \mathbf{r} ( b) ) -U ( \mathbf{r} ( a) ) ] =U ( \mathbf{r} ( a) ) -U ( \mathbf{r}(b)) \end{eqnarray*} \]

This equation relates work \(W\) to potential energy \(U,\) as stated below. \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt] { \left[ \begin{eqnarray*} \hbox{The work \(W\) done by a force field \(\mathbf{F}\)} \\ \hbox{in moving an object from \(a\) to \(b\)} \end{eqnarray*}\right] =[\hbox{The change in potential energy \(U\) from \(b\) to \(a\)}] }} \]

Now we can state and prove the Law of Conservation of Energy.

Law of Conservation of Energy

In a conservative force field \(\mathbf{F}\), the sum of the potential and kinetic energies of an object is constant.

Proof

The potential energy \(U=U(x,y)\) of an object moving along a curve \(C\) in a conservative field of force \(\mathbf{F}\) obeys \[\begin{equation*} {\nabla }U=-\mathbf{F}(x,y) \end{equation*}\]

If an object of mass \(m\) moves along the curve \(C\) traced out by \(\mathbf{r}=\mathbf{r}(t)\), \(a\leq t\leq b,\) its kinetic energy \(K\) is \[\begin{equation*} K=\dfrac{1}{2}m\left\Vert \mathbf{r}' (t) \right\Vert ^{2}= \dfrac{1}{2}m[\mathbf{r}' (t)\,{\cdot}\, \mathbf{r}' (t)] \end{equation*}\]

Let \(E=E(t)\) equal the sum of the potential and kinetic energies of the object at time \(t\). Then \[\begin{equation*} E(t)=U+K=U(x,y)+\dfrac{m}{2}[\mathbf{r}' (t)\,{\cdot}\, \mathbf{r}' (t)] \end{equation*}\]

We show that \(E\) is constant by showing that \(E' (t)=0\): \[\begin{eqnarray*} E' (t)\underset{\underset{\color{#0066A7}{\hbox{Use Chain Rule I with \(U\)}}}{\color{#0066A7}{\uparrow}}}{=} \dfrac{\partial U}{\partial x}\dfrac{dx}{dt}+\dfrac{\partial U}{\partial y} \dfrac{dy}{dt}+m[\mathbf{r}' (t)\,{\cdot}\, \mathbf{r}'' (t)]\\[-9.5pt] \end{eqnarray*}\]

But \[\begin{eqnarray*} \mathbf{r}' (t)=\dfrac{dx}{dt}\,\mathbf{i}+\dfrac{dy}{dt}\,\mathbf{j} \qquad \hbox{and}\qquad \dfrac{\partial U}{\partial x}\mathbf{i}+\dfrac{ \partial U}{\partial y}\mathbf{j}={\nabla }U=-\mathbf{F}\underset{\underset{\color{#0066A7}{\hbox{\(\mathbf{F}\,=\,m\mathbf{a}\)}}}{\color{#0066A7}{\uparrow}}}{=}-m\mathbf{r}'' (t) \end{eqnarray*}\]

So, \[ \dfrac{\partial U}{\partial x}\dfrac{dx}{dt}+\dfrac{\partial U}{\partial y} \dfrac{dy}{dt}={\nabla }U\,\cdot\, \mathbf{r}' (t) =-m\,\mathbf{r}'' (t) \,\cdot\, \mathbf{r}' (t) \]

Then \[\begin{equation*} E' (t)=-m[\mathbf{r}'' (t)\,{\cdot}\, \mathbf{r}' (t)]+m[ \mathbf{r}' (t)\,{\cdot}\, \mathbf{r}'' (t)]=0 \end{equation*}\]

That is, the energy \(E\) of the object is constant.