3.5 Taylor Polynomials
240
OBJECTIVES
When you finish this section, you should be able to:
- Find a Taylor Polynomial (p. 240)
In the last section, we found that if a function \(f\) is differentiable in an interval \(( a,b) \), then a linear approximation \(L( x)\) to \(f\) at a number \(x_{0}\) in the interval is given by \[ L( x) =f( x_{0}) +f^\prime ( x_{0}) ( x-x_{0}) \]
where \(y=L( x) \) is the tangent line to the graph of \(f\) at the point \(( x_{0}, f( x_{0}))\). This approximation for \(f\) is good if \(x\) is close enough to \(x_{0}\), but as the interval widens, the accuracy of the estimate decreases.
The linear approximation \(y=L( x) \) is a first degree polynomial function. If the function \(f\) has derivatives of orders \(1\) to \(n\) at \(x_{0}\), then a polynomial function \(P_{n}( x) \) of degree \(n\) can be used to approximate \(f\) near \(x_{0}\).
ORIGINS
The Taylor polynomial is named after the English mathematician Brook Taylor (1685–1731). Taylor grew up in an affluent but strict home. He was home-schooled in the arts and the classics until he attended Cambridge University in 1703, where he studied mathematics. He was an accomplished musician and painter as well as a mathematician.
To be sure that the polynomial approximation \(P_{n}( x) \) fits \(f\) well, we require: \[ P_{n}( x_{0}) =f( x_{0})\quad P_{n}^\prime ( x_{0}) =f^\prime ( x_{0})\quad P_{n}^{\prime \prime} ( x_{0}) =f^{\prime \prime} ( x_{0}) \ldots P_{n}^{(n)}( x_{0}) =f^{( n) }( x_{0}) \]
That is, the value at \(x_{0}\) of the function \(f\) and its first \(n\) derivatives equals the value at \(x_{0}\) of the polynomial approximation and its first \(n\) derivatives.
spanDEFINITIONspan Taylor Polynomial
If a function \(f\) and its first \(n\) derivatives are defined on an interval containing the number \(x_{0}\), then \[\bbox[5px, border:1px solid black, #F9F7ED]{P_{n}( x) =f( x_{0}) +f^\prime ( x_{0}) ( x-x_{0}) +\dfrac{f^{\prime \prime} ( x_{0}) }{2!}( x-x_{0}) ^{2}+\cdots+\dfrac{f^{( n) }( x_{0}) }{\,n!}( x-x_{0}) ^{n}} \] is called the \(n\)th Taylor Polynomial for \(f\) at \(x_{0}\).
NOTE
The sum of the first two terms of a Taylor Polynomial is the linear approximation of \(f\) at \(x\). That is, \({P}_{1}({x}) = L({x})\).
1 Find a Taylor Polynomial
Finding a Taylor Polynomial for \(f( x)=\sqrt{x}\)
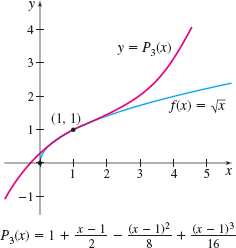
Find the Taylor Polynomial \(P_{3}( x) \) for \(f( x) =\sqrt{x}\) at \(1.\)
Solution The first three derivatives of \(f(x) =\sqrt{x}\) are \[ \begin{eqnarray*} f^\prime ( x) &=&\dfrac{1}{2\sqrt{x}}\qquad\qquad f^{\prime \prime} ( x) =\dfrac{d}{dx}\left( \dfrac{x^{-1/2}}{2}\right) =-\dfrac{1}{4x^{3/2}} \\ f^{\prime \prime \prime} ( x) &=&\dfrac{d}{dx}\left( -\dfrac{x^{-3/2}}{4}\right) =\dfrac{3}{8x^{5/2}} \end{eqnarray*} \]
Then \[ f(1) =1\qquad f^\prime (1) =\dfrac{1}{2}\qquad f^{\prime \prime} (1) =-\dfrac{1}{4}\qquad f^{\prime \prime \prime} (1) =\dfrac{3}{8} \]
The Taylor Polynomial \(P_{3}( x) \) for \(f( x) =\sqrt{x} \) at \(1\) is \[ \begin{eqnarray*} P_{3}( x) &=&f(1) +f^\prime (1) ( x-1) +\dfrac{f^{\prime \prime} (1) }{2!}( x-1) ^{2}+\dfrac{f^{\prime \prime \prime} (1) }{3!}( x-1)^{3}\\ &=&1+\dfrac{x-1}{2}-\dfrac{( x-1) ^{2}}{8}+\dfrac{( x-1) ^{3}}{16} \end{eqnarray*} \]
The graphs of the function \(f\) and the Taylor Polynomial \(P_{3}\) are shown in Figure 17. Notice how \(P_{3}( x) \approx f( x)\) for values of \(x\) near \(1\).
NOW WORK
Problem 11.
241
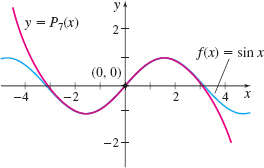
Finding a Taylor Polynomial for \(f( x) =\sin x\)
Find the Taylor Polynomial \(P_{7}( x) \) for \(f( x) =\sin x\) at \(0\).
Solution The derivatives of \(f( x) =\sin x\) at \(0\) are \[ \begin{array}{rcl@{\qquad}rcl@{\qquad}rcl@{\qquad}rcl} f( x) &=&\sin x & f^\prime ( x) &=&\cos x & f^{\prime \prime} ( x) &=&-\!\sin x & f^{\prime \prime \prime} ( x) &=&-\!\cos x \\ f( 0) &=&0 & f^\prime ( 0) &=&1 & f^{\prime \prime} ( 0) &=&0 & f^{\prime \prime \prime} ( 0) &=&-1 \\ f^{( 4) }( x) &=&\sin x & f^{(5) }( x) &=&\cos x & f^{( 6)}( x) &=&-\!\sin x & f^{( 7) }( x) &=&-\!\cos x \\ f^{( 4) }( 0) &=&0 & f^{(5) }( 0) &=&1 & f^{( 6) }( 0) &=&0 & f^{( 7) }( 0) &=&-1 \end{array} \]
The Taylor Polynomial \(P_{7}( x) \) for \(\sin x\) at \(0\) is \[ P_{7}( x) =f( 0) +f^\prime ( 0) x+\dfrac{f^{\prime \prime} ( 0) }{2!}x^{2}+\dfrac{f^{\prime\prime \prime} ( 0) }{3!}x^{3}+\cdots +\dfrac{f^{( 7) }( 0) }{7!}x^{7}=x-\dfrac{x^{3}}{3!}+\dfrac{x^{5}}{5!}-\dfrac{x^{7}}{7!} \]
Figure 18 shows the graph of \(P_{7}\) superimposed on the graph of \(y=\sin x\).
NOW WORK
Problem 13.
Finding a Taylor Polynomial for \(f( x) =e^{x}\)
Find the Taylor Polynomial \(P_{n}( x) \) for \(f( x) =e^{x}\) at \(0\).
Solution The derivatives of \(f( x) =e^{x}\) are \[ \begin{array}{rcl@{\qquad}rcl@{\qquad}rcl@{\qquad}rcl@{ }c@{ }rcl} f( x) = e^{x} & f^\prime ( x) = e^{x} & f^{\prime \prime} ( x) = e^{x} & f^{\prime \prime \prime} ( x) = e^{x} & \ldots & f^{( n) }( x) = e^{x} \\ f( 0) = 1 & f^\prime ( 0) = 1 & f^{\prime \prime} ( 0) = 1 & f^{\prime \prime \prime} ( 0) = 1 & \ldots & f^{( n)}( 0) = 1 \end{array} \]
The Taylor Polynomial \(P_{n}( x) \) at \(0\) is \[ \begin{eqnarray*} P_{n}( x) &=&f( 0) +f^\prime ( 0) x+\dfrac{ f^{\prime \prime} ( 0) }{2!}x^{2}+\dfrac{f^{\prime \prime\prime} ( 0) }{3!}x^{3}+\cdots +\dfrac{f^{( n) }( 0) }{n!}x^{n}\\ &=&1+x+\dfrac{x^{2}}{2!}+\dfrac{x^{3}}{3!}+\cdots +\dfrac{ x^{n}}{n!} \end{eqnarray*} \]
NOTE
In Chapter 8 we investigate the relationship between a function \(f\) and its Taylor Polynomials.
Figure 19 illustrates how the graphs of the Taylor Polynomials \(P_{1}( x) ,\) \(P_{2}( x) ,\) and \(P_{3}( x) \) compare to the graph of \(f( x) =e^{x}\) near \(0.\)
