17-2 If a star’s distance is known, its luminosity can be determined from its apparent brightness
 All the stars you can see in the nighttime sky shine by thermonuclear fusion, just as the Sun does (see Section 16-1). But they are by no means merely identical copies of the Sun. Stars differ in their luminosity (L), the amount of light energy they emit each second. Luminosity is usually measured either in watts (1 watt, or 1 W, is 1 joule per second) or as a multiple of the Sun’s luminosity (L⊙, equal to 3.90 × 1026 W). Most stars are less luminous than the Sun, but some blaze forth with a million times the Sun’s luminosity. Knowing a star’s luminosity is essential for determining the star’s history, its present-day internal structure, and its future evolution.
All the stars you can see in the nighttime sky shine by thermonuclear fusion, just as the Sun does (see Section 16-1). But they are by no means merely identical copies of the Sun. Stars differ in their luminosity (L), the amount of light energy they emit each second. Luminosity is usually measured either in watts (1 watt, or 1 W, is 1 joule per second) or as a multiple of the Sun’s luminosity (L⊙, equal to 3.90 × 1026 W). Most stars are less luminous than the Sun, but some blaze forth with a million times the Sun’s luminosity. Knowing a star’s luminosity is essential for determining the star’s history, its present-day internal structure, and its future evolution.
Luminosity, Apparent Brightness, and the Inverse-Square Law
Imagine a star radiating light into space. As the light energy moves away from the star, it spreads out over increasingly larger regions of space—the energy thins out. Now imagine a sphere of radius d centered on the star, as in Figure 17-4. The amount of energy that passes each second through a square meter of the sphere’s surface area is called the brightness (b). The brightness is the total luminosity of the source (L) divided by the total surface area of the sphere (equal to 4πd2). This quantity is also called the apparent brightness (b), because how bright a light source appears depends on how far away it is being observed. Apparent brightness is measured in watts per square meter (W/m2).
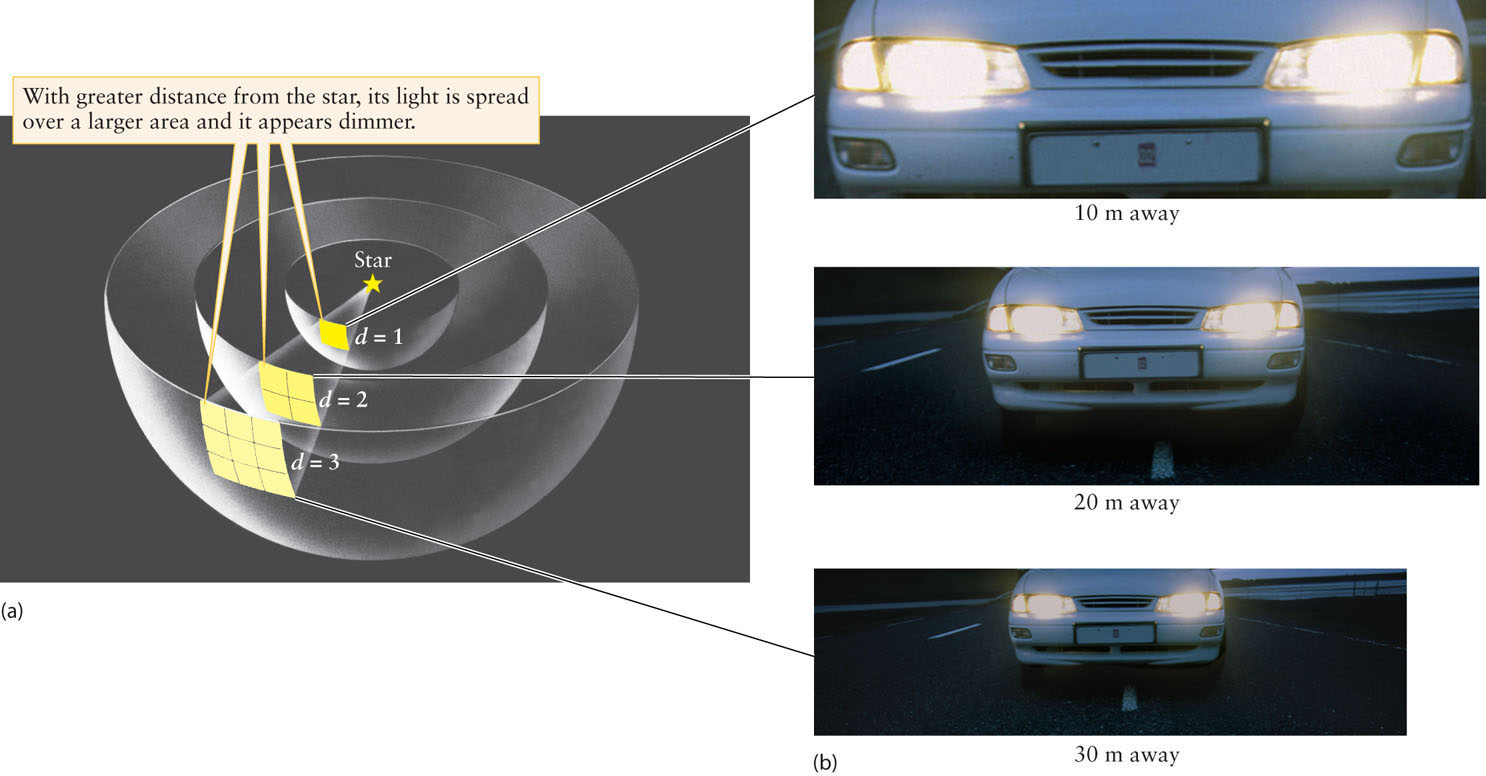
 The Inverse-Square Law Radiation from a light source illuminates an area that increases as the square of the distance from the source. Hence, the apparent brightness decreases as the square of the distance. The brightness at d = 2 is 1/(22) = ¼ of the brightness at d = 1, and the brightness at d = 3 is 1/(32) = 1/9 of that at d = 1.
The Inverse-Square Law Radiation from a light source illuminates an area that increases as the square of the distance from the source. Hence, the apparent brightness decreases as the square of the distance. The brightness at d = 2 is 1/(22) = ¼ of the brightness at d = 1, and the brightness at d = 3 is 1/(32) = 1/9 of that at d = 1.
Apparent brightness is a measure of how faint a star looks to us; luminosity is a measure of the star’s total light output
Written in the form of an equation, the relationship between apparent brightness and luminosity is
Inverse-square law relating apparent brightness and luminosity
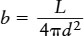
- b = apparent brightness of a star’s light, in W/m2
- L = star’s luminosity, in watts
- d = distance to star, in meters
This relationship is called the inverse-square law, because the apparent brightness of light that an observer can see or measure is inversely proportional to the square of the observer’s distance (d) from the source. If you double your distance from a light source, its radiation is spread out over an area 4 times larger, so the apparent brightness you see is decreased by a factor of 4. Similarly, at triple the distance, the apparent brightness is 1/9 as great (see Figure 17-4).
We can apply the inverse-square law to the Sun, which is 1.50 × 1011 m from Earth. Its apparent brightness (b⊙) is
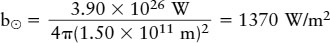
That is, a solar panel with an area of 1 square meter receives 1370 watts of power from the Sun.
When astronomers measure the apparent brightness of a star, the process is called photometry.
CAUTION!
No matter what your distance is from a star, the star’s luminosity (L) remains unchanged. Luminosity is the intrinsic energy output of the star. Only the apparent brightness (b) changes with distance as the star’s energy thins out. Furthermore, a big telescope and a small telescope on Earth will both measure the same apparent brightness; while a larger telescope collects more light, its larger lens or mirror is taken into account when computing b.
CALCULATION CHECK 17-2
How many times less light falls on a book illuminated by a lightbulb if the book is moved a distance of 3 times farther away?
According to the inverse-square law nature of light, the intensity of the light received decreases with the square of the distance. In this instance, increasing the distance 3 times means the newspaper receives only 1/(3)2 or one-ninth the amount of light it originally received.
Calculating a Star’s Luminosity
The inverse-square law says that we can find a star’s luminosity if we know its distance and its apparent brightness. For convenience, this law can be expressed in a somewhat different form. We first rearrange the above equation:
L = 4πd2b
We then apply this equation to the Sun. That is, we write a similar equation relating the Sun’s luminosity (L⊙), the distance from Earth to the Sun (d⊙, equal to 1 AU), and the Sun’s apparent brightness (b⊙):
L⊙ = 4πd⊙2b⊙
If we take the ratio of these two equations, the unpleasant factor of 4π drops out and we are left with the following:
Determining a star’s luminosity from its apparent brightness
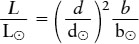

We need to know just two things to find a star’s luminosity: the distance to a star as compared to the Earth-Sun distance (the ratio d/d⊙), and how that star’s apparent brightness compares to that of the Sun (the ratio b/b⊙). Then we can use the above equation to determine how luminous that star is compared to the Sun (the ratio L/L⊙).
In other words, this equation gives us a general rule relating the luminosity, distance, and apparent brightness of a star:
We can determine the luminosity of a star from its distance and apparent brightness. For a given distance, the brighter the star, the more luminous that star must be. For a given apparent brightness, the more distant the star, the more luminous it must be to be seen at that distance.
Box 17-2 shows how to use the above equation to determine the luminosity of the nearby star ε (epsilon) Eridani, the fifth brightest star in the constellation Eridanus (named for a river in Greek mythology). Parallax measurements indicate that ε Eridani is 3.23 pc away, and photometry shows that the star appears only 6.73 × 10−13 as bright as the Sun. Using the above equation, we find that ε Eridani has only 0.30 times the luminosity of the Sun.
BOX 17-2 TOOLS OF THE ASTRONOMER’S TRADE
Luminosity, Distance, and Apparent Brightness
The Inverse-square law (Section 17-2) relates a star’s luminosity, distance, and apparent brightness to the corresponding quantities for the sun:
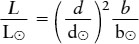
We can use a similar equation to relate the luminosities, distances, and apparent brightnesses of any two stars, which we call star 1 and star 2:
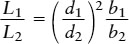
EXAMPLE: The star ε (epsilon) Eridani is 3.23 pc from Earth. As seen from Earth, this star appears only 6.73 × 10−13 as bright as the Sun. What is the luminosity of ε Eridani compared with that of the Sun?
Situation: We are given the distance to ε Eridani (d = 3.23 pc) and this star’s brightness compared to that of the Sun (b/b⊙ = 6.73 × 10−13). Our goal is to find the ratio of the luminosity of ε Eridani to that of the Sun, that is, the quantity L/L⊙.
Tools: Since we are asked to compare this star to the Sun, we use the first of the two equations given above, L/L⊙ = (d/d⊙)2(b/b⊙), to solve for L/L⊙.
Answer: Our equation requires the ratio of the star’s distance to the Sun’s distance, d/d⊙. The distance from Earth to the Sun is d⊙ = 1 AU. To calculate the ratio d/d⊙, we must express both distances in the same units. There are 206,265 AU in 1 pc, so we can write the distance to ε Eridani as d = (3.23 pc)(206,265 AU/pc) = 6.66 × 105 AU. Hence, the ratio of distances is d/d⊙ = (6.66 × 105 AU)/(1 AU) = 6.66 × 105. Then we find that the ratio of the luminosity of ε Eridani (L) to the Sun’s luminosity (L⊙) is
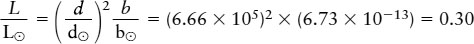
Review: This result means that ε Eridani is only 0.30 as luminous as the Sun; that is, its power output is only 30% as great.
EXAMPLE: Suppose star 1 is at half the distance of star 2 (that is, d1/d2 = ½) and that star 1 appears twice as bright as star 2 (that is, b1/b2 = 2). How do the luminosities of these two stars compare?
Situation: For these two stars, we are given the ratio of distances (d1/d2) and the ratio of apparent brightnesses (b1/b2). Our goal is to find the ratio of their luminosities (L1/L2).
Tools: Since we are comparing two stars, neither of which is the Sun, we use the second of the two equations above: L1/L2 = (d1/d2)2(b1/b2).
Answer: Plugging values into our equation, we find
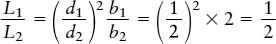
Review: This result says that star 1 has only one-half the luminosity of star 2. Despite this, star 1 appears brighter than star 2 because it is closer to us.
The two equations above are also useful in the method of spectroscopic parallax, which we discuss in Section 17-8. It turns out that a star’s luminosity can be determined simply by analyzing the star’s spectrum. If the star’s apparent brightness is also known, the star’s distance can be calculated. The inverse-square law can be rewritten as an expression for the ratio of the star’s distance from Earth (d) to the Earth-Sun distance (d⊙):

We can also use this formula as a relation between the properties of any two stars, 1 and 2:
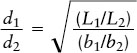
EXAMPLE: The star Pleione in the constellation Taurus is 190 times as luminous as the Sun but appears only 3.19 × 10−13 as bright as the Sun. How far is Pleione from Earth?
Situation: We are told the ratio of Pleione’s luminosity to that of the Sun (L/L⊙ = 190) and the ratio of their apparent brightnesses (b/b⊙ = 3.19 × 10−13). Our goal is to find the distance d from Earth to Pleione.
Tools: Since we are comparing Pleione to the Sun, we use the first of the two equations above.
Answer: Our equation tells us the ratio of the Earth-Pleione distance to the Earth-Sun distance:
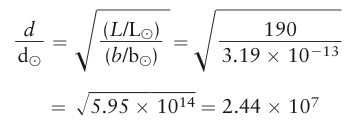
Hence, the distance from Earth to Pleione is 2.44 × 107 times greater than the distance from Earth to the Sun. The Sun-Earth distance is d⊙ = 1 AU and 206,265 AU = 1 pc, so we can express the star’s distance as d = (2.44 × 107 AU) × (1 pc/206,265 AU) = 118 pc.
Review: We can check our result by comparing it with the above example about the star ε Eridani. Pleione has a much greater luminosity than ε Eridani (190 times the Sun’s luminosity versus 0.30 times), but Pleione appears dimmer than ε Eridani (3.19 × 10−13 times as bright as the Sun compared to 6.73 × 10−13 times). For this to be true, Pleione must be much farther away from Earth than is ε Eridani. This is just what our results show: d = 118 pc for Pleione compared to d = 3.23 pc for ε Eridani.
EXAMPLE: The star δ (delta) Cephei, which lies 300 pc from Earth, is thousands of times more luminous than the Sun. Thanks to this great luminosity, stars like δ Cephei can be seen in galaxies millions of parsecs away. As an example, the Hubble Space Telescope has detected stars like δ Cephei within the galaxy NGC 3351, which lies in the direction of the constellation Leo. These stars appear only 9 × 10−10 as bright as δ Cephei. What is the distance to NGC 3351?
Situation: To determine the distance we want, we need to find the distance to a star within NGC 3351. We are told that certain stars within this galaxy have the same luminosity as δ Cephei but appear only 9 × 10−10 as bright.
Tools: We use the equation  to relate two stars, one within NGC 3351 (call this star 1) and the identical star δ Cephei (star 2). Our goal is to find d1.
to relate two stars, one within NGC 3351 (call this star 1) and the identical star δ Cephei (star 2). Our goal is to find d1.
Answer: Since the two stars are identical, they have the same luminosity (L1 = L2, or L1/L2 = 1). The brightness ratio is b1/b2 = 9 × 10−10, so our equation tells us that
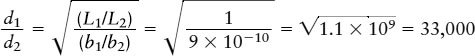
Hence, NGC 3351 is 33,000 times farther away than δ Cephei, which is 300 pc from Earth. The distance from Earth to NGC 3351 is therefore (33,000)(300 pc) = 107 pc, or 10 megaparsecs (10 Mpc).
Review: This example illustrates one technique that astronomers use to measure extremely large distances. We will learn more about stars like δ Cephei in Chapter 19, and in Chapter 23 we will explore further how they are used to determine the distances to remote galaxies.
CALCULATION CHECK 17-3
The star Pleione in the constellation Taurus is 190 times as luminous as the Sun but appears only 3.19 × 10−13 as bright as the Sun. How many times farther is Pleione from Earth compared to the Earth-Sun distance?
Pleione’s luminosity relative to that of the Sun is L/L⊙ = 190. The ratio of their apparent brightnesses is b/b⊙ = 3.19 × 10−13. Rearranging the equation relating luminosity, distance, and brightness yields the distance from Earth to Pleione as 2.44 × 107 times greater than the distance from Earth to the Sun:
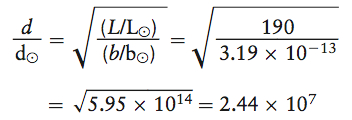
The Stellar Population
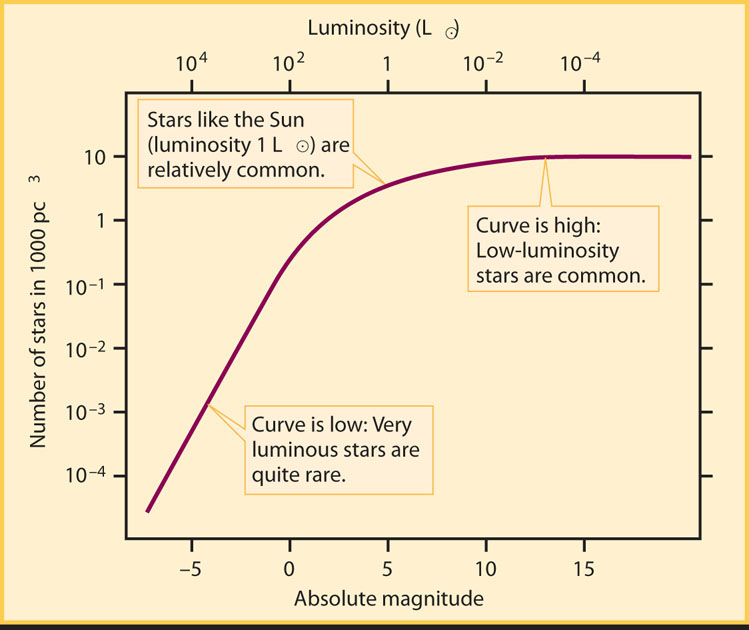
Calculations of this kind show that stars come in a wide variety of different luminosities, with values that range from about 106 L⊙ (a million times the Sun’s luminosity) to only about 10−4 L⊙ (a mere ten-thousandth of the Sun’s light output). The most luminous star emits roughly 1010 times more energy each second than the least luminous! (To put this number in perspective, about 1010 human beings have lived on Earth since our species first evolved.)
As stars go, our Sun is neither extremely luminous nor extremely dim; it is a rather ordinary, garden-variety star. It is somewhat more luminous than most stars, however. Of more than 30 stars within 4 pc of the Sun (see Appendix 4), only 3 (α Centauri, Sirius, and Procyon) have a greater luminosity than the Sun.
To better characterize a typical population of stars, astronomers count the stars out to a certain distance from the Sun and plot the number of stars that have different luminosities. The resulting graph is called the luminosity function. Figure 17-5 shows the luminosity function for stars in our part of the Milky Way Galaxy. The curve declines very steeply for the most luminous stars toward the left side of the graph, indicating that they are quite rare. For example, this graph shows that stars like the Sun are about 10,000 times more common than stars like Spica (which has a luminosity of 2100 L⊙).
The exact shape of the curve in Figure 17-5 applies only to the vicinity of the Sun and similar regions in our Milky Way Galaxy. Other locations have somewhat different luminosity functions. In stellar populations in general, however, low-luminosity stars are much more common than high-luminosity ones.