20-4 The burned-out core of a moderately low-mass star cools and contracts until it becomes a white dwarf

We have seen that after a moderately low-mass star (from about 0.4 to about 4 solar masses) consumes all the hydrogen in its core, it is able to ignite nuclear reactions that convert helium to carbon and oxygen. Given sufficiently high temperature and pressure, carbon and oxygen can also undergo fusion reactions that release energy. But for such a moderately low-mass star, the core temperature and pressure never reach the extremely high values needed for these reactions to take place. Instead, as we have seen, the process of mass ejection just strips away the star’s outer layers and leaves behind the hot carbon-oxygen core. With no nuclear reactions taking place, the core simply cools down like a dying ember. This burned-out relic of a star’s former glory is called a white dwarf. Such white dwarfs prove to have exotic physical properties that are wholly unlike any object found on Earth.

Properties of White Dwarfs

You might think that without nuclear reactions to provide internal heat and pressure, a white dwarf should keep on shrinking under the influence of its own gravity as it cools. Actually, a cooling white dwarf maintains its size, because the burned-out stellar core is so dense that most of its electrons are degenerate (see Section 19-3). Thus, degenerate electron pressure supports the star against further collapse. This pressure does not depend on temperature, so it continues to hold up the star even as the white dwarf cools and its temperature drops.

Many white dwarfs are found in the solar neighborhood, but all are too faint to be seen with the naked eye. One of the first white dwarfs to be discovered is a companion to Sirius, the brightest star in the night sky. In 1844 the German astronomer Friedrich Bessel noticed that Sirius was moving back and forth slightly, as if it was being orbited by an unseen object. This companion, designated Sirius B (Figure 20-9), was first glimpsed in 1862 by the American astronomer Alvan Clark. Recent Hubble Space Telescope observations at ultraviolet wavelengths, where hot white dwarfs emit most of their light, show that the surface temperature of Sirius B is 25,200 K. (By contrast, the main-sequence star Sirius A has a surface temperature of 10,500 K, while the Sun’s surface temperature is a relatively frosty 5800 K.)

Figure 20-9: R I V U X G
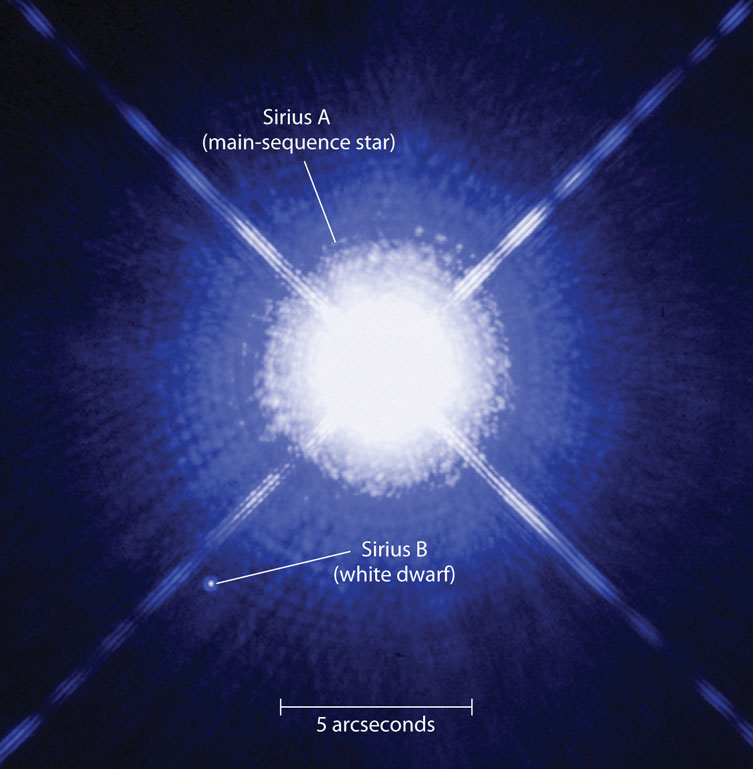
Sirius A and Its White Dwarf Companion Sirius, the brightest-appearing star in the sky, is actually a binary star: The secondary star, called Sirius B, is a white dwarf. In this Hubble Space Telescope image, Sirius B is almost obscured by the glare of the overexposed primary star, Sirius A, which is about 10⁴ times more luminous than Sirius B. The halo and rays around Sirius A are the result of optical effects within the telescope.

(NASA; H. E. Bond and E. Nelan, STScI; M. Barstow and M. Burleigh, U. of Leicester; and J. B. Holberg, U. of Arizona)

The Density of White Dwarfs

Observations of white dwarfs in binary systems like Sirius allow astronomers to determine the mass, radius, and density of these stars (see Sections 17-9, 17-10, and 17-11). Such observations show that the density of the degenerate matter in a white dwarf is typically 10⁹ kg/m³ (a million times denser than water). A teaspoonful of white dwarf matter brought to Earth would weigh nearly 5.5 tons—as much as an elephant!

Compressing matter so that an elephant could fit into a teaspoon might seem impossible until you remember that most of an atom is empty space. We mentioned in Section 5-7 that if you imagine a typical atom expanded to the size of a football field, the nucleus at the 50-yard line would only be 1 cm wide. That leaves a lot of space between the nucleus and its electrons that would be out near the goal posts; even farther out would be the nucleus of the next nearest atom. The incredible density of a white dwarf leaves much less empty space between its atoms, but as we will see, objects called neutron stars are even denser than white dwarfs.

The Mass-Radius Relation for White Dwarfs

Figure 20-10: The Mass-Radius Relationship for White Dwarfs The more massive a white dwarf is, the smaller its radius. (The drawings of white dwarfs of different mass are drawn to the same scale as the image of Earth.) This unusual relationship is a result of the degenerate-electron pressure that supports the star. The maximum mass of a white dwarf, called the Chandrasekhar limit, is 1.4 M_⊙.

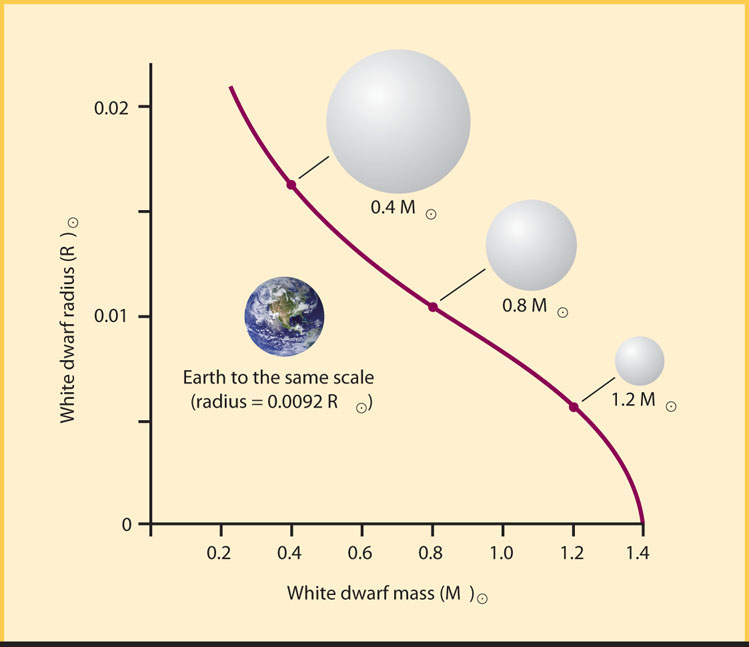
As we learned in Section 19-3, degenerate matter has a very different relationship between its pressure, density, and temperature than that of ordinary gases. Consequently, white dwarf stars have an unusual mass-radius relation: The more massive a white dwarf star, the smaller it is. Figure 20-10 displays the mass-radius relation for white dwarfs. Note that the more degenerate matter you pile onto a white dwarf, the smaller it becomes. However, there is a limit to how much pressure degenerate electrons can produce. As a result, there is an upper limit to the mass that a white dwarf can have. This maximum mass is called the Chandrasekhar limit, after the Indian-American scientist Subrahmanyan Chandrasekhar, who pioneered theoretical studies of white dwarfs in the 1930s. (The orbiting Chandra X-ray Observatory, described in Section 6-7, is named in his honor.) The Chandrasekhar limit is equal to 1.4 M_⊙, meaning that all white dwarfs must have masses less than 1.4 M_⊙. As we will see in Section 20-6, when the Chandrasekhar limit is exceeded, the star is no longer a white dwarf, and the results are explosive.

It is worth pointing out that the Chandrasekhar limit represents a huge scientific success. Electron degeneracy pressure is based on the quantum physics of electrons on the smallest of imaginable scales, yet the Chandrasekhar limit applies this physics to a solar mass of material about the size of Earth. Observations verify that white dwarfs do not exceed the Chandrasekhar limit: Numerous white dwarfs are in binary systems (that allows their masses to be measured; see Section 4-7), and amazingly, none are above 1.4 M_⊙!

The material inside a white dwarf consists mostly of ionized carbon and oxygen atoms floating in a sea of degenerate electrons. As the dead star cools, the carbon and oxygen ions slow down, and electric forces between the ions begin to prevail over the random thermal motions. About 5 × 10⁹ years after the star first becomes a white dwarf, when its luminosity has dropped to about 10⁻⁴ L_⊙ and its surface temperature is a mere 4000 K, the ions no longer move freely. Instead, they arrange themselves in orderly rows, like an immense crystal lattice. From this time on, you could say that the star is “solid.” The degenerate electrons move around freely in this crystalline material, just as electrons move freely through an electrically conducting metal like copper or silver. A diamond is also crystalline (with carbon ordered in a crystal lattice), so a cool carbon-oxygen white dwarf has some similarities to a giant diamond in the sky!

From Red Giant to Planetary Nebula to White Dwarf

Figure 20-11 shows the evolutionary tracks followed by three burned-out stellar cores as they pass through the planetary nebula stage and become white dwarfs. When these three stars were red giants, they had masses of 0.8, 1.5, and 3.0 M_⊙. Mass ejection strips these dying stars of up to 60% of their matter. During their final spasms, the luminosity and surface temperature of these stars change quite rapidly. The points representing these stars on an H-R diagram race along their evolutionary tracks, sometimes executing loops corresponding to thermal pulses (see Track B and Track C in Figure 20-11). Finally, as the ejected nebulae fade and the stellar cores cool, the evolutionary tracks of these dying stars take a sharp turn toward the white dwarf region of the H-R diagram. As the table accompanying Figure 20-11 shows, the final white dwarf has only a fraction of the mass of the giant star from which it evolved.

Figure 20-11: Evolution from Giants to White Dwarfs This H-R diagram shows the evolutionary tracks of three low-mass giant stars as they eject planetary nebulae. The table gives the extent of mass loss in each case. The dots represent the central stars of planetary nebulae whose surface temperatures and luminosities have been determined; the crosses represent white dwarfs of known temperature and luminosity.

(Adapted from B. Paczynski)

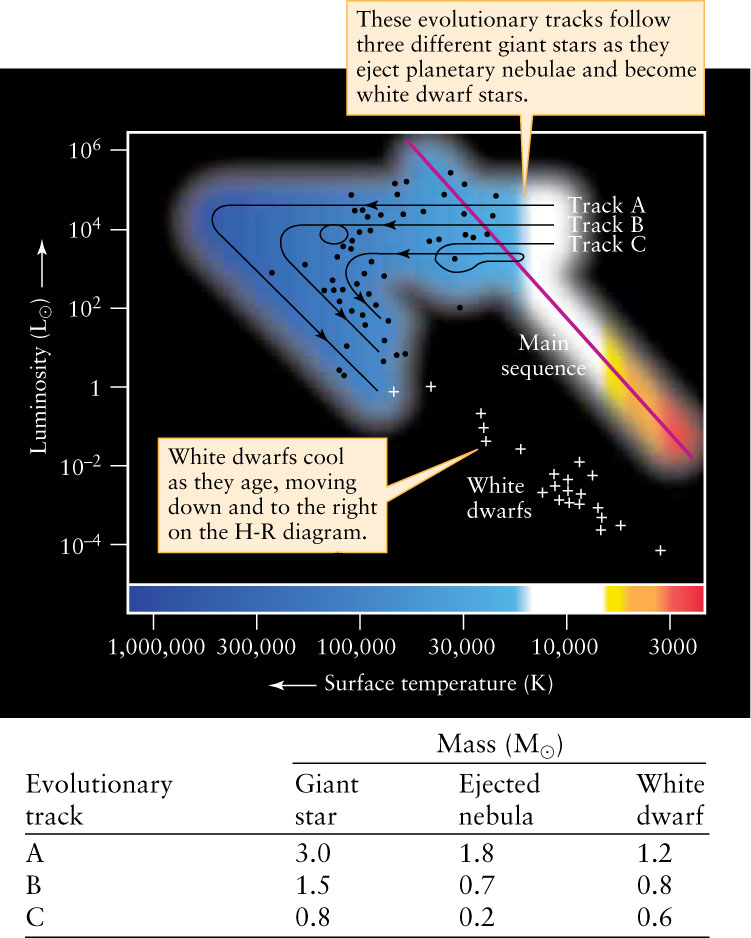
Although a white dwarf maintains the same size as it cools, its luminosity and surface temperature both decrease with time. Consequently, the evolutionary tracks of aging white dwarfs point toward the lower right corner of the H-R diagram. You can see this in the lower right portion of Figure 20-11. After ejecting much of its mass into space, our own Sun will eventually evolve into a white dwarf star about the size of Earth and with perhaps one-tenth of its present luminosity. It will become even dimmer as it cools. After 5 billion years as a white dwarf, the Sun will radiate with no more than one ten-thousandth of its present brilliance. With the passage of eons, our Sun will simply fade into obscurity. The Cosmic Connections figure summarizes the full evolutionary cycle of a 1-M_⊙ star like the Sun, from its birth as a main-sequence star to its demise as a white dwarf.