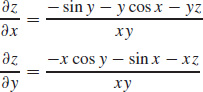Chapter 12

Section 12.1

1.

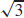
2. True

3. x, y, z; w

4. True

5. (a) 2

(b) 10

(c) 3x + 3(Δx) + 2y + xy + (Δx)y

(d) 3x + 2y + 2(Δy) + xy + x(Δy)

7. (a) 0

(b) at + a²

(c)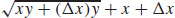

(d)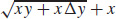

9. (a) 1

(b) 0

(c) 3 sin t cos t

11. (a) 0

(b) 2

(c) 92

13. {(x, y) | x ≥ 0, y > 0}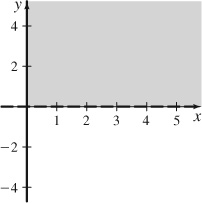

15. {(x, y) |x, y ≥ 0 or x, y ≤ 0}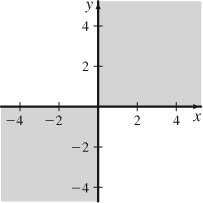

17. {(x, y) | x is any real number, y is any real number}

19. {(x, y) |x² − y² > 0}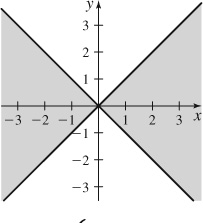

21. {(x, y) |2y + x² > 0}

23. {(x, y) | x² + y² < 9}

25. {(x, y, z) | z ≠ 0}

27.

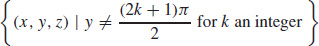
29.

31.

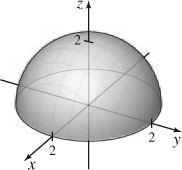
33.

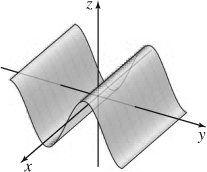
35.

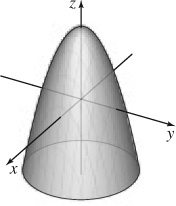
37.

39. (a)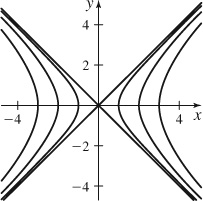

(b)

41. (a)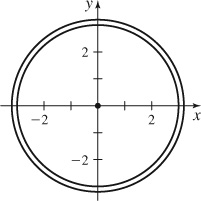

(b)

43. (a)

(b)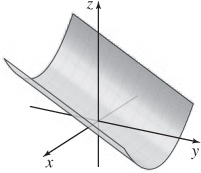

45. (a)

(b)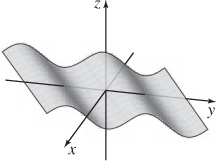

47. (a) Answers will vary.

(b) Answers will vary.

(c) Answers will vary.

49. (a) Answers will vary.

(b) Answers will vary.

(c) Answers will vary.

51. (a) Answers will vary.

(b) Answers will vary.

(c) Answers will vary.

53. F

55. B

57. A

59. (a) 47°F

(b) As you move south, the temperature change is increasing.

(c) If you wanted to move as quickly as possible to the next warmer temperature zone, you would move toward the southwest.

(d) Answers will vary.

61. (a) ≈83

(b) 120

(c) ≈14

63. (a) 6.75

(b) 18

(c) 2

(d) 1.5

65. (a) ≈104.715°F

(b) ≈43.830%

67. S(x, y, z) = xy + 2xz + 2yz

69. C(x, y, z) = 4xy + 6xz + 4yz

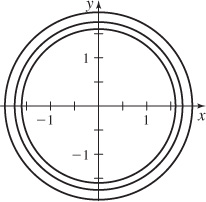
71.

73. Level surfaces for E(x, y, z) are all cylinders of differing radii unbounded in the x-direction.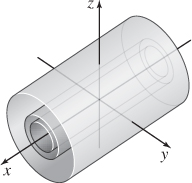

75. (a) Answers will vary.

(b) Answers will vary.

(c) Answers will vary.

77. (a) Answers will vary.

(b) Answers will vary.

79. (a)

(b) Answers will vary.

(c)

(d)

(e) Answers will vary.

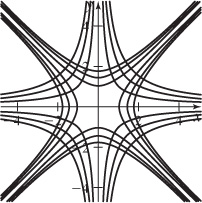
81.

83. These inequalities describe the set of points that are inside the sphere of radius 1 centered at the origin, and inside the upper half of the elliptic cone x² + y² = z², not including the boundary.

Section 12.2

1. (c)

2. 16

3. False

4. True

5. (c)

6. (a)

7. False

8. 1

9. 7

11. −1

13. −1

15.

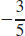
17.

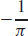
19. −3

21. 0

23.

25. (a) 0

(b) 0

(c) 1

(d)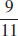

(e) 0. This limit does not exist.

27. (a) 0

(b) 0

(c) 0

(d) 0

(e) 0. No conclusion can be reached.

29. (a) 0

(b) 0

(c)

(d)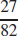

(e) 0. This limit does not exist.

31. (a) 1

(b) 0

(c) 1

(d)

(e) 1. This limit does not exist.

33. See Student Solutions Manual.

35. See Student Solutions Manual.

37. This function is continuous for all points (x, y) in the plane.

39. This function is continuous for all points (x, y) in the plane except on the line y = x.

41. This function is continuous for all points (x, y) in the plane.

43. This function is continuous for all points (x, y) in the plane.

45. This function is continuous for all points (x, y) in the plane.

47. This function is continuous for all points (x, y) in the plane.

49. 1

51. 1

53. 0

55.

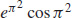
57.

59. 1

61.

63. See Student Solutions Manual.

65. (a) The function is discontinuous at (0, 0).

(b) Yes, it is possible to define f (x, y) at (0, 0).

(c) 0

67. (a) The function is discontinuous at (0, 0).

(b) No, it is not possible to define f (x, y) at (0, 0).

69. (a) The function is discontinuous at (0, 0).

(b) No, it is not possible to define f (x, y) at (0, 0).

71. (a) The function is continuous at (0, 0).

73. 0

75. This limit does not exist.

77. 5

Section 12.3

1. False

2. (b)

3. True

4. Mixed

5. False

6. x; z; y

7. f_x (x, y) = 2xy; f_y(x, y) = x² + 12y

9.

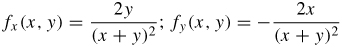
11. f_x (x, y) = −e^y sin x + e^x sin y; f_y(x, y) = e^y cos x + e^x cos y

13. f_x (x, y) = 2xe^xy+x²ye^xy; f_y(x, y) = x³e^xy

15.

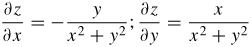
17.

19.

21. f_xx = 12; f_xy = −8; f_yx = −8; fyy = 18

23.

25. f_xx = −4x² y⁶ cos(x² y³) − 2y³ sin(x² y³); f_xy = −6x³ y⁵ cos(x² y³) − 6xy² sin(x² y³); f_yx = −6x³ y⁵ cos(x² y³) − 6xy² sin(x² y³); f_yy = −9x⁴ y⁴ cos(x² y³) − 6x² y sin(x² y³)

27. f_x (x, y, z) = y + z; f_y(x, y, z) = x + z; f_z(x, y, z) = x + y

29. f_x (x, y, z) = y sin z − yz cos x; f_y(x, y, z) = x sin z − z sin x; f_z(x, y, z) = xy cos z − y sin x

31.

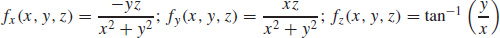
33.

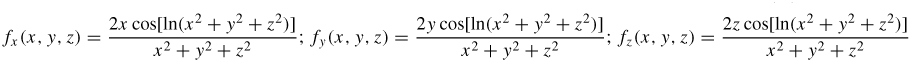
35. f_x(0, 0) = 1; f_y(0, 0) = 1

37.

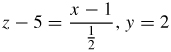
39.

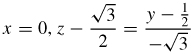
41.

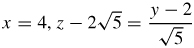
43. (a)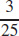

(b)

45. (a) See Student Solutions Manual.

(b) . For every unit increase in the direction of the positive x-axis from the point (1, 2), there is an increase in the temperature of the plate of approximately 58°C, and from (2, 1) the increase is approximately 115°C.

(c) 0; 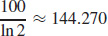. For every unit increase in the direction of the positive y-axis from the point (2, 0), there is approximately no increase in the temperature of the plate, and from (0, 2) the increase is approximately 144°C.

47. See Student Solutions Manual.

49. (a)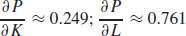

(b)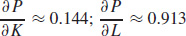

(c) Answers will vary.

51.

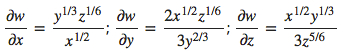
53. See Student Solutions Manual.

55.

57. (a)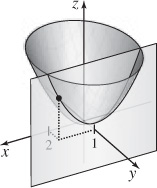

(b) 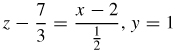, y = 1

59. See Student Solutions Manual.

61. See Student Solutions Manual.

63. See Student Solutions Manual.

65. See Student Solutions Manual.

67. See Student Solutions Manual.

69. See Student Solutions Manual.

71. See Student Solutions Manual.

73. See Student Solutions Manual.

75. (a)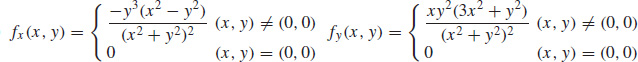

(b) See Student Solutions Manual.

77. No; answers will vary.

79. See Student Solutions Manual.

81. See Student Solutions Manual.

83. See Student Solutions Manual.

85.

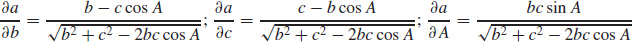
87. f_x = x^y−1 y; f_y = x^y ln x

89. 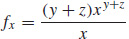; f_y = x^y+z ln x; f_z = x^y+z ln x

91. f_x = (x + y)^z−1z; f_y = (x + y)^z−1z; f_z = (x + y)^z ln(x + y)

93. f_x(0, 0) = 0; f_y(0, 0) = 0

95. See Student Solutions Manual.

97. See Student Solutions Manual.

99. (a) f_x(1, 6) = 6; f_y(1, 6) = 432

(b)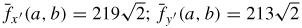

Section 12.4

1. True

2. True

3. True

4. True

5. True

6. False

7. Δz = 1.45

9. Δz ≈ −0.318

11. dz = (2x) dx + (2y) dy

13. dz = (sin y + y cos x) dx + (x cos y + sin x) dy

15.

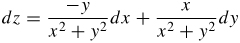
17.

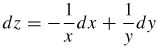
19. dz = ye^xydx + xe^xydy

21.

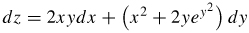
23. dw = (e^yz + yze^xz + yze^xy) dx + (xze^yz + e^xz + xze^xy) dy + (xye^yz + xye^xz + e^xy) dz

25.

27. dw = (yz) dx + (xz) dy + (xy) dz

29. (a) Δz = (y² − 2y)Δx + (2xy − 2x)Δy + (2yΔy − 2Δy)Δx + (xΔy + ΔxΔy)Δy

(b) η₁ = 2yΔy − 2Δy; η₂ = xΔy + ΔxΔy

(c) See Student Solutions Manual.

31. (a)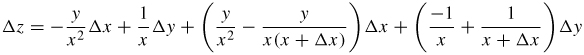

(b)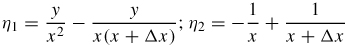

(c) See Student Solutions Manual.

33. (a) Δz ≈ dz = 1.4

(b) Δz = 1.45

35. (a) dz ≈ −0.324

(b) Δz ≈ −0.318

37. The area of the triangle increases by ≈0.225 cm²

39. (a) ≈0.016 cm³

(b) ≈0.126 cm²

41. ≈15%

43. ≈3.02%

45. (a) 2.173 g/cm³

(b) 16%

47. (a)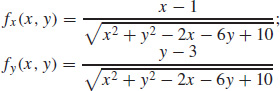

(b) The partial derivatives are continuous for all points (x, y) as long as (x, y) ≠ (1, 3).

(c)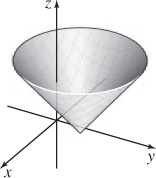

(d) Answers will vary.

49. See Student Solutions Manual.

51. See Student Solutions Manual.

53. (a) ≈0.5758Ω

(b) ≈15.516%

(c) The increase in the resistivity

Section 12.5

1. False

2. False

3.

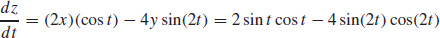
5.

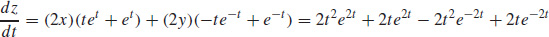
7.

9.

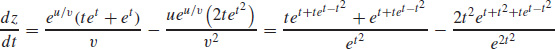
11.

13.

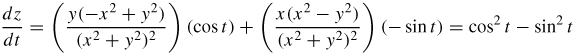
15.

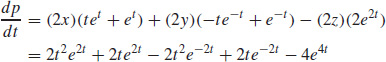
17.

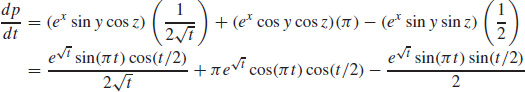
19.

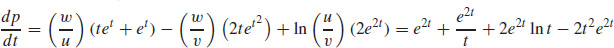
21.

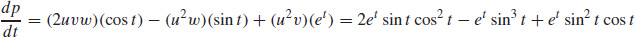
23.

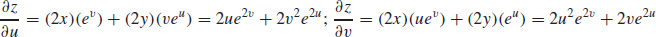
25.

27.

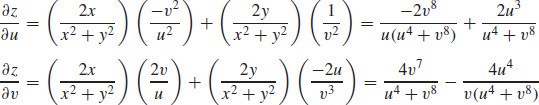
29.

31.

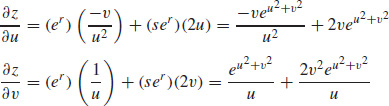
33.

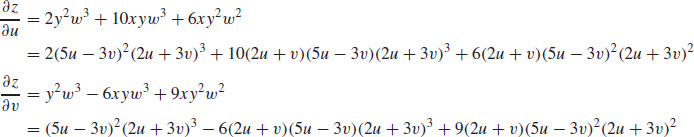
35.

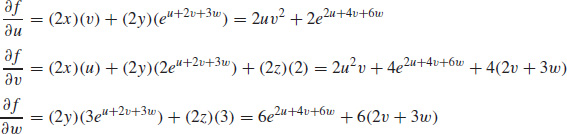
37.

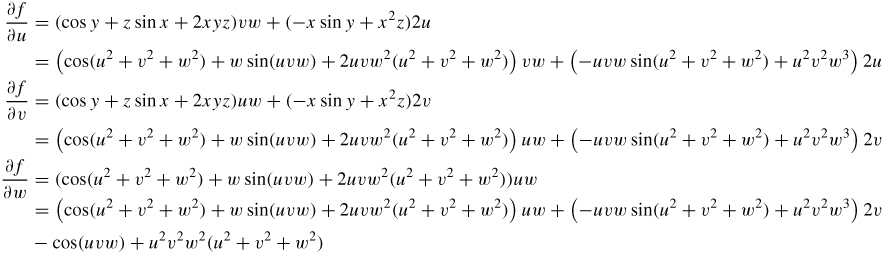
39.

41.

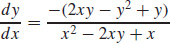
43.

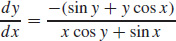
45.

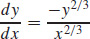
47.

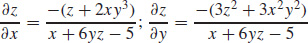
49.

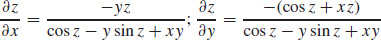
51.

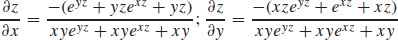
53.

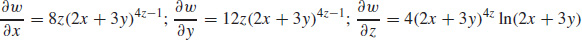
55. 13.2 m³/s

57. (a) See Student Solutions Manual.

(b) See Student Solutions Manual.

(c) See Student Solutions Manual.

(d) See Student Solutions Manual.

59.

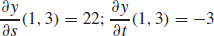
61.

63. See Student Solutions Manual.

65. See Student Solutions Manual.

67. See Student Solutions Manual.

69. See Student Solutions Manual.

71. (a) See Student Solutions Manual.

(b)

Review Exercises

1. (a) 0

(b) e^x+Δx ln y

(c) e^x ln(y + Δy)

3. (a)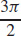

(b)

(c) 0

5. {(x, y) | x² + 4y² ≤ 9}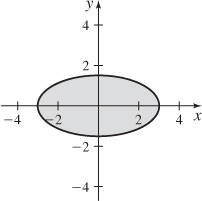

7.

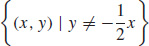
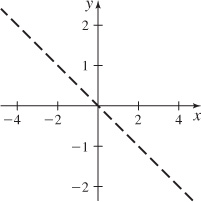
9. {(x, y, z) | z > 0}

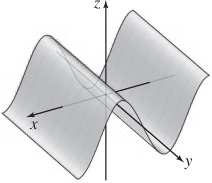
11.

13.

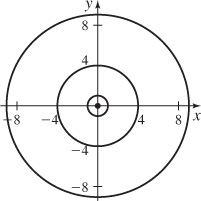
15.

17. The level surfaces associated with the function w = 4x² + y² + z² are ellipsoids and the point (0, 0, 0).

19.

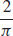
21. (a) See Student Solutions Manual.

(b)

(c) This limit does not exist.

23. The function is continuous at all points (x, y) in the plane.

25. (a) This function is continuous at all points (x, y) in the plane except the origin, (0, 0).

(b)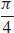

27.

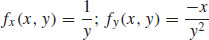
29.

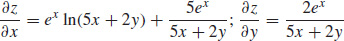
31.

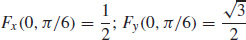
33. (a) y = −2,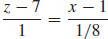

(b) x = 1,

35. f_xx (x, y) = 6e^3x + 9(x + y²)e^3x; f_xy(x, y) = 6ye^3x; f_yx (x, y) = 6ye^3x; f_yy(x, y) = 2e^3x

37. f_x = yze^xyz; f_y = xze^xyz; f_z = xye^xyz

39. f_x = e^x sin y; f_y = e^x cos y + e^y sin z; f_z = e^y cos z

41. See Student Solutions Manual.

43. (a) Δz = (y)Δx + (x − 10y)Δy + (Δy)Δx + (−5Δy)Δy

(b) η₁ = Δy; η₂ = −5Δy

(c) See Student Solutions Manual.

45.

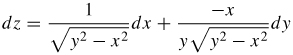
47.

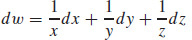
49. \(\Delta z\) ≈ 0.1

51. The approximate maximum percentage error is 3%.

53.

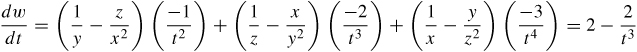
55.

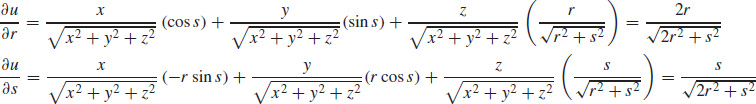
57.