6.2 Volume of a Solid of Revolution: Disks and WashersPrinted Page 413
OBJECTIVES
When you finish this section, you should be able to:
- Use the disk method to find the volume of a solid formed by revolving a region about the \(x\)-axis (p. 415)
- Use the disk method to find the volume of a solid formed by revolving a region about the \(y\)-axis (p. 416)
- Use the washer method to find the volume of a solid formed by revolving a region about the \(x\)-axis (p. 418)
- Use the washer method to find the volume of a solid formed by revolving a region about the \(y\)-axis (p. 420)
- Find the volume of a solid formed by revolving a region about a line parallel to a coordinate axis (p. 421)
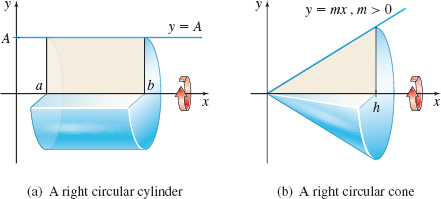
An example of a solid of revolution is the right circular cylinder, which is generated by revolving the region bounded by a horizontal line \(y=A, A > 0\), the \(x\)-axis, and the lines \(x=a\) and \(x=b\) about the \(x\)-axis. See Figure 14(a). Another familiar example of a solid of revolution, pictured in Figure 14(b), is a right circular cone that is generated by revolving the region in the first quadrant bounded by a line \(y=mx, m > 0\), the \(x\)-axis, and the line \(x=h\) about the \(x\)-axis.
Although the volume of these simple solids of revolution can be found using geometry formulas, to find the volume of most solids of revolution requires the use of calculus.
414
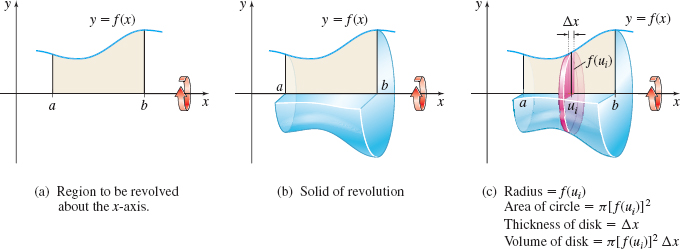
Consider a region that is bounded by the graph of a function \(y=f(x)\) that is continuous and nonnegative on the interval \([a,b]\), the \(x\)-axis, and the lines \(x=a\) and \(x=b\). See Figure 15(a). Suppose this region is revolved about the \(x\)-axis. The result is a solid of revolution. See Figure 15(b).
To find the volume of a solid of revolution, we begin by partitioning the interval \([a,b]\) into \(n\) subintervals: \begin{equation*} \lbrack a, x_{1}], [x_{1}, x_{2}], \ldots , [x_{i-1}, x_{i}] , \ldots , [x_{n-1}, b] \end{equation*}
each of width \(\Delta x=\dfrac{b-a}{n}\) and selecting a number \(u_{i}\) in each subinterval. Refer to Figure 15(c). The circle obtained by slicing the solid at \(u_{i}\) has radius \(r_{i}= f(u_{i})\) and area \(A_{i}=\pi r_{i}^{2}=\pi \lbrack f(u_{i})]^{2}\). The volume \(V_{i}\) of the disk obtained from the \(i\)th subinterval is \(V_{i}=\pi [f(u_{i})]^{2}\Delta x\), and an approximation to the volume \(V\) of the solid of revolution is \begin{equation*} V\approx \pi \sum\limits_{i=1}^{n}\, [f(u_{i})]^{2}~\Delta x \end{equation*}
IN WORDS
The volume \(V\) of a disk is \begin{array}{rcl} V &=& \hbox{(Area of the circular cross section)}\\[3pt] &&\times\,\hbox{(Thickness)}\\[3pt] &=&\pi (\hbox{Radius})^{2} (\hbox{Thickness}) \end{array}
As the number \(n\) of subintervals increases, the sums \(\pi \sum\limits_{i=1}^{n}[f(u_{i})]^{2}\Delta x\) become better approximations to the volume \(V\) of the solid, and \begin{equation*} V=\pi \lim\limits_{n\,\rightarrow \,\infty }\sum_{i=1}^{n}\,[f(u_{i})]^{2}~\Delta x \end{equation*}
These sums are Riemann sums. So if \(f\) is continuous on the interval \([a,b]\), then the limit is a definite integral and \begin{equation*} V=\pi \int_{a}^{b}\left[ f(x) \right] ^{2}\,{\it dx} \end{equation*}
NEED TO REVIEW?
Riemann sums and the definite integral are discussed in Section 5.2, pp. 353-359.
This approach to finding the volume of a solid of revolution is called the disk method.
Volume of a Solid of Revolution Using the Disk Method
If a function \(f\) is continuous and nonnegative on a closed interval \([a,b]\), then the volume \(V\) of the solid of revolution obtained by revolving the region bounded by the graph of \(f\), the \(x\)-axis, and the lines \(x=a\) and \(x=b\) about the \(x\)-axis is \begin{equation*} \bbox[5px, border:1px solid black, #F9F7ED] { V=\pi \int_{a}^{b}[f(x)]^{2}~{\it dx} } \end{equation*}
1 Use the Disk Method to Find the Volume of a Solid Formed by Revolving a Region About the \(x\)-AxisPrinted Page 415
415
EXAMPLE 1Using the Disk Method: Revolving About the \(x\)-Axis
Find the volume of the solid of revolution generated by revolving the region bounded by the graph of \(y=\sqrt{x}\), the \(x\)-axis, and the line \(x=5\) about the \(x\)-axis.
Solution We begin by graphing the region to be revolved. See Figure 16(a). Figure 16(b) shows a typical disk and Figure 16(c) shows the solid of revolution. Using the disk method, the volume \(V\) of the solid of revolution is \[ V=\pi \int_{0}^{5}( \sqrt{x}) ^{2}~{\it dx}=\pi \int_{0}^{5} x~{\it dx}= \pi \!\left[\dfrac{x^{2}}{2}\right] _{0}^{5}=\dfrac{25}{2} \pi \hbox{ cubic units} \]
NOW WORK
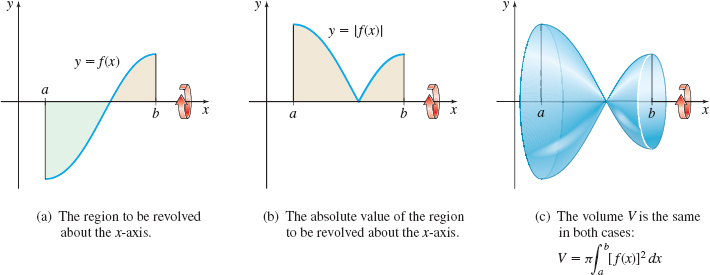
The disk method does not require the function \(f\) to be nonnegative. As Figure 17 illustrates, the volume \(V\) of the solid of revolution obtained by revolving about the \(x\)-axis the region bounded by the graph of a function \(f\) that is continuous on the interval \([a,b]\), the \(x\)-axis, and the lines \(x=a\), and \(x=b\) equals the volume of the solid of revolution obtained by revolving about the \(x\)-axis the region bounded by the graph of \(y=\left\vert f\,(x)\right\vert\), the \(x\)-axis, and the lines \(x=a\) and \(x=b\). Since \(\left\vert \,f\,(x)\right\vert ^{2}=[f(x)]^{2}\), the formula for \(V\) does not change.
416
EXAMPLE 2Using the Disk Method: Revolving About the \(x\)-Axis
Find the volume of the solid of revolution generated by revolving the region bounded by the graph of \(y=x^{3}\), the \(x\)-axis, and the lines \(x=-1\) and \(x=2\) about the \(x\)-axis.
Solution Figure 18(a) shows the graph of the region to be revolved about the \(x\)-axis. Figure 18(b) illustrates a typical disk and Figure 18(c) shows the solid of revolution.
Using the disk method, the volume \(V\) of the solid of revolution is \begin{equation*} V=\pi \int_{-1}^{2}x^{6}{\it dx}=\pi \left[ \frac{x^{7}}{7}\right] _{-1}^{2}=\frac{ \pi }{7}(128+1)=\frac{129}{7}\pi \hbox{ cubic units} \end{equation*}
NOW WORK
2 Use the Disk Method to Find the Volume of a Solid Formed by Revolving a Region About the \(y\)-AxisPrinted Page 416
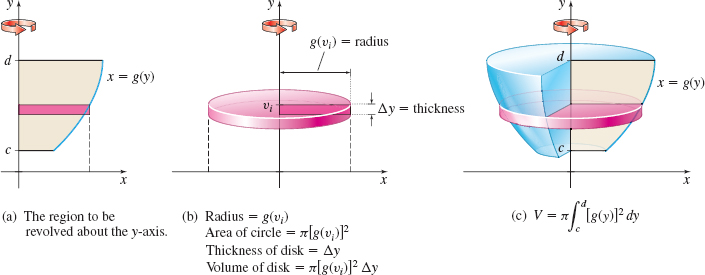
A solid of revolution can be generated by revolving a region about any line. In particular, the volume \(V\) of the solid of revolution generated by revolving the region bounded by the graph of \(x=g(y)\), where \(g\) is continuous and nonnegative on the closed interval \([c,d]\), the \(y\)-axis, and the horizontal lines \(y=c\) and \(y=d\) about the \(y\)-axis can be obtained by partitioning the \(y\)-axis and taking slices perpendicular to the \(y\)-axis of thickness \(\Delta y\). See Figure 19(a) on page 417.
Again, the cross sections are circles, as shown in Figure 19(b). The radius of a typical cross section is \(r_{i}=g( v_{i})\), and its area \(A_{i}\) is \(A_{i}=\pi r_{i}^{2}=\pi \lbrack g(v_{i})]^{2}\). The volume of the disk of radius \(r_{i}\) and thickness \(\Delta y=\dfrac{d-c}{n}\) is \(V_{i}=\pi r_{i}^{2}\Delta y= \pi \lbrack g(v_{i})]^{2}~\Delta y\). By summing the volumes of all the disks and taking the limit, the volume \(V\) of the solid of revolution is given by \begin{equation*} \bbox[5px, border:1px solid black, #F9F7ED] { V=\pi \int_{c}^{d}[g(y)]^{2}~{\it dy}} \end{equation*}
See Figure 19(c).
417
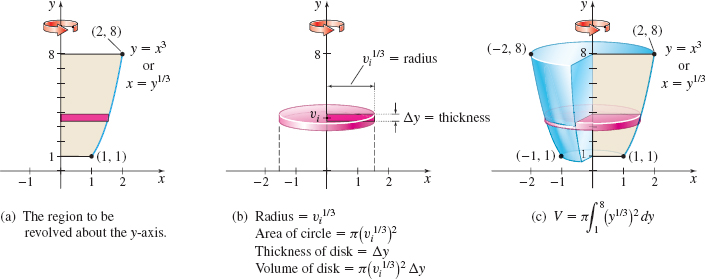
EXAMPLE 3Using the Disk Method: Revolving About the \(y\)-Axis
Use the disk method to find the volume of the solid of revolution generated by revolving the region bounded by the graph of \(y=x^{3}\), the \(y\)-axis, and the lines \(y=1\) and \(y=8\) about the \(y\)-axis.
Solution Figure 20(a) shows the region to be revolved. Since the solid is formed by revolving the region about the \(y\)-axis, we write \(y=x^{3}\) as \(x=\sqrt[3]{y}=y^{1/3}\). Figure 20(b) illustrates a typical disk, and Figure 20(c) shows the solid of revolution. Using the disk method, the volume \(V\) of the solid of revolution is \begin{eqnarray*} V&=&\pi \int_{1}^{8}[ y^{1/3}] ^{2}~{\it dy}=\pi \int_{1}^{8}y^{2/3}~{\it dy}=\pi \left[ \dfrac{y^{5/3}}{\dfrac{5}{3}}\right]_{1}^{8}\\[8pt] &=&\dfrac{3\pi }{5}(32-1)=\dfrac{93}{5}\pi \hbox{ cubic units} \end{eqnarray*}
NOW WORK
3 Use the Washer Method to Find the Volume of a Solid Formed by Revolving a Region About the \(x\)-AxisPrinted Page 418
418
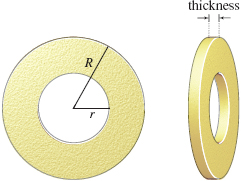
NOTE
A washer is used in joints to ensure tightness, prevent leakage, or relieve friction. Washers are used in plumbing, construction, and carpentry.
A washer is a thin flat ring with a hole in the middle. It can be represented by two concentric circles, an outer circle of radius \(R\) and an inner circle of radius \(r\), as shown in Figure 21. The volume of a washer is found by finding the area of the outer circle, \(\pi R^{2}\), subtracting the area of the inner circle, \(\pi r^{2}\), then multiplying the result by the thickness of the washer.
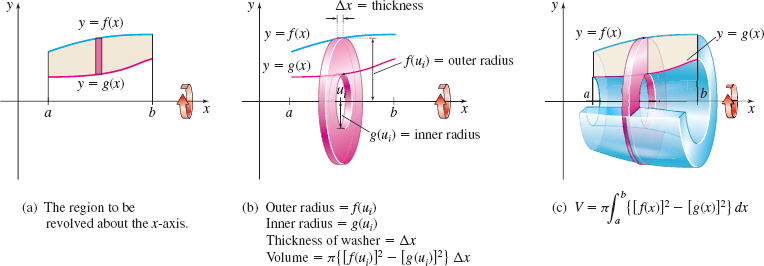
Suppose we have two functions \(y=f(x)\) and \(y=g(x), f(x) \geq g(x) \geq 0\), that are continuous on the closed interval \([a,b]\). If the region bounded by the graphs of \(f\) and \(g\) and the lines \(x=a\) and \(x=b\) is revolved about the \(x\)-axis, a solid of revolution with a hollow interior is generated, as illustrated in Figure 22. We seek a formula for finding its volume \(V\).
Figure 23(a) shows the region to be revolved about the \(x\)-axis. To find the volume \(V\) of the resulting solid of revolution using the washer method, we begin by partitioning the interval \([a,b]\) into \(n\) subintervals: \begin{equation*} \lbrack a, x_{1}], [x_{1}, x_{2}], \ldots , [x_{i-1}, x_{i}] , \ldots , [x_{n-1}, b] \end{equation*}

each of width \(\Delta x=\dfrac{b-a}{n}\). In each subinterval \([x_{i-1},x_{i}], i=1,2,\ldots ,n\), we select a number \(u_{i}\). We then slice the solid at \(x=u_{i}\). The slice is a washer that has outer radius \(R_{i}=f( u_{i})\), inner radius \(r_{i}=g(u_{i})\), and thickness \(\Delta x\). A typical washer is shown in Figure 23(b). The area \(A_{i}\) between the concentric circles that form the washer is the difference between the area of the outer circle and the area of the inner circle. \begin{equation*} A_{i}=\pi R_{i}^{2}-\pi r_{i}^{2}=\pi \lbrack f(u_{i})]^{2}-\pi [ g( u_{i}) ] ^{2}=\pi \{ [ f( u_{i}) ] ^{2}-[ g( u_{i}) ] ^{2}\} \end{equation*}
The volume \(V_{i}\) of the washer is \begin{equation*} V_{i}=A_{i}\Delta x=\pi \{ [ f(u_{i})] ^{2}-[ g(u_{i}) ] ^{2}\} \Delta x \end{equation*}
and the volume \(V\) of the solid can be approximated by \begin{equation*} V\approx \pi \sum_{i=1}^{n}\{ [ f(u_{i})] ^{2}-[g(u_{i})] ^{2}\} \Delta x \end{equation*}
As the number \(n\) of subintervals increases, the sums \(\sum\limits_{i=1}^{n}V_{i}\) become better approximations to the volume \(V\) of the solid of revolution. Since the sums are Riemann sums and since \(f\) and \(g\) are continuous, the limit as \(n\rightarrow \infty\) is a definite integral. See Figure 23(c).
IN WORDS
The volume \(V\) of a washer is \begin{eqnarray*} V&=&\pi [\hbox{(Outer radius)}^{2}- \hbox{(Inner radius)}^{2}]\\[0pt] &&\times\, \hbox{(Thickness)} \end{eqnarray*}
419
Volume of a Solid of Revolution Using the Washer Method
If the functions \(y=f(x)\) and \(y=g(x)\) are continuous on the closed interval \([a,b]\) and if \(f(x) \geq g(x) \geq 0\) on \([a,b]\), then the volume \(V\) of the solid of revolution obtained by revolving the region bounded by the graphs of \(f\) and \(g\) and the lines \(x = a\) and \(x = b\) about the \(x\)-axis is \begin{equation*} \bbox[5px, border:1px solid black, #F9F7ED]{ V=\pi \displaystyle \int_{a}^{b}\{ [f(x)] ^{2}-[ g(x)] ^{2} \}~ {\it dx}} \end{equation*}
EXAMPLE 4Using the Washer Method: Revolving About the \(x\)-Axis
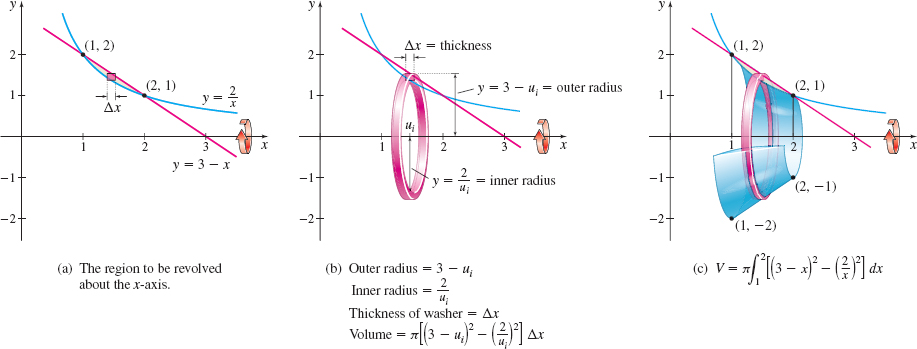
Find the volume \(V\) of the solid of revolution generated by revolving the region bounded by the graphs of \(y=\dfrac{2}{x}\) and \(y=3-x\) about the \(x\)-axis.
Solution We begin by graphing the two functions. See Figure 24(a). The \(x\)-coordinates of the points of intersection of the graphs satisfy the equation \begin{eqnarray*} \dfrac{2}{x} &=&3-x \\[3pt] x^{2}-3x+2 &=&0 \\[3pt] ( x-1) ( x-2) &=&0 \end{eqnarray*}
So, the region to be revolved lies between \(x=1\) and \(x=2\). Notice that the graph of \(y=3-x\) lies above the graph of \(y=\dfrac{2}{x}\) on the interval \(\left[ 1,\,2\right]\).
As illustrated in Figure 24(b), if we partition the \(x\)-axis, the volume \(V_{i}\) of a typical washer is \begin{equation*} V_{i}=\pi \left[ \left( \hbox{Outer radius}\right) ^{2}-\left( \hbox{Inner radius}\right) ^{2}\right] \Delta x=\pi \left[ (3-u_{i})^{2}-\left( \frac{2}{u_{i}}\right) ^{2}\right] \Delta x \end{equation*}
The volume \(V\) of the solid of revolution is \begin{eqnarray*} V&=&\pi \displaystyle \int_{1}^{2}\left[ (3-x)^{2}-\left( \dfrac{2}{x}\right) ^{2}\right]~{\it dx}=\pi \displaystyle \int_{1}^{2}\left( 9-6x+x^{2}-\dfrac{4}{x^{2}}\right) ~{\it dx}\\[4pt] &=&\pi \left[9x-3x^{2}+\dfrac{x^{3}}{3}+\dfrac{4}{x}\right] _{1}^{2}=\dfrac{\pi}{3}\hbox{ cubic units} \end{eqnarray*}
NOW WORK
4 Use the Washer Method to Find the Volume of a Solid Formed by Revolving a Region About the \(y\)-AxisPrinted Page 420
420
If we use the washer method and the region bounded by the graphs of two functions is revolved about the \(y\)-axis, we partition the \(y\)-axis, and the thickness of a typical washer will be \(\Delta y\).
EXAMPLE 5Using the Washer Method: Revolving About the \(y\)-Axis
Find the volume \(V\) of the solid of revolution generated by revolving the region enclosed by the graphs of \(y=2x\) and \(y=x^{2}\) about the \(y\)-axis.
Solution We begin by graphing the two functions. See Figure 25(a). The \(x\)-coordinates of the points of intersection of the graphs satisfy the equation \begin{eqnarray*} 2x &=&x^{2} \\[2pt] x^{2}-2x &=&0 \\[2pt] x(x-2) &=&0 \\[2pt] x &=&0\quad \hbox{or}\quad x=2 \end{eqnarray*}
The points of intersection are \((0,0)\) and \((2,4)\). The limits of integration are from \(y=0\) to \(y=4\).
Since the solid is formed by revolving the region about the \(y\)-axis from \(y=0\) to \(y=4\), we write \(y=2x\) as \(x=\dfrac{y}{2}\) and \(y=x^{2}\) as \(x=\sqrt{y}\). The outer radius is \(\sqrt{y}\) and the inner radius is \(\dfrac{y}{2}\).
As Figure 25(b) illustrates, if we partition the \(y\)-axis, the volume \(V_{i}\) of a typical washer is \begin{equation*} V_{i}=\pi \left[ \left( \hbox{Outer radius}\right) ^{2}-\left( \hbox{Inner radius}\right) ^{2}\right] \Delta y=\pi \left[ ( \sqrt{v_{i}}) ^{2}-\left( \frac{v_{i}}{2}\right) ^{2}\right] \Delta y \end{equation*}
The volume \(V\) of the solid of revolution shown in Figure 25(c) is \begin{eqnarray*} V&=&\pi \displaystyle \int_{0}^{4}\left[ ( \sqrt{y}) ^{2}-\left( \frac{y}{2}\right) ^{2}\right] {\it dy}=\pi \displaystyle \int_{0}^{4}\left( y-\frac{y^{2}}{4}\right){\it dy}\\[4pt] &=&\pi \left[ \frac{y^{2}}{2}-\frac{y^{3}}{12}\right] _{0}^{4}=\frac{8\pi }{3}\hbox{ cubic units} \end{eqnarray*}
NOW WORK
5 Find the Volume of a Solid Formed by Revolving a Region About a Line Parallel to a Coordinate AxisPrinted Page 421
421
Earlier we stated that a solid of revolution can be generated by revolving a region about any line. Now we investigate how to find the volume of a solid formed by revolving a region about a line parallel to either the \(x\)-axis or the \(y\)-axis.
EXAMPLE 6Using the Washer Method: Revolving About a Horizontal Line
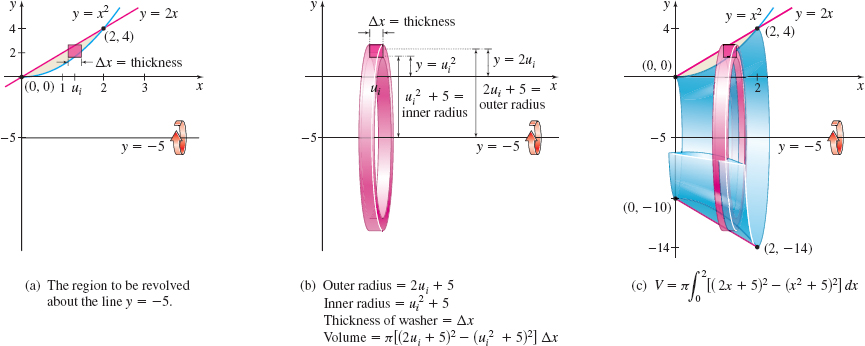
Find the volume \(V\) of the solid of revolution generated by revolving the region bounded by the graphs of \(y=2x\) and \(y=x^{2}\) about the line \(y=-5\).
Solution The region to be revolved is the same as in Example 5, but it is now being revolved about the line \(y=-5\). Figure 26 illustrates the region, a typical washer, and the solid of revolution.
Look at Figure 26(b). The outer radius of the washer is \(2u_i+5\) and the inner radius is \(u_i^{2}+5\). Partitioning the \(x\)-axis, the volume \(V_{i}\) of a typical washer is \[ V_{i}=\pi \Big[ ( 2u_{i}+5) ^{2}-\big( u_{i}^{2}+5\big) ^{2}\Big] \Delta x \]
The volume \(V\) of the solid of revolution as shown in Figure 26(c) is \begin{eqnarray*} V&=&\pi \displaystyle \int_{0}^{2}\Big[ ( 2x+5) ^{2}-( x^{2}+5) ^{2}\Big]\, {\it dx}=\pi \displaystyle \int_{0}^{2}( -x^{4}-6x^{2}+20x)\, {\it dx}\\[4pt] &=&\pi \left[ -\dfrac{x^{5}}{5}-2x^{3}+10x^{2}\right] _{0}^{2}=\dfrac{88}{5}\pi \hbox{ cubic units} \end{eqnarray*}
NOW WORK
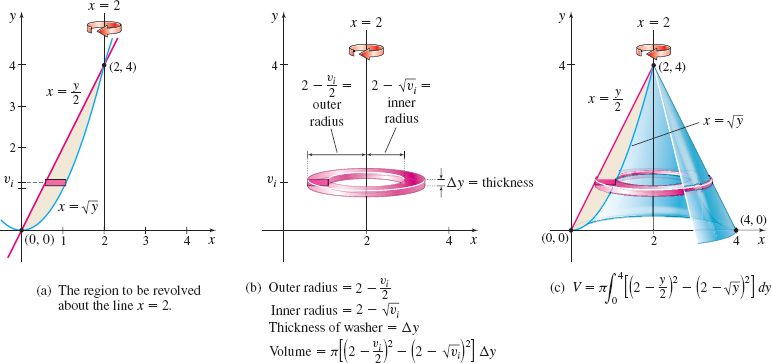
EXAMPLE 7Using the Washer Method: Revolving About a Vertical Line
Find the volume of the solid of revolution generated by revolving the region bounded by the graphs of \(y=2x\) and \(y=x^{2}\) about the line \(x=2\).
Solution This example is similar to Example 5 except that the region is revolved about the line \(x=2\). Figure 27 shows the graph of the region, a typical washer, and the solid of revolution.
422
Since the region is revolved about the vertical line \(x=2\), we express \(y=2x\) and \(y=x^2\) as \(x=\dfrac{y}{2}\) and \(x=\sqrt{y}\). The outer radius is \(2-\dfrac{y}{2}\) and the inner radius is \(2-\sqrt{y}\). The volume \(V\) of the solid of revolution is \begin{eqnarray*} V &=&\pi \displaystyle \int_{0}^{4}\left[ \left( 2-\dfrac{y}{2}\right) ^{2}-( 2- \sqrt{y}) ^{2}\right] ~{\it dy}\\[4pt] &=&\pi \displaystyle \int_{0}^{4}\left[ \left( 4-2y+\dfrac{ y^{2}}{4}\right) -( 4-4\sqrt{y}+y) \right] ~{\it dy} \\[4pt] &=&\pi \displaystyle \int_{0}^{4}\left( \dfrac{y^{2}}{4}-3y+4\sqrt{y}\right) ~{\it dy}=\pi \left[ \dfrac{y^{3}}{12}-\dfrac{3y^{2}}{2}+\dfrac{8y^{3/2}}{3}\right] _{0}^{4}=\dfrac{8}{3}\pi \hbox{ cubic units} \end{eqnarray*}