8.8 Power SeriesPrinted Page 600
600
In this section, we study series with variable terms, called power series. Just as a polynomial is the sum of a finite number of monomials, a power series is the sum of an infinite number of monomials.
DEFINITION Power Series
If \(x\) is a variable, then a series of the form \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \sum\limits_{k\,=\,0}^{\infty}a_{k}x^{k}=a_{0}+\sum\limits_{k=1}^{\infty}a_{k}x^{k}=a_{0}+a_{1}x+a_{2}x^{2}+\cdots}} \]
where the coefficients \(a_{0}, a_{1}, a_{2},\ldots\) are constants, is called a power series in \({\bf{x}}\) or a power series centered at \({\bf 0}\).
A series of the form \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \sum\limits_{k\,=\,0}^{\infty}a_{k}(x-c)^{k}=a_{0}+\sum\limits_{k=1}^{\infty }a_{k}(x-c)^{k}=a_{0}+a_{1}(x-c)+a_{2}(x-c)^{2}+\cdots }} \]
where \(c\) is a constant, is called a power series in \({\bf {(x-c)}}\) or a power series centered at \({\bf c}\).
If \(x=0\) in a power series \(\sum\limits_{k\,=\,0}^{\infty }a_{k}x^{k}\), then the power series equals \(a_{0}\). Also notice that the index \(k\) of a power series starts at \(0\).
IN WORDS
A power series \(\sum\limits_{k\,=\,0}^{\infty}{a}_{k}{\,x}^{k}\) is a sum of an infinite number of monomials.
1 Determine Whether a Power Series ConvergesPrinted Page 600
For a particular value of \(x\), a power series in \(x\) reduces to a series of real numbers like the series studied so far. For example, \(\sum\limits_{k=1}^{\infty }\dfrac{x^{k}}{k}\) is a power series in \(x\). The series converges (to \(0\)) if \(x=0\). If \(x=1\), it becomes the harmonic series \(\sum\limits_{k=1}^{\infty }\dfrac{1}{k}\), which is divergent. If \(x=-1\), it becomes the alternating harmonic series \(\sum\limits_{k=1}^{ \infty }(-1) ^{k}\dfrac{1}{k}\), which is convergent. To find all numbers \(x\) for which a power series in \(x\) is convergent, the Ratio Test (p. 591) or the Root Test (p. 593) are usually used since, in a power series, \(x\) is raised to a power.
EXAMPLE 1Determining Whether a Power Series Converges
Find all numbers \(x\) for which each power series in \(x\) converges.
- (a) \(\sum\limits_{k\,=\,0}^{\infty }\dfrac{x^{k}}{k!}=1+x+\dfrac{x^{2}}{2!}+\dfrac{x^{3}}{3!}+\cdots \)
- (b) \(\sum\limits_{k\,=\,0}^{\infty }\dfrac{kx^{k}}{4^{k}}=\dfrac{x}{4}+\dfrac{2x^{2}}{4^{2}}+\dfrac{3x^{3}}{4^{3}}+\cdots \)
- (c) \(\sum\limits_{k\,=\,0}^{\infty}k!x^{k}=1+x+2!x^{2}+3!x^{3}+\cdots \)
601
Solution (a) For the series \(\sum\limits_{k\,=\,0}^{\infty }\dfrac{x^{k}}{k!}\), we use the Ratio Test with \[ a_{n}=\frac{x^{n}}{n!}\qquad\hbox{and}\qquad a_{n+1}=\frac{x^{n+1}}{(n+1)!} \]
Then \[ \lim\limits_{n\rightarrow \infty }\left\vert \frac{a_{n+1}}{a_{n}}\right\vert =\lim\limits_{n\rightarrow \infty }\left\vert \frac{\dfrac{x^{n+1}}{(n+1) !}}{\dfrac{x^{n}}{n!}}\right\vert =\lim\limits_{n\rightarrow \infty } \frac{|x|^{n+1}\,n!}{(n+1)!\,|x|^{n}}=\vert x\vert \lim\limits_{n\rightarrow \infty }\frac{1}{n+1}=0 \]
Since the limit is less than \(1\) for every number \(x\), it follows from the Ratio Test that the power series \(\sum\limits_{k\,=\,0}^{\infty }\dfrac{x^{k}}{k!}\) is absolutely convergent for all real numbers.
NOTE
Since \(\sum\limits_{k\,=\,0}^{\infty} \dfrac{{ x}^{k}}{{k!}}\) converges absolutely for every number \(x\), the limit of the \(n\)th term equals \({0}\). That is, \(\lim\limits_{n\,\rightarrow \,\infty }\dfrac{{x}^{n}}{{n!}}={ 0}\) for every number \(x\).
(b) For \(\sum\limits_{k\,=\,0}^{\infty }\dfrac{kx^{k}}{4^{k}}\), we use the Ratio Test with \(a_{n}=\dfrac{nx^{n}}{4^{n}}\) and \(a_{n+1}=\dfrac{ (n+1)x^{n+1}}{4^{n+1}}\). Then \[ \begin{eqnarray*} \lim\limits_{n\,\rightarrow \,\infty }\left\vert \frac{a_{n+1}}{a_{n}} \right\vert &=& \lim\limits_{n\,\rightarrow \,\infty }\dfrac{\dfrac{ (n+1)\,\vert x\vert ^{n+1}}{4^{n+1}}}{\dfrac{n\,\,\vert x\vert ^{n}}{4^{n}}}=\lim\limits_{n\,\rightarrow \,\infty }\frac{ (n+1)\,|x|^{n+1}(4^{n})}{4^{n+1}\cdot n\,|x|^{n}} \\ &=& \vert x\vert \,\lim\limits_{n\,\rightarrow \,\infty }\frac{n+1}{4n}=\frac{|x|}{4} \end{eqnarray*} \]
By the Ratio Test, the series converges absolutely if \(\dfrac{|x|}{4} < 1\), or equivalently if \(\vert x\vert < 4\). It diverges if \(\dfrac{|x|}{4} \gt 1\) or equivalently if \(\vert x\vert >4\). The Ratio Test gives no information when \(\dfrac{|x|}{4}=1\), that is, when \(x=-4\) or \(x=4\). However, we can check these values directly by replacing \(x\) by \(4\) and \(-4\).
For \(x=4\), the series becomes \[ \sum_{k\,=\,0}^{\infty }\frac{k4^{k}}{4^{k}}=\sum_{k=1}^{\infty }k=1+2+\cdots \]
which diverges. For \(x=-4\), the series becomes \[ \sum_{k=0}^{\infty }\frac{k(-4)^{k}}{4^{k}}=\sum_{k=0}^{\infty }\frac{ (-1)^{k}k(4^{k})}{4^{k}}=\sum_{k=0}^{\infty }(-1)^{k}k=-1+2-3+\cdots \]
which also diverges. (Look at the sequence of partial sums.)
The series \(\sum\limits_{k\,=\,0}^{\infty }\dfrac{kx^{k}}{4^{k}}\) converges absolutely for \( -4< x< 4\) and diverges for \(\vert x\vert \geq 4\).
(c) For \(\sum\limits_{k\,=\,0}^{\infty }k!x^{k}\), we use the Ratio Test with \(a_{n}=n!\,x^{n}\) and \(a_{n+1}=(n+1)!\,x^{n+1}\). Then \[ \lim\limits_{n\,\rightarrow \,\infty }\left\vert \frac{a_{n+1}}{a_{n}} \right\vert =\lim\limits_{n\,\rightarrow \,\infty }\frac{(n+1)!\,\vert x\vert ^{n+1}}{n\dot{!}\,\vert x\vert ^{n}}=\vert x\vert\,\lim\limits_{n\,\rightarrow \,\infty } (n+1) =\left\{ \begin{array}{ll} 0 & \hbox{if} \, x=0 \\[4pt] \infty & \hbox{if} \, x\neq 0 \end{array} \right. \]
We conclude that the power series \(\sum\limits_{k\,=\,0}^{\infty }k!x^{k}\) converges only when \(x=0\). For any other number \(x\), the power series diverges.
NOW WORK
The next theorem gives more information about the numbers for which a power series converges or diverges.
602
THEOREM Convergence/Divergence of a Power Series
- (a) If the power series \(\sum\limits_{k\,=\,0}^{\infty }a_{k}x^{k}\) converges for a number \(x_{0}\neq 0\), then it converges absolutely for all numbers \(x\) for which \(\vert x\vert < \vert x_{0}\vert\).
- (b) If the power series \(\sum\limits_{k\,=\,0}^{\infty }a_{k}x^{k}\) diverges for a number \(x_{1}\), then it diverges for all numbers \(x\) for which \(\vert x\vert >\vert x_{1}\vert\).
RECALL
If a series \(\sum\limits_{k\,=\,0}^{\infty }{a}_{k}\) converges, then \(\lim\limits_{n\,\rightarrow \,\infty }a_{n}= 0\).
Proof
Part (a) Assume that \(\sum\limits_{k\,=\,0}^{\infty }a_{k}x_{0}^{k}\) converges. Then \[ \lim\limits_{n\rightarrow \infty }\left( a_{n}x_{0}^{n}\right) =0 \]
Using the definition of the limit of a sequence and choosing \(\varepsilon =1\) , there is a positive integer \(N\) for which \(\vert a_{n}x_{0}^{n} \vert < 1\) for all \(n > N\). Now for any number \(x\) for which \(\vert x\vert < |x_{0}|\), we have 
The series \(\sum\limits_{k\,=\,0}^{\infty }\left\vert \dfrac{x}{x_{0}} \right\vert ^{k}\) is a convergent geometric series since \(r=\left\vert \dfrac{x}{x_{0}}\right\vert < 1 (\vert x\vert < \vert x_{0}\vert)\). Therefore, by the Comparison Test for Convergence, the series \(\sum\limits_{k\,=\,0}^{\infty }\left\vert a_{k}x^{k}\right\vert\) converges, and so the power series \(\sum\limits_{k\,=\,0}^{\infty }a_{k}x^{k}\) converges absolutely for all numbers \(x\) such that \(\vert x\vert ≤ \vert x_{0}\vert\).
Part (b) Suppose the series converges for some number \(x\), \( \vert x\vert >|x_{1}|\). Then it must converge for \(x_{1}\) [by Part (a)], which contradicts the hypothesis of the theorem. Therefore, the series diverges for all \(x\) such that \(\vert x\vert >|x_{1}|\).
The next result is a consequence of the previous theorem. It states that every power series belongs to one of three categories.
THEOREM
For a power series \(\sum\limits_{k\,=\,0}^{\infty}a_{k} (x-c)^{k}\), exactly one of the following is true:
- The series converges only if \(x=c\).
- The series converges absolutely for all \(x\).
- There is a positive number \(R\) for which the series converges absolutely for all \(x\), \(\vert x-c\vert < R\), and diverges for all \(x,\) \(\vert x-c\vert >R\). The behavior of the series at \(\vert x-c\vert =R\) must be determined separately.
In the theorem, the number \(R\) is called the radius of convergence. If the series converges only for \(x=c\), then \(R=0;\) if the series converges absolutely for all \(x\), then \(R=\infty\). If the series converges absolutely for \(\vert x-c\vert < R\), \(0< R< \infty\), we call the set of all numbers \(x\) for which the power series converges the interval of convergence of the power series. Once the radius \(R\) of convergence is determined, we test the endpoints \(x=c-R\) and \(x=c+R\) to find the interval of convergence.
As Example 1 illustrates, the Ratio Test is a useful method for determining the radius of convergence of a power series. However, the test gives no information about convergence or divergence at the endpoints of the interval of convergence. At an endpoint, a power series may be absolutely convergent, conditionally convergent, or divergent.
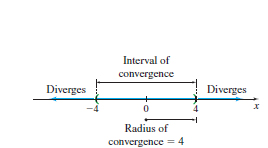
For example, the series \(\sum\limits_{k\,=\,0}^{\infty }\dfrac{kx^{k}}{4^{k}}\) in Example 1(b) converges absolutely for \(\vert x\vert < 4\) and diverges for \(\vert x\vert \geq 4\). So, the radius of convergence is \(R=4\), and the interval of convergence is the open interval \((-4,\,4)\), as shown in Figure 26.
2 Find the Interval of Convergence of a Power SeriesPrinted Page 603
603
EXAMPLE 2Finding the Interval of Convergence of a Power Series
Find the radius of convergence and the interval of convergence of the power series \[ \sum\limits_{k\,=\,1}^{\infty }\dfrac{x^{2k}}{k} \]
Solution We use the Ratio Test with \(a_{n}=\dfrac{x^{2n}}{n}\) and \(a_{n+1}=\dfrac{x^{2(n+1)}}{n+1}\). Then \[ \lim\limits_{n\,\rightarrow \,\infty}\left\vert \dfrac{a_{n+1}}{a_{n}}\right\vert =\lim\limits_{n\,\rightarrow \,\infty}\left\vert \dfrac{\dfrac{x^{2(n+1)}}{n+1}}{\dfrac{x^{2n}}{n}}\right\vert =\lim\limits_{n\,\rightarrow \,\infty}\left\vert \dfrac{\,x^{2n+2}}{n+1}\cdot \dfrac{n}{x^{2n}}\right\vert =x^{2}\lim\limits_{n\,\rightarrow \, \infty }\dfrac{n\,}{n+1}=x^{2} \]
The series converges absolutely if \(x^{2}< 1\), or equivalently, if \(-1< x< 1\).
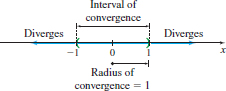
To determine the behavior at the endpoints, we investigate \(x=-1\) and \(x=1\). When \(x=1\) or \(x=-1\), \(\dfrac{x^{2k}}{k}=\dfrac{( x^{2}) ^{k}}{k}= \dfrac{1^{k}}{k}=\dfrac{1}{k}\), so the series reduces to the harmonic series \(\sum\limits_{k\,=\,1}^{\infty }\dfrac{1}{k}\), which diverges. Consequently, the radius of convergence is \(R=1\), and the interval of convergence is \(-1< x< 1\), as shown in Figure 27.
NOW WORK
EXAMPLE 3Finding the Interval of Convergence of a Power Series
Find the radius of convergence \(R\) and the interval of convergence of the power series \[ \sum\limits_{k\,=\,0}^{\infty }\dfrac{x^{k}}{(k+2) ^{2k}} \]
Solution We use the Root Test. Then \[ \lim\limits_{n\rightarrow \infty }\sqrt[n]{\left|\dfrac{x^{n}}{(n+2) ^{2n}}\right|}=\lim\limits_{n \rightarrow \infty }\dfrac{\vert x\vert }{(n+2) ^{2}} =\vert x\vert \lim\limits_{n\rightarrow \infty }\dfrac{1}{(n+2) ^{2}}=0 \]
The series converges absolutely for all \(x\). The radius of convergence is \( R=\infty\), and the interval of convergence is \((-\infty ,\infty)\).
NOW WORK
EXAMPLE 4Finding the Interval of Convergence of a Power Series
Find the radius of convergence \(R\) and the interval of convergence of the power series \[ \sum\limits_{k\,=\,0}^{\infty}(-1)^{k}\dfrac{(x-2)^{k}}{k+1} \]
Solution \(\sum\limits_{k\,=\,0}^{\infty }(-1)^{k}\dfrac{(x-2)^{k}}{k+1 }\) is a power series centered at \(2\). We use the Ratio Test with \( a_{n}=(-1)^{n}\dfrac{(x-2)^{n}}{n+1}\) and \(a_{n+1}=(-1)^{n+1} \dfrac{(x-2)^{n+1}}{n+2}\). Then \[ \begin{eqnarray*} \lim\limits_{n\rightarrow \infty }\left\vert \dfrac{a_{n+1}}{a_{n}}\right\vert &=& \lim\limits_{n\rightarrow \infty }\left\vert \frac{\dfrac{(-1)^{n+1}(x-2) ^{n+1}}{n+2}}{\dfrac{(-1)^{n}\,(x-2) ^{n}}{n+1}} \right\vert =\lim\limits_{n\rightarrow \infty }\left\vert \frac{(n+1)\,(x-2) }{n+2}\right\vert \nonumber \\ &=& \vert x-2\vert \,\lim\limits_{n\rightarrow \infty }\dfrac{n+1}{n+2}=\vert x-2\vert \end{eqnarray*} \]
604
The series converges absolutely if \(\vert x-2\vert < 1\), or equivalently if \(1 < x < 3\). The radius of convergence is \(R=1\). We check the endpoints \(x=1\) and \(x=3\) separately.
If \(x=1\), \[ \begin{eqnarray*} \sum\limits_{k\,=\,0}^{\infty }(-1)^{k}\dfrac{(x-2)^{k}}{k+1}&=&\sum \limits_{k\,=\,0}^{\infty }(-1)^{k}\dfrac{(-1) ^{k}}{k+1} =\sum\limits_{k\,=\,0}^{\infty }\dfrac{(-1) ^{2k}}{k+1} =\sum\limits_{k\,=\,0}^{\infty }\dfrac{1}{k+1}\nonumber \\ &=&1+\frac{1}{2}+\frac{1}{3}+\cdots + \frac{1}{n+1}+\cdots \end{eqnarray*} \]
which is the divergent harmonic series.
If \(x=3\), \[ \sum\limits_{k\,=\,0}^{\infty }(-1)^{k}\dfrac{(x-2)^{k}}{k+1}=\sum \limits_{k\,=\,0}^{\infty }(-1)^{k}\dfrac{1}{k+1}=1-\frac{1}{2}+\frac{1}{3}- \frac{1}{4}+\cdots +\frac{(-1)^{n}}{n+1}+\cdots \]
which is the convergent alternating harmonic series.
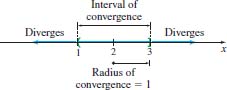
The series \(\sum\limits_{k\,=\,0}^{\infty }(-1)^{k}\dfrac{(x-2) ^{k} }{k+1}\) converges for \(1 < x\leq 3\), as shown in Figure 28.
NOW WORK
3 Define a Function Using a Power SeriesPrinted Page 604
A power series \(\sum\limits_{k\,=\,0}^{\infty }a_{k}x^{k}\) defines a function \(f\) whose domain is the interval of convergence of the power series. If \(I\) is the interval of convergence of \(\sum\limits_{k\,=\,0}^{\infty }a_{k}x^{k}\), the function \(f\) defined by the power series \(\sum\limits_{k\,=\,0}^{\infty }a_{k}x^{k}\) is \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ f(x)=a_{0}+a_{1}x+a_{2}x^{2}+\cdots +a_{n}x^{n}+\cdots }} \]
The domain of \(f\) is the interval of convergence \(I\).
If \(f\) is defined by the power series \(\sum\limits_{k\,=\,0}^{\infty}a_{k}x^{k}\), whose interval of convergence is \(I\), and if \(x_{0}\) is a number in \(I\), then \(f\) can be evaluated at \(x_{0}\) by finding the sum of the series \[ f(x_{0})=\sum\limits_{k\,=\,0}^{\infty }a_{k}x_{0}^{k}=a_{0}+a_{1}x_{0}+a_{2}x_{0}^{2}+\cdots +a_{n}x_{0}^{n}+\cdots \]
EXAMPLE 5Analyzing a Function Defined by a Power Series
A function \(f\) is defined by the power series \(f(x)=\sum\limits_{k\,=\,0}^{\infty }x^{k}\).
- (a) Find the domain of \(f\).
- (b) Evaluate \(f\left(\dfrac{1}{2}\right)\) and \(f\left(-\dfrac{1}{3}\right)\).
- (c) Find \(f\).
Solution (a) \(\sum\limits_{k\,=\,0}^{\infty }x^{k}\) is a power series centered at \(0\) with \(a_{k}=1\). Then \[ f(x) =1+x+x^{2}+x^{3}+x^{4}+ \cdots \]
The domain of \(f\) equals the interval of convergence of the power series. Since the series \(\sum\limits_{k\,=\,0}^{\infty }x^{k}\) is a geometric series, it converges for \(\vert x\vert < 1\). The radius of convergence is \(1\), and the interval of convergence is \((-1,1)\). The domain of \(f\) is the open interval \((-1,1) \).
605
(b) The numbers \(\dfrac{1}{2}\) and \(-\dfrac{1}{3}\) are in the interval \((-1,1)\), so they are in the domain of \(f\). Then \(f\left( \dfrac{1}{2}\right)\) is a geometric series with \(r=\dfrac{1}{2}\), \(a=1\), and \[ f\left(\dfrac{1}{2}\right) =1+\dfrac{1}{2}+\left(\dfrac{1}{2}\right) ^{2}+\left(\dfrac{1}{2}\right) ^{3}+\cdots \,= \frac{a}{1-r} = \dfrac{1}{1-\dfrac{1}{2}}=2 \]
Similarly, \[ f\left( -\dfrac{1}{3}\right) =1-\dfrac{1}{3}+\left( -\dfrac{1}{3}\right) ^{2}+\left( -\dfrac{1}{3}\right) ^{3}+\cdots \,=\dfrac{1}{1+\dfrac{1}{3}}=\dfrac{3}{4} \]
(c) Since \(f\) is defined by a geometric series, we can find \(f\) by summing the series. \[ \begin{eqnarray*} &&f(x) =\sum\limits_{k\,=\,0}^{\infty }x^{k} = 1 + x + x^{2} + \cdots + x^{n} + \cdots \underset{\underset{\color{#00ADEE}{a=1; r = x }}{\color{#00ADEE}{\uparrow}}}{=}\dfrac{1}{1-x}\quad -1 < x < 1\\ \end{eqnarray*} \]
In Example 5, the function \(f\) defined by the power series \( \sum\limits_{k\,=\,0}^{\infty }x^{k}\) was found to be \(f(x) =\dfrac{1 }{1-x}=\) \(\sum\limits_{k\,=\,0}^{\infty }x^{k}\), \(-1< x< 1\). In this case, we say that the function \(f\) is represented by the power series.
NOW WORK
EXAMPLE 6Representing a Function by a Power Series Centered at \(0\)
Represent each of the following functions by a power series centered at \(0\):
- (a) \(h(x) =\dfrac{1}{1-2x^{2}}\)
- (b) \(g(x) =\dfrac{1}{3+x}\)
- (c) \(F(x) =\dfrac{x^{2}}{1-x}\)
Solution We use the function \(f(x) = \dfrac{1}{1-x}\), \(-1< x < 1\), represented by the geometric series \( \sum\limits_{k\,=\,0}^{\infty }x^{k}\).
(a) In the geometric series for \(f(x) =\dfrac{1}{1-x} , \) we replace \(x\) by \(2x^{2}\). This series converges if \(\vert 2x^{2}\vert < 1\), or equivalently if \(-\dfrac{\sqrt{2}}{2} < x < \dfrac{\sqrt{2}}{2}\). Then on the open interval \(\left( -\dfrac{\sqrt{2}}{2},\,\dfrac{\sqrt{2}}{2}\right)\), the function \(h\,(x) =\dfrac{1}{ 1-2x^{2}}\) is represented by the power series \[ \begin{eqnarray*} h(x) &=& \dfrac{1}{1-2x^{2}}=1+(2x^{2}) + (2x^{2}) ^{2}+ (2x^{2})^{3}+ \cdots \\ &=& 1+2x^{2}+4x^{4}+8x^{6}+\cdots+2^{n}x^{2n} +\cdots=\sum\limits_{k\,=\,0}^{ \infty }(2x^{2}) ^{k}= \sum\limits_{k\,=\,0}^{\infty }2^{k}x^{2k} \end{eqnarray*} \]
(b) We begin by writing \[ g(x) =\dfrac{1}{3+x}=\dfrac{1}{3}\left(\dfrac{1}{1+\dfrac{x}{3}} \right) =\dfrac{1}{3}\left[ \dfrac{1}{1-\left( -\dfrac{x}{3}\right) }\right] \]
606
Now in the geometric series for \(f(x) =\dfrac{1}{1-x}\), replace \( x\) by \(-\dfrac{x}{3}\). This series converges if \(\left\vert -\dfrac{x}{3} \right\vert < 1\), or equivalently if \(-3< x < 3\). Then in the open interval \( (-3,3) \), \(g(x) =\dfrac{1}{3+x}\) is represented by the power series \[ \begin{eqnarray*} g\,(x) &=& \dfrac{1}{3+x}=\dfrac{1}{3}\left[ 1+\left( -\dfrac{x}{3} \right) +\left( -\dfrac{x}{3}\right) ^{2}+\left( -\dfrac{x}{3}\right) ^{3}+\cdots\right] =\dfrac{1}{3}\sum\limits_{k\,=0}^{\infty }(-1) ^{k}\left( \dfrac{x}{3}\right) ^{k}\nonumber \\ &=&\sum\limits_{k\,=0}^{\infty }\dfrac{ (-1) ^{k}x^{k}}{3^{k+1}} \end{eqnarray*} \]
(c) \(F(x) =\dfrac{x^{2}}{1-x}=x^{2}\left( \dfrac{1}{ 1-x}\right)\). Now for all numbers in the interval \((-1,\,1)\), \[ \dfrac{1}{1-x}=1+x+x^{2}+\cdots+x^{n}+\cdots \]
So for any number \(x\) in the interval of convergence, \(-1< x < 1\), we have \[ F(x) =x^{2}\left( 1+x+x^{2}+\cdots+x^{n}+\cdots\right) =x^{2}+x^{3}+x^{4}+\cdots+x^{n+2}+\cdots\,=\sum\limits_{k\,=2}^{\infty }x^{k} \]
NOTE
Notice that the power series for \(F\) begins at \(k=2\).
NOW WORK
4 Use Properties of Power SeriesPrinted Page 606
The function \(f\) represented by a power series has properties similar to those of a polynomial. We state three of these properties without proof.
THEOREM Properties of Power Series
Let \(\sum\limits_{k\,=0}^{\infty }a_{k}x^{k}\) be a power series in \( x\) having a nonzero radius of convergence \(R\). Define the function \(f\) as \[ f(x)=\sum\limits_{k\,=\,0}^{\infty}a_{k}x^{k}=a_{0}+a_{1}x+a_{2}x^{2}+\cdots +a_{n}x^{n}+\cdots \quad -R< x< R \]
- Continuity property: \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \lim\limits_{x\,\rightarrow \,x_{0}}\left( \sum\limits_{k\,=\,0}^{\infty }a_{k}x^{k}\right) =\sum\limits_{k\,=\,0}^{\infty }\left( \lim\limits_{x\,\rightarrow \,x_{0}}a_{k}x^{k}\right) = \sum\limits_{k\,=\,0}^{\infty }a_{k}x_{0}^{k} \quad -R< x_{0}< R }} \]
- Differentiation property: \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \dfrac{d}{dx}\left( \sum\limits_{k\,=\,0}^{\infty }a_{k}x^{k}\right) =\sum\limits_{k\,=\,0}^{\infty }\left( \dfrac{d}{dx} a_{k}x^{k}\right) =\sum\limits_{k\,=\,1}^{\infty }k a_{k}x^{k-1} }} \]
- Integration property: \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \int_{0}^{x}\left(\sum\limits_{k\,=\,0}^{\infty }a_{k}t^{k}\right) dt=\sum\limits_{k\,=\,0}^{\infty }\left( \int_{0}^{x}a_{k}t^{k}~dt\right) =\sum\limits_{k\,=\,0}^{\infty }\dfrac{ a_{k}x^{k+1}}{k+1}}} \]
The differentiation and integration properties of power series state that a power series can be differentiated and integrated term-by-term and that the resulting series represent the derivative and integral, respectively, of the function represented by the original power series. Moreover, it can be shown that the power series obtained by differentiating (or integrating) a power series whose radius of convergence is \(R\), converges and has the same radius of convergence \(R\) as the original power series. (See Problem 86.)
607
The differentiation and integration properties can be used to obtain new functions defined by a power series.
CAUTION
The theorem states that the radii of convergence of the three series \(\sum\limits_{k\,=\,0}^{\infty}a_{k}x^{k}\), \(\sum\limits_{k\,=\,1}^{\infty }ka_{k}x^{k-1}\), and \(\sum\limits_{k\,=\,0}^{\infty } \dfrac{a_{k}x^{k+1}}{k+1}\) are the same. This does not imply that the intervals of convergence are the same; the endpoints of the interval must be checked separately for each series. For example, the interval of convergence of \(\sum\limits_{k\,=\,0}^{\infty }\dfrac{x^{k}}{k}\) is \([-1,1)\), but the interval of convergence of its derivative \(\sum\limits_{k\,=\,1}^{\infty }x^{k-1}\) is \((-1,1)\).
EXAMPLE 7Using the Differentiation Property of Power Series
Use the differentiation property of power series to find the derivative of \[ f(x) =\dfrac{1}{1-x}=\sum\limits_{k\,=\,0}^{\infty }x^{k} \]
Solution The function \(f(x) =\dfrac{1}{1-x}\), defined on the open interval \((-1,\,1) \), is represented by the power series \[ f(x) =\frac{1}{1-x}=1+x+x^{2}+ \cdots +x^{n}+\cdots = \sum\limits_{k\,=\,0}^{\infty }x^{k} \]
Using the differentiation property, we find that \[ f^{\prime} (x) =\frac{1}{(1-x)^{2}}=1+2x+3x^{2}+\cdots +nx^{n-1}+\cdots =\sum\limits_{k\,=1}^{\infty }kx^{k-1} \]
whose radius of convergence is \(1\).
NOW WORK
EXAMPLE 8Finding the Power Series Representation for \(\ln \dfrac{1}{1-x}\)
- (a) Find the power series representation for \(\ln \dfrac{1}{1-x}\).
- (b) Find \(\ln 2\).
Solution (a) If \(y=\ln \dfrac{1}{1-x}\), then \(y^\prime = \dfrac{1}{1-x}\). That is, \(y^\prime\) is represented by the geometric series \( \sum\limits_{k\,=\,0}^{\infty }x^{k}\), which converges on the interval \( (-1,\,1)\). So, if we use the integration property of power series for \(y^\prime =\dfrac{1}{1-x}\), we obtain a series for \(y=\ln \dfrac{1}{ 1-x}\). \[ \begin{eqnarray*} y^\prime &=&\dfrac{1}{1-x}=1+x+x^{2}+\cdots +x^{n}+\cdots = \sum\limits_{k\,=\,0}^{\infty }x^{k} \\ \int_{0}^{x}\dfrac{1}{1-t}dt &=&\int_{0}^{x}( 1+t+t^{2}+\cdots +t^{n}+\cdots) ~dt \nonumber\\ \ln \dfrac{1}{1-x} &=&x+\dfrac{x^{2}}{2}+\dfrac{x^{3}}{3}+\cdots+\dfrac{ x^{n+1}}{n+1}+\cdots\, =\sum\limits_{k\,=\,0}^{\infty }\dfrac{x^{k+1}}{k+1} \end{eqnarray*} \]
The radius of convergence of this series is \(1\).
To find the interval of convergence, we investigate the endpoints. When \( x=1, \) \[ x+\dfrac{x^{2}}{2}+\dfrac{x^{3}}{3}+\cdots+\dfrac{x^{n+1}}{n+1}+\cdots\,=1+ \dfrac{1}{2}+\dfrac{1}{3}+\cdots\, \]
the harmonic series, which diverges. When \(x=-1\), \[ x+\dfrac{x^{2}}{2}+\dfrac{x^{3}}{3}+\cdots+\dfrac{x^{n+1}}{n+1}+\cdots\,=-1+ \dfrac{1}{2}-\dfrac{1}{3}+\cdots+(-1) ^{n+1}\dfrac{1}{n+1}+\cdots \]
an alternating harmonic series, which converges. The interval of convergence of the power series \(\sum\limits_{k\,=\,1}^{\infty }\dfrac{x^{k}}{k}\) is \( [-1,\,1) \). So, \[ \begin{equation*} \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{\ln \dfrac{1}{1-x}=x+\dfrac{x^{2}}{2}+\dfrac{x^{3}}{3} +\cdots\,=\sum\limits_{k\,=\,0}^{\infty }\dfrac{x^{k+1}}{k+1}\qquad -1\leq x<1}} \tag{1} \end{equation*} \]
608
(b) To find \(\ln 2\), notice that when \(x=-1\), we have \(\ln \dfrac{1}{1-x} =\ln \dfrac{1}{2}=- \ln 2\). In (1) let \(x=-1\). Then \[ \begin{eqnarray*} -\ln 2 &=&-1+\dfrac{1}{2}-\dfrac{1}{3}+\cdots \nonumber \\ \ln 2 &=&1-\dfrac{1}{2}+\dfrac{1}{3}\,\cdots \end{eqnarray*} \]
The sum of the alternating harmonic series is \(\ln 2\).
NOW WORK
EXAMPLE 9Finding the Power Series Representation for \(\tan^{-1} {\bf x}\)
Show that the power series representation for \(\tan ^{-1}x\) is \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \tan ^{-1}x=x-\dfrac{x^{3}}{3}+\dfrac{x^{5}}{5}-\dfrac{ x^{7}}{7}+\cdots +(-1)^{n}\dfrac{x^{2n+1}}{2n+1}+\cdots =\sum\limits_{k\,=\,0}^{\infty }\dfrac{(-1) ^{k}x^{2k+1}}{2k+1} }} \]
ORIGINS
The power series representation for \(\tan^{-1}x\) is called Gregory’s series (or Gregory–Leibniz series or Madhava–Gregory series). James Gregory (1638–1675) was a Scottish mathematician. His mother, Janet Anderson, was his teacher and taught him geometry. Gregory, like many other mathematicians of his time, was searching for a good way to approximate \(\pi\), a result of which was Gregory’s series. Gregory was also a major contributor to the theory of optics, and he is credited with inventing the reflective telescope.

Find the radius of convergence and the interval of convergence.
Solution If \(y=\tan ^{-1}x\), then \(y^\prime =\dfrac{1}{1+x^{2}}\), which is the sum of the geometric series \(\sum\limits_{k\,=\,0}^{\infty}(-1) ^{k}x^{2k}\). That is, \[ \dfrac{1}{1+x^{2}}=\sum\limits_{k\,=\,0}^{\infty }(-1) ^{k}x^{2k}=1-x^{2}+x^{4}-x^{6}+\cdots\, \]
This series converges when \(\vert x^{2}\vert < 1\), or equivalently for \(-1 < x < 1\). We use the integration property of power series to integrate \( y^\prime =\dfrac{1}{1+x^{2}}\) and obtain a series for \(y=\tan ^{-1}x\). \[ \begin{eqnarray*} \int_{0}^{x}\frac{dt}{1+t^{2}} &=&\int_{0}^{x}(1-t^{2}+t^{4}-\cdots)\, dt \nonumber \\ \tan ^{-1}x &=& x-\frac{x^{3}}{3}+\frac{x^{5}}{5}-\frac{x^{7}}{7}+\cdots +(-1)^{n}\frac{x^{2n+1}}{2n+1}+\cdots = \sum\limits_{k\,=\,0}^{\infty }(-1) ^{k}\dfrac{x^{2k+1}}{2k+1} \end{eqnarray*} \]
The radius of convergence is \(1\). To find the interval of convergence, we check \(x=-1\) and \(x=1\). For \(x=-1\), \[ -1+\frac{1}{3}-\frac{1}{5}+\frac{1}{7}-\cdots \]
For \(x=1\), we get \[ 1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\cdots \]
Both of these series satisfy the two conditions of the Alternating Series Test, and so each one converges. The interval of convergence is the closed interval \([-1,\,1] \).
609
Since \(\tan ^{-1}1=\dfrac{\pi }{4}\), we can use Gregory’s series to approximate \(\pi \). Then \[ \dfrac{\pi }{4}=\sum\limits_{k\,=\,0}^{\infty }(-1) ^{k}\dfrac{1^{2k+1}}{2k+1}= \sum\limits_{k\,=\,0}^{\infty }\dfrac{(-1) ^{k}}{2k+1}=1-\dfrac{1}{3}+\dfrac{1}{5}-\cdots \]
While we now have an approximation for \(\pi\), unfortunately the series converges very slowly, requiring many terms to get close to \(\pi\). See Problem 82.