9.3 Surface Area of a Solid of RevolutionPrinted Page 656
656
OBJECTIVES
When you finish this section, you should be able to:
In Chapter 6, we used a definite integral to find the volume of a solid of revolution. To obtain the solid of revolution, we revolved a region around an axis. Here, we are interested in finding the surface area of the solid of revolution. To obtain the surface, we revolve a smooth curve about an axis.
NOTE
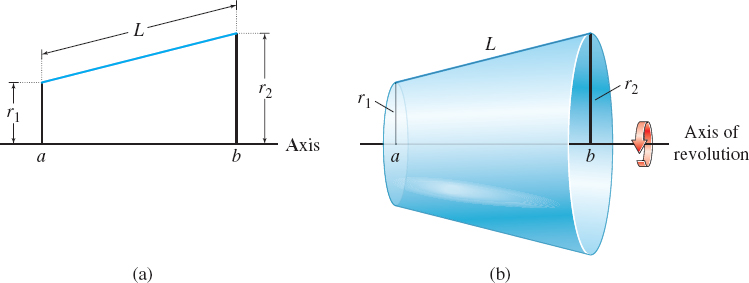
A frustum is a portion of a solid of revolution that lies between two parallel planes.
Consider a line segment of length \(L\) that lies above the \(x\)-axis. See Figure 19(a). If the region bounded by the line segment and the \(x\)-axis from \(a\) to \(b\) is revolved about an axis, the resulting solid of revolution is a frustum. The frustum of a right circular cone has slant height \(L\) and base radii \(r_{1}\) and \(r_{2}.\) See Figure 19(b).
The surface area \(S\) of the frustum is \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ S=2\pi \left( \dfrac{r_{1}+r_{2}}{2}\right)\, L }} \]
That is, the surface area \(S\) equals the product of \(2\pi ,\) the average radius of the frustum, and the slant height of the frustum. This equation forms the basis for the formula for the surface area of a solid of revolution.
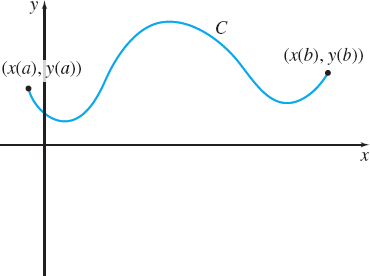
Suppose \(C\) is a smooth curve represented by the parametric equations \[ \begin{equation*} x=x (t)\qquad y=y(t)\quad a\leq t\leq b \end{equation*} \]
where \(y=y(t)\geq 0\) on the closed interval \([a,b],\) as shown in Figure 20. Revolving \(C\) about the \(x\)-axis generates a solid of revolution with surface area \(S\). To find \(S,\) we partition the interval \([ a,b] \) into \(n\) subintervals: \[ \begin{equation*} \lbrack a ,t_{1}], [t_{1},t_{2}], \ldots , [t_{i-1},t_{i}], \ldots , [t_{n-1},b] \end{equation*} \]
each of length \(\Delta t=\dfrac{b-a}{n}\). Corresponding to each number \( a, t_{1}, t_{2}, \ldots , t_{i-1}, t_{i}, \ldots , t_{n-1}, b\), there is a point \(P_{0}, P_{1}, \ldots , P_{i-1}, P_{i}, \ldots , P_{n-1}, P_{n}\) on the curve \(C\). We join each point \(P_{i-1}\) to the next point \(P_{i}\) with a line segment and focus on the line segment joining the points \(P_{i-1}\) and \(P_{i}\). See Figure 21(a). When this line segment of length \( d(P_{i-1},P_{i})\) is revolved about the \(x\)-axis, it generates a frustum of a right circular cone whose surface area \(S_{i}\) is \[ \begin{equation*} S_{i}=2\pi \left[ \frac{y(t_{i-1})+y(t_{i})}{2}\right] \, \left[d\,(P_{i-1},P_{i})\right] \tag{1} \end{equation*} \]
657
See Figure 21(b).
We follow the same reasoning used for finding the arc length of a smooth curve, (Section 9.2). Using the distance formula, the length of the \(i\)th line segment is \[ \begin{equation*} d(P_{i-1},P_{i})= \sqrt{[ x(t_{i}) -x(t_{i-1}) ] ^{2}+[ y(t_{i}) -y(t_{i-1}) ] ^{2}} \end{equation*} \]
Now we apply the Mean Value Theorem to \(x(t) \) and \(y(t) \). There are numbers \(u_{i}\) and \(v_{i}\) in each open interval \( ( t_{i-1},t_{i}) \) for which \[ \begin{equation*} x(t_{i}) -x ( t_{i-1} ) =\left[ \dfrac{dx}{dt} (u_{i} ) \right] \, \Delta t\qquad\hbox{and}\qquad y(t_{i}) -y ( t_{i-1} ) =\left[ \dfrac{dy}{dt} ( v_{i} ) \right] \, \Delta t \end{equation*} \]
So, \[ \begin{eqnarray*} d(P_{i-1},P_{i})&=& \sqrt{\left\{ \left[ \dfrac{dx}{dt}( u_{i}) \right] \, \Delta t\right\} ^{2}+ \left\{ \left[ \dfrac{dy}{dt}(v_{i}) \right] \, \Delta t\right\} ^{2}}\\[5pt] &=& \sqrt{\left[ \frac{dx}{dt}(u_{i})\right] ^{2}+ \left[ \frac{dy}{dt}(v_{i})\right] ^{2}}\,\Delta t \end{eqnarray*} \]
where \(u_{i}\) and \(v_{i}\) are numbers in the \(i\)th subinterval.
Now we replace \(d(P_{i-1},P_{i})\) in equation (1) with \(\sqrt{\left[ \dfrac{dx}{dt}(u_{i})\right] ^{2}+\left[ \dfrac{dy}{dt}(v_{i})\right] ^{2}}\,\Delta t\). Then the surface area generated by the sum of the line segments is \[ \begin{equation*} \sum_{i=1}^{n}S_{i}=\sum_{i=1}^{n}2\pi \left[ \frac{y(t_{i-1})+y(t_{i})}{2} \right] \, \sqrt{\left[ \frac{dx}{dt}(u_{i})\right] ^{2}+\left[ \frac{dy}{dt} (v_{i})\right] ^{2}}\,\Delta t \end{equation*} \]
These sums approximate the surface area generated by revolving \(C\) about the \(x\)-axis and lead to the following result.
THEOREM Surface Area of a Solid of Revolution
The surface area \(S\) of a solid of revolution generated by revolving the smooth curve \(C\) represented by \(x=x(t),\;y=y(t),\;a\leq t\leq b\), where \(y(t)\geq 0\), about the \(x\)-axis is \[ \begin{equation*} \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ S=2\pi \int_{a}^{b}y(t) \sqrt{\left( \dfrac{dx}{dt}\right) ^{2}+\left( \dfrac{dy}{dt}\right) ^{2}}\,dt }}\tag {2} \end{equation*} \]
1 Find the Surface Area of a Solid of Revolution Obtained from Parametric EquationsPrinted Page 659
658
EXAMPLE 1Finding the Surface Area of a Solid of Revolution Obtained from Parametric Equations
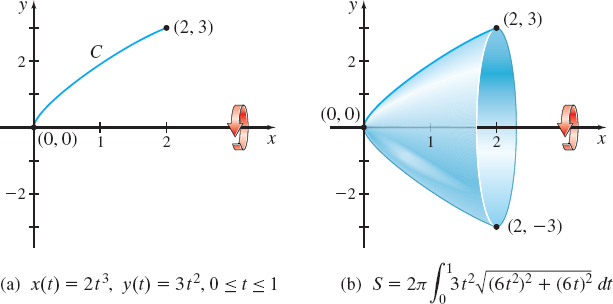
Find the surface area of the solid generated by revolving the smooth curve \( C \) represented by the parametric equations \(x(t) =2t^{3},\) \(y(t) =3t^{2},\) \(0\leq t\leq 1\), about the \(x\)-axis.
Solution We begin by graphing the smooth curve \(C\) and revolving it about the \(x\)-axis. See Figure 22.
We use formula (2) with \(\dfrac{dx}{dt}=\dfrac{d}{dt}\,\left( 2t^{3}\right) =6t^{2}\) and \( \dfrac{dy}{dt}=\dfrac{d}{dt}\,\left( 3t^{2}\right) =6t\). Then \begin{eqnarray*} S &=&2\pi \int_{a}^{b}\,y(t) \, \sqrt{\left( \dfrac{dx}{dt}\right) ^{2}+\left( \dfrac{ dy}{dt}\right) ^{2}}\,dt=2\pi \int_{0}^{1}\,3t^{2}\,\sqrt{( 6t^{2})^{2}+( 6t) ^{2}}\,dt\\[5pt] &=&2\pi \int_{0}^{1}\,3t^{2}\,\sqrt{36t^{4}+36t^{2}}\,dt =36\pi \int_{0}^{1}\,t^{3}\,\sqrt{t^{2}+1}\,dt=\frac{36\pi }{2}\int_{1}^{2}\,(u-1)\sqrt{u}\,du\\[-10pt] &&\hspace{10.9pc}\underset{\underset{{{\color{#00ADEE}{{\hbox{when \(t=0, u=1;\) when \(t=1, u=2\)}}}}}}{\color{#00ADEE}{{{\hbox{\(u=t^{2}+1;\)}}} {\color{#00ADEE}{\hbox{\(du=2t dt\)}}}} \,} }{\color{#00ADEE}{{{\uparrow }}}}\\[-3pt] &=&18\pi\,\left[ \dfrac{2}{5}u^{5/2}-\frac{2}{3}u^{3/2}\right]_{1}^{2}=\frac{24\pi }{5}\,(\sqrt{2}+1) \end{eqnarray*}
The surface area of the solid of revolution is \(\dfrac{24\pi }{5}(\sqrt{2} +1)\approx 36.405\) square units.
NOW WORK
To help remember the formula for the surface area of a solid of revolution, think of the integrand as the product of the slant height \(\sqrt{\left( \dfrac{dx}{dt}\right) ^{2}+\left( \dfrac{dy}{dt}\right) ^{2}}\) and the circumference \(2\pi y\) of the circle traced by a point \((x,y)\) on the corresponding sub-arc. Also keep in mind that the limits of integration are parameter values, not \(x\) values.
If the curve is revolved about the \(y\)-axis, we have a similar formula for the surface area of the solid of revolution.
THEOREM Surface Area of a Solid of Revolution
The surface area \(S\) of a solid of revolution generated by revolving the smooth curve \(C\) represented by \(x=x(t),\) \(y=y(t),\) \(a\leq t\leq b\), where \(x=x(t)\geq 0\), about the \(y\)-axis is \[\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ S=2\pi \int_{a}^{b} \, x(t) \sqrt{\left( \dfrac{dx}{dt}\right) ^{2}+\left( \dfrac{dy}{dt}\right) ^{2}}\,dt }} \]
2 Find the Surface Area of a Solid of Revolution Obtained from a Rectangular EquationPrinted Page 659
659
Let \(C\) be a smooth curve represented by a rectangular equation \( y=f(x), \) \(\ a\leq x\leq b\), where \(f(x)\geq 0\) on \([a,b]\). A set of parametric equations for this curve is \(x(t) =t\) and \(y(t) =f(t) \). Then \(\dfrac{dx}{dt}=1,\) \(dx=dt,\) and \(\ \dfrac{dy}{dt}= \dfrac{dy}{dx}\dfrac{dx}{dt}=\dfrac{dy}{dx}\cdot 1=f’ ( x) \). The surface area \(S\) of the solid of revolution obtained by revolving \(C,\) \(a\leq x\leq b \), about the \(x\)-axis is \(S=2\pi \int_{a}^{b}\,y(t) \sqrt{\left( \dfrac{dx}{dt}\right) ^{2}+\left( \dfrac{dy}{dt}\right) ^{2}}\,dt.\) So in terms of \(y=f( x) ,\) \(a\leq x\leq b,\) we have \[ \begin{equation*} \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ S=2\pi \int_{a}^{b}\,f( x) \sqrt{1+[ f’ ( x) ] ^{2}}\,dx }} \tag{3} \end{equation*} \]
EXAMPLE 2Finding the Surface Area of a Solid of Revolution Obtained from a Rectangular Equation
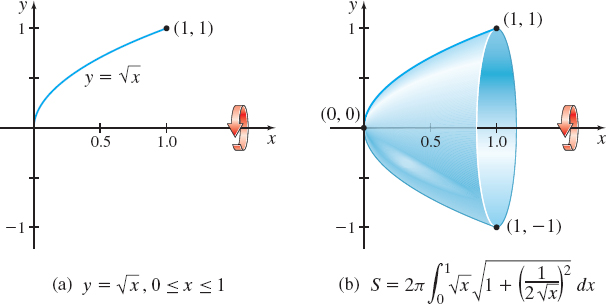
Find the surface area of the solid generated by revolving the curve represented by \(y= \sqrt{x},\) from \(x=0\) to \(x=1\), about the \(x\)-axis.
Solution We begin with the graph of \(y=\sqrt{x} ,\) \(0\leq x\leq 1,\) and revolve it about the \(x\)-axis, as shown in Figure 23.
We use formula (3) with \(f( x) = \sqrt{x}\) and \(f’ ( x) =\dfrac{1}{2 \sqrt{x}}.\) The surface area \(S\) we seek is

The surface area of the solid of revolution is \(\dfrac{\pi }{6}(5 \sqrt{5} -1)\approx 5.330\) square units.