1.3Concepts from Chemistry Explain the Properties of Biological Molecules
Concepts from Chemistry Explain the Properties of Biological Molecules
We have seen how a chemical insight into the hydrogen-
The formation of the DNA double helix as a key example
We will use these concepts to examine an archetypical biochemical process—
The double helix can form from its component strands

The discovery that DNA from natural sources exists in a double-
What forces cause the two strands of DNA to bind to each other? To analyze this binding reaction, we must consider several factors: the types of interactions and bonds in biochemical systems and the energetic favorability of the reaction. We must also consider the influence of the solution conditions—
Covalent and noncovalent bonds are important for the structure and stability of biological molecules
Atoms interact with one another through chemical bonds. These bonds include the covalent bonds that define the structure of molecules as well as a variety of noncovalent bonds that are of great importance to biochemistry.
Covalent bonds.
The strongest bonds are covalent bonds, such as the bonds that hold the atoms together within the individual bases shown in Section 1.2. A covalent bond is formed by the sharing of a pair of electrons between adjacent atoms. A typical carbon– C) covalent bond has a bond length of 1.54 Å and bond energy of 355 kJ mol−1 (85 kcal mol−1). Because covalent bonds are so strong, considerable energy must be expended to break them. More than one electron pair can be shared between two atoms to form a multiple covalent bond. For example, three of the bases in Figure 1.6 include carbon–
C) covalent bond has a bond length of 1.54 Å and bond energy of 355 kJ mol−1 (85 kcal mol−1). Because covalent bonds are so strong, considerable energy must be expended to break them. More than one electron pair can be shared between two atoms to form a multiple covalent bond. For example, three of the bases in Figure 1.6 include carbon– O) double bonds. These bonds are even stronger than C
O) double bonds. These bonds are even stronger than C C single bonds, with energies near 730 kJ mol−1 (175 kcal mol−1) and are somewhat shorter.
C single bonds, with energies near 730 kJ mol−1 (175 kcal mol−1) and are somewhat shorter.
7
For some molecules, more than one pattern of covalent bonding can be written. For example, adenine can be written in two nearly equivalent ways called resonance structures.
Distance and energy units
Interatomic distances and bond lengths are usually measured in angstrom (Å) units:
1 Å = 10−10 m = 10−8 cm = 0.1 nm
Several energy units are in common use. One joule (J) is the amount of energy required to move 1 meter against a force of 1 newton. A kilojoule (kJ) is 1000 joules. One calorie is the amount of energy required to raise the temperature of 1 gram of water 1 degree Celsius. A kilocalorie (kcal) is 1000 calories. One joule is equal to 0.239 cal.
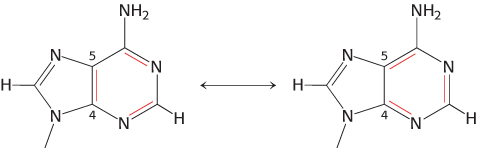
These adenine structures depict alternative arrangements of single and double bonds that are possible within the same structural framework. Resonance structures are shown connected by a double- C single bond (1.54 Å) and a C
C single bond (1.54 Å) and a C C double bond (1.34 Å). A molecule that can be written as several resonance structures of approximately equal energies has greater stability than does a molecule without multiple resonance structures.
C double bond (1.34 Å). A molecule that can be written as several resonance structures of approximately equal energies has greater stability than does a molecule without multiple resonance structures.
Noncovalent bonds.
Noncovalent bonds are weaker than covalent bonds but are crucial for biochemical processes such as the formation of a double helix. Four fundamental noncovalent bond types are ionic interactions, hydrogen bonds, van der Waals interactions, and hydrophobic interactions. They differ in geometry, strength, and specificity. Furthermore, these bonds are affected in vastly different ways by the presence of water. Let us consider the characteristics of each type:
1. Ionic Interactions. A charged group on one molecule can attract an oppositely charged group on the same or another molecule. The energy of an ionic interaction (sometimes called an electrostatic interaction) is given by the Coulomb energy:
E = kq1q2/Dr
where E is the energy, q1 and q2 are the charges on the two atoms (in units of the electronic charge), r is the distance between the two atoms (in angstroms), D is the dielectric constant (which decreases the strength of the Coulomb depending on the intervening solvent or medium), and k is a proportionality constant (k = 1389, for energies in units of kilojoules per mole, or 332 for energies in kilocalories per mole).
By convention, an attractive interaction has a negative energy. The ionic interaction between two ions bearing single opposite charges separated by 3 Å in water (which has a dielectric constant of 80) has an energy of −5.8 kJ mol−1 (−1.4 kcal mol−1). Note how important the dielectric constant of the medium is. For the same ions separated by 3 Å in a nonpolar solvent such as hexane (which has a dielectric constant of 2), the energy of this interaction is −232 kJ mol−1 (−55 kcal mol−1).
8
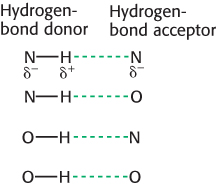
2. Hydrogen Bonds. These interactions are largely ionic interactions, with partial charges on nearby atoms attracting one another. Hydrogen bonds are responsible for specific base-
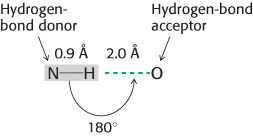
Hydrogen bonds are much weaker than covalent bonds. They have energies ranging from 4 to 20 kJ mol−1 (from 1 to 5 kcal mol−1). Hydrogen bonds are also somewhat longer than covalent bonds; their bond lengths (measured from the hydrogen atom) range from 1.5 Å to 2.6 Å; hence, a distance ranging from 2.4 Å to 3.5 Å separates the two nonhydrogen atoms in a hydrogen bond.

The strongest hydrogen bonds have a tendency to be approximately straight, such that the hydrogen-
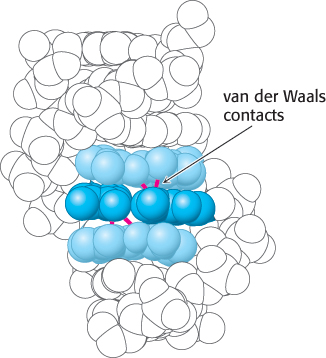
3. van der Waals Interactions. The basis of a van der Waals interaction is that the distribution of electronic charge around an atom fluctuates with time. At any instant, the charge distribution is not perfectly symmetric. This transient asymmetry in the electronic charge about an atom acts through ionic interactions to induce a complementary asymmetry in the electron distribution within its neighboring atoms. The atom and its neighbors then attract one another. This attraction increases as two atoms come closer to each other, until they are separated by the van der Waals contact distance (Figure 1.10). At distances shorter than the van der Waals contact distance, very strong repulsive forces become dominant because the outer electron clouds of the two atoms overlap.
Energies associated with van der Waals interactions are quite small; typical interactions contribute from 2 to 4 kJ mol−1 (from 0.5 to 1 kcal mol−1) per atom pair. When the surfaces of two large molecules come together, however, a large number of atoms are in van der Waals contact, and the net effect, summed over many atom pairs, can be substantial.
We will cover the fourth noncovalent interaction, the hydrophobic interaction, after we examine the characteristics of water; these characteristics are essential to understanding the hydrophobic interaction.
Properties of water.
Water is the solvent in which most biochemical reactions take place, and its properties are essential to the formation of macromolecular structures and the progress of chemical reactions. Two properties of water are especially relevant:
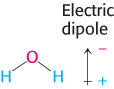
1. Water is a polar molecule. The water molecule is bent, not linear, and so the distribution of charge is asymmetric. The oxygen nucleus draws electrons away from the two hydrogen nuclei, which leaves the region around each hydrogen atom with a net positive charge. The water molecule is thus an electrically polar structure.
9
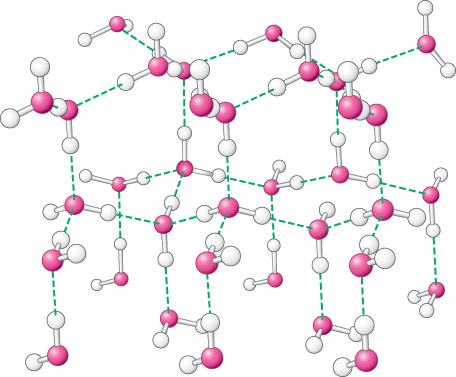
2. Water is highly cohesive. Water molecules interact strongly with one another through hydrogen bonds. These interactions are apparent in the structure of ice (Figure 1.11). Networks of hydrogen bonds hold the structure together; similar interactions link molecules in liquid water and account for many of the properties of water. In the liquid state, approximately one in four of the hydrogen bonds present in ice are broken. The polar nature of water is responsible for its high dielectric constant of 80. Molecules in aqueous solution interact with water molecules through the formation of hydrogen bonds and through ionic interactions. These interactions make water a versatile solvent, able to readily dissolve many species, especially polar and charged compounds that can participate in these interactions.
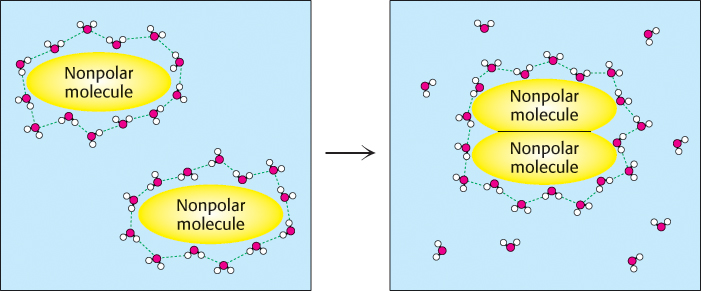
The hydrophobic effect.
A final fundamental interaction called the hydrophobic effect is a manifestation of the properties of water. Some molecules (termed nonpolar molecules) cannot participate in hydrogen bonding or ionic interactions. The interactions of nonpolar molecules with water molecules are not as favorable as are interactions between the water molecules themselves. The water molecules in contact with these nonpolar molecules form “cages” around them, becoming more well ordered than water molecules free in solution. However, when two such nonpolar molecules come together, some of the water molecules are released, allowing them to interact freely with bulk water (Figure 1.12). The release of water from such cages is favorable for reasons to be considered shortly. The result is that nonpolar molecules show an increased tendency to associate with one another in water compared with other, less polar and less self-
The double helix is an expression of the rules of chemistry
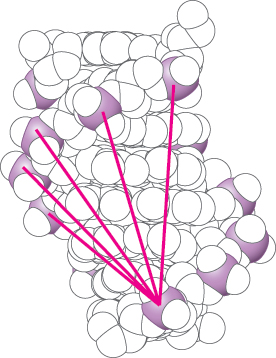
Let us now see how these four noncovalent interactions work together in driving the association of two strands of DNA to form a double helix. First, each phosphate group in a DNA strand carries a negative charge. These negatively charged groups interact unfavorably with one another over distances. Thus, unfavorable ionic interactions take place when two strands of DNA come together. These phosphate groups are far apart in the double helix with distances greater than 10 Å, but many such interactions take place (Figure 1.13). Thus, ionic interactions oppose the formation of the double helix. The strength of these repulsive ionic interactions is diminished by the high dielectric constant of water and the presence of ionic species such as Na+ or Mg2+ ions in solution. These positively charged species interact with the phosphate groups and partly neutralize their negative charges.
10
Second, as already noted, hydrogen bonds are important in determining the formation of specific base pairs in the double helix. However, in single-

When two single strands come together, these hydrogen bonds with water are broken and new hydrogen bonds between the bases are formed. Because the number of hydrogen bonds broken is the same as the number formed, these hydrogen bonds do not contribute substantially to driving the overall process of double-
Third, within a double helix, the base pairs are parallel and stacked nearly on top of one another. The typical separation between the planes of adjacent base pairs is 3.4 Å, and the distances between the most closely approaching atoms are approximately 3.6 Å. This separation distance corresponds nicely to the van der Waals contact distance (Figure 1.14). Bases tend to stack even in single-
Fourth, the hydrophobic effect also contributes to the favorability of base stacking. More-
The principles of double-
The laws of thermodynamics govern the behavior of biochemical systems
We can look at the formation of the double helix from a different perspective by examining the laws of thermodynamics. These laws are general principles that apply to all physical (and biological) processes. They are of great importance because they determine the conditions under which specific processes can or cannot take place. We will consider these laws from a general perspective first and then apply the principles that we have developed to the formation of the double helix.
11
The laws of thermodynamics distinguish between a system and its surroundings. A system refers to the matter within a defined region of space. The matter in the rest of the universe is called the surroundings. The First Law of Thermodynamics states that the total energy of a system and its surroundings is constant. In other words, the energy content of the universe is constant; energy can be neither created nor destroyed. Energy can take different forms, however. Heat, for example, is one form of energy. Heat is a manifestation of the kinetic energy associated with the random motion of molecules. Alternatively, energy can be present as potential energy —energy that will be released on the occurrence of some process. Consider, for example, a ball held at the top of a tower. The ball has considerable potential energy because, when it is released, the ball will develop kinetic energy associated with its motion as it falls. Within chemical systems, potential energy is related to the likelihood that atoms can react with one another. For instance, a mixture of gasoline and oxygen has a large potential energy because these molecules may react to form carbon dioxide and water and release energy as heat. The First Law requires that any energy released in the formation of chemical bonds must be used to break other bonds, released as heat or light, or stored in some other form.
Another important thermodynamic concept is that of entropy, a measure of the degree of randomness or disorder in a system. The Second Law of Thermodynamics states that the total entropy of a system plus that of its surroundings always increases. For example, the release of water from nonpolar surfaces responsible for the hydrophobic effect is favorable because water molecules free in solution are more disordered than they are when they are associated with nonpolar surfaces. At first glance, the Second Law appears to contradict much common experience, particularly about biological systems. Many biological processes, such as the generation of a leaf from carbon dioxide gas and other nutrients, clearly increase the level of order and hence decrease entropy. Entropy may be decreased locally in the formation of such ordered structures only if the entropy of other parts of the universe is increased by an equal or greater amount. The local decrease in entropy is often accomplished by a release of heat, which increases the entropy of the surroundings.
We can analyze this process in quantitative terms. First, consider the system. The entropy (S) of the system may change in the course of a chemical reaction by an amount ΔSsystem. If heat flows from the system to its surroundings, then the heat content, often referred to as the enthalpy (H), of the system will be reduced by an amount ΔHsystem. To apply the Second Law, we must determine the change in entropy of the surroundings. If heat flows from the system to the surroundings, then the entropy of the surroundings will increase. The precise change in the entropy of the surroundings depends on the temperature; the change in entropy is greater when heat is added to relatively cold surroundings than when heat is added to surroundings at high temperatures that are already in a high degree of disorder. To be even more specific, the change in the entropy of the surroundings will be proportional to the amount of heat transferred from the system and inversely proportional to the temperature (T) of the surroundings. In biological systems, T [in kelvins (K), absolute temperature] is usually assumed to be constant. Thus, a change in the entropy of the surroundings is given by
12
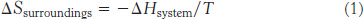
The total entropy change is given by the expression

Substituting equation 1 into equation 2 yields

Multiplying by −T gives

The function −TΔS has units of energy and is referred to as free energy or Gibbs free energy, after Josiah Willard Gibbs, who developed this function in 1878:

The free-
Recall that the Second Law of Thermodynamics states that, for a process to take place, the entropy of the universe must increase. Examination of equation 3 shows that the total entropy will increase if and only if
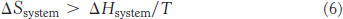
Rearranging gives TΔSsystem. ΔH or, in other words, entropy will increase if and only if

Thus, the free-
Heat is released in the formation of the double helix
Let us see how the principles of thermodynamics apply to the formation of the double helix (Figure 1.15). Suppose solutions containing each of the two single strands are mixed. Before the double helix forms, each of the single strands is free to translate and rotate in solution, whereas each matched pair of strands in the double helix must move together. Furthermore, the free single strands exist in more conformations than possible when bound together in a double helix. Thus, the formation of a double helix from two single strands appears to result in an increase in order for the system, that is, a decrease in the entropy of the system.

On the basis of this analysis, we expect that the double helix cannot form without violating the Second Law of Thermodynamics unless heat is released to increase the entropy of the surroundings. Experimentally, we can measure the heat released by allowing the solutions containing the two single strands to come together within a water bath, which here corresponds to the surroundings. We then determine how much heat must be absorbed by the water bath or released from it to maintain it at a constant temperature. This experiment reveals that a substantial amount of heat is released—
13
Acid–base reactions are central in many biochemical processes
Throughout our consideration of the formation of the double helix, we have dealt only with the noncovalent bonds that are formed or broken in this process. Many biochemical processes entail the formation and cleavage of covalent bonds. A particularly important class of reactions prominent in biochemistry is acid–base reactions.
In acid and base reactions, hydrogen ions are added to molecules or removed from them. Throughout the book, we will encounter many processes in which the addition or removal of hydrogen atoms is crucial, such as the metabolic processes by which carbohydrates are degraded to release energy for other uses. Thus, a thorough understanding of the basic principles of these reactions is essential.
A hydrogen ion, often written as H+, corresponds to a proton. In fact, hydrogen ions exist in solution bound to water molecules, thus forming what are known as hydronium ions, H3O+. For simplicity, we will continue to write H+, but we should keep in mind that H+ is shorthand for the actual species present.
The concentration of hydrogen ions in solution is expressed as the pH. Specifically, the pH of a solution is defined as
pH = −log[H+]
where [H+] is in units of molarity. Thus, pH 7.0 refers to a solution for which −log[H+] = 7.0, and so log[H+] = −7.0 and [H+] = 10log[H+] = 10−7.0 = 1.0 × 10−7 M.
The pH also indirectly expresses the concentration of hydroxide ions, [OH−], in solution. To see how, we must realize that water molecules can dissociate to form H+ and OH− ions in an equilibrium process.

The equilibrium constant (K) for the dissociation of water is defined as
K = [H+][OH−]/[H2O]
14
and has a value of K = 1.8 × 10−16. Note that an equilibrium constant does not formally have units. Nonetheless, the value of the equilibrium constant given assumes that particular units are used for concentration (sometimes referred to a standard states); in this case and in many others, units of molarity (M) are assumed.
The concentration of water, [H2O], in pure water is 55.5 M, and this concentration is constant under most conditions. Thus, we can define a new constant, KW:
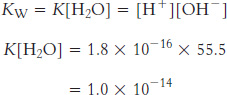
Because KW = [H+][OH−] = 1.0 × 10−14, we can calculate
[OH−] = 10−14/[H+] and [H+] = 10−14/[OH−]
With these relations in hand, we can easily calculate the concentration of hydroxide ions in an aqueous solution, given the pH. For example, at pH = 7.0, we know that [H+] = 10−7 M and so [OH−] = 10−14/10−7 = 10−7 M. In acidic solutions, the concentration of hydrogen ions is higher than 10−7 and, hence, the pH is below 7. For example, in 0.1 M HCl, [H+] = 10−1 M and so pH = 1.0 and [OH−] = 10−14/10−1 = 10−13 M.
Acid–base reactions can disrupt the double helix
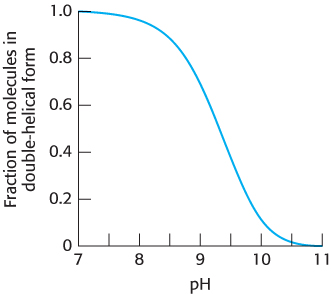
The reaction that we have been considering between two strands of DNA to form a double helix takes place readily at pH 7.0. Suppose that we take the solution containing the double-
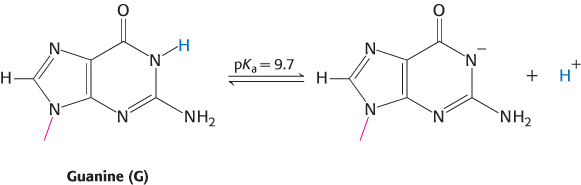
Proton dissociation for a substance HA (such as that bound to N-
Ka = [H+][A−]/[HA]
The susceptibility of a proton to removal by reaction with a base is often described by its pKa value:
pKa = −log(Ka)
15
When the pH is equal to the pKa, we have
pH = pKa
and so
−log[H+] = −log([H+][A−]/[HA])
and
[H+] = [H+][A−]/[HA]
Dividing by [H+] reveals that
1 = [A−]/[HA]
and so
[A−] = [HA]
Thus, when the pH equals the pKa, the concentration of the deprotonated form of the group or molecule is equal to the concentration of the protonated form; the deprotonation process is halfway to completion.
The pKa for the proton on N-
Buffers regulate pH in organisms and in the laboratory
These observations about DNA reveal that a significant change in pH can disrupt molecular structure. The same is true for many other biological macromolecules; changes in pH can protonate or deprotonate key groups, potentially disrupting structures and initiating harmful reactions. Thus, systems have evolved to mitigate changes in pH in biological systems. Solutions that resist such changes are called buffers. Specifically, when acid is added to an unbuffered aqueous solution, the pH drops in proportion to the amount of acid added. In contrast, when acid is added to a buffered solution, the pH drops more gradually. Buffers also mitigate the pH increase caused by the addition of base and changes in pH caused by dilution.
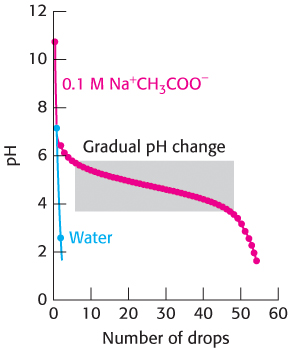
Compare the result of adding a 1 M solution of the strong acid HCl drop by drop to pure water with adding it to a solution containing 100 mM of the buffer sodium acetate (Na+CH3COO−; Figure 1.17). The process of gradually adding known amounts of reagent to a solution with which the reagent reacts while monitoring the results is called a titration. For pure water, the pH drops from 7 to close to 2 on the addition of the first few drops of acid. However, for the sodium acetate solution, the pH first falls rapidly from its initial value near 10, then changes more gradually until the pH reaches 3.5, and then falls more rapidly again. Why does the pH decrease so gradually in the middle of the titration? The answer is that, when hydrogen ions are added to this solution, they react with acetate ions to form acetic acid. This reaction consumes some of the added hydrogen ions so that the pH does not drop. Hydrogen ions continue reacting with acetate ions until essentially all of the acetate ion is converted into acetic acid. After this point, added protons remain free in solution and the pH begins to fall sharply again.
16
We can analyze the effect of the buffer in quantitative terms. The equilibrium constant for the deprotonation of an acid is
Ka = [H+][A−]/[HA]
Taking logarithms of both sides yields
log(Ka) = log([H+]) + log([A−]/[HA])
Recalling the definitions of pKa and pH and rearranging gives
pH = pKa + log([A−]/[HA])
This expression is referred to as the Henderson–Hasselbalch equation.
We can apply the equation to our titration of sodium acetate. The pKa of acetic acid is 4.75. We can calculate the ratio of the concentration of acetate ion to the concentration of acetic acid as a function of pH by using the Henderson–

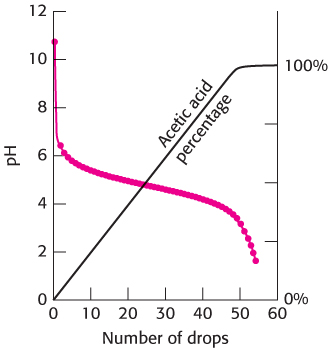
At pH 9, this ratio is 109−4.75 = 104.25 = 17,800; very little acetic acid has been formed. At pH 4.75 (when the pH equals the pKa), the ratio is 104.75−4.75 = 100 = 1. At pH 3, the ratio is 103−4.75 = 10−1.25 = 0.02; almost all of the acetate ion has been converted into acetic acid. We can follow the conversion of acetate ion into acetic acid over the entire titration (Figure 1.18). The graph shows that the region of relatively constant pH corresponds precisely to the region in which acetate ion is being protonated to form acetic acid.
From this discussion, we see that a buffer functions best close to the pKa value of its acid component. Physiological pH is typically about 7.4. An important buffer in biological systems is based on phosphoric acid (H3PO4). The acid can be deprotonated in three steps to form a phosphate ion.

At about pH 7.4, inorganic phosphate exists primarily as a nearly equal mixture of H2PO4− and HPO42−. Thus, phosphate solutions function as effective buffers near pH 7.4. The concentration of inorganic phosphate in blood is typically approximately 1 mM, providing a useful buffer against processes that produce either acid or base. We can examine this utility in quantitative terms with the use of the Henderson–
[HPO42−]/[H2PO4−] = 107.4−7.21 = 100.19 = 1.55
The total concentration of phosphate, [HPO42−] + [H2PO4−], is 1 mM, Thus,
[HPO42−] = (1.55/2.55) × 1 mM = 0.608 mM
and
[H2PO4−] = (1/2.55) × 1 mM = 0.392 mM
17
At pH 7.3,
[HPO42−]/[H2PO4−] = 107.3−7.21 = 100.09 = 1.23
and so
[HPO42−] = (1.23/2.23) = 0.552 mM
and
[H2PO4−] = (1/2.23) = 0.448 mM
Thus, (0.608 −0.552) = 0.056 mM HPO42− is converted into H2PO4−, consuming 0.056 mM = 5.6 × 10−5 M [H+]. Thus, the buffer increases the amount of acid required to produce a drop in pH from 7.4 to 7.3 by a factor of 5.6 × 10−5/1.0 × 10−8 = 5600 compared with pure water.