Most experiments that are performed to determine an enzyme characteristic require an enzyme preparation in a buffered solution. Even a few microliters of such a solution will contain millions of enzyme molecules. Much that we have learned about enzymes thus far has come from such experiments, called ensemble studies. A basic assumption of ensemble studies is that all of the enzyme molecules are the same or very similar. When we determine an enzymatic property such as the value of K_M in ensemble studies, that value is of necessity an average value of all of the enzyme molecules present. However, as discussed in Chapter 2, we now know that molecular heterogeneity, the ability of a molecule, over time, to assume several different structures that differ slightly in stability, is an inherent property of all large biomolecules. How can we tell if this molecular heterogeneity affects enzyme activity?

By way of example, consider a hypothetical situation. A Martian visits Earth to learn about higher education. The spacecraft hovers high above a university, and our Martian meticulously records how the student population moves about campus. Much information can be gathered from such studies: where students are likely to be at certain times on certain days, which buildings are used when and by how many. Now, suppose our visitor developed a high-magnification camera that could follow one student throughout the day. Such data would provide a much different perspective on college life: What does this student eat? To whom does she talk? How much time does she spend studying? This new in singulo method, examining one individual at a time, yields a great deal of new information but also illustrates a potential pitfall of studying individuals, be they students or enzymes: How can we be certain that the student or molecule is representative and not an outlier? This pitfall can be overcome by studying enough individuals to satisfy statistical analysis for validity.

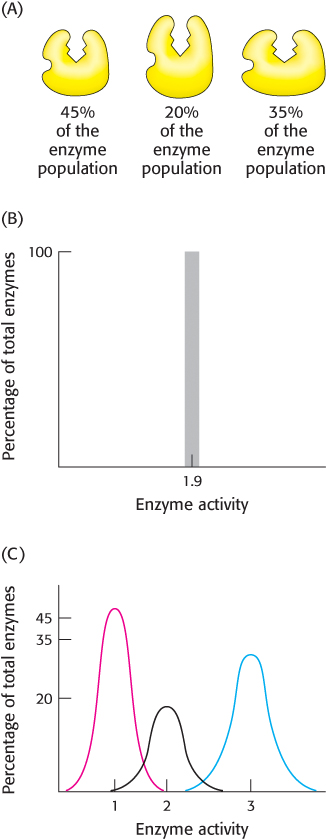
Let us leave our Martian to his observations, and consider a more biochemical situation. Figure 8.34A shows an enzyme that displays molecular heterogeneity, with three active forms that catalyze the same reaction but at different rates. These forms have slightly different stabilities, but thermal noise is sufficient to interconvert the forms. Each form is present as a fraction of the total enzyme population as indicated. If we were to perform an experiment to determine enzyme activity under a particular set of conditions with the use of ensemble methods, we would get a single value, which would represent the average of the heterogeneous assembly (Figure 8.34B). However, were we to perform a sufficient number of single-molecule experiments, we would discover that the enzyme has three different molecular forms with very different activities (Figure 8.34C). Moreover, these different forms would most likely correspond to important biochemical differences.

The development of powerful techniques—such as patch-clamp recording, single-molecule fluorescence, and optical tweezers—has enabled biochemists to look into the workings of individual molecules. We will examine single-molecule studies of membrane channels with the use of patch-clamp recording (Section 13.4), ATP-synthesizing complexes with the use of single-molecule fluorescence (Section 18.4) and molecular motors with the use of an optical trap (Section 34.2). We are now able to observe events at a molecular level that reveal rare or transient structures and fleeting events in a reaction sequence, as well as to measure mechanical forces affecting or generated by an enzyme. Single-molecule studies open a new vista on the function of enzymes in particular and on all large biomolecules in general.

243