5.2 Enzymes: The Reaction Catalysts of Biological Systems
Rare indeed is the organic chemical reaction that proceeds unaided at a rate sufficient to support living systems. Enzymes have extraordinary catalytic power, often far greater than that of synthetic or inorganic catalysts. They have a high degree of specificity for their substrates, they substantially accelerate chemical reactions, and they function in aqueous solutions under very mild conditions of temperature and pH. Few nonbiological catalysts have all these properties.
Enzymes are central to every cellular process. Acting in organized sequences, they catalyze the hundreds of stepwise reactions that degrade nutrient molecules, conserve and transform chemical energy, make biological macromolecules from simple precursors, and carry out the various processes of DNA and RNA metabolism.
In molecular biology, the study of enzymes has immense practical importance. In some diseases, especially hereditary genetic disorders related to DNA or RNA metabolism, there may be a deficiency or even a total absence of one or more enzymes. Other disease conditions may be caused by excessive activity of an enzyme. Many medicines act through interactions with enzymes. Furthermore, researchers can isolate and harness enzyme functions to suit their purposes in the laboratory. The set of methods collectively described as “biotechnology” (many of which are described in Chapter 7 and elsewhere throughout this book) is made possible by our understanding of the enzymes of DNA and RNA metabolism.
Enzymes Catalyze Specific Biological Reactions
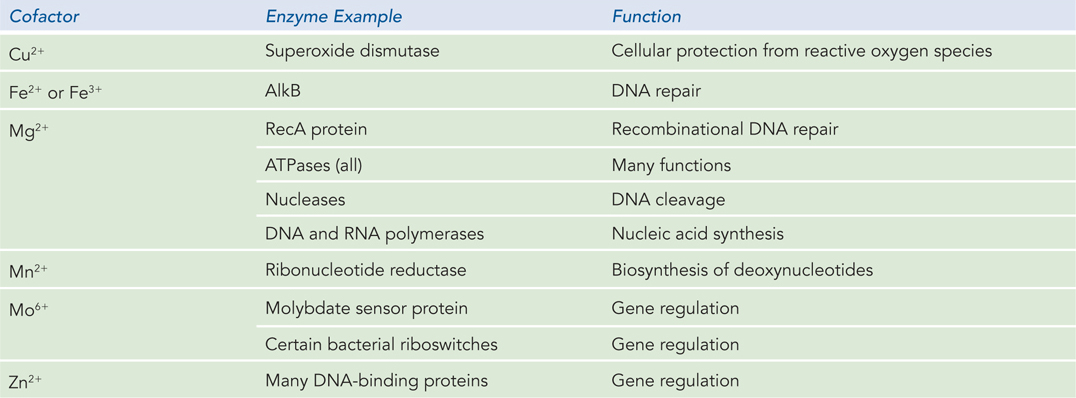
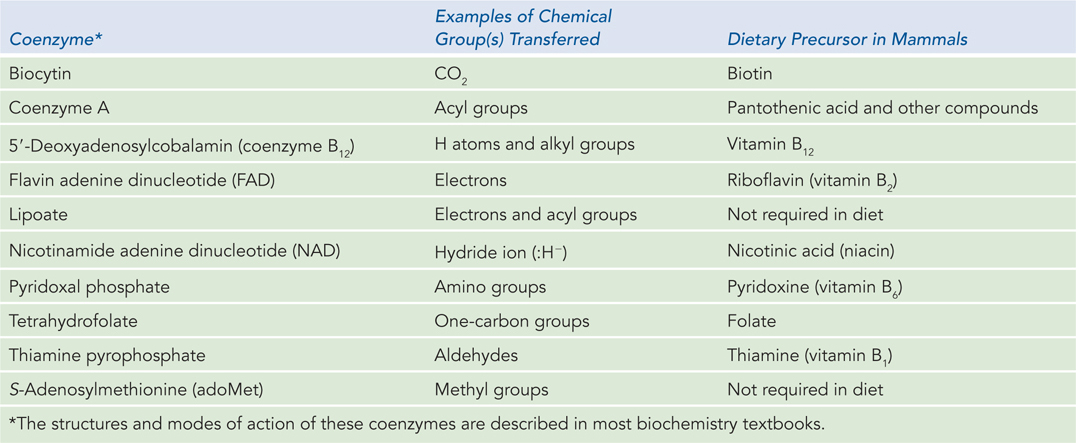
With the exception of a small group of catalytic RNA molecules (described in Chapter 16), all enzymes are proteins. Their catalytic activity depends on the integrity of their native protein conformation. Enzymes, like other proteins, have molecular weights ranging from about 12,000 to more than 1 million. Some enzymes require for their activity no additional chemical groups other than their amino acid residues. Others require an additional chemical component called a cofactor, either one or more inorganic metal ions (Table 5-3) or a complex organic or metallo-
143
An enzyme catalyzes a reaction by providing a specific environment in which the reaction can occur more rapidly. Here are some key principles of enzyme-
A molecule that undergoes an enzyme-
catalyzed reaction is referred to as a substrate. A substrate differs from a ligand in that it can undergo a chemical transformation while bound to the enzyme, whereas a ligand does not. The substrate interacts with the enzyme in a pocket known as the active site (Figure 5-8). The active site is typically lined with multiple chemical groups—
amino acid side chains, metal ion cofactors, and/or coenzymes— all oriented to facilitate the reaction. 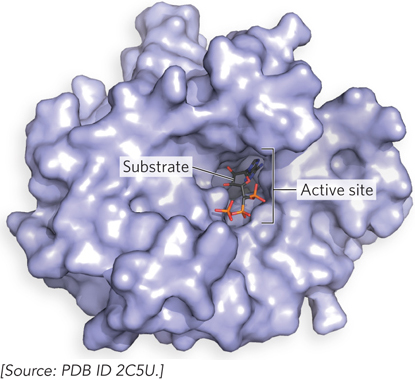 Figure 5-8: Binding of a substrate to an enzyme at the active site. This is the enzyme T4 RNA ligase, with a bound substrate, ATP (stick representation). Active sites are typically pockets in the surface of enzymes.
Figure 5-8: Binding of a substrate to an enzyme at the active site. This is the enzyme T4 RNA ligase, with a bound substrate, ATP (stick representation). Active sites are typically pockets in the surface of enzymes.An enzyme-
catalyzed reaction is highly specific for that particular reaction. An active site that is set up to catalyze one reaction with one substrate will not interact well with other substrates. Specificity is an important property of every enzyme. The catalysis of a different reaction requires a different enzyme. Catalysis often requires conformational flexibility. As we have seen for proteins that reversibly bind ligands, conformational changes have an essential role in enzyme function. Induced fit and cooperativity also play roles in enzyme catalysis.
Many enzymes are regulated. The panoply of enzymes available to a given cell confers the opportunity not just to accelerate reactions but to control them. In this way, cellular metabolism can be modulated as resources and circumstances demand.
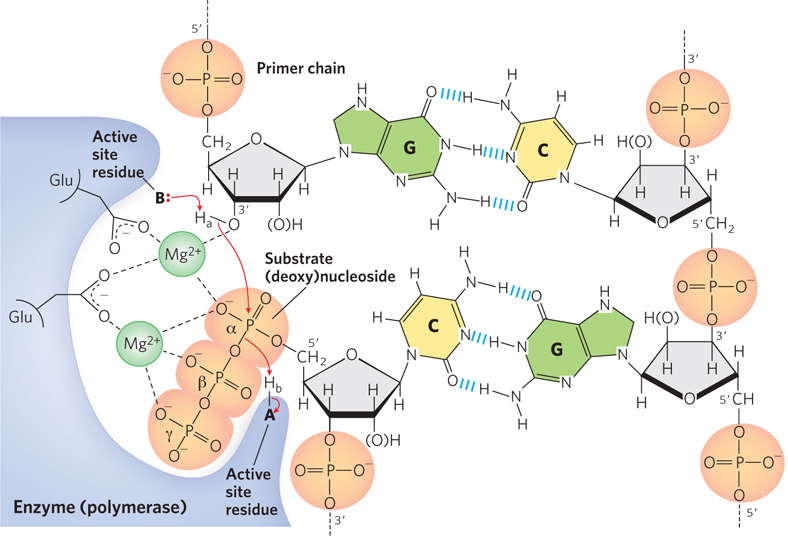
The enormous and highly selective rate enhancements achieved by enzymes can be explained by the many types of covalent and noncovalent interactions between enzyme and substrate. Chemical reactions of many types may take place between substrates and the functional groups (specific amino acid side chains, metal ions, and coenzymes) on enzymes. The particular reactions that occur depend on the requirements of the overall reaction to be catalyzed. An enzyme’s catalytic functional groups may form a transient covalent bond with the substrate and activate it for reaction. Or a group may be transiently transferred from the substrate to the enzyme. The most common type of group transfer involves the transfer of protons between ionizable amino acid side chains in the active site and groups on the substrate molecule, a process called general acid and base catalysis (Figure 5-9). In the enzymes important to molecular biology, phosphoryl group transfers are also common. In many cases, these group transfer reactions occur only in the enzyme active site. The capacity to facilitate multiple interactions and transfers of this type, sometimes all at once, is one of the factors contributing to the rate enhancements provided by enzymes.
144
Covalent interactions are only part of the story, however. Much of the energy required to increase the reaction rate is derived from weak, noncovalent interactions between substrate and enzyme, including hydrogen bonds and hydrophobic and ionic interactions. The formation of each weak interaction is accompanied by the release of a small amount of free energy that stabilizes the interaction. The energy derived from enzyme-
In the context of nucleic acid metabolism, one type of weak interaction merits special mention. Ionic interactions can include interactions between bound metals (such as Mg2+, Mn2+, and Fe2+ or Fe3+ ions) and substrates. About one-
145
Enzymes Increase the Rate of a Reaction by Lowering the Activation Energy
A simple enzyme reaction might be written like this:

where E, S, and P represent the enzyme, substrate, and product, and ES and EP are transient complexes of the enzyme with the substrate and with the product.
To understand catalysis, we must recall the important distinction between reaction equilibria and reaction rates. The equilibrium between S and P reflects the difference in the free energies of their ground states. Any reaction, such as S ⇌ P, can be described by a reaction coordinate diagram, a picture of the energy changes during the reaction (Figure 5-10a). Energy in biological systems is described in terms of free energy, G (see Chapter 3). In the diagram, the free energy of the system is plotted against the progress of the reaction (the reaction coordinate). In this example, the free energy of the ground state of P is lower than that of S, so the biochemical standard free-

KEY CONVENTION
To describe the free-
146
A favorable equilibrium does not mean that the S → P conversion will occur at a fast or even detectable rate. An unfavorable equilibrium does not mean that the reaction will be slow. Instead, the rate of a reaction depends on the height of the energy hill that separates the product from the substrate. At the top of this hill lies the transition state (denoted by ‡ in Figure 5-10a). The transition state is not a stable species but a transient moment when the alteration in the substrate has reached a point corresponding to the highest energy in the reaction coordinate diagram. The difference between the energy levels of the ground state and the transition state is the activation energy, ΔG‡. A higher activation energy corresponds to a slower reaction.
The function of a catalyst is to increase the rate of a reaction. Catalysts do not affect reaction equilibria, and enzymes are no exception. The bidirectional arrows in Equation 5-
Two fundamental and interrelated principles provide a general explanation for how enzymes use noncovalent binding energy to accelerate a reaction:
Much of the catalytic power of an enzyme is ultimately derived from the free energy released in forming many weak bonds and interactions between the enzyme and its substrate. This binding energy contributes to specificity as well as to catalysis.
Weak interactions are optimized in the reaction transition state; enzyme active sites are complementary not to substrates per se but to the transition states through which substrates pass as they are converted to products during the reaction (Figure 5-10b).
When the enzyme active site is complementary to the reaction transition state, some of the noncovalent interactions between enzyme and substrate occur only in the transition state. The free energy (binding energy) released by the formation of these interactions partially offsets the energy required to reach the top of the energy hill. The summation of the unfavorable (positive) activation energy ΔG‡ and the favorable (negative) binding energy ΔGB results in a lower net activation energy (see Figure 5-10a). Even on the enzyme, the transition state is not a stable species but a brief point in time that the substrate spends atop an energy hill. The enzyme-
Covalent interactions can accelerate some enzyme-
The Rates of Enzyme-Catalyzed Reactions Can Be Quantified
The oldest approach to understanding enzyme mechanisms, and the one that remains most important, is to determine the rate of a reaction and how it changes in response to changes in experimental parameters, a discipline known as enzyme kinetics. We provide here a brief review of key concepts related to the kinetics of enzyme-
Substrate concentration affects the rate of enzyme-

147

When the enzyme is first mixed with a large excess of substrate, there is an initial period called the pre-


The curve expressing the relationship between [S] and V0 (see Figure 5-11b) has the same general shape for most enzymes (approaching a rectangular hyperbola). It can be expressed algebraically by an equation developed by Leonor Michaelis and Maud Menten, called the Michaelis-
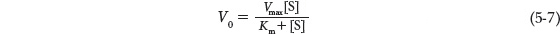
The important terms are [S], V0, Vmax, and a constant called the Michaelis constant, Km. All these terms are readily measured experimentally.
The Michaelis-
148
Kinetic parameters are used to compare enzyme activities. Many enzymes that follow Michaelis-
Figure 5-11b shows a simple graphical method for obtaining an approximate value for Km. The Km, as noted, can vary greatly from enzyme to enzyme, and even for different substrates of the same enzyme. The magnitude of Km is sometimes interpreted (often inappropriately) as an indicator of the affinity of an enzyme for its substrate. However, Km is not equivalent to the substrate Kd (the simple binding equilibrium for the enzyme substrate) for many enzymes.
149
The term Vmax depends on both the concentration of enzyme and the rate of the rate-
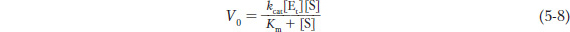
The constant kcat is a first-
In cells, there are many situations in which enzyme activity is inhibited by specific molecules, including other proteins. From a practical standpoint, the development of pharmaceutical and agricultural agents almost always involves the development of inhibitors for particular enzymes. Some aspects of enzyme inhibition are reviewed in Highlight 5-1.
HIGHLIGHT 5-1 A CLOSER LOOK: Reversible and Irreversible Inhibition
Enzyme inhibitors are molecules that interfere with catalysis by slowing or halting enzyme reactions. The two general categories of enzyme inhibition are reversible and irreversible. There are three types of reversible inhibition: competitive, uncompetitive, and mixed.
A competitive inhibitor competes with the substrate for the active site of an enzyme (Figure 1a). While the inhibitor (I) occupies the active site, it prevents binding of the substrate to the enzyme. Many competitive inhibitors are structurally similar to the substrate and combine with the enzyme to form an EI complex, but without leading to catalysis. Even fleeting combinations of this type will reduce the efficiency of the enzyme. The two other types of reversible inhibition, though often defined in terms of one-
All of these inhibition patterns can be analyzed with the aid of a single equation derived from the Michaelis-
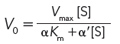
where α and α′ reflect the interaction of an inhibitor with the free enzyme (through KI) and with the ES complex (through  ), respectively. These terms are defined as:
), respectively. These terms are defined as:
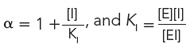
and
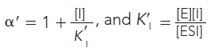
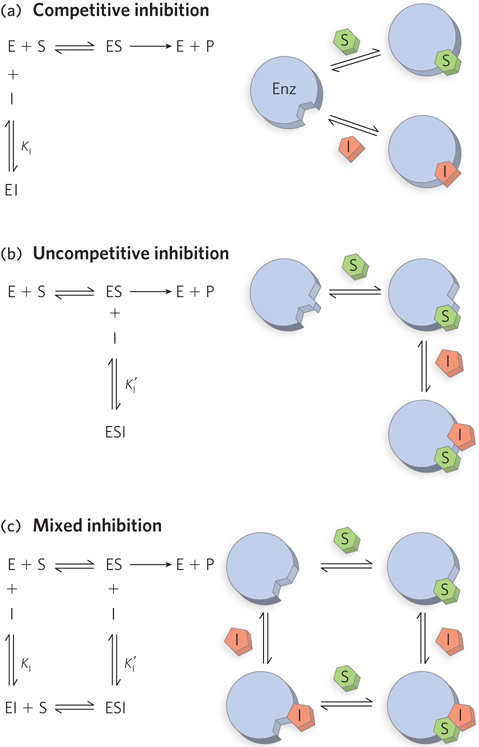
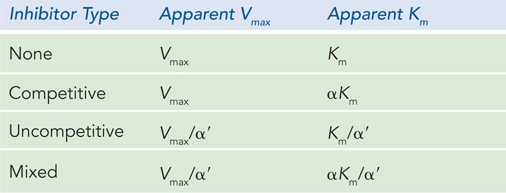
For a competitive inhibitor, there is no binding to the ES complex, and α′ = 1. For an uncompetitive inhibitor, there is no binding to the free enzyme (E), and α = 1. For a mixed inhibitor, both α and α′ are greater than 1. Each class of inhibitor has characteristic effects on the key kinetic parameters in the Michaelis-
Many reversible enzyme inhibitors are used as pharmaceutical drugs; two examples are shown in Figure 2. The human immunodeficiency virus (HIV) encodes a DNA polymerase that can use either RNA or DNA as template; this enzyme is a reverse transcriptase (discussed in Chapter 14). It uses deoxynucleoside triphosphates as substrates, and it is competitively inhibited by the drug AZT—
An irreversible inhibitor can bind covalently with or destroy a functional group on an enzyme that is essential for the enzyme’s activity, or it can form a particularly stable noncovalent association. The formation of a covalent link between an irreversible inhibitor and an enzyme is common. Because the enzyme is effectively inactivated, irreversible inhibitors affect both Vmax and Km. An inhibitor that does not form a covalent link but binds so tightly to the enzyme active site that it does not dissociate within hours or days is also effectively an irreversible inhibitor. Given that enzyme active sites bind most tightly to the transition state of the reactions they catalyze, a molecule that mimics the transition state can be a tight-
Note that uncompetitive and mixed inhibitors should not be confused with allosteric modulators (see Section 5.4). Although the inhibitors bind at a second site on the enzyme, they do not necessarily mediate conformational changes between active and inactive forms, and the kinetic effects are distinct.
150
DNA Ligase Activity Illustrates Some Principles of Catalysis
An understanding of the complete mechanism of action of a purified enzyme requires the identification of all substrates, cofactors, products, and regulators. Moreover, it requires a knowledge of (1) the temporal sequence in which enzyme-
It is impractical, of course, to cover all possible classes of enzyme chemistry, and we focus here on an enzyme reaction important to molecular biology: the reaction catalyzed by DNA ligases. The discussion concentrates on selected principles, along with some key discoveries that have helped bring these principles into focus. We also use the DNA ligase example to review some of the conventions used to depict enzyme mechanisms. Many mechanistic details and pieces of experimental evidence are necessarily omitted; an entire book would be needed to document the rich experimental history of enzyme research.
DNA ligases were discovered in 1967, and reports were published from four different research groups in that year. These enzymes catalyze the joining of DNA ends at strand breaks (also called nicks) that have a phosphorylated 5′ terminus and a 3′ terminus with a free hydroxyl group. In cells, these enzymes provide the critical links between discontinuous segments of replicated DNA (called Okazaki fragments; see Chapter 11) and carry out the final step in most DNA repair reactions (see Chapter 12). Since their discovery, many details of the reaction mechanism of these enzymes have been elucidated. DNA ligases have become essential tools of biotechnology, used by laboratories around the world to covalently join DNA segments to create recombinant DNA (see Chapter 7). RNA ligases have also been characterized; they use a similar reaction mechanism.
DNA ligases make use of two cofactors: Mg2+ ions and either ATP or nicotinamide adenine dinucleotide (NAD+). ATP-
All DNA ligases promote a reaction that involves three chemical steps (Figure 5-12). In step 1, an adenylate group, adenosine 5′-monophosphate (AMP), is transferred from either ATP or NAD+ to a Lys residue in the enzyme active site. This process occurs readily in the absence of DNA. In step 2, the enzyme binds to DNA at the site of a strand break and transfers the AMP to the 5′ phosphate of the DNA strand. This activates the 5′ phosphate for nucleophilic attack by the 3′-hydroxyl group of the DNA, in step 3, leading to displacement of the AMP and formation of a new phosphodiester bond in the DNA that seals the nick. Each of the three steps has a highly favorable reaction equilibrium that renders it effectively irreversible. In the absence of DNA, the adenylated enzyme formed in step 1 is quite stable, and it is likely that most DNA ligases in a cell are already adenylated and ready to react with DNA. In addition to illustrating the reaction pathway, Figure 5-12 introduces the conventions commonly used to describe enzyme-
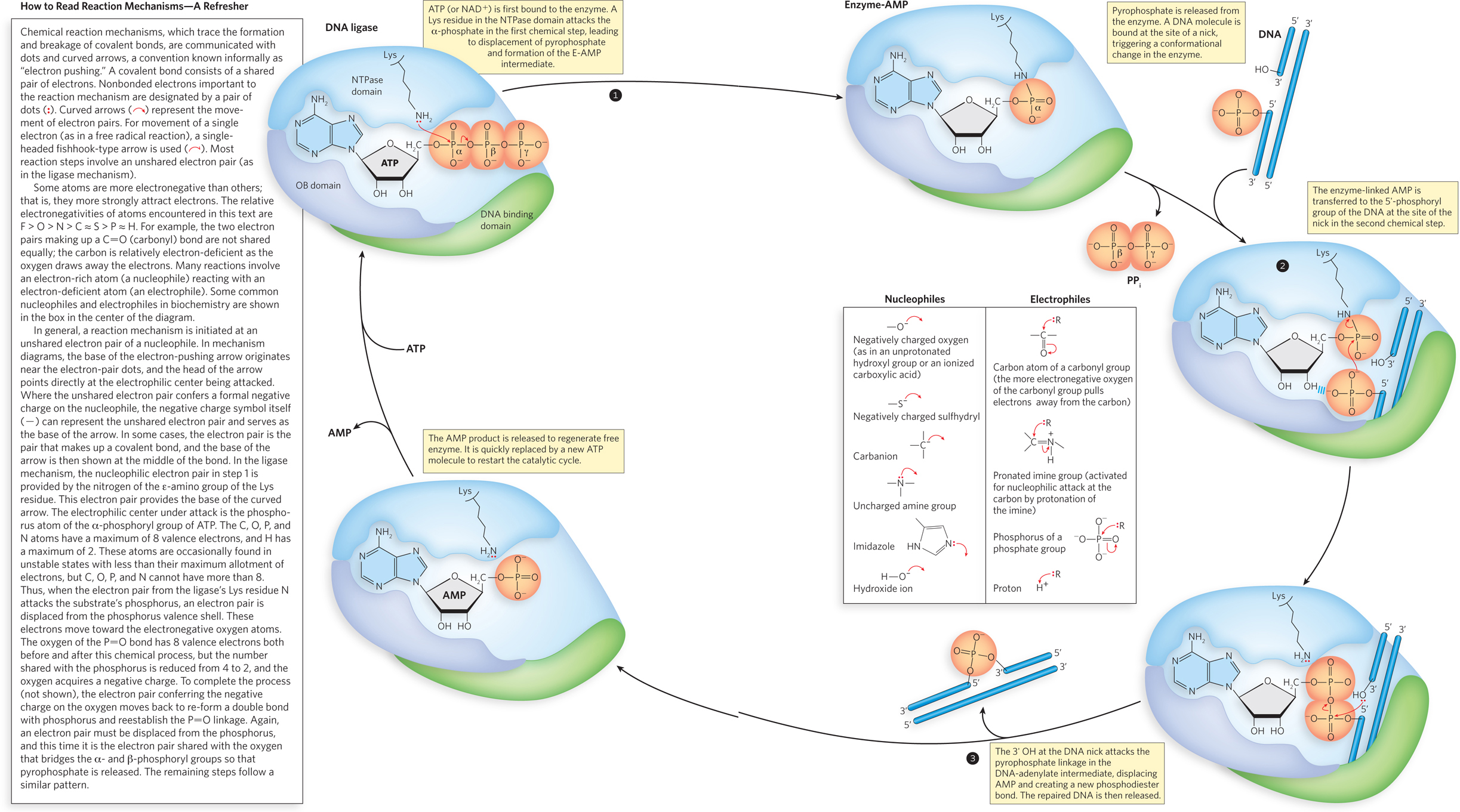
The overall picture of the DNA ligase reaction mechanism is a composite derived from kinetic and structural studies of many closely related enzymes, including those isolated from bacteriophages T4 and T7, bacteria, eukaryotic viruses (that is, viruses with eukaryotic host cells), and mammals. The ligases typically consist of a DNA-
151
This one example cannot provide a complete overview of the broad range of strategies that enzymes use, but it does serve as a good introduction to the complexity of enzyme reaction mechanisms. In addition, it illustrates the transfer of phosphoryl groups, a reaction catalyzed by protein enzymes and RNA enzymes (ribozymes) involved in almost every aspect of molecular biology—
SECTION 5.2 SUMMARY
Most enzymes are proteins. They facilitate the reactions of substrate molecules. The catalyzed reaction occurs in an active site, a pocket on the enzyme that is lined with amino acid side chains and, in many cases, bound cofactors that participate in the reaction.
Enzymes are catalysts. Catalysts do not affect reaction equilibria; they enhance reaction rates by lowering activation energies.
Enzyme catalysis involves both covalent enzyme-
substrate interactions and noncovalent interactions. Enzyme active sites bind most tightly to the transition states of the reactions they catalyze. The rates of most enzyme-
catalyzed reactions are described by the Michaelis- Menten equation, which relates the key kinetic parameters Vmax, Km, and kcat. A DNA ligase catalyzes a series of phosphoryl transfer reactions to seal nicks in the DNA backbone; its reaction mechanism illustrates several general principles of enzyme-
catalyzed reactions.