Section 2.2 Exercises

78

CLARIFYING THE CONCEPTS

Question 2.138

1. Which of the methods for displaying data introduced in this section (frequency and relative frequency distributions, histograms, frequency polygons, stem-and-leaf displays, and dotplots) can be used with both quantitative and qualitative data? Which can be used for quantitative data only? (p. 71)

2.2.1

Both: frequency distribution, relative frequency distribution; quantitative data only: histograms, frequency polygons, stem-and-leaf displays, dotplot.

Question 2.139

2. Describe at least one potential benefit of combining classes when constructing a frequency distribution. Describe at least one potential benefit from retaining a larger number of classes. (p. 62)

Question 2.140

3. In general, how many classes should be used when constructing a frequency distribution? (p. 63)

2.2.3

Between 5 and 20

Question 2.141

4. Describe at least one drawback of choosing class limits that overlap. (p. 64)

Question 2.142

5. Describe at least one way that a dotplot may be useful. (p. 70)

2.2.5

Answers will vary.

Question 2.143

6. In your own words, describe what is meant by “symmetry.” Provide an example of a shape that is symmetric and an example of a shape that is not symmetric. (p. 73)

Question 2.144

7. What are some examples of data sets that are often right-skewed? Left-skewed? (p. 73)

2.2.7

Answers will vary.

Question 2.145

8. True or false: When the objective is to retain complete knowledge of the data set, the best graphical summary to use is the histogram. (p. 75)

PRACTICING THE TECHNIQUES

image CHECK IT OUT!

To do Check out Topic
Exercises
9–12		 Example 9 Frequency and relative
frequency distributions
Exercises
13–16		 Example 10 Frequency distributions using
classes
Exercises
17–40		 Examples
11 and 12 		Class limits, widths, boundaries,
and frequency distributions for
continuous data
Exercises
41–52		 Example 13 Constructing histograms
Exercises
53–56		 Example 14 Frequency polygons
Exercises
57–60		 Example 15 Stem-and-leaf displays
Exercises
61–64		 Example 17 Dotplots
Exercises
65–66		 Example 18 Comparison dotplots
Exercises
67–78		 Example 19 Acquiring information from
graphs and tables
Exercises
79–82		 Example 20 Identifying the shape of the
distribution

Business Insider reported the list of actors in Table 24 who have received more than one Oscar nomination but have never won an Oscar. Use the data to construct the table or graph indicated in Exercises 9 and 10.

Table 2.54: TABLE 24 Oscar nominations for actors who have never won an Oscar
Actor Nominations Actor Nominations
Peter O'Toole 8 Tom Cruise 3
Richard Burton 7 Will Smith 2
Glenn
Close		 6 John
Travolta		 2
Leonardo
DiCaprio		 5 Edward
Norton		 2
Julianne
Moore		 4 Judy
Garland		 2
Sigourney
Weaver		 3 James
Dean		 2
Johnny Depp 3
Table 2.54: Source: www.businessinsider.com/actors-who-have-never-won-oscar-2014-3.

Question 2.146

nooscars

9. Frequency distribution

2.2.9

Number of nominations Frequency Relative frequency
2 5 5/13 = 0.3846
3 3 3/13 = 0.2308
4 1 1/13 = 0.0769
5 1 1/13 = 0.0769
6 1 1/13 = 0.0769
7 1 1/13 = 0.0769
8 1 1/13 = 0.0769
Total 13 13/13 = 1.0000

Question 2.147

nooscars

10. Relative frequency distribution

The data in Table 25 represent the top 18 players in baseball history for the number of career grand slams (home run with the bases loaded). Use the data to construct the table or graph indicated in Exercises 11 and 12.

Table 2.56: TABLE 25 Most career grand slams
Player Grand
slams		 Player Grand
slams
Alex Rodriguez 24 Hank Aaron 16
Lou Gehrig 23 Dave Kingman 16
Manny Ramírez 21 Babe Ruth 16
Eddie Murray 19 Ken Griffey, Jr. 15
Willie McCovey 18 Richie Sexson 15
Robin Ventura 18 Jason Giambi 14
Carlos Lee 17 Gil Hodges 14
Jimmie Foxx 17 Mark McGwire 14
Ted Williams 17 Mike Piazza 14

Question 2.148

grandslams

11. Frequency distribution

2.2.11

Grand slams Frequency Relative frequency
14 4 4/18 = 0.2222
15 2 2/18 = 0.1111
16 3 3/18 = 0.1667
17 3 3/18 = 0.1667
18 2 2/18 = 0.1111
19 1 1/18 = 0.0556
21 1 1/18 = 0.0556
23 1 1/18 = 0.0556
24 1 1/18 = 0.0556
Total 18 18/18 = 1.0000

Question 2.149

grandslams

12. Relative frequency distribution

For Exercises 13 and 14, use the Oscar nomination data from Table 24.

Question 2.150

nooscars

13. Define the following classes: 0-3, 4-6, and 7-9. Use these classes to construct a frequency distribution.

2.2.13

Nominations Frequency Relative frequency
0–3 8 8/13 = 0.6154
4–6 3 3/13 = 0.2308
7–9 2 2/13 = 0.1538
Total 13 13/13 = 1.0000

79

Question 2.151

nooscars

14. Using the classes in the previous exercise, construct a relative frequency distribution.

For Exercises 15 and 16, use the grand slams data from Table 25.

Question 2.152

grandslams

15. Define the following classes: 11–15, 16–20, and 21–25. Use these classes to construct a frequency distribution.

2.2.15

Grand slams Frequency Relative frequency
11–15 6 6/18 = 0.3333
16–20 9 9/18 = 0.5000
21–25 3 3/18 = 0.1667
Total 18 18/18 = 1.0000

Question 2.153

grandslams

16. Using the classes in the previous exercise, construct a relative frequency distribution.

The United States currently maintains a negative trade balance with many countries around the world, meaning that we import more from those countries than we export to them. This tends to increase unemployment here in the United States. The data in Table 26 represent the exports, imports, and trade balance of the United States with a sample of 11 countries, for the month of June 2014.

Table 2.60: TABLE 26 Exports, imports, and trade balance (in $ billions)
Country Exports to Imports
from		 Trade
balance
Brazil 3.5 2.5 1
France 2.8 4 −1.2
Germany 4.5 10 −5.6
India 1.9 3.2 −1.3
Italy 1.2 3.7 −2.4
Japan 5.6 11.3 −5.6
South Korea 3.8 5.6 −1.8
Saudi Arabia 1.7 3.5 −1.8
United Kingdom 4.4 4.4 0
Table 2.60: Source: Foreign Trade Division, U.S. Census Bureau.

Use the exports to data for Exercises 17–20. Use five classes with class widths equal to 1. Define the leftmost class as: 1 to < 2.

Question 2.154

tradebalance

17. Determine the class limits.

2.2.17

1 to < 2, 2 to < 3, 3 to < 4, 4 to < 5, 5 to < 6

Question 2.155

tradebalance

18. Determine the class boundaries.

Question 2.156

tradebalance

19. Construct a frequency distribution.

2.2.19

Exports to Frequency Relative frequency
1 to < 2 3 3/9 = 0.3333
2 to < 3 1 1/9 = 0.1111
3 to < 4 2 2/9 = 0.2222
4 to < 5 2 2/9 = 0.2222
5 to < 6 1 1/9 = 0.1111
Total 9 9/9 = 1.0000

Question 2.157

tradebalance

20. Build a relative frequency distribution.

For Exercises 21–24, use the imports from data from Table 26. Use five classes with class widths equal to 2. Let the leftmost class be: 2 to < 4.

Question 2.158

tradebalance

21. Determine the class limits.

2.2.21

2 to < 4, 4 to < 6, 6 to < 8, 8 to < 10, 10 to < 12

Question 2.159

tradebalance

22. Determine the class boundaries.

Question 2.160

tradebalance

23. Construct a frequency distribution.

2.2.23

Imports from Frequency Relative frequency
2 to < 4 4 4/9 = 0.4444
4 to < 6 3 3/9 = 0.3333
6 to < 8 0 0/9 = 0.0000
8 to < 10 0 0/9 = 0.0000
10 to < 12 2 2/9 = 0.2222
Total 9 9/9 = 1.0000

Question 2.161

tradebalance

24. Build a relative frequency distribution.

For Exercises 25–28, again use the imports from data from Table 26. But this time, use seven classes with class widths equal to 1.5. Let the leftmost class be: 2.0 to < 3.5.

Question 2.162

tradebalance

25. Determine the class limits.

2.2.25

2 to < 3.5, 3.5 to < 5, 5 to < 6.5, 6.5 to < 8, 8 to < 9.5, 9.5 to < 11, 11 to < 12.5

Question 2.163

tradebalance

26. Determine the class boundaries.

Question 2.164

tradebalance

27. Construct a frequency distribution.

2.2.27

Imports from Frequency Relative frequency
2 to < 3.5 2 2/9 = 0.2222
3.5 to < 5 4 4/9 = 0.4444
5 to < 6.5 1 1/9 = 0.1111
6.5 to < 8 0 0/9 = 0.0000
8 to < 9.5 0 0/9 = 0.0000
9.5 to < 11 1 1/9 = 0.1111
11 to < 12.5 1 1/9 = 0.1111
Total 9 9/9 = 1.0000

Question 2.165

tradebalance

28. Build a relative frequency distribution.

For Exercises 29–32, use the trade balance data from Table 26. Use eight classes with class widths equal to 1. Let the leftmost class be: −6 to < −5.

Question 2.166

tradebalance

29. Determine the class limits.

2.2.29

–6 to < –5, –5 to < –4, –4 to < –3, –3 to < –2, –2 to < –1, –1 to < 0, 0 to < 1, 1 to < 2

Question 2.167

tradebalance

30. Determine the class boundaries.

Question 2.168

tradebalance

31. Construct a frequency distribution.

2.2.31

Trade balance Frequency Relative frequency
–6 to < –5 2 2/9 = 0.2222
–5 to < –4 0 0/9 = 0.0000
–4 to < –3 0 0/9 = 0.0000
–3 to < –2 1 1/9 = 0.1111
–2 to < –1 4 4/9 = 0.4444
–1 to < 0 0 0/9 = 0.0000
0 to < 1 1 1/9 = 0.1111
1 to < 2 1 1/9 = 0.1111
Total 9 9/9 = 1.0000

Question 2.169

tradebalance

32. Build a relative frequency distribution.

Table 27 contains the motor vehicle theft rate for the top 20 countries in the world for motor vehicle theft, for 2012. The theft rate equals the number of motor vehicles stolen in 2012 per 100,000 residents.

Table 2.65: TABLE 27 Motor vehicle theft rate for top 20 countries
Country Motor vehicle
theft rate		 Country Motor vehicle
theft rate
Italy 208.0 Trinidad 61.7
France 174.1 Jordan 58.3
USA 167.8 Hungary 56.5
Sweden 117.2 Lithuania 45.7
Belgium 106.0 Slovakia 45.2
Greece 100.2 Latvia 37.8
Norway 94.1 Switzerland 30.9
Netherlands 75.2 Serbia 28.9
Spain 75.1 Austria 27.2
Cyprus 66.0 Barbados 24.0
Table 2.65: Source: United Nations Office on Drugs and Crime.

Use the motor vehicle theft rate data for Exercises 33–36. Use nine classes with class widths equal to 25. Define the leftmost class as: 0 to < 25.

Question 2.170

theftrate20

33. Determine the class limits.

2.2.33

0 to < 25, 25 to < 50, 50 to < 75, 75 to < 100, 100 to < 125, 125 to < 150, 150 to < 175, 175 to < 200, 200 to < 225

Question 2.171

theftrate20

34. Determine the class boundaries.

Question 2.172

theftrate20

35. Construct a frequency distribution.

2.2.35

Motor vehicle theft rate Frequency Relative frequency
0 to < 25 1 1/20 = 0.05
25 to < 50 6 6/20 = 0.30
50 to < 75 4 4/20 = 0.20
75 to < 100 3 3/20 = 0.15
100 to < 125 3 3/20 = 0.15
125 to < 150 0 0/20 = 0.00
150 to < 175 2 2/20 = 0.10
175 to < 200 0 0/20 = 0.00
200 to < 225 1 1/20 = 0.05
Total 20 20/20 = 1.00

Question 2.173

theftrate20

36. Build a relative frequency distribution.

For Exercises 37–40, again use the motor vehicle theft rate data from Table 27. But this time, use eight classes with class widths equal to 25. Define the leftmost class as: 20 to < 45.

Question 2.174

37. Determine the class limits.

2.2.37

20 to < 45, 45 to < 70, 70 to < 95, 95 to < 120, 120 to < 145, 145 to < 170, 170 to < 195, 195 to < 220

Question 2.175

38. Determine the class boundaries.

Question 2.176

39. Construct a frequency distribution.

2.2.39

Motor vehicle theft rate Frequency Relative frequency
20 to < 45 5 5/20 = 0.25
45 to < 70 6 6/20 = 0.30
70 to < 95 3 3/20 = 0.15
95 to < 120 3 3/20 = 0.15
120 to < 145 0 0/20 = 0.00
145 to < 170 1 1/20 = 0.05
170 to < 195 1 1/20 = 0.05
195 to < 220 1 1/20 = 0.05
Total 20 20/20 = 1.00

Question 2.177

40. Build a relative frequency distribution.

For Exercises 41 and 42, use the exports to data from Table 26. Construct the indicated histogram using five classes with class widths equal to 1. Your work from Exercises 17–20 should be helpful.

80

Question 2.178

41. Frequency histogram

2.2.41

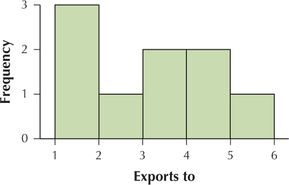
image

Question 2.179

42. Relative frequency histogram

For Exercises 43 and 44, use the imports from data from Table 26. Construct the indicated histogram, using five classes with class widths equal to 2. Your work from Exercises 21–24 should be helpful.

Question 2.180

43. Frequency histogram

2.2.43

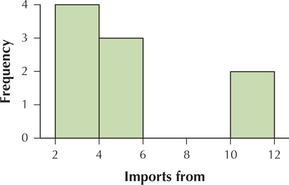
image

Question 2.181

44. Relative frequency histogram

For Exercises 45 and 46, again use the imports from data from Table 26. This time, construct the indicated histogram using seven classes with class widths equal to 1.5. Use your work from Exercises 25–28.

Question 2.182

45. Frequency histogram

2.2.45

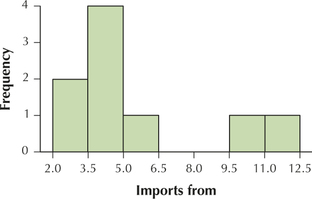
image

Question 2.183

46. Relative frequency histogram

For Exercises 47 and 48, use the trade balance data from Table 26. Construct the indicated histogram, this time using eight classes with class widths equal to 1. Use your work from Exercises 29–32.

Question 2.184

47. Frequency histogram

2.2.47

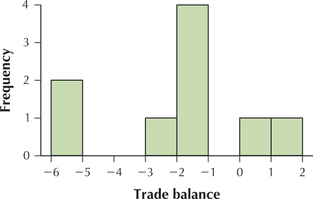
image

Question 2.185

48. Relative frequency histogram

For Exercises 49 and 50, use the motor vehicle theft rate data from Table 27. Construct the indicated histogram, using nine classes with class widths equal to 25. Use your work from Exercises 33–36.

Question 2.186

49. Frequency histogram

2.2.49

image

Question 2.187

50. Relative frequency histogram

For Exercises 51 and 52, again use the motor vehicle theft rate data from Table 27. But this time, construct the indicated histogram, using eight classes with class widths equal to 25. Use your work from Exercises 37–40.

Question 2.188

51. Frequency histogram

2.2.51

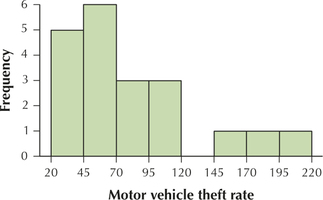
image

Question 2.189

52. Relative frequency histogram

For Exercises 53–56, construct a frequency polygon with the indicated data.

Question 2.190

53. The exports to data from Table 26. Calculate the midpoints using five classes with class width equal to 1.

2.2.53

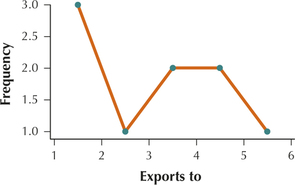
image

Question 2.191

54. The imports from data from Table 26. Get the midpoints using five classes with class width equal to 2.

Question 2.192

55. The imports from data from Table 26. But this time compute the midpoints using seven classes with class width equal to 1.5.

2.2.55

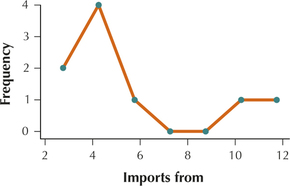
image

Question 2.193

56. The motor vehicle theft rate data from Table 27. Calculate the midpoints using nine classes with class widths equal to 25.

For Exercises 57–60, construct a stem-and-leaf display of the indicated data.

Question 2.194

57. Exports to data from Table 26.

2.2.57

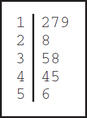
image

Question 2.195

58. Imports from data from Table 26.

Question 2.196

59. Trade balance data from Table 26.

2.2.59

image

Question 2.197

60. Motor vehicle theft rate data from Table 27.

For Exercises 61–64, construct a dotplot of the indicated data.

Question 2.198

61. Exports to data from Table 26.

2.2.61

image

Question 2.199

62. Imports from data from Table 26.

Question 2.200

63. Trade balance data from Table 26.

2.2.63

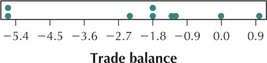
image

Question 2.201

64. Motor vehicle theft rate data from Table 27.

For Exercises 65 and 66, construct a comparison dotplot of the indicated data.

Question 2.202

65. Exports to data and imports from data from Table 26.

2.2.65

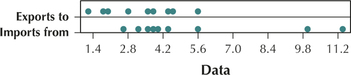
image

Question 2.203

66. Exports to data and trade balance data from Table 26.

The cost of the last music download (in dollars) for 100 college students is summarized in Figure 43. Use this information for Exercises 67–70.

image
Figure 2.43: FIGURE 43 Cost of music download.

Question 2.204

67. What are the class midpoints?

2.2.67

0.75, 2.25, 3.75, 5.25, 6.75, 8.25, 9.75, 11.25

Question 2.205

68. About how many students paid less than $1.50 for their last music download? What is the relative frequency?

Question 2.206

69. About how many students paid $10.50 or more on their last music download?

2.2.69

2, 0.02

Question 2.207

70. Use your answers to the last two questions to estimate about how many students paid between $1.50 and $10.50 for their last music download.

Figure 44 shows a histogram of a set of statistics quiz scores. Use this information for Exercises 71–74.

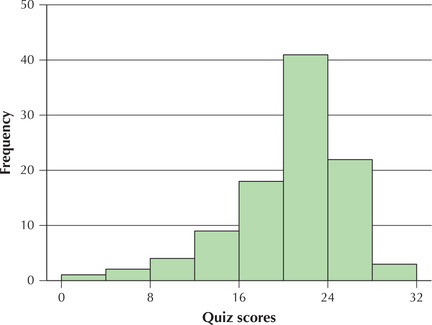
image
Figure 2.44: FIGURE 44 Quiz scores.

81

Question 2.208

71. What are the class midpoints?

2.2.71

2, 6, 10, 14, 18, 22, 26, 30

Question 2.209

72. Between which two scores did the most quiz scores occur?

Question 2.210

73. Can we tell what the highest grade on the quiz was? Why or why not? Would a stem-and-leaf display of this data be able to tell us what the highest grade was?

2.2.73

No. The histogram does not tell us the actual quiz scores. Yes.

Question 2.211

74. Estimate the relative frequency of quiz scores below 8.

Figure 45 shows a histogram of a set of women's heights. Use this information for Exercises 75–78.

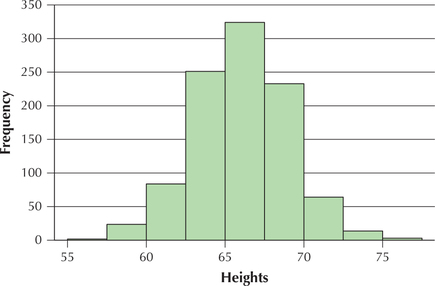
image
Figure 2.45: FIGURE 45 Women's heights.

Question 2.212

75. Calculate the class midpoints.

2.2.75

56.25, 58.75, 61.25, 63.75, 66.25, 68.75, 71.25, 73.75, 76.25

Question 2.213

76. Between which two values did the most heights occur?

Question 2.214

77. If we added one inch to every woman's height, how would Figure 45 change?

2.2.77

The scale on the -axis would shift up by 1 inch.

Question 2.215

78. If we added one inch to every woman's height, which aspects of Figure 45 would stay the same?

For Exercises 79–82, identify the shape of the distribution as either symmetric, right-skewed, or left-skewed.

Question 2.216

79. The data represented in Figure 43.

2.2.79

Right-skewed

Question 2.217

80. The distribution of the data in Figure 44.

Question 2.218

81. The data represented in Figure 45.

2.2.81

Symmetric

Question 2.219

82. The data from Table 19 on page 61.

APPLYING THE CONCEPTS

Question 2.220

fruitcups

83. Fruit Cup Sales for the Student-Run Café. Table 28 contains the number of fruit cups sold per day for the Student-Run café business.

Table 2.68: TABLE 28 Fruit cups sold per day
1 1 1 1 2 2
0 2 2 4 2 2
0 1 2 1 1 1
3 2 2 4 0 0
2 3 3 0 4 4
2 0 1 2 1 3
2 1 3 2 2 1
0 2 0 3 2
  1. Construct a frequency distribution and a relative frequency distribution similar to Table 18.
  2. Use the following classes to construct a frequency distribution and a relative frequency distribution using classes, similar to Table 19. Use the following classes: 0–1, 2–3, 4–5.
  3. What is the relative frequency of days that three or more fruit cups were sold? Did you use your work from (a) or (b) to answer this? Explain how we could not have used the distributions in (b) to answer this.

2.2.83

(a)

Fruit cups sold per day Frequency Relative frequency
0 8 8/47 = 0.1702
1 12 12/47 = 0.2553
2 17 17/47 = 0.3617
3 6 6/47 = 0.1277
4 4 4/47 = 0.0851
Total 47 47/47 = 1.0000

(b)

Fruit cups sold per day Frequency Relative frequency
0–1 20 20/47 = 0.4255
2–3 23 23/47 = 0.4894
4–5 4 4/47 = 0.0851
Total 47 47/47 = 1.0000

(c) 0.2128, (a), Since 2 and 3 fruit cups sold per day are grouped together, we don't know how many of the days had 3 fruit cups sold that day.

Question 2.221

sandwiches

84. Sandwich Sales for the Student-Run Café. Table 29 shows the number of sandwiches sold per day for the Student-Run café business.

Table 2.71: TABLE 29 number of sandwiches sold
5 6 8 4 3 7
6 0 3 2 3 4
9 1 3 8 7 8
2 3 8 6 4 4
6 7 6 5 2 3
8 4 4 6 7 3
5 2 4 8 4 6
1 2 6 4 4
  1. Construct a frequency distribution and a relative frequency distribution similar to Table 18.
  2. Use the following classes to construct a frequency distribution and a relative frequency distribution using classes, similar to Table 19. Use the following classes: 0–2, 3–5, 6–8, 9–11.
  3. Would you say that the distributions in (b) are symmetric? Explain.
  4. What is the proportion (relative frequency) of days that fewer than six sandwiches were sold?

Question 2.222

brooklynfrauds2000

85. Frauds in brooklyn in 2000. Table 30 provides the number of misdemeanor fraud cases in each of Brooklyn's 23 police precincts in 2000.

Table 2.72: TABLE 30 Fraud cases in Brooklyn precincts, 2000
Precinct Frauds Precinct Frauds
40 60 75 198
41 198 76 45
42 92 77 83
43 109 78 33
44 79 79 156
45 240 81 69
46 130 83 78
47 89 84 54
48 210 88 107
49 89 90 45
50 103 94 46
52 95

82

  1. Use 7 classes of width 40 each, starting at the leftmost class: 0 to < 40. Find the frequencies for each class.
  2. Find the relative frequencies for each class.
  3. Construct a frequency histogram of the number of fraud cases in Brooklyn in 2000.
  4. Construct a relative frequency histogram of the number of fraud cases in Brooklyn in 2000.

2.2.85

(a) and (b)

Frauds Frequency Relative frequency
0 to < 40 1 1/23 = 0.0435
40 to < 80 8 8/23 = 0.3478
80 to < 120 8 8/23 = 0.3478
120 to < 160 2 2/23 = 0.0870
160 to < 200 2 2/23 = 0.0870
200 to < 240 1 1/23 = 0.0435
240 to < 280 1 1/23 = 0.0435
Total 23 23/23 = 1.0000

(c)

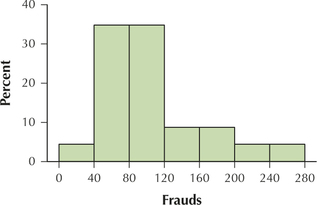
image

(d)

image

image Frauds in Brooklyn in 2013.

Table 31 provides the number of misdemeanor fraud cases in each of Brooklyn's 23 police precincts in 2013. Use this data for Exercises 86–90.

Table 2.74: TABLE 31 Fraud cases in Brooklyn precincts, 2013
Precinct Frauds Precinct Frauds
60 33 75 133
61 53 76 19
62 76 77 41
63 52 78 15
66 23 79 63
67 57 81 36
68 44 83 68
69 16 84 41
70 42 88 48
71 73 90 51
72 27 94 21
73 90

Question 2.223

brooklynfrauds2013

86. Constructing and comparing histograms. Do the following:

  1. Use 7 classes of width 40 each, starting at the leftmost class: 0 to < 40. Find the class boundaries.
  2. Find the frequencies for each class.
  3. Find the relative frequencies for each class.
  4. Construct a frequency histogram of the number of fraud cases in Brooklyn in 2013.
  5. Construct a relative frequency histogram of the number of fraud cases in Brooklyn in 2013.
  6. Compare your frequency histograms from Exercises 85c and 86d. Describe any differences between the two graphs. Do you think this represents good news, bad news, or no news?

Question 2.224

brooklynfrauds2013

87. Getting information from histograms. Refer to your work from Exercise 86 to answer the following questions.

  1. Find the relative frequency of precincts where 80 or more frauds occurred.
  2. Compute the proportion (relative frequency) of precincts where 40 or more frauds occurred.
  3. Compute the relative frequency of precincts that had fewer than 40 frauds. Explain how you could have used your answer from (b) to calculate this.

2.2.87

(a) 0.0870 (b) 0.6522 (c) 0.3478, 1 – 0.6522 = 0.3478

Question 2.225

brooklynfrauds2013

88. Constructing Frequency Polygons. Use Table 31 to answer the following:

  1. Using the same class boundaries you calculated in Exercise 86, find the class midpoints.
  2. Construct a frequency polygon of the number of misdemeanor fraud cases in Brooklyn in 2013.
  3. Use (b) to construct a relative frequency polygon.
  4. Use the relative frequency polygon to find the relative frequency of precincts where more than 100 frauds occurred.

Question 2.226

brooklynfrauds2013

89. Stem-and-leaf Displays. Use Table 31 to answer the following:

  1. Construct a stem-and-leaf display of the number of frauds in Brooklyn in 2013.
  2. Build a split-stem stem-and-leaf display of the number of frauds.
  3. Using the stem-and-leaf display, find how many precincts had 52 or more frauds. Explain whether this could have been found using the histogram from Exercise 86.

2.2.89

(a)

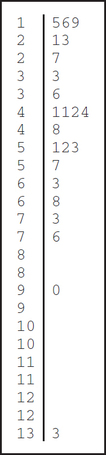
image

(b)

image

(c) 9. Could not have used histogram because the histogram does not contain the actual data.

Question 2.227

brooklynfrauds2013

90. Dotplots. Use Tables 30 and 31 for the following:

  1. Make a dotplot of the number of frauds in Brooklyn in 2013.
  2. Construct a comparison dotplot of the number of frauds in Brooklyn in 2000 and in 2013.
  3. Describe any differences between the two distributions in (b).

Question 2.228

coffees

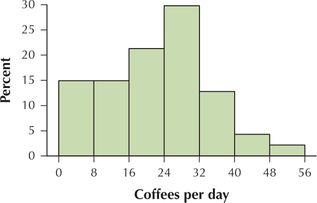
91. Coffee Sales for the Student-Run Café. In Table 32, we see the number of coffees sold per day for the Student-Run café business. Consider this to be continuous data.

Table 2.75: TABLE 32 Coffees sold per day
41 30 21 25 21 4
33 27 28 35 8 13
34 30 23 33 8 4
27 27 31 35 4 16
20 26 29 16 4 14
23 24 48 24 3 10
32 18 25 20 5 11
31 22 31 11 6
  1. Use 7 classes of width 8 each, starting with the following leftmost class: 0 to < 8. Calculate the class boundaries.
  2. Find the frequencies for each class.
  3. Find the relative frequencies for each class.
  4. Construct a frequency histogram of coffees sold.
  5. Construct a relative frequency histogram of coffees sold.

83

2.2.91

(a), (b), (c)

Coffee sold per day Frequency Relative frequency
0 to < 8 7 7/47 = 0.1489
8 to < 16 7 7/47 = 0.1489
16 to < 24 10 10/47 = 0.2128
24 to < 32 15 15/47 = 0.3191
32 to < 40 6 6/47 = 0.1277
40 to < 48 1 1/47 = 0.0213
48 to < 56 1 1/47 = 0.0213
Total 47 47/47 = 1.0000

(d)

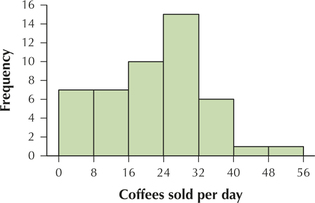
image

(e)

image

Question 2.229

sodas

92. Soda Sales for the Student-Run Café. In Table 33, we see the number of sodas sold per day for the Student-Run café business. Consider this to be continuous data.

Table 2.77: TABLE 33 Sodas sold per day
20 12 24 25 43 45
13 19 31 36 24 50
23 33 15 33 48 26
13 20 26 37 35 26
13 29 39 22 33 55
33 14 24 36 24 42
15 17 35 54 30 45
27 31 11 34 50
  1. Use 10 classes of width 5 each, starting with the following leftmost class: 10 to < 15. Calculate the class boundaries.
  2. Find the frequencies for each class.
  3. Find the relative frequencies for each class.
  4. Construct a frequency histogram of sodas sold.
  5. Construct a relative frequency histogram of sodas sold.

Question 2.230

93. Coffee Sales. Refer to your work from Exercise 91 to answer the following questions.

  1. Find the relative frequency of days that more than 39 coffees were sold.
  2. Compute the proportion (relative frequency) of days that more than 31 coffees were sold.
  3. Compute the relative frequency of days that 31 or fewer coffees were sold. Explain how you could have used your answer from (b) to calculate this.
  4. Find the proportion of days that between 16 and 31 coffees (inclusive) were sold.

2.2.93

(a) 0.0426 (b) 0.1702 (c) 0.8298; 1 – 0.1702 = 0.9298 (d) 0.5319

Question 2.231

94. Soda Sales. Refer to your work from Exercise 92 to answer the following questions.

  1. Find the relative frequency of days that more than 34 sodas were sold.
  2. Find the relative frequency of days that fewer than 20 sodas were sold.
  3. Compute the proportion (relative frequency) of days that 20 or more sodas were sold. Explain how you could have used your answer from (b) to calculate this.
  4. Find the proportion of days that between 20 and 39 sodas (inclusive) were sold.

Question 2.232

95. Coffee Sales. Use Table 32 to answer the following:

  1. Use 7 classes of width 8 each, starting with the following leftmost class: 0 to < 8. Use the class boundaries you calculated in Exercise 91. Find the class midpoints.
  2. Construct a frequency polygon of the number of coffees sold.
  3. Use (b) to construct a relative frequency polygon of the number of coffees sold.
  4. Use the relative frequency polygon to find the relative frequency of days that fewer than 17 coffees were sold.

2.2.95

(a) 4, 12, 20, 28, 36, 44, 52

(b)

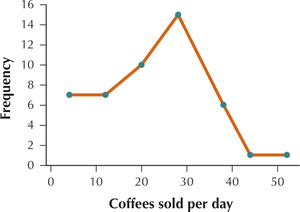
image

(c)

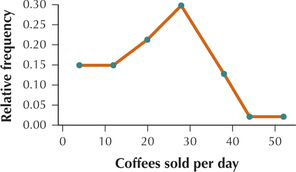
image

(d) 0.3404

Question 2.233

96. Soda Sales. Use Table 33 to answer the following:

  1. Use 10 classes of width 5 each, starting with the following leftmost class: 10 to < 15. Use the class boundaries you calculated in Exercise 92. Find the class midpoints.
  2. Construct a frequency polygon of the number of sodas sold.
  3. Use (b) to construct a relative frequency polygon of the number of sodas sold.
  4. Use the relative frequency polygon to find the relative frequency of days that more than 24 sodas were sold.

Question 2.234

97. Coffee Sales. Use Table 32 to answer the following:

  1. Construct a stem-and-leaf display of the number of coffees sold.
  2. Build a split-stem stem-and-leaf display of the number of coffees sold.
  3. Make a dotplot of the number of coffees sold.
  4. Using the stem-and-leaf display, find the number of days that 28 or more coffees were sold. Explain whether this could have been found using the histogram from Exercise 91.

2.2.97

(a)

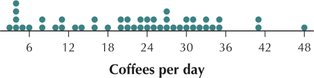
image

(b)

image

(c)

image

(d) 15. No, the stem-and-leaf display contains the actual data.

Question 2.235

98. Soda Sales. Use Table 33 to answer the following:

  1. Construct a stem-and-leaf display of the number of sodas sold.
  2. Build a split-stem stem-and-leaf display of the number of sodas sold.
  3. Make a dotplot of the number of sodas sold.
  4. Using the stem-and-leaf display, find the number of days that 32 or more sodas were sold. Explain whether this could have been found using the histogram from Exercise 92.

Question 2.236

99. Best-selling video games. Figure 46 contains a histogram of the top 30 best-selling video game sales for the week of May 17, 2014. Use Figure 46 to answer the following:

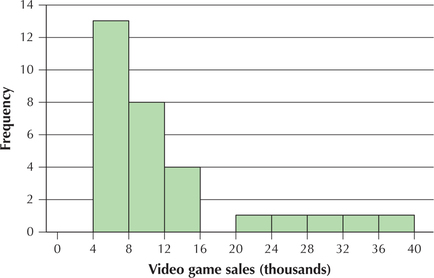
image
Figure 2.46: FIGURE 46 Histogram of video game sales.
  1. Identify whether the distribution is symmetric, left-skewed, or right-skewed. Explain your answer.
  2. Use the histogram to construct a relative frequency histogram.
  3. Explain whether we could use the information in Figure 46 to construct a stem-and-leaf display of video game sales.

2.2.99

(a) Right-skewed, tail on right

(b)

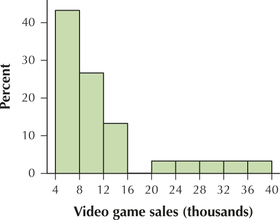
image

(c) No. Histogram does not contain actual data.

84

Question 2.237

100. Small businesses. The U.S. Census Bureau tracks the number of small businesses per city. The accompanying frequency polygon represents the numbers of small businesses per city (in thousands) for 266 cities nationwide.

  1. What is the class width?
  2. What is the lower class limit of the leftmost class? (Hint: Don't forget about the units.)
  3. Which class has the highest frequency?
  4. Which class has the lowest frequency?
image

Question 2.238

101. Refer to the frequency polygon of small businesses per city.

  1. About how many cities have between 1000 and 3000 small businesses?
  2. About how many cities have more than 19,000 small businesses?
  3. About how many cities have between 9000 and 11,000 small businesses?

2.2.101

(a) Approximately 72 (b) Approximately 2 (c) Approximately 18

Question 2.239

countrycont

102. Countries and Continents. Suppose we are interested in analyzing the variable continent for the 10 countries in Table 34. Construct each of the following tabular or graphical summaries. If not appropriate, explain clearly why we can't use that method.

Table 2.78: TABLE 34 Countries and continents
Country Continent
Iraq Asia
United States North America
Pakistan Asia
Canada North America
Madagascar Africa
North Korea Asia
Chile South America
Bulgaria Europe
Afghanistan Asia
Iran Asia
  1. Frequency distribution
  2. Relative frequency distribution
  3. Frequency histogram
  4. Dotplot
  5. Stem-and-leaf display
image

Question 2.240

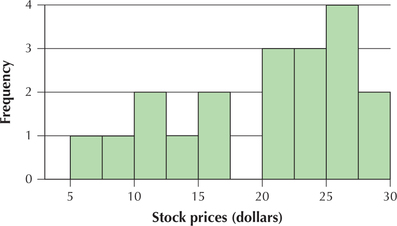
103. Stock Prices. Refer to the histogram of stock prices of 19 technology firms.

  1. How could we turn this into a relative frequency histogram? Would the classes or the rectangles be affected?
  2. Suppose we were given a relative frequency histogram instead. How could we turn it into a frequency histogram?
  3. What is the sample size?

2.2.103

(a) Divide the frequency values by the total frequency—classes not affected (b) change the scale along the relative frequency (vertical) axis by multiplying the relative frequency values by the total frequency—shape of distribution not affected (c) 19

Question 2.241

104. Refer to the histogram of stock prices.

  1. How many stocks were priced above $27.50?
  2. What is the relative frequency of stocks priced above $27.50?
  3. How many stocks had a price below $15?
  4. What is the relative frequency of stocks with a price below $15?

Question 2.242

105. Refer to the histogram of stock prices.

  1. How many stocks are priced between $17.50 and $20?
  2. What is the relative frequency of stocks priced below $5?
  3. Which class has the largest relative frequency? Calculate this relative frequency.
  4. What is the frequency of stocks priced between $10 and $14.99?
  5. How many stocks had a price of $40?

2.2.105

(a) 0 (b) 0 (c) $25 to $27.5 has the largest relative frequency, 4/19 = 0.2105. (d) 3 (e) 0

Question 2.243

106. Would you characterize the shape of the stock prices distribution as (a) tending to be symmetric, (b) tending to be right-skewed, or (c) tending to be left-skewed?

Question 2.244

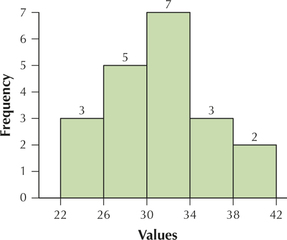
107. Stem-and-Leaf Display. Refer to the accompanying stem-and-leaf display. Reconstruct the data set.

image

2.2.107

Data set: 23 24 25 26 27 28 28 29 30 31 31 32 32 32 33 35 36 37 39 40

85

Question 2.245

108.Refer to the stem-and-leaf display in Exercise 107. Construct a relative frequency distribution, using appropriate values for the class width and the lower class limit of the leftmost class.

Question 2.246

109. Refer to the stem-and-leaf display in Exercise 107. Construct a frequency histogram.

2.2.109

Histogram with five classes

image

Question 2.247

110. Refer to the stem-and-leaf display in Exercise 107. Construct a dotplot.

Question 2.248

111. Frequency Polygon. The following frequency polygon represents the quiz scores for a course in introductory statistics.

image
  1. What is the class width?
  2. What is the lower class limit of the class that has 45 as its midpoint?
  3. What is the upper class limit of the class that has 45 as its midpoint?
  4. Which class has the highest frequency?
  5. Which class has the lowest frequency?

2.2.111

(a) 15 (b) 37.5 (c) 52.5 (d) 67.5 to 82.5 (e) 22.5 to 37.5

Question 2.249

112. Refer to the frequency polygon of quiz scores.

  1. About how many students scored higher than 82.5?
  2. About how many students scored lower than 52.5?
  3. Can we say how many students scored in the 90s? Why or why not?

WORKING WITH LARGE DATA SETS

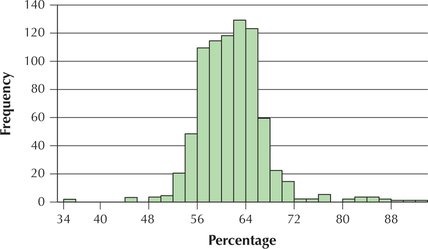
New York Townspeople. Use the following information for Exercises 113–116. For towns in New York State, the following histogram provides information on the percentage of the townspeople who are between 18 and 65 years old.

image

Question 2.250

newyork

113.Would you characterize the distribution as left-skewed, right-skewed, or fairly symmetrical?

2.2.113

Fairly symmetrical

Question 2.251

newyork

114. Provide an estimate of the “typical” percentage of townspeople who are between 18 and 65 years old. Is this typical value near the middle or near one of the “tails” of the distribution?

Question 2.252

newyork

115. Provide a rough estimate of the sample size.

2.2.115

.

Question 2.253

newyork

116. Would it be possible to construct a stem-and-leaf display using the information from the histogram? Explain.

Number of Businesses. Use the following data for Exercises 117–120. The data represent the number of business establishments in a sample of states.

State Businesses
(1000s)		 State Businesses
(1000s)
Alabama 3.8 Michigan 7.5
Arizona 7.9 Minnesota 6.1
Colorado 8.9 Missouri 5.9
Connecticut 3.1 Ohio 9.5
Georgia 10.3 Oklahoma 3.8
Illinois 11.9 Oregon 5.4
Indiana 5.6 South Carolina 4.6
Iowa 2.7 Tennessee 5.4
Maryland 5.7 Virginia 8.6
Massachusetts 6.3 Washington 9.3
Table 2.79: Source: U.S. Census Bureau.

Question 2.254

statebusinesses

117. Construct the following:

  1. A frequency distribution
  2. A relative frequency distribution
  3. A relative frequency histogram

2.2.117

(a) and (b)

Businesses (1000s) Frequency Relative frequency
2 to < 3 1 1/20 = 0.05
3 to < 4 3 3/20 = 0.15
4 to < 5 1 1/20 = 0.05
5 to < 6 5 5/20 = 0.25
6 to < 7 2 2/20 = 0.10
7 to < 8 2 2/20 = 0.10
8 to < 9 2 2/20 = 0.10
9 to < 10 2 2/20 = 0.10
10 to < 11 1 1/20 = 0.05
11 to < 12 1 1/20 = 0.05
Total 20 20/20 = 1.00

(c)

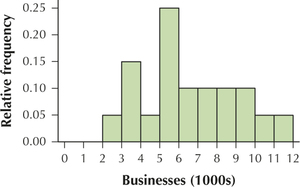
image

Question 2.255

statebusinesses

118. Construct the following:

  1. A dotplot
  2. A frequency polygon
  3. A stem-and-leaf display

Question 2.256

statebusinesses

119. Compare and contrast the relative usefulness of each of four graphical presentation methods—dotplot, histogram, stem-and-leaf display, and frequency polygon—if our primary objective is to

  1. assess symmetry and skewness.
  2. be able to construct it quickly using paper and pencil.
  3. retain complete knowledge of the data set.
  4. give a presentation to people who have never taken a stats course.

2.2.119

Dotplot Histogram Stem-and-leaf Frequency polygon
(a) Symmetry and skewness Appropriate to use for small ranges of data Appropriate to use Appropriate to use for small ranges of data Appropriate to use
(b) Construct using pencil and paper Easily done for small ranges of data Easily done for small ranges of data Easily done for small ranges of data Easily done for small ranges of data
(c) Retain complete knowledge of the data Appropriate Appropriate only if the data are ungrouped Appropriate Appropriate only if the data are ungrouped
(d) Presentation in front of non-statisticians Appropriate Appropriate Appropriate Appropriate

Question 2.257

statebusinesses

image 120. What if we subtract the same amount (say, 1000) from each state's number of businesses. Explain how this would affect the following: What would change? What would stay the same?

  1. Relative frequency histogram
  2. Dotplot
  3. Stem-and-leaf display
  4. Frequency polygon

86

WORKING WITH LARGE DATA SETS

Fats and Cholesterol. For Exercises 121–125, use your knowledge of technology. Open the Nutrition data set.

Question 2.258

nutrition

121. How many observations are there in the data set? How many variables?

2.2.121

961; 25

Question 2.259

nutrition

122. The variable fat contains the fat content in grams for each food. Construct a histogram of fat. Comment on the symmetry or the skewness of the histogram.

Question 2.260

nutrition

123. Is there a particular type of food with a fat content that is particularly large? Which type of food item (or set of similar food items) is this?

2.2.123

Yes; fats and oils.

Question 2.261

nutrition

124. The variable cholesterol contains the cholesterol content in milligrams for each food. Construct a histogram of cholesterol. Comment on the symmetry or the skewness of the histogram.

Question 2.262

nutrition

125. Which food item (or set of similar food items) is highest in cholesterol?

2.2.125

One whole cheesecake (2053 grams of cholesterol)

image Earthquakes. Use the One Variable Statistics and Graphs applet for Exercises 126–131. Work with the Earthquakes data set, which shows the magnitude on the Richter scale of 57 earthquakes that occurred during the week of October 15–22, 2007.

Question 2.263

earthquakes

126. Click on the histogram tab.

  1. How many classes are included in the histogram?
  2. What is the class width?

Question 2.264

earthquakes

127. Click on the leftmost rectangle in the histogram.

  1. What is the frequency for this class?
  2. What are the lower and upper class limits?

2.2.127

(a) 2 (b) 4.00, 4.30

Question 2.265

earthquakes

128. Click on the number line and drag slowly all the way to the left.

  1. What happens to the number of classes as you drag to the left?
  2. What happens to the class widths as you drag to the left?

Question 2.266

earthquakes

129. Click on the number line and drag slowly all the way to the right.

  1. What happens to the number of classes as you drag to the right?
  2. What happens to the class widths as you drag to the right?

2.2.129

(a) Increases (b) Decreases

Question 2.267

earthquakes

130. Click on the Stem-and-leaf tab.

  1. How many stems are there?
  2. Without counting, how many leaves are there? How do we know this?

Question 2.268

earthquakes

131. Select Split Stems.

  1. Now how many stems are there?
  2. How many leaves are there?
  3. Which stem-and-leaf display is preferable for the Earthquakes data—regular or split stems? Why?

2.2.131

(a) 6 (b) 57 (c) Split stems; answers will vary

CONSTRUCT YOUR OWN DATA SETS

Question 2.269

132. Construct your own right-skewed data set of about 20 values. Just make up the data points, but be sure you know what the data represent (income, housing costs, etc.).

  1. Construct a stem-and-leaf display of your data set.
  2. Construct a dotplot of your data set.

Question 2.270

133. Construct your own symmetric data set of about 20 values. Just make up the data points, but be sure you know what the data represent (for example, runs in a baseball game, number of right answers on a quiz).

  1. Construct a stem-and-leaf display of your data set.
  2. Construct a dotplot of your data set.

2.2.133

Answers will vary.

WORKING WITH LARGE DATA SETS

image Petit larceny. Use the Petit Larceny data set for Exercises 134–141.

Question 2.271

petitlarceny

134. Build a frequency histogram of the number of petit larceny cases, per precinct, for 2000.

Question 2.272

petitlarceny

135. Build a relative frequency histogram of the number of petit larceny cases, per precinct, for 2000.

2.2.135

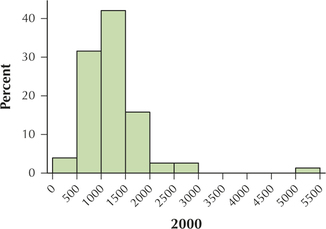
image

Question 2.273

petitlarceny

136. Build a histogram of the number of petit larceny cases, per precinct, for 2013. Make sure you use the same scale for the x axis and the y axis in each case, so that you may compare the two histograms more easily.

Question 2.274

petitlarceny

137. Compare the two histograms of petit larceny cases in 2000 and 2013. Describe any differences between the histograms. Would you say this reflects good news or bad news?

2.2.137

The number of petit larceny cases appears to be decreasing. This is good news.

Question 2.275

petitlarceny

138. Identify the precinct with the unusual number of petit larceny cases in each case. Using the Internet, research where this precinct lies in New York City.

Question 2.276

petitlarceny

139. Construct a comparison dotplot of the number of petit larcenies for the years 2000 and 2013. Describe any differences between the two groups.

2.2.139

image

The number of petit larcenies appears to be decreasing.

Question 2.277

petitlarceny

140. Build stem-and-leaf displays of the number of petit larcenies for the years 2000 and 2013. Describe any difference between the two groups.

Question 2.278

petitlarceny

141. Which graph—the histogram, the dotplot, or the stem-and-leaf display—is preferable if your objective is to:

  1. assess symmetry and skewness?
  2. be able to construct it quickly using paper and pencil?
  3. retain complete knowledge of the original data set?
  4. give a presentation to people who have never taken a stats course?

2.2.141

Dotplot Histogram Stem-and-leaf
(a) Symmetry and skewness Appropriate to use for small ranges of data Appropriate to use Appropriate to use for small ranges of data
(b) Construct using pencil and paper Easily done for small ranges of data Easily done for small ranges of data Easily done for small ranges of data
(c) Retain complete knowledge of the data Appropriate Appropriate only if the data are ungrouped Appropriate
(d) Presentation in front of non-statisticians Appropriate Appropriate Appropriate