7.2 Section 7.1 Exercises

CLARIFYING THE CONCEPTS

Question 7.1

1. Explain what a sampling distribution is. Why are sampling distributions so important? (p. 396)

7.1.1

It consists of the sample statistics of all possible samples of size from the population. Sampling distributions can tell us about the expected location and variability of a statistic.

Question 7.2

2. For a normal population, what can we say about the sampling distribution of the sample mean? (p. 399)

Question 7.3

3. True or false: and regardless of whether or not the sampling distribution of is normal. (pp. 397, 398)

7.1.3

True

Question 7.4

4. Use the Central Limit Theorem to explain what happens to the sampling distribution of as the sample size gets larger. (p. 401)

Question 7.5

5. According to our rule of thumb, what is the minimum sample size for approximate normality of the sampling distribution of ? (p. 401)

7.1.5

Question 7.6

6. State the three possible cases for the sampling distribution of . (p. 401)

Question 7.7

7. Suppose we want to decrease the size of the standard error to half its original size. How much do we have to increase the sample size? (p. 398)

7.1.7

4 times as large

Question 7.8

8. State the conditions when the sampling distribution of is neither normal nor approximately normal. (p. 401)

PRACTICING THE TECHNIQUES

image CHECK IT OUT!

To do Check out Topic
Exercises 9–16 Examples 1
and 2 		Mean, standard deviation,
and shape of the sampling
distribution of
Exercises 17–26 Example 4 Is the sampling
distribution of normal?
Exercises 27–32 Example 5 Finding probabilities for
the sample mean
Exercises 33–58 Example 6 Finding a value of , given
a probability or area
Exercises 59–70 Example 7 Finding probabilities
using the Central Limit
Theorem for Means
Exercises 71–80 Example 8 Finding two symmetric
sample mean values using
the Central Limit
Theorem for Means
Exercises 81–90 Examples 4,
6, and 8 		When appropriate,
calculating two symmetric
sample mean values

410

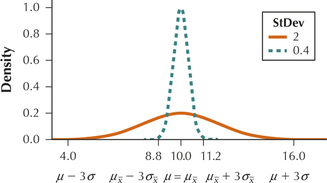
For Exercises 9–16, the characteristics of a normal distribution are given, along with a sample size for random samples taken from this distribution. Do the following:

  1. State the value of the mean of the sampling distribution of , that is, .
  2. Calculate the value of the standard error of the sampling distribution of , that is, .
  3. Draw a graph of the distribution curve of , similar to the orange curve in Figure 2 on page 398. On the number line, indicate and .
  4. Draw a graph of the distribution curve for the sampling distribution of , similar to the green curve in Figure 2 on page 398. On the number line, indicate , and . Note how both graphs are centered at the population mean, but also note that the variability of the sampling distribution of is less than that of the original distribution of .

Question 7.9

9.

7.1.9

(a) 10 (b) 0.4

(c) and (d)

image

Question 7.10

10.

Question 7.11

11.

7.1.11

(a) 0 (b) 0.3333

(c) and (d)

image

Question 7.12

12.

Question 7.13

13.

7.1.13

(a) 100 (b) 1

(c) and (d)

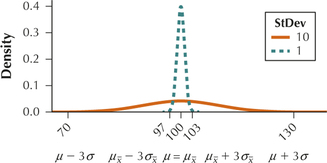
image

Question 7.14

14.

Question 7.15

15.

7.1.15

(a) 75 (b) 2.5

(c) and (d)

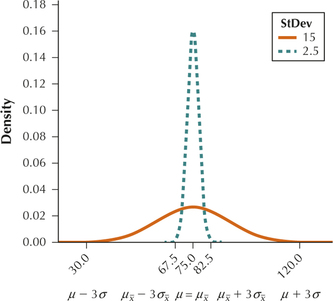
image

Question 7.16

16.

For Exercises 17–26, determine whether the sampling distribution of is normal, approximately normal, or unknown. (Hint: Use the Three Cases on page 401.)

Question 7.17

17. Systolic blood pressure readings are not normally distributed, with and . A random sample of size is taken.

7.1.17

Approximately normal

Question 7.18

18. Systolic blood pressure readings are not normally distributed, with and . A random sample of size is taken.

Question 7.19

19. The gas mileage for a 2014 Toyota Prius hybrid vehicle is not normally distributed, with miles per gallon and . A random sample of size is taken.

7.1.19

Unknown

Question 7.20

20. The gas mileage for a 2014 Toyota Prius hybrid vehicle is not normally distributed, with miles per gallon and . A random sample of size is taken.

Question 7.21

21. The pollen count distribution for Los Angeles in September is not normally distributed, with and . A random sample of size 16 is taken.

7.1.21

Unknown

Question 7.22

22. The pollen count distribution for Los Angeles in September is not normally distributed, with and . A random sample of size 64 is taken.

Question 7.23

23. Prices for boned trout are normally distributed, with per pound and . A random sample of size 16 is taken.

7.1.23

Normal

Question 7.24

24. Prices for boned trout are not normally distributed, with per pound and . A random sample of size 36 is taken.

Question 7.25

25. Accountant incomes are not normally distributed, with per year and . A random sample of 10 is taken.

7.1.25

Unknown

Question 7.26

26. Accountant incomes are not normally distributed, with per year and . A random sample of 100 is taken.

For Exercises 27–32, assume that test scores follow a normal distribution, with mean and standard deviation . Suppose we take random samples of size .

Question 7.27

27. Calculate and .

7.1.27

Question 7.28

28. Draw a graph of the sampling distribution of . On the number line, indicate , and .

Question 7.29

29. In your graph, shade the area to the left of 97. Find the probability that is less than 97.

7.1.29

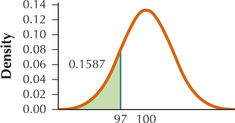
image

0.1587

Question 7.30

30. In your graph of the sampling distribution of , shade the area to the left of 98. Is this area smaller or larger than the area in the previous exercise? Will the probability that is less than 98 be greater than or less than the probability that is less than 97? Calculate the probability that is less than 98. Does this confirm your prediction?

Question 7.31

31. Without using your calculator, and referring to the previous exercise, use the symmetry of the normal distribution to calculate the probability that is greater than 102.

7.1.31

0.2525

Question 7.32

32. Without using your calculator, use your answers from Exercises 30 and 31 to compute the probability that lies between 98 and 102.

For Exercises 33–38, assume that the random variable is normally distributed, with mean and standard deviation . We take random samples of size .

Question 7.33

33. Calculate and .

7.1.33

Question 7.34

34. Draw a graph of the sampling distribution of . On the number line, indicate , and .

Question 7.35

35. In your graph, shade the area to the right of 0.2. Find the probability that is greater than 0.2.

7.1.35

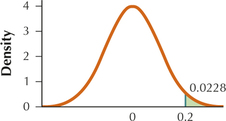
image

0.0228

Question 7.36

36. Calculate the probability that exceeds 0.1.

Question 7.37

37. Without using your calculator, and referring to the previous exercise, use the symmetry of the normal distribution to calculate the probability that is less than –0.1.

7.1.37

0.1587

Question 7.38

38. Without using your calculator, use your answers from Exercises 36 and 37 to compute the probability that lies between –0.1 and 0.1.

For Exercises 39–46, let the random variable be normally distributed, with mean and standard deviation . Suppose we take random samples of size . For Exercises 41–46, find the indicated values of :

Question 7.39

39. Calculate and .

7.1.39

Question 7.40

40. Draw a graph of the sampling distribution of . On the number line, indicate , and .

Question 7.41

41. The value of greater than 95% of values of

7.1.41

11.65

Question 7.42

42. The value of smaller than 95% of values of

Question 7.43

43. The 97.5th percentile of the sample means

7.1.43

11.96

Question 7.44

44. The 2.5th percentile of the sample means

Question 7.45

45. The two symmetric values for the sample mean that contain the middle 90% of sample means. (Hint: Use your answers to Exercises 41 and 42.)

7.1.45

8.35 and 11.65

Question 7.46

46. The two symmetric values for that contain the middle 95% of values. (Hint: Use your answers to Exercises 43 and 44.)

411

For Exercises 47–52, assume that the random variable follows a normal distribution, with mean and standard deviation . We take random samples of size .

Question 7.47

47. Calculate and .

7.1.47

Question 7.48

48. Draw a graph of the sampling distribution of . On the number line, indicate , and .

Question 7.49

49. Find the value of that is greater than 95% of all values of .

7.1.49

104.95

Question 7.50

50. Without using your calculator, use the symmetry of the normal distribution to calculate the value of that is smaller than 95% of all values of .

Question 7.51

51. In your graph, shade the middle 90% of the area under the curve. What are the two symmetric values for the sample mean that contain the middle 90% of sample means?

7.1.51

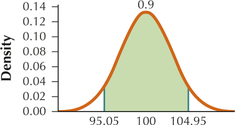
image

95.05 and 104.95

Question 7.52

52. What proportion of values lies outside the values you found in the previous exercise?

For Exercises 53–58, assume that the random variable is normally distributed, with mean and standard deviation . Suppose we take random samples of size .

Question 7.53

53. Calculate and .

7.1.53

Question 7.54

54. Draw a graph of the sampling distribution of . On the number line, indicate , and .

Question 7.55

55. Find the value of that is greater than 97.5% of all values of .

7.1.55

0.49

Question 7.56

56. Without using your calculator, use the symmetry of the normal distribution to calculate the value of that is smaller than 97.5% of all values of .

Question 7.57

57. In your graph, shade the middle 95% of the area under the curve. What are the two symmetric values for the sample mean that contain the middle 95% of sample means?

7.1.57

image

20.49 and 0.49

Question 7.58

58. What proportion of values lies outside the values you found in the previous exercise?

For Exercises 59–64, assume that is not normally distributed with mean and standard deviation . Suppose we take random samples of size .

Question 7.59

59. Calculate and .

7.1.59

Question 7.60

60. Draw a graph of the sampling distribution of . On the number line, indicate , and .

Question 7.61

61. In your graph, shade the area to the right of 2.6. Find the probability that is greater than 2.6.

7.1.61

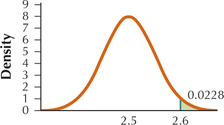
image

0.0228

Question 7.62

62. Calculate the probability that exceeds 2.75.

Question 7.63

63. In your graph, shade the area to the left of 2.4. Compute the probability that is less than 2.4.

7.1.63

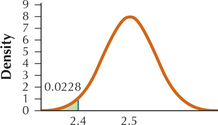
image

0.0228

Question 7.64

64. Now shade the area between 2.4 and 2.6. Calculate the probability that lies between 2.4 and 2.6.

For Exercises 65–70, is not normally distributed with mean and standard deviation . Suppose we take random samples of size .

Question 7.65

65. Calculate and .

7.1.65

Question 7.66

66. Draw a graph of the sampling distribution of . On the number line, indicate , and .

Question 7.67

67. In your graph, shade the area to the right of . Find the probability that is greater than .

7.1.67

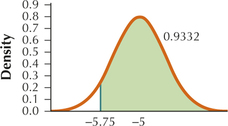
image

0.9332

Question 7.68

68. In your graph, shade the area to the left of . Calculate the probability that is less than .

Question 7.69

69. Shade the area between and . Would you say that this represents a large probability or a small probability?

7.1.69

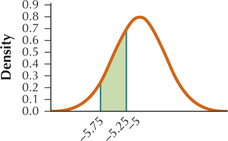
image

Question 7.70

70. Calculate the probability that the sample mean golf score lies between and .

For Exercises 71–76, has a mean and standard deviation . We take random samples of size .

Question 7.71

71. Calculate and .

7.1.71

Question 7.72

72. Draw a graph of the sampling distribution of . On the number line, indicate , and .

Question 7.73

73. Find the value of that is greater than 99.5% of all values of .

7.1.73

82.58

Question 7.74

74. Without using your calculator, use the symmetry of the normal distribution to calculate the value of that is smaller than 99.5% of all values of .

Question 7.75

75. In your graph, shade the middle 99% of the area under the curve. What are the two symmetric values for the sample mean that contain the middle 99% of sample means?

7.1.75

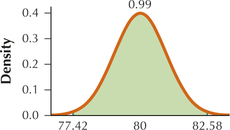
image

77.42 and 82.58

Question 7.76

76. What proportion of values lies outside the values you found in the previous exercise?

For Exercises 77–80, has a mean and standard deviation . Suppose we take random samples of size .

Question 7.77

77. Calculate and .

7.1.77

Question 7.78

78. Draw a graph of the sampling distribution of . On the number line, indicate , and .

Question 7.79

79. In your graph, shade the middle 95% of the area under the curve. What are the two symmetric values for the sample mean that contain the middle 95% of sample means?

7.1.79

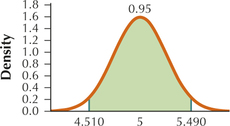
image

4.51 and 5.49

Question 7.80

80. What proportion of values lies outside the values you found in the previous exercise?

For the situations in Exercises 81–90, if possible, find the indicated two symmetric values of that contain the middle 95% of sample means. If not possible, explain why not.

Question 7.81

81. The pollen count distribution for Los Angeles in September is not normally distributed, with and . Random samples of size are taken.

7.1.81

Not possible; variable not normally distributed and sample size less than 30

Question 7.82

82. The pollen count distribution for Los Angeles in September is not normally distributed, with and . Random samples of size are taken.

Question 7.83

83. Prices for boned trout are normally distributed, with per pound and . Random samples of size are taken.

7.1.83

$3.755 and $4.245

Question 7.84

84. Prices for boned trout are not normally distributed, with per pound and . Random samples of size are taken.

Question 7.85

85. Accountant incomes are not normally distributed, with per year and . Random samples of size are taken.

7.1.85

Not possible; variable not normally distributed and sample size less than 30

Question 7.86

86. Accountant incomes are normally distributed, with per year and . Random samples of size are taken.

412

Question 7.87

87. Systolic blood pressure readings are not normally distributed, with and . Random samples of size are taken.

7.1.87

76.04 and 79.96

Question 7.88

88. Systolic blood pressure readings are not normally distributed, with and . Random samples of size are taken.

Question 7.89

89. The gas mileage for a 2014 Toyota Prius hybrid vehicle is not normally distributed, with miles per gallon and . Random samples of size are taken.

7.1.89

Not possible; variable not normally distributed and sample size less than 30

Question 7.90

90. The gas mileage for a 2014 Toyota Prius hybrid vehicle is not normally distributed, with miles per gallon and . Random samples of size are taken.

APPLYING THE CONCEPTS

Question 7.91

91. Blood Lead Contamination. A study2 of workers in lead-exposed jobs found that the mean blood lead level was micrograms, with a standard deviation of micrograms. Let the sample size be . Assume the distribution is normal.

  1. Find the mean of the sampling distribution and the standard error .
  2. Calculate the probability that the sample mean blood lead level will be less than 27.85 micrograms.
  3. Compute .

7.1.91

(a) micrograms, micrograms (b) 0.1587

(c) 0.0228

Question 7.92

92. Student Debt. The Project on Student Debt published a study3 in which they found that the mean amount of student debt owed by American college students was . Assume a standard deviation of . Suppose we take a sample of students. Assume the distribution is normal.

  1. Find the mean of the sampling distribution and the standard error .
  2. Calculate the probability that the sample mean student debt will be greater than $32,400.
  3. Compute .

Question 7.93

93. Measuring Well-Being. The Gallup-Healthways Well-Being Index represents an average of the reported emotional health, physical health, healthy behavior, and work environment of the survey respondents.4 Gallup reported that the mean Well-Being Index in 2013 was . Assume the standard deviation was . Suppose we take a sample of 25 survey respondents. If we assume the underlying distribution is normal, find the probability that the sample mean Well-Being Index will have the following values:

  1. Greater than 76.2
  2. Between 56.2 and 76.2
  3. Less than 56.2

7.1.93

(a) Approximately 0 (b) Approximately 1 (c) Approximately 0

Question 7.94

94. Statisticians' Salaries. If you enjoy statistics, you may want to become a statistician. The U.S. Census Bureau reported in 2014 that the median salary for mathematicians and statisticians was about $86,000. Income data is usually right-skewed, so we may safely assume that the mean is higher. Suppose the salaries of statisticians have a mean of and a standard deviation of .

Suppose we take samples of size 100 statisticians. Find the probability that the sample mean salary will have the following values:

  1. More than $106,000
  2. Less than $90,000
  3. Between $90,000 and $106,000

Question 7.95

95. Blood Lead Contamination. Refer to Exercise 91.

  1. Find the sample mean blood lead level greater than 95% of all sample mean blood lead levels.
  2. Find the value of smaller than 95% of all sample mean blood lead levels.
  3. What are the two symmetric values of that contain the middle 90% of sample means?

7.1.95

(a) 37.2575 micrograms (b) 25.5425 micrograms (c) 25.5425 micrograms and 37.2575 micrograms

Question 7.96

96. Student Debt. Refer to Exercise 92.

  1. Find the sample mean student debt greater than 97.5% of all sample mean student debts.
  2. Find the value of smaller than 97.5% of all sample mean student debts.
  3. What are the two symmetric values of that contain the middle 95% of sample means?

Question 7.97

97. Measuring Well-Being. Refer to Exercise 93.

  1. What are the two symmetric values of that contain the middle 99% of sample means?
  2. Draw a graph of the sampling distribution of , showing , along with the two symmetric values of from part (a). Shade the area under the curve between these two values of , and indicate the amount of area this represents.

7.1.97

(a) 61.05 and 71.35

(b)

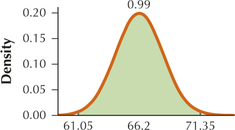
image

Question 7.98

98. Statisticians' Salaries. Refer to Exercise 94.

  1. What are the two symmetric values of that contain the middle 80% of sample means?
  2. Draw a graph of the sampling distribution of , showing , along with the two symmetric values of from part (a). Shade the area under the curve between these two values of , and indicate the amount of area this represents.

Question 7.99

99. Cholesterol Levels. The Centers for Disease Control and Prevention reports that the mean serum cholesterol level in Americans is 202. Assume that the standard deviation is 45. There is no information about the distribution. We take a sample of 36 Americans.

  1. Find .
  2. Calculate .

7.1.99

(a) 0.0918 (TI-83/84: 0.0912) (b) 0.8164 (TI-83/84: 0.8176)

Question 7.100

100. Tennessee Temperatures. According to the National Oceanic and Atmospheric Administration, the mean temperature for Nashville, Tennessee, in the month of January between 1872 and 2014 was 38.6°F. Assume that the standard deviation is 10°F, but the distribution is unknown. If we take a sample of , find the following probabilities:

Question 7.101

101. Computers per School. The National Center for Educational Statistics (http://nces.ed.gov) reported that the mean number of instructional computers per public school nationwide was 124. Assume that the standard deviation is 50 computers and no information is available about the shape of the distribution. Suppose we take a sample of size 100 public schools. Compute the following probabilities:

7.1.101

(a) 0.0026 (b) 0.4974

413

Question 7.102

102. Cholesterol Levels. Refer to Exercise 99.

  1. Find the sample mean serum cholesterol level that is larger than 95% of all such sample means.
  2. Calculate the sample mean serum cholesterol level that is smaller than 95% of all such sample means.

Question 7.103

103. Tennessee Temperatures. Refer to Exercise 100.

  1. Find the sample mean temperature that is larger than 97.5% of all such sample means.
  2. Calculate the sample mean temperature that is smaller than 97.5% of all such sample means.
  3. Draw a graph of the sampling distribution of . Indicate , the two values from (a) and (b), and the area between them.

7.1.103

(a) 41.87 (b) 35.33

(c)

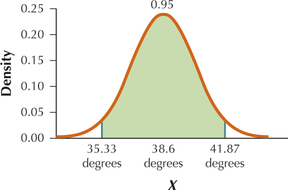
image

Question 7.104

104. Computers per School. Refer to Exercise 101.

  1. Find the 0.5th percentile of sample mean numbers of computers.
  2. Compute the 99.5th percentile of sample mean numbers of computers.
  3. Draw a graph of the sampling distribution of . Indicate , the two values from (a) and (b), and the area between them.

Question 7.105

105. Carbon Dioxide Concentration. The Carbon Dioxide Information Analysis Center (cdiac.ornl.gov/pns/current_ghg.html) reported in 2014 that the mean concentration of the greenhouse gas carbon dioxide is 397 parts per million (ppm). Suppose the population is normally distributed, assume that the standard deviation is 25 ppm, and suppose we take atmospheric samples from 25 cities.

  1. Calculate the probability that the sample mean carbon dioxide concentration will be between 387 and 407 ppm.
  2. Which sample mean represents the median sample mean? Explain how you know this.
  3. Find the two symmetric sample mean carbon dioxide concentrations containing the middle 99% of all sample means.

7.1.105

(a) 0.9544 (b) 397 ppm; in a normal distribution the median equals the mean. (c) 384.12 ppm and 409.88 ppm

Question 7.106

106. Short-Term Memory. In a famous research paper in the psychology literature, George Miller found that the amount of information humans could process in short-term memory was 7 bits (pieces of information), plus or minus 2 bits.5 Assume that the mean number of bits is 7 and the standard deviation is 2, and that the distribution is normal. Suppose we take a sample of 100 people and test their short-term memory skills.

  1. Find the probability that the sample mean number of bits retained in short-term memory lies between 6.8 and 7.2.
  2. Between which two values do the middle 95% of sample mean number of bits retained in short-term memory lie?

Blood Glucose Levels. Use the following information for Exercises 107–109. The population mean blood glucose levels is with standard deviation . Here is the normal probability plot for the population of patients.

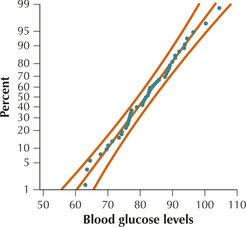
image
Normal probability plot of blood glucose levels.

Question 7.107

107. Does the normal probability plot show evidence in favor of normality or against normality? What characteristics of the plot illustrate this evidence?

7.1.107

In favor of normality. All of the points are between the curved lines and most of the points are close to the center line.

Question 7.108

108. If possible, find the probability that a random sample of patients will have a mean blood glucose level greater than 86. If not possible, explain why not.

Question 7.109

109. If possible, find the probability that a random sample of patients will have a mean blood glucose level greater than 86. If not possible, explain why not.

7.1.109

0 (TI-83/84: 0.0001591)

Adjusted Gross Income. Use the following information for Exercises 110–113. The population mean adjusted gross income for instructors at a certain college is with standard deviation . Here is the normal probability plot for the population of instructors.

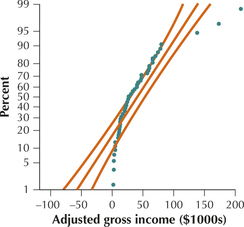
image
Normal probability plot of adjusted gross income.

Question 7.110

110. Does the normal probability plot show evidence in favor of normality or against normality? What characteristics of the plot illustrate this evidence?

Question 7.111

111. If possible, find the probability that a random sample of instructors will have a mean adjusted gross income between $40,000 and $60,000. If not possible, explain why not.

7.1.111

Not possible. The variable is not normally distributed and the sample size is less than 30.

414

Question 7.112

112. If possible, find the probability that a random sample of instructors will have a mean adjusted gross income between $40,000 and $60,000. If not possible, explain why not.

Question 7.113

image 113. Refer to Exercise 112. What if the sample size used was some unspecified value greater than 36? Describe how and why this change would have affected the following, if at all. Would the quantities increase, decrease, remain unchanged? Or is there insufficient information to tell what would happen? Explain your answers.

7.1.113

(a) Remain unchanged. From Fact 1 in Section 7.1, . Thus does not depend on the sample size . (b) Decrease. Since , an increase in the sample size results in a decrease in . (c) Insufficient information to tell. If , then . Since decreases and is positive, will increase. If , then . Thus will remain 0. If , then . Since decreases and is positive, will decrease. (d) Increase. From part (c), will increase and will decrease. Thus the area between these two values will increase. Since is the area between these two values of will increase.

image Chapter 7 Case Study: Trial of the Pyx. Refer to the Case Study on pages 407, 408, and 409 for Exercises 114, 115, 116, 117, and 118.

Question 7.114

114. What were the chances that the Master of the Mint would have been accused of cheating if he had in fact been completely honest?

In the Case Study, we interpreted the phrase “much less than” to mean a measurement that is 2 or more standard deviations below the mean. For Exercises 115–118, suppose we interpret the phrase “much less than” to mean a measurement that is 3 or more standard deviations below the mean.

Question 7.115

115. Use the methods shown in the Case Study to answer the following questions:

  1. What would be the new value of ?
  2. What would be the standard deviation s for each gold piece?
  3. By the Empirical Rule, about what proportion of the mean weights would you now expect to lie between 127.68 and 128.32?

7.1.115

(a) 0.1067 gram (b) 1.067 grams (c) About 0.997

Question 7.116

116. Assume “just a little debasement” from 128 grams per coin to 127.9 grams per coin.

  1. Find .
  2. What is the probability that the Master of the Mint would get away with just this little debasement? That he would get caught?
  3. Compare the probabilities in (b) with those in the Case Study in the text. Which values favor the Master of the Mint?

Question 7.117

117. Assume that greed attacked the Master of the Mint and he went for the big debasement from 128 grams per coin to 127.3 grams per coin.

  1. Find .
  2. What is the probability that the Master of the Mint would get away with this big debasement? That he would get caught?
  3. Compare the probabilities in (b) with those in the Case Study in the text. Which values favor the Master of the Mint?

7.1.117

(a) 0.0002 (b) 0.0002, 0.9998 (c) The value found in the original case study in the text favors the Master of the Mint.

Question 7.118

118. The Master of the Mint wanted to choose a mean value so that his chances of failing the Trial of the Pyx were 25%. Which mean value is this?

Use the Central Limit Theorem applet for Exercises 119 and 120.

Question 7.119

119. Describe the shape of the sampling distribution of for the following sample sizes:

  1. 2
  2. 5
  3. 30

7.1.119

(a)

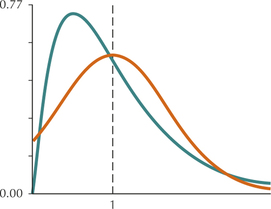
image

(b)

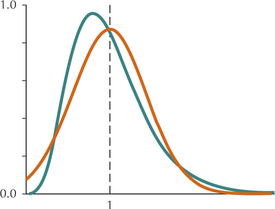
image

(c)

image

Question 7.120

120. At what sample size would you say the sampling distribution of becomes approximately normal?

BRINGING IT ALL TOGETHER

SAT Math Scores. Use this information for Exercises 121–126. The College Board (www.collegeboard.com) reports that the nationwide mean math SAT score for 2013 is 514. Assume that the standard deviation is 116 and that the scores are normally distributed.

Question 7.121

121. What is the probability that a randomly selected SAT Math score will be less than 500?

7.1.121

0.4522

Question 7.122

122. As a researcher, you are looking at samples of SAT Math scores of size 16.

  1. Find .
  2. Find .
  3. What can you say about the sampling distribution of the sample mean? How do you know this?

Question 7.123

123. Refer to Exercise 122.

  1. What is the probability that a sample of 16 students will have a sample mean math SAT score below 500?
  2. Why is the probability so much lower for the sample mean than for a particular student?

7.1.123

(a) 0.3156 (b) Means are less variable than individual values.

Question 7.124

124. Calculate the following sample mean values:

  1. 99.5th percentile of the sample mean SAT Math scores
  2. 0.5th percentile of the sample mean SAT Math scores

Question 7.125

image 125. Refer to Exercise 123. What if the population standard deviation was greater than 116? Explain how this would affect the following, if at all:

  1. Probability that a randomly selected SAT Math score will be less than 500
  4. Sampling distribution of the sample mean

7.1.125

(a) Increase (b) Remain the same (c) Increase (d) Still normal with but would increase

Question 7.126

image 126. What if the population standard deviation was greater than 116? Explain how this would affect the following, if at all:

  1. Probability that a sample of 16 SAT Math scores will have a mean less than 500
  2. 99.5th percentile of the sample mean SAT Math scores
  3. 0.5th percentile of the sample mean SAT Math scores