8.2 Infinite SeriesPrinted Page 553
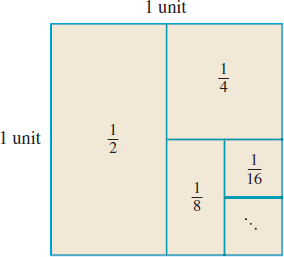
Is it possible for the sum of an infinite collection of nonzero numbers to be finite? Look at Figure 17. The square in the figure has sides of length 1 unit, making its area 1 square unit. If we divide the square into two rectangles of equal area, each rectangle has an area of 12 square unit. If one of these rectangles is divided in half, the result is one rectangle of area 12 square unit and two squares, the area of each equaling 14 square unit. If we were to continue the process of dividing one of the smallest regions in half, we would obtain a decomposition of the original area of 1 square unit into rectangles of area 12, 14, 18, 116, and so forth. Therefore, \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ 1=\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{8}+\dfrac{1}{16}+\cdots }}
554
Surprised?
Now look at this result from a different point of view by starting with the infinite sum \begin{equation*} \dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{8}+\dfrac{1}{16}+\cdots \tag{1} \end{equation*}
One way we might add the fractions is by using partial sums to see whether a trend develops. The first five partial sums are \begin{eqnarray*} \dfrac{1}{2} &=& 0.5 \\ \dfrac{1}{2}+\dfrac{1}{4} &=& \dfrac{3}{4}=0.75 \\ \dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{8} &=& \dfrac{3}{4}+\dfrac{1}{8}=\dfrac{7}{8}=0.875 \\ \dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{8}+\dfrac{1}{16} &=& \dfrac{7}{8}+\dfrac{1}{16}=\dfrac{15}{16}=0.9375 \\ \dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{8}+\dfrac{1}{16}+\dfrac{1}{32} &=& \dfrac{15}{16}+\dfrac{1}{32}=\dfrac{31}{32}=0.96875 \end{eqnarray*}
Each of these sums uses more terms from (1), and each sum seems to be getting closer to 1. The infinite sum in (1) is an example of an infinite series.
DEFINITION Infinite Series
If a_{1}, a_{2}, \ldots , a_{n}, \ldots is an infinite collection of numbers, the expression \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{\sum\limits_{k\,=\,1}^{\infty}a_{k}=a_{1}+~a_{2}+ \cdots +~a_{n}+ \cdots }}
is called an infinite series or, simply, a series.
The numbers a_{1}, a_{2},\ldots , a_{n}, \ldots are called the terms of the series, and the number a_{n} is called the n th term or general term of the series. The symbol \sum stands for summation; k is the index of summation. Although the index of summation can begin at any integer, in most of our work with series, it will begin at 1.
NEED TO REVIEW?
Sums and summation notation are discussed in Appendix A.5, pp. A-40 to A-42.
1 Determine Whether a Series Has a SumPrinted Page 554
To define a sum of an infinite series \sum\limits_{k\,=\,1}^{\infty }a_{k}, we make use of the sequence \{S_{n}\} defined by \begin{array}{cl} S_{1} & =a_{1} \\ S_{2} & =a_{1}+~a_{2}= \sum\limits_{k\,=\,1}^{2}a_{k} \\ \vdots & \\ S_{n} & =a_{1}+~a_{2}+ \cdots +a_{n}=~\sum\limits_{k\,=\,1}^{n}a_{k} \\ \vdots & \end{array}
This sequence \{S_{n}\} is called the sequence of partial sums of the series \sum\limits_{k\,=\,1}^{\infty }a_{k}.
For example, consider again the series \sum_{k\,=\,1}^{\infty }\frac{1}{2^{k}}=\frac{1}{2} +\frac{1}{2^{2}}+\frac{1 }{2^{3}}+\frac{1}{2^{4}}+\cdots =\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1 }{16}+\cdots
555
As it turns out, the partial sums S_{n} can each be written as 1 minus a power of \dfrac{1}{2}, as follows: \begin{array}{cll} S_{1} &=& a_{1}=\dfrac{1}{2}=1-\dfrac{1}{2} \\[8pt] S_{2} &=& S_{1}+a_{2}=\left( 1-\dfrac{1}{2}\right) +\dfrac{1}{4}=1-\dfrac{1}{4}=1-\dfrac{1}{2^{2}} \\[10pt] S_{3} &=& S_{2}+a_{3}=\left( 1-\dfrac{1}{4}\right) +\dfrac{1}{8}=1-\dfrac{1}{8}=1-\dfrac{1}{2^{3}} \\[10pt] S_{4} &=& S_{3}+a_{4}=\left( 1-\dfrac{1}{8}\right) +\dfrac{1}{16}=1-\dfrac{1}{16}=1-\dfrac{1}{2^{4}} \\[3pt] & &\vdots \\[4pt] S_{n} &=& 1-\dfrac{1}{2^{n}} \\[3pt] & & \vdots \end{array}
The nth partial sum is S_{n}=1-\dfrac{1}{2^{n}}, and as n increases, the sequence \{S_{n}\} of partial sums approaches a limit. That is, \lim\limits_{n\rightarrow \infty }S_{n}=\lim\limits_{n\rightarrow \infty }\left( {1-\frac{1}{2^{n}}}\right) =\lim_{n\,\rightarrow \,\infty}1-\lim\limits_{n\rightarrow \infty }\,\frac{1}{2^{n}}=1-0=1
We agree to call this limit the sum of the series, and we write \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \sum\limits_{k\,=\,1}^{\infty}\dfrac{1}{2^{k}}=\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{8}+\dfrac{1}{16}+\cdots =1}}
DEFINITION Convergence, Divergence of an Infinite Series
If the sequence \{S_{n}\} of partial sums of an infinite series \sum\limits_{k\,=\,1}^{\infty }a_{k} has a limit S, then the series converges and is said to have the sum S. That is, if \lim\limits_{n\,\rightarrow \,\infty }S_{n}=S, then \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{\sum\limits_{k\,=\,1}^{\infty}a_{k}=a_{1}+ a_{2}+\cdots + a_{n}+\cdots =S }}
An infinite series diverges if the sequence of partial sums diverges.
EXAMPLE 1Finding the Sum of a Series
Show that \sum_{k\,=\,1}^{\infty }\frac{1}{k(k+1)}=\frac{1}{1\cdot 2}+\frac{1}{2\cdot 3 }+\frac{1}{3\cdot 4}+\cdots =\frac{1}{2}+\frac{1}{6}+\frac{1}{12}+\cdots =1
Solution We begin with the sequence \{S_{n}\} of partial sums, \begin{array}{cl} S_{1} &= \dfrac{1}{1\cdot 2} \\[10pt] S_{2} &= \dfrac{1}{1\cdot 2}+\dfrac{1}{2\cdot 3} \\[10pt] S_{3} &= \dfrac{1}{1\cdot 2}+\dfrac{1}{2\cdot 3}+\dfrac{1}{3\cdot 4} \\ \vdots & \\ S_{n} &= \dfrac{1}{1\cdot 2}+\dfrac{1}{2\cdot 3}+\dfrac{1}{3\cdot 4}+\cdots +\dfrac{1}{n(n+1)} \\ \vdots & \end{array}
556
Since \begin{array}{l@{\hspace{14.5pt}}l} \dfrac{1}{n(n+1)}=\dfrac{1}{n}-\dfrac{1}{n+1} & {\color{#0066A7}{{\hbox{Use partial fractions.}}}} \end{array}
S_{n} can be written as S_{n}=\left( {\frac{1}{1}-\frac{1}{2}}\right) +\left( {\frac{1}{2}-\frac{1}{3 }}\right) +\cdots +\left( {\frac{1}{n-1}-\frac{1}{n}}\right) +\left( {\frac{1 }{n}-\frac{1}{n+1}}\right)
After removing parentheses notice that all the terms except the first and last cancel, so that S_{n}=1-\frac{1}{n+1}
Then \lim_{n\rightarrow \infty }S_{n}=\lim_{n\rightarrow \infty }\left( {1-\frac{1 }{n+1}}\right) =1
The series \sum\limits_{k\,=\,1}^{\infty }\dfrac{1}{k(k+1)} converges, and its sum is 1.
NOTE
Sums for which the middle terms cancel, as in Example 1, are called telescopingsums.
NOW WORK
EXAMPLE 2Showing a Series Diverges
Show that the series \sum\limits_{k\,=\,1}^{\infty }(-1)^{k}=-1+1-1+\cdots diverges.
Solution The sequence \{S_{n}\} of partial sums for this series is \begin{array}{c@{}l} S_{1} &= -1 \\ S_{2} &= -1+1=0 \\ S_{3} &= -1+1-1=-1 \\ S_{4} &= -1+1-1+1=0 \\ \vdots & \\ S_{n} &= \left\{ \begin{array}{r@{\qquad}l@{\quad}l} -1 & \hbox{if} & n \hbox{ is odd} \\ 0 & \hbox{if} & n \hbox{ is even} \end{array} \right.\end{array}
Since \lim\limits_{n\rightarrow \infty }S_{n} does not exist, the sequence \{S_{n}\} of partial sums diverges. Therefore, the series diverges.
NOW WORK
EXAMPLE 3Determining Whether a Series Converges or Diverges
Determine whether the series \sum\limits_{k\,=\,1}^{\infty }k=1+2+3+\cdots converges or diverges.
Solution The sequence \{S_{n}\} of partial sums is \begin{array}{c@{}l} S_{1} & =1 \\ S_{2} & =1+2 \\ S_{3} & =1+2+3 \\ \vdots & \\ S_{n} & =1+2+3+\cdots +n \end{array}
557
To express S_{n} in a way that will make it easy to find \lim\limits_{n\,\rightarrow \,\infty }S_{n}, we use the formula for the sum of the first n integers: S_{n}=\sum\limits_{k=1}^{n}k=1+2+3+ \cdots +n=\dfrac{n(n+1) }{2}
Since \lim\limits_{n\,\rightarrow \,\infty }S_{n}=\lim\limits_{n\,\rightarrow \,\infty }\dfrac{n(n+1) }{2} =\infty , the sequence \{S_{n}\} of partial sums diverges. So, the series \sum\limits_{k\,=\,1}^{\infty }k diverges.
NOW WORK
2 Analyze a Geometric SeriesPrinted Page 557
Geometric series occur in a large variety of applications including biology, finance, and probability. They are also useful in analyzing other infinite series.
DEFINITION Geometric Series
A series of the form \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \sum\limits_{k\,=\,0}^{\infty}ar^{k}=\sum\limits_{k\,=\,1}^{\infty }ar^{k-1}=a+ar+ar^{2}+\cdots +ar^{n-1}+\cdots }}
where a\neq 0 is called a geometric series.
In a geometric series, the ratio r of any two consecutive terms is a fixed real number.
To investigate the conditions for convergence of a geometric series, we examine the nth partial sum: \begin{equation*} S_{n}=a+ar+ar^{2}+\cdots +ar^{n-1} \tag{1} \end{equation*}
If r=0, the nth partial sum is S_{n}=a and \lim\limits_{n\rightarrow \infty }S_{n}=a. The sequence of partial sums converges when r=0.
If r=1, the series becomes \sum\limits_{k\,=\,1}^{\infty }a=a+a+\cdots +a+\cdots , and the nth partial sum is S_{n}=a+a+\cdots +a=na
Since a\neq 0, \lim\limits_{n\rightarrow \infty }S_{n}=\infty or -\infty , so the sequence \{S_{n}\} of partial sums diverges when r=1.
If r=-1, the series is \sum\limits_{k\,=\,1}^{\infty }a(-1)^{k-1}=a-a+a-a+\cdots and the nth partial sum is S_{n}=\left\{ \begin{array}{l@{\qquad}ll} 0 & \hbox{ if } & n \hbox{ is even} \\ a & \hbox{ if} & n \hbox{ is odd} \end{array} \right.
Since a\neq 0, \lim\limits_{n\rightarrow \infty }S_{n} does not exist. The sequence \{S_{n}\} of partial sums diverges when r=-1.
Suppose r\neq 0, r\neq 1, and r\neq -1. Since r\neq 0, we multiply both sides of (1) by r to obtain rS_{n}=ar+ar^{2}+\cdots +ar^{n}
Now subtract rS_{n} from S_{n}. \begin{eqnarray*} S_{n}-rS_{n} &=& (a+ar+ar^{2}+\cdots +ar^{n-1})-(ar+ar^{2}+\cdots +ar^{n-1}+ar^{n})\\ &=& a-ar^{n} \\ S_{n}(1-r) &=& a(1-r^{n}) \end{eqnarray*}
558
Since r\neq 1, the nth partial sum of the geometric series can be expressed as S_{n}=\dfrac{a(1-r^{n})}{1-r}=\dfrac{a-ar^{n}}{1-r}=\dfrac{a}{1-r}-\dfrac{ ar^{n}}{1-r}\
Now, \lim\limits_{n\rightarrow \infty }S_{n}=\lim\limits_{n\rightarrow \infty }\left[ \frac{a}{1-r}-\frac{ar^{n}}{1-r}\right] =\lim\limits_{n\rightarrow \infty } \frac{a}{1-r}-\lim\limits_{n\rightarrow \infty }\frac{ar^{n}}{1-r}=\frac{a}{1-r} -\frac{a}{1-r}\lim\limits_{n\rightarrow \infty }r^{n}
We now use the fact that if \vert r\vert <1, then \lim\limits_{n\,\rightarrow \,\infty }\,r^{n}=0 (refer to page 546 in Section 8.1). We conclude that if \vert r\vert <1, then \lim\limits_{n\,\rightarrow \,\infty }S_{n}=\dfrac{a}{1-r}. So, a geometric series converges to S=\dfrac{a}{1-r} if -1<r<1.
If \vert r\vert >1, use the fact that \lim\limits_{x\, \rightarrow \,\infty }r^{n} does not exist to conclude that a geometric series diverges if r<-1 or r>1.
This proves the following theorem:
THEOREM Convergence of a Geometric Series
- If \vert r\vert <1, the geometric series \sum\limits_{k\,=\,1}^{\infty }ar^{k-1} converges, and its sum is \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{\sum\limits_{k\,=\,1}^{\infty }ar^{k-1}=\dfrac{a}{1-r}}}
- If \vert r\vert \geq 1, the geometric series \sum\limits_{k\,=\,1}^{\infty }ar^{k-1} diverges.
EXAMPLE 4Determining Whether a Geometric Series Converges
Determine whether each geometric series converges or diverges. If it converges, find its sum.
- (a) \sum\limits_{k\,=\,1}^{\infty }8 \left( \frac{2}{5}\right)^{k-1}
- (b) \sum\limits_{k\,=\,1}^{\infty }\left(-\frac{5}{9}\right) ^{k-1}
- (c) \sum\limits_{k\,=\,1}^{\infty }3 \left( \frac{3}{2}\right) ^{k-1}
- (d) \sum\limits_{k\,=\,1}^{\infty }\frac{1}{2^{k}}
- (e) \sum\limits_{k\,=\,0}^{\infty }\left( \frac{1}{3}\right) ^{k-1}
Solution We compare each series to \sum\limits_{k\,=\,1}^{\infty }ar^{k-1}.
(a) In this series a=8 and r=\dfrac{2}{5}. Since \vert r\vert=\dfrac{2}{5}<1, the series converges and \sum\limits_{k\,=\,1}^{\infty }8 \left( \frac{2}{5}\right) ^{k-1}=\frac{8}{1-\dfrac{2}{5}}=8 \left( \frac{5}{3}\right) =\frac{40}{3}
(b) Here, a=1 and r=-\dfrac{5}{9}. Since \vert r\vert =\dfrac{5}{9}<1, the series converges and \sum\limits_{k\,=\,1}^{\infty }\left( -\frac{5}{9}\right) ^{k-1}=\frac{1}{ 1-\left( -\dfrac{5}{9}\right) }=\frac{9}{14}
559
(c) Here, a=3 and r=\dfrac{3}{2}. Since \vert r\vert =\dfrac{3}{2}>1, the series \sum\limits_{k\,=\,1}^{\infty}3 \left( \dfrac{3}{2}\right) ^{k-1} diverges.
(d) \sum\limits_{k\,=\,1}^{\infty }\dfrac{1}{2^{k}} is not in the form \sum\limits_{k\,=\,1}^{\infty }ar^{k-1}. To place it in this form, we proceed as follows: \begin{eqnarray*} &\sum\limits_{k\,=\,1}^{\infty }~\frac{1}{2^{k}}=\sum\limits_{k\,=\,1}^{ \infty }\left( \frac{1}{2}\right) ^{k} = \sum\limits_{k\,=\,1}^{\infty }\left[ \dfrac{1}{2}\cdot \left( \dfrac{1}{2} \right) ^{k-1}\right] \\[-13pt] &\hspace{2pc} \underset{\color{#0066A7}{{{\hbox{Write in the form}}}} {\color{#0066A7}{\hbox{\(\sum\limits_{k=1}^{\infty}ar^{k-1}\)}}}}{\color{#0066A7}{{{\kern1pt\left\uparrow{\vphantom{\vrule width0pc height8pt depth0pt}}\right.}}}} \end{eqnarray*}
So, \sum\limits_{k\,=\,1}^{\infty }\dfrac{1}{2^{k}} is a geometric series with a=\dfrac{1}{2} and r=\dfrac{1}{2}. Since \vert r\vert <1, the series converges, and its sum is \sum\limits_{k\,=\,1}^{\infty }\frac{1}{2^{k}}=\frac{\dfrac{1}{2}}{1-\dfrac{ 1}{2}}=1
which agrees with the sum we found earlier.
(e) \sum\limits_{k\,=\,0}^{\infty }\left( \dfrac{1}{3}\right) ^{k-1} starts at 0, so it is not in the form, \sum\limits_{k\,=1}^{ \infty }ar^{k-1}. To place it in this form, change the index to l, where l=k+1. Then when k=0, l=1 and \sum\limits_{k\,=\,0}^{\infty }\left( \dfrac{1}{3}\right) ^{k-1} = \sum\limits_{l=1}^{\infty }\left(\dfrac{1}{3}\right) ^{l-2}=\sum\limits_{l=1}^{\infty }\left(\dfrac{1}{3}\right) ^{-1}\left( \dfrac{1}{3}\right) ^{l-1}=\sum\limits_{l=1}^{\infty }3 \left( \dfrac{1}{3} \right)^{l-1}
That is, \sum\limits_{k\,=\,0}^{\infty }\left( \dfrac{1}{3}\right) ^{k-1}=\sum\limits_{l=1}^{\infty }3 \left( \dfrac{1}{3}\right) ^{l-1} is a geometric series with a=3 and r=\dfrac{1}{3}. Since \vert r\vert <1, the series converges, and its sum is \sum\limits_{k\,=\,0}^{\infty }\left( \dfrac{1}{3}\right) ^{k-1}=\dfrac{3}{1-\dfrac{1}{3}}=\dfrac{9}{2}
NOW WORK
EXAMPLE 5Writing a Repeating Decimal as a Fraction
Express the repeating decimal 0.090909\ldots as a quotient of two integers.
Solution We write the infinite decimal 0.090909\ldots as an infinite series: \begin{eqnarray*} 0.090909\ldots &=& 0.09 + 0.0009+0.000009+0.00000009+\cdots \\ &=& \dfrac{9}{100}+\dfrac{9}{10000} +\dfrac{9}{1000000}+\cdots \\ &=& \dfrac{9}{100}\left( 1+\dfrac{1}{100}+\dfrac{1}{10000}+\dfrac{1}{1000000} +\cdots\right) \\ &=& \sum\limits_{k\,=\,1}^{\infty }\dfrac{9}{100}\left( \frac{1}{ 100}\right) ^{k-1} \end{eqnarray*}
560
This is a geometric series with a=\dfrac{9}{100} and r=\dfrac{1}{100}. Since \left\vert r\right\vert <1, the series converges and its sum is \sum\limits_{k\,=\,1}^{\infty }\dfrac{9}{100}\left( \frac{1}{100}\right) ^{k-1}=\frac{\dfrac{9}{100}}{1-\dfrac{1}{100}}=\frac{9}{99}=\frac{1}{11}
So, 0.090909\ldots \,=\dfrac{1}{11}.
NOW WORK
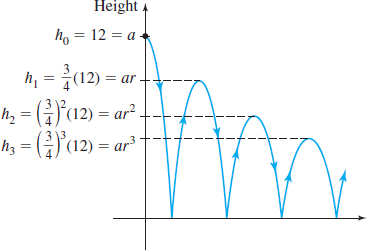
EXAMPLE 6Using a Geometric Series with a Bouncing Ball
A ball is dropped from a height of 12m. Each time it strikes the ground, it bounces back to a height three-fourths the distance from which it fell. Find the total distance traveled by the ball. See Figure 18.
Solution Let h_{n} denote the height of the ball on the nth bounce. Then \begin{array}{cl} h_{0} & =12 \\ h_{1} & =\dfrac{3}{4}(12) \\ h_{2} & =\dfrac{3}{4}\left[ \dfrac{3}{4}(12)\right] =\left( \dfrac{3}{4}\right) ^{2}(12) \\ \vdots & \\ h_{n} & =\left( \dfrac{3}{4}\right) ^{n}(12) \end{array}
After the first bounce, the ball travels up a distance h_{1}=\dfrac{3}{4}(12) and then the same distance back down. Between the first and the second bounce, the total distance traveled is therefore h_{1}+h_{1}=2h_{1}. The total distance H traveled by the ball is \begin{eqnarray*} H=h_{0}+2h_{1}+2h_{2}+2h_{3}+\cdots &=& h_{0}+\sum\limits_{k\,=\,1}^{\infty }\left( 2h_{k}\right) =12+\sum\limits_{k\,=\,1}^{\infty }2 \left[ 12 \left( { \frac{3}{4}}\right) ^{k}\right]\\[8pt] &=& 12+\sum\limits_{k\,=\,1}^{\infty }24\left[ \frac{3}{4}\left( {\frac{3}{4}}\right) ^{k-1}\right] \\ &=& 12+\sum\limits_{k\,=\,1}^{\infty }18\left( {\frac{3}{4}}\right) ^{k-1} \end{eqnarray*}
The sum is a geometric series with a=18 and r=\dfrac{3}{4}. The series converges and H=12+\sum\limits_{k\,=\,1}^{\infty }18\left( \frac{3}{4}\right) ^{k-1}=12 + \frac{18}{1-\dfrac{3}{4}}=84
The ball travels a total distance of 84 m.
NOW WORK
3 Analyze the Harmonic SeriesPrinted Page 561
561
Another useful series, even though it diverges, is the harmonic series.
DEFINITION Harmonic Series
The infinite series \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{\sum\limits_{k\,=\,1}^{\infty }\dfrac{1}{k}=1+ \dfrac{1}{2}+\dfrac{1}{3}+\cdots }}
is called the harmonic series.
THEOREM
The harmonic series \sum\limits_{k\,=\,1}^{\infty }\dfrac{1}{k} diverges.
RECALL
An unbounded sequence diverges (p. 547).
Proof
To show that the harmonic series diverges, we look at the partial sums whose indexes of summation are powers of 2. That is, we investigate the sequence S_{1}, S_{2}, S_{4}, S_{8}, and so on. We can show that this sequence is not bounded as follows: \begin{array}{l} S_{1}=1>\dfrac{1}{2}=1\left( \dfrac{1}{2}\right)\\[10pt] S_{2}=1+\dfrac{1}{2}>\dfrac{1}{2}+\dfrac{1}{2}=2\left( \dfrac{1}{2}\right)\\[10pt] S_{4}=1+\dfrac{1}{2}+\left( \dfrac{1}{3}+\dfrac{1}{4}\right) >2\left( \dfrac{ 1}{2}\right) +\left( \dfrac{1}{4}+\dfrac{1}{4}\right) =3\left( \dfrac{1}{2}\right)\\ S_{8}=1+\dfrac{1}{2}+\left( \dfrac{1}{3}+\dfrac{1}{4}\right) +\left( \dfrac{1}{5}+\dfrac{1}{6}+\dfrac{1}{7}+\dfrac{1}{8}\right)\\ \quad \, >3\left( \dfrac{1}{2}\right) +\left( \dfrac{1}{8}+\dfrac{1}{8}+\dfrac{1}{8}+\dfrac{1}{8}\right) =4\left( \dfrac{1}{2}\right)\\ \vdots \\ \hspace{-10pt} S_{2^{n-1}}>n\left( \dfrac{1}{2}\right) \end{array}
We conclude that the sequence \left\{ S_{2^{n-1}}\right\} is not bounded, so the sequence \{S_{n}\} of partial sums is not bounded. It follows that the sequence \{S_{n}\} of partial sums diverges. Therefore, the harmonic series \sum\limits_{k\,=\,1}^{\infty }\dfrac{1}{k} diverges.
Summary
- A series \sum\limits_{k\,=\,1}^{\infty }a_{k} converges if and only if its sequence \{S_{n}\} of partial sums converges.
- The geometric series \sum\limits_{k\,=\,1}^{\infty }ar^{k-1}, a\neq 0 , converges when \vert r\vert <1 and diverges for \vert r\vert \geq 1. If the geometric series converges, its sum is S=\dfrac{a}{1-r}.
- The harmonic series \sum\limits_{k\,=\,1}^{\infty }\dfrac{1}{k} diverges.
562
Using a Geometric Series in a Biology Application*
Children’s Hospital of Philadelphia (2009), Retinoblastoma, http://www.CHOP.edu. J. V. Neel & W. J. Schull (1958), Human heredity, 3rd ed. (pp. 333–334), Chicago: University of Chicago Press. Reprinted by permission.
This application deals with the rate of occurrence of retinoblastoma, a rare type of eye cancer in children. An allele (allelomorph) is a gene that gives rise to one of a pair of contrasting characteristics, such as smooth or rough, tall or short. Each person normally has two such genes for each characteristic. An individual may have two “tall” genes, two “short” genes, or one of each. In reproduction, each parent gives one of the two types to the child.
The tendency to develop retinoblastoma apparently depends on the mutation of both copies of a gene, called RB1. The mutation rate from a normal RB1 allele to the mutant RB1 in each generation is approximately m=0.00002=2\times 10^{-5}. In this example, we ignore the very unlikely possibility of mutation from an abnormal RB1 to a normal RB1 gene. At the beginning of the twentieth century, retinoblastoma was nearly always fatal, but by the early 1950s, approximately 70% of children affected with the disease survived, although they usually became blind in one or both eyes. The current (2009) survival rate is about 95% and the goals of treatment are to prevent the tumor cells from growing and spreading and to preserve vision.
Assume that survivors reproduce at about half the normal rate. (The assumption is based on scientific guesswork.) Then the productive proportion of persons affected with the retinoblastoma in 2009 was r=\left( 0.5\right) \left( 0.95\right) =0.475. This rate is remarkable, considering that in 1900, r\approx 0, and in 1950 r\approx 0.35.
Starting with zero inherited cases in an early generation, for the nth consecutive generation, we obtain a rate of \begin{array}[t]{l} m & {\hbox{due to mutation in the nth generation}} \\ mr & {\hbox{due to mutation in the (n-1)st generation}} \\ mr^{2} & {\hbox{due to mutation in the (n-2)nd generation}}\\ \hspace{-8pt}\vdots\hspace{8pt}\\ mr^{n} & {\hbox{due to mutation in the zero (original) generation}} \end{array}
Then, the total rate of occurrence of the disease in the nth generation is p_{n}=m+mr+\cdots +mr^{n}=\frac{m(1-r^{n+1})}{1-r}
from which p=\lim_{n\rightarrow \infty }p_{n}=\frac{m}{1-r}=\dfrac{2\times 10^{-5}}{1-0.475}=3.810\times 10^{-5}
indicating that the total rate of persons affected with the disease will be almost twice the mutation rate.
Notice that if r=0, as in 1900, then p=m=2\times 10^{-5}, and that if r=0.35, as in 1950, then p=3.08\times 10^{-5}. We see that with better medical care, retinoblastoma has become more frequent. As medical care improves, the rate of occurrence of the disease can be expected to become even greater. As Neel and Schull pointed out, with improved medical care, the frequency of an abnormal gene RB1 increases rapidly at first, then more slowly, until an equilibrium point is reached.
*Adapted from J. L. Young & M. A. Smith (1999), Retinoblastoma. In L. A. G. Ries, M. A. Smith, J. G. Gurney, M. Linet, T. Tamra, J. L. Young, & G. R. Bunin (Eds.), Cancer incidence and survival among children and adolescents: United States SEER Program, 1975–1995, NIH Pub. No. 99-4649, Bethesda, MD: National Cancer Institute.