9.3 Surface Area of a Solid of RevolutionPrinted Page 656
656
OBJECTIVES
When you finish this section, you should be able to:
In Chapter 6, we used a definite integral to find the volume of a solid of revolution. To obtain the solid of revolution, we revolved a region around an axis. Here, we are interested in finding the surface area of the solid of revolution. To obtain the surface, we revolve a smooth curve about an axis.
NOTE
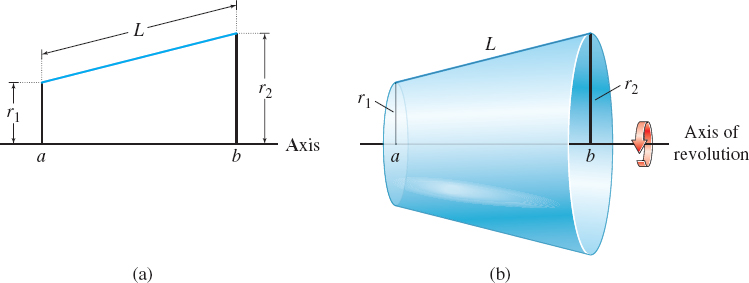
A frustum is a portion of a solid of revolution that lies between two parallel planes.
Consider a line segment of length L that lies above the x-axis. See Figure 19(a). If the region bounded by the line segment and the x-axis from a to b is revolved about an axis, the resulting solid of revolution is a frustum. The frustum of a right circular cone has slant height L and base radii r1 and r2. See Figure 19(b).
The surface area S of the frustum is \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ S=2\pi \left( \dfrac{r_{1}+r_{2}}{2}\right)\, L }}
That is, the surface area S equals the product of 2\pi , the average radius of the frustum, and the slant height of the frustum. This equation forms the basis for the formula for the surface area of a solid of revolution.
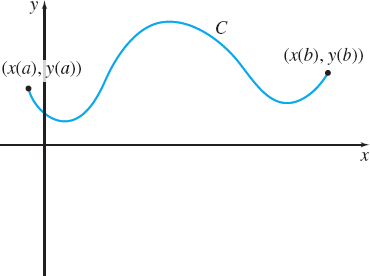
Suppose C is a smooth curve represented by the parametric equations \begin{equation*} x=x (t)\qquad y=y(t)\quad a\leq t\leq b \end{equation*}
where y=y(t)\geq 0 on the closed interval [a,b], as shown in Figure 20. Revolving C about the x-axis generates a solid of revolution with surface area S. To find S, we partition the interval [ a,b] into n subintervals: \begin{equation*} \lbrack a ,t_{1}], [t_{1},t_{2}], \ldots , [t_{i-1},t_{i}], \ldots , [t_{n-1},b] \end{equation*}
each of length \Delta t=\dfrac{b-a}{n}. Corresponding to each number a, t_{1}, t_{2}, \ldots , t_{i-1}, t_{i}, \ldots , t_{n-1}, b, there is a point P_{0}, P_{1}, \ldots , P_{i-1}, P_{i}, \ldots , P_{n-1}, P_{n} on the curve C. We join each point P_{i-1} to the next point P_{i} with a line segment and focus on the line segment joining the points P_{i-1} and P_{i}. See Figure 21(a). When this line segment of length d(P_{i-1},P_{i}) is revolved about the x-axis, it generates a frustum of a right circular cone whose surface area S_{i} is \begin{equation*} S_{i}=2\pi \left[ \frac{y(t_{i-1})+y(t_{i})}{2}\right] \, \left[d\,(P_{i-1},P_{i})\right] \tag{1} \end{equation*}
657
See Figure 21(b).
We follow the same reasoning used for finding the arc length of a smooth curve, (Section 9.2). Using the distance formula, the length of the ith line segment is \begin{equation*} d(P_{i-1},P_{i})= \sqrt{[ x(t_{i}) -x(t_{i-1}) ] ^{2}+[ y(t_{i}) -y(t_{i-1}) ] ^{2}} \end{equation*}
Now we apply the Mean Value Theorem to x(t) and y(t) . There are numbers u_{i} and v_{i} in each open interval ( t_{i-1},t_{i}) for which \begin{equation*} x(t_{i}) -x ( t_{i-1} ) =\left[ \dfrac{dx}{dt} (u_{i} ) \right] \, \Delta t\qquad\hbox{and}\qquad y(t_{i}) -y ( t_{i-1} ) =\left[ \dfrac{dy}{dt} ( v_{i} ) \right] \, \Delta t \end{equation*}
So, \begin{eqnarray*} d(P_{i-1},P_{i})&=& \sqrt{\left\{ \left[ \dfrac{dx}{dt}( u_{i}) \right] \, \Delta t\right\} ^{2}+ \left\{ \left[ \dfrac{dy}{dt}(v_{i}) \right] \, \Delta t\right\} ^{2}}\\[5pt] &=& \sqrt{\left[ \frac{dx}{dt}(u_{i})\right] ^{2}+ \left[ \frac{dy}{dt}(v_{i})\right] ^{2}}\,\Delta t \end{eqnarray*}
where u_{i} and v_{i} are numbers in the ith subinterval.
Now we replace d(P_{i-1},P_{i}) in equation (1) with \sqrt{\left[ \dfrac{dx}{dt}(u_{i})\right] ^{2}+\left[ \dfrac{dy}{dt}(v_{i})\right] ^{2}}\,\Delta t. Then the surface area generated by the sum of the line segments is \begin{equation*} \sum_{i=1}^{n}S_{i}=\sum_{i=1}^{n}2\pi \left[ \frac{y(t_{i-1})+y(t_{i})}{2} \right] \, \sqrt{\left[ \frac{dx}{dt}(u_{i})\right] ^{2}+\left[ \frac{dy}{dt} (v_{i})\right] ^{2}}\,\Delta t \end{equation*}
These sums approximate the surface area generated by revolving C about the x-axis and lead to the following result.
THEOREM Surface Area of a Solid of Revolution
The surface area S of a solid of revolution generated by revolving the smooth curve C represented by x=x(t),\;y=y(t),\;a\leq t\leq b, where y(t)\geq 0, about the x-axis is \begin{equation*} \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ S=2\pi \int_{a}^{b}y(t) \sqrt{\left( \dfrac{dx}{dt}\right) ^{2}+\left( \dfrac{dy}{dt}\right) ^{2}}\,dt }}\tag {2} \end{equation*}
1 Find the Surface Area of a Solid of Revolution Obtained from Parametric EquationsPrinted Page 659
658
EXAMPLE 1Finding the Surface Area of a Solid of Revolution Obtained from Parametric Equations
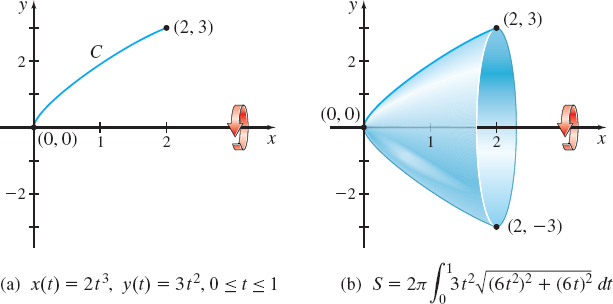
Find the surface area of the solid generated by revolving the smooth curve C represented by the parametric equations x(t) =2t^{3}, y(t) =3t^{2}, 0\leq t\leq 1, about the x-axis.
Solution We begin by graphing the smooth curve C and revolving it about the x-axis. See Figure 22.
We use formula (2) with \dfrac{dx}{dt}=\dfrac{d}{dt}\,\left( 2t^{3}\right) =6t^{2} and \dfrac{dy}{dt}=\dfrac{d}{dt}\,\left( 3t^{2}\right) =6t. Then \begin{eqnarray*} S &=&2\pi \int_{a}^{b}\,y(t) \, \sqrt{\left( \dfrac{dx}{dt}\right) ^{2}+\left( \dfrac{ dy}{dt}\right) ^{2}}\,dt=2\pi \int_{0}^{1}\,3t^{2}\,\sqrt{( 6t^{2})^{2}+( 6t) ^{2}}\,dt\\[5pt] &=&2\pi \int_{0}^{1}\,3t^{2}\,\sqrt{36t^{4}+36t^{2}}\,dt =36\pi \int_{0}^{1}\,t^{3}\,\sqrt{t^{2}+1}\,dt=\frac{36\pi }{2}\int_{1}^{2}\,(u-1)\sqrt{u}\,du\\[-10pt] &&\hspace{10.9pc}\underset{\underset{{{\color{#00ADEE}{{\hbox{when \(t=0, u=1;\) when \(t=1, u=2\)}}}}}}{\color{#00ADEE}{{{\hbox{\(u=t^{2}+1;\)}}} {\color{#00ADEE}{\hbox{\(du=2t dt\)}}}} \,} }{\color{#00ADEE}{{{\uparrow }}}}\\[-3pt] &=&18\pi\,\left[ \dfrac{2}{5}u^{5/2}-\frac{2}{3}u^{3/2}\right]_{1}^{2}=\frac{24\pi }{5}\,(\sqrt{2}+1) \end{eqnarray*}
The surface area of the solid of revolution is \dfrac{24\pi }{5}(\sqrt{2} +1)\approx 36.405 square units.
NOW WORK
To help remember the formula for the surface area of a solid of revolution, think of the integrand as the product of the slant height \sqrt{\left( \dfrac{dx}{dt}\right) ^{2}+\left( \dfrac{dy}{dt}\right) ^{2}} and the circumference 2\pi y of the circle traced by a point (x,y) on the corresponding sub-arc. Also keep in mind that the limits of integration are parameter values, not x values.
If the curve is revolved about the y-axis, we have a similar formula for the surface area of the solid of revolution.
THEOREM Surface Area of a Solid of Revolution
The surface area S of a solid of revolution generated by revolving the smooth curve C represented by x=x(t), y=y(t), a\leq t\leq b, where x=x(t)\geq 0, about the y-axis is \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ S=2\pi \int_{a}^{b} \, x(t) \sqrt{\left( \dfrac{dx}{dt}\right) ^{2}+\left( \dfrac{dy}{dt}\right) ^{2}}\,dt }}
2 Find the Surface Area of a Solid of Revolution Obtained from a Rectangular EquationPrinted Page 659
659
Let C be a smooth curve represented by a rectangular equation y=f(x), \ a\leq x\leq b, where f(x)\geq 0 on [a,b]. A set of parametric equations for this curve is x(t) =t and y(t) =f(t) . Then \dfrac{dx}{dt}=1, dx=dt, and \ \dfrac{dy}{dt}= \dfrac{dy}{dx}\dfrac{dx}{dt}=\dfrac{dy}{dx}\cdot 1=f’ ( x) . The surface area S of the solid of revolution obtained by revolving C, a\leq x\leq b , about the x-axis is S=2\pi \int_{a}^{b}\,y(t) \sqrt{\left( \dfrac{dx}{dt}\right) ^{2}+\left( \dfrac{dy}{dt}\right) ^{2}}\,dt. So in terms of y=f( x) , a\leq x\leq b, we have \begin{equation*} \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ S=2\pi \int_{a}^{b}\,f( x) \sqrt{1+[ f’ ( x) ] ^{2}}\,dx }} \tag{3} \end{equation*}
EXAMPLE 2Finding the Surface Area of a Solid of Revolution Obtained from a Rectangular Equation
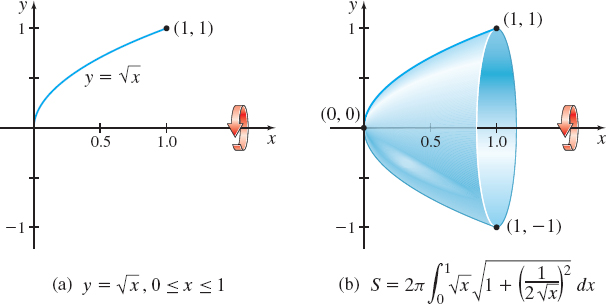
Find the surface area of the solid generated by revolving the curve represented by y= \sqrt{x}, from x=0 to x=1, about the x-axis.
Solution We begin with the graph of y=\sqrt{x} , 0\leq x\leq 1, and revolve it about the x-axis, as shown in Figure 23.
We use formula (3) with f( x) = \sqrt{x} and f’ ( x) =\dfrac{1}{2 \sqrt{x}}. The surface area S we seek is

The surface area of the solid of revolution is \dfrac{\pi }{6}(5 \sqrt{5} -1)\approx 5.330 square units.