Questions

Review Questions

1. What is meant by the luminosity of the Sun?

2. What is Kelvin-Helmholtz contraction? Why is it ruled out as a source of the present-day Sun’s energy?

3. Why is it impossible for the burning of substances like coal to be the source of the Sun’s energy?

4. What is hydrogen fusion? Why is hydrogen fusion fundamentally unlike the burning of a log in a fireplace?

5. If the electric force between protons were somehow made stronger, what effect would this have on the temperature required for thermonuclear fusion to take place?

6. Why do thermonuclear reactions occur only in the Sun’s core, not in its outer regions?

7. Describe how the net result of the reactions shown in the Cosmic Connections figure (Section 16-1) is the conversion of four protons into a single helium nucleus. What other particles are produced in this process? How many of each particle are produced?

8. Give an everyday example of hydrostatic equilibrium. Give an example of thermal equilibrium. Explain how these equilibrium conditions apply to each example.

9. If thermonuclear fusion in the Sun were suddenly to stop, what would eventually happen to the overall radius of the Sun? Justify your answer using the ideas of hydrostatic equilibrium and thermal equilibrium.

10. Give some everyday examples of conduction, convection, and radiative diffusion.

11. Describe the Sun’s interior. Include references to the main physical processes that occur at various depths within the Sun.

12. Suppose thermonuclear fusion in the Sun stopped abruptly. Would the intensity of sunlight decrease just as abruptly? Why or why not?

13. Explain how studying the oscillations of the Sun’s surface can give important, detailed information about physical conditions deep within the Sun.

14. What is a neutrino? Why is it useful to study neutrinos coming from the Sun? What do they tell us that cannot be learned from other avenues of research?

15. Unlike all other types of telescopes, neutrino detectors are placed deep underground. Why?

16. What was the solar neutrino problem? What solution to this problem was suggested by the results from the Sudbury Neutrino Observatory?

17. Describe the dangers in attempting to observe the Sun. How have astronomers learned to circumvent these observational problems?

18. Briefly describe the three layers that make up the Sun’s atmosphere. In what ways do they differ from one another?

19. What is solar granulation? Describe how convection gives rise to granules.

20. High-resolution spectroscopy of the photosphere reveals that absorption lines are blueshifted in the spectrum of the central, bright regions of granules but are redshifted in the spectrum of the dark boundaries between granules. Explain how these observations show that granulation is due to convection.

21. What is the difference between granules and supergranules?

22. What are spicules? Where are they found? How can you observe them? What causes them?

23. How do astronomers know that the temperature of the corona is so high?

24. How do astronomers know when the next sunspot maximum and minimum will occur?

25. Why do astronomers say that the solar cycle is really 22 years long, even though the number of sunspots varies over an 11-year period?

26. Explain how the magnetic-dynamo model accounts for the solar cycle.

27. Describe one explanation for why the corona has a higher temperature than the chromosphere.

28. Why should solar flares and coronal mass ejections be a concern for businesses that use telecommunication satellites?

Advanced Questions

Questions preceded by an asterisk (*) involve the topic discussed in Box 16-1.

29. Calculate how much energy would be released if each of the following masses were converted entirely into their equivalent energy: (a) a carbon atom with a mass of 2 × 10⁻²⁶ kg, (b) 1 kg, and (c) a planet as massive as Earth (6 × 10²⁴ kg).

30. Use the luminosity of the Sun (given in Table 16-1) and the answers to the previous question to calculate how long the Sun must shine in order to release an amount of energy equal to that produced by the complete mass-to-energy conversion of (a) a carbon atom, (b) 1 kg, and (c) Earth.

31. Assuming that the current rate of hydrogen fusion in the Sun remains constant, what fraction of the Sun’s mass will be converted into helium over the next 5 billion years? How will this affect the overall chemical composition of the Sun?

32. (a) Estimate how many kilograms of hydrogen the Sun has consumed over the past 4.56 billion years, and estimate the amount of mass that the Sun has lost as a result. Assume that the Sun’s luminosity has remained constant during that time. (b) In fact, the Sun’s luminosity when it first formed was only about 70% of its present value. With this in mind, explain whether your answers to part (a) are an overestimate or an underestimate.

33. *To convert 1 kg of hydrogen (¹H) into helium (⁴He) as described in Box 16-1, you must start with 1.5 kg of hydrogen. Explain why, and explain what happens to the other 0.5 kg. (Hint: How many ¹H nuclei are used to make the two ³He nuclei shown in the Cosmic Connections figure in Section 16-1? How many of these ¹H nuclei end up being incorporated into the ⁴He nucleus shown in the figure?)

34. *(a) A positron has the same mass as an electron (see Appendix 7). Calculate the amount of energy released by the annihilation of an electron and positron. (b) The products of this annihilation are two photons, each of equal energy. Calculate the wavelength of each photon, and confirm from Figure 5-7 that this wavelength is the gamma-ray range.

35. Sirius is the brightest star in the night sky. It has a luminosity of 23.5 L_⊙, that is, it is 23.5 times as luminous as the Sun and burns hydrogen at a rate 23.5 times greater than the Sun. How many kilograms of hydrogen does Sirius convert into helium each second?

36. (Refer to the preceding question.) Sirius has 2.3 times the mass of the Sun. Do you expect that the lifetime of Sirius will be longer, shorter, or the same length as that of the Sun? Explain your reasoning.

37. (a) If the Sun were not in a state of hydrostatic equilibrium, would its diameter remain the same? Explain your reasoning. (b) If the Sun were not in a state of thermal equilibrium, would its luminosity remain the same? What about its surface temperature? Explain your reasoning.

38. Using the mass and size of the Sun given in Table 16-1, verify that the average density of the Sun is 1410 kg/m³. Compare your answer with the average densities of the Jovian planets.

39. Use the data in Table 16-2 to calculate the average density of material within 0.1 R_⊙ of the center of the Sun. (You will need to use the mass and radius of the Sun as a whole, given in Table 16-1.) Explain why your answer is not the same as the density at 0.1 R_⊙ given in Table 16-2.

40. In a typical solar oscillation, the Sun’s surface moves up or down at a maximum speed of 0.1 m/s. An astronomer sets out to measure this speed by detecting the Doppler shift of an absorption line of iron with wavelength 557.6099 nm. What is the maximum wavelength shift that she will observe?

41. Explain why the results from the Sudbury Neutrino Observatory (SNO) only provide an answer to the solar neutrino problem for relatively high-energy neutrinos. (Hint: Can SNO detect solar neutrinos of all energies?)

42. The amount of energy required to dislodge the extra electron from a negative hydrogen ion is 1.2 × 10⁻¹⁹ J. (a) The extra electron can be dislodged if the ion absorbs a photon of sufficiently short wavelength. (Recall from Section 5-5 that the higher the energy of a photon, the shorter its wavelength.) Find the longest wavelength (in nm) that can accomplish this. (b) In what part of the electromagnetic spectrum does this wavelength lie? (c) Would a photon of visible light be able to dislodge the extra electron? Explain. (d) Explain why the photosphere, which contains negative hydrogen ions, is quite opaque to visible light but is less opaque to light with wavelengths longer than the value you calculated in (a).

43. Astronomers often use an H_α filter to view the chromosphere. Explain why this can also be accomplished with filters that are transparent only to the wavelengths of the H and K lines of ionized calcium. (Hint: The H and K lines are dark lines in the spectrum of the photosphere.)

44. Calculate the wavelengths at which the photosphere, chromosphere, and corona emit the most radiation. Explain how the results of your calculations suggest the best way to observe these regions of the solar atmosphere. (Hint: Treat each part of the atmosphere as a perfect blackbody. Assume average temperatures of 50,000 K and 1.5 × 10⁶ K for the chromosphere and corona, respectively.)

45. On November 15, 1999, the planet Mercury passed in front of the Sun as seen from Earth. The TRACE spacecraft made these time-lapse images of this event using ultraviolet light (top) and visible light (bottom). (Mercury moved from left to right in these images. The time between successive views of Mercury is 6 to 9 minutes.) Explain why the Sun appears somewhat larger in the ultraviolet image than in the visible-light image.

    

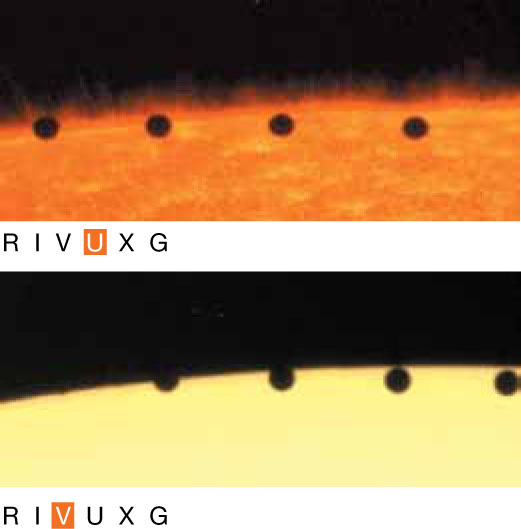    (K. Schrijver, Stanford-Lockheed Institute for Space Research, TRACE, and NASA)

46. The moving images on a television set that uses a tube (as opposed to a LCD or plasma flat-screen TV) are made by a fast-moving electron beam that sweeps over the back of the screen. Explain why placing a strong magnet next to the screen distorts the picture. (Caution: Do not try this with your television; it can cause permanent damage.)

47. Find the wavelength of maximum emission of the umbra of a sunspot and the wavelength of maximum emission of a sunspot’s penumbra. In what part of the electromagnetic spectrum do these wavelengths lie?

48. (a) Find the ratio of the energy flux from a patch of a sunspot’s penumbra to the energy flux from an equally large patch of undisturbed photosphere. Which patch is brighter? (b) Find the ratio of the energy flux from a patch of a sunspot’s penumbra to the energy flux from an equally large patch of umbra. Again, which patch is brighter?

49. Suppose that you want to determine the Sun’s rotation rate by observing its sunspots. Is it necessary to take Earth’s orbital motion into account? Why or why not?

50. (a) Using a ruler to make measurements of Figure 16-26, determine how far the arches in that figure extend above the Sun’s surface. The diameter of Earth is 12,756 km. (b) In Figure 16-26 (an ultraviolet image) the photosphere appears dark compared to the arches. Explain why.

51. The amount of visible light emitted by the Sun varies only a little over the 11-year sunspot cycle. But the number of X-rays emitted by the Sun can be 10 times greater at solar maximum than at solar minimum. Explain why these two types of radiation should be so different in their variability.

Discussion Questions

52. Discuss the extent to which cultures around the world have worshipped the Sun as a deity throughout history. Why do you suppose there has been such widespread veneration?

53. In the movie Star Trek IV: The Voyage Home, the starship Enterprise flies on a trajectory that passes close to the Sun’s surface. What features should a real spaceship have to survive such a flight? Why?

54. Discuss some of the difficulties in correlating solar activity with changes in Earth’s climate.

55. Describe some of the advantages and disadvantages of observing the Sun (a) from space and (b) from Earth’s south pole. What kinds of phenomena and issues might solar astronomers want to explore from these locations?

Web/eBook Questions

56. Search the World Wide Web for information about features in the solar atmosphere called sigmoids. What are they? What causes them? How might they provide a way to predict coronal mass ejections?

57. Determining the Lifetime of a Solar Granule. Accessand view the video “Granules on the Sun’s Surface” in Chapter 16 of the Universe Web site or eBook. Your task is to determine the approximate lifetime of a solar granule on the photosphere. Select an area, then slowly and rhythmically repeat “start, stop, start, stop” until you can consistently predict the appearance and disappearance of granules. While keeping your rhythm, move to a different area of the video and continue monitoring the appearance and disappearance of granules. When you are confident you have the timing right, move your eyes (or use a partner) to look at the clock shown in the video. Determine the length of time between the appearance and disappearance of the granules and record your answer.