11.2 Unit Tangent and Principal Unit Normal Vectors; Arc Length
767
OBJECTIVES
When you finish this section, you should be able to:
- Interpret the derivative of a vector function geometrically (p. 767)
- Find the unit tangent vector and the principal unit normal vector of a smooth curve (p. 768)
- Find the arc length of a curve traced out by a vector function (p. 770)
A vector function \(\mathbf{r}=\mathbf{r}(t)\) that is defined on a closed interval \(a\leq t\leq b\) traces out a curve as \(t\) varies over the interval. In this section, we analyze the curve geometrically by defining a tangent vector and a normal vector to the curve. We also express the arc length of a curve in terms of the unit tangent vector \(\mathbf{T}.\)
RECALL
The terms normal, perpendicular, and orthogonal all mean “meet at right angles.”
1 Interpret the Derivative of a Vector Function Geometrically
Suppose a vector function \(\mathbf{r}=\mathbf{r}(t)\) is defined on an interval \([ a,b]\) and is differentiable on \(( a,b).\) Then \(\mathbf{r}=\mathbf{r}( t)\) traces out a curve \(C\) as \(t\) varies over the interval. For a number \(t_{0}\), \(a<t_{0}<b,\) there is a point \(P_{0}\) on \(C\) given by the vector \(\mathbf{r}=\mathbf{r}(t_{0}).\) If \(h\neq 0\), there is a point \(Q\) on \(C\) different from \(P_{0}\) given by the vector \(\mathbf{r}(t_{0}+h).\) The vector \(\dfrac{\mathbf{r}(t_{0}+h)-\mathbf{r}(t_{0})}{h}\) can be thought of as a secant vector in the direction from \(P_{0}\) to \(Q\), as shown in Figure 8. Notice that whether \(h<0\) or \(h>0,\) the direction of the secant vectors follows the orientation of \(C.\)
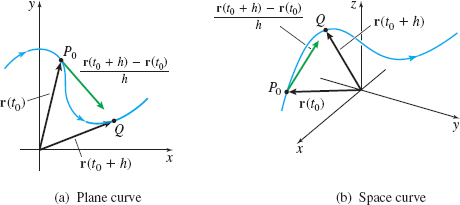
As \(h\rightarrow 0,\) the vector in the direction from \(P_{0}\) to \(Q\) moves along the curve \(C\) toward \(P_{0},\) getting closer and closer to the vector tangent to \(C\) at \(P_{0}\), as shown in Figure 9. The direction of the tangent vector follows the orientation of \(C.\) But as \(h\rightarrow 0,\) the vector \(\dfrac{\mathbf{r}( t_{0}+h) -\mathbf{r}( t_{0}) }{h}\) approaches the derivative \(\mathbf{r^{\prime} }( t_{0}) .\) This leads to the following definition.
Tangent vectors; \(\mathbf{r}^{\prime} (t_0)=\lim\limits_{h\rightarrow 0} \dfrac{\mathbf{r}(t_{0}+h)-\mathbf{r}(t_{0})}{h}\)768
NOTE
There is no tangent vector defined if \(\mathbf{r}^{\prime} (t_{0})=\mathbf{0}.\)
spanDEFINITIONspan Tangent Vector to a Curve \(C\)
Suppose \(\mathbf{r}=\mathbf{r}(t)\) is a vector function defined on the interval \([ a,b] \) and differentiable on the interval \(( a,b) .\) Let \(P_{0}\) be the point on the curve \(C\) traced out by \(\mathbf{r}=\mathbf{r}(t)\) corresponding to \(t=t_{0},\) \(a<t_{0}<b.\) If \(\mathbf{r}^{\prime} (t_{0})\neq \mathbf{0}\), then the vector \(\mathbf{r^{\prime} }( t_{0}) \) is a tangent vector to the curve at \(t_{0}.\) The line containing \(P_{0}\) in the direction of \(\mathbf{r}^{\prime} (t_{0})\) is the tangent line to the curve traced out by \(\mathbf{r}=\mathbf{r}(t)\) at \(t_{0}.\)
RECALL
The angle between two nonzero vectors \(\mathbf{v}\) and \(\mathbf{w}\) is determined by \(\cos \theta =\dfrac{\mathbf{v}\,{\cdot}\,\mathbf{w}} {\left\Vert \mathbf{v}\right\Vert \left\Vert \mathbf{w}\right\Vert }\), where \(0\leq \theta \leq \pi.\)
Finding the Angle Between a Tangent Vector to a Helix and the Direction \(\mathbf{k}\)
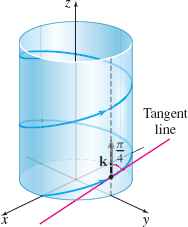
Show that the acute angle between the tangent vector to the helix \[ \mathbf{r}(t)=\cos t\mathbf{i}+\sin t\mathbf{j}+t\mathbf{k}\quad 0\,{\leq}\,t\,{\leq}\,2\pi \]
and the direction \(\mathbf{k}\) is \(\dfrac{\pi }{4}\) radian.
Solution A tangent vector at any point on the helix is given by \begin{equation*} \mathbf{r}^{\prime} (t)=-\sin t\mathbf{i}+\cos t\mathbf{j}+\mathbf{k} \end{equation*}
Then \(\left\Vert \mathbf{r}^{\prime} (t)\right\Vert\;= \sqrt{(-\sin t)^2 + \cos^2 t +1} = \sqrt{1+1} = \sqrt{2}.\)
The cosine of the acute angle \(\theta \) between \(\mathbf{r}^{\prime} (t)\) and \(\mathbf{k}\) is \begin{eqnarray*} &&\cos \theta =\frac{\mathbf{r}^{\prime} (t)\,{\cdot}\, \mathbf{k}}{\left\Vert \mathbf{r} ^{\prime} (t)\right\Vert \left\Vert \mathbf{k}\right\Vert }=\frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{2}\qquad \color{#0066A7}{\hbox{$\mathbf{r}^{\prime} (t)\,{\cdot}\, \mathbf{k} = 1$}}\\ \end{eqnarray*}
So, \(\theta =\dfrac{\pi }{4}\) radian. See Figure 10.
NOW WORK
Problems 9 and 15.
2 Find the Unit Tangent Vector and the Principal Unit Normal Vector of a Smooth Curve
We now state the definition of a smooth curve in terms of vector functions. You may wish to compare this definition with the one given in Section 9.2, p. 647.
spanDEFINITIONspan Smooth Curve
Let \(C\) denote a curve traced out by a vector function \(\mathbf{r}=\mathbf{r}(t)\) that is continuous for \(a\leq t\leq b.\) If the derivative \(\mathbf{r}^{\prime} (t)\) exists and is continuous on the interval \(( a,b) \) and if \(\mathbf{r}^{\prime} (t)\) is never \(\mathbf{0}\) on \(( a,b), \) then \(C\) is called a smooth curve.
Since \(\mathbf{r}^{\prime} ( t) \) is never \(\mathbf{0}\) for a smooth curve, such curves will have tangent vectors at every point.
The unit tangent vector and the unit normal vector are important for analyzing the geometry of a curve (Section 11.3) and for describing motion along a curve (Section 11.4).
For a smooth curve \(C\) traced out by the vector function \(\mathbf{r}=\mathbf{r}(t)\), \(a\leq t\leq b\), the unit tangent vector \(\mathbf{T}(t)\) to \(C\) at \(t\) is \begin{equation*} \bbox[5px, border:1px solid black, #F9F7ED] {\mathbf{T}(t)=\dfrac{\mathbf{r}^{\prime} (t)}{\left\Vert \mathbf{r}^{\prime} (t)\right\Vert}} \end{equation*}
769
Finding a Unit Tangent Vector to a Curve
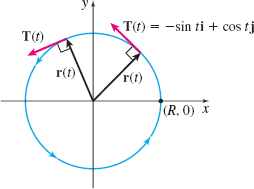
Show that the unit tangent vector \(\mathbf{T}(t)\) to the circle of radius \(R\) \begin{equation*} \mathbf{r}(t)=R\cos t\mathbf{i}+R\;\sin t\mathbf{j}\quad 0\leq t\leq 2\pi \end{equation*}
is everywhere orthogonal to \(\mathbf{r}(t).\) Graph \(\mathbf{r}=\mathbf{r}( t)\) and \(\mathbf{T}=\mathbf{T}( t).\)
Solution We begin by finding \(\mathbf{r}^{\prime} (t)\) and \(\left\Vert \mathbf{r}^{\prime} (t)\right\Vert\): \begin{eqnarray*} \mathbf{r}^{\prime} (t)& =&\dfrac{d}{dt}( R\cos t) \mathbf{i}+ \dfrac{d}{dt}( R\;\sin t) \mathbf{j}=-R\;\sin t\mathbf{i}+R\cos t\mathbf{j} \\[6pt] \left\Vert \mathbf{r}^{\prime} (t)\right\Vert & =&\sqrt{(-R\;\sin t)^{2}+(R\cos t)^{2}}=R \end{eqnarray*}
Then the unit tangent vector is \begin{equation*} \mathbf{T}(t)=\frac{\mathbf{r}^{\prime} (t)}{\left\Vert \mathbf{r}^{\prime} (t)\right\Vert }=\dfrac{-R\;\sin t\mathbf{i}+R\;\cos t\mathbf{j}}{R}=-\!\sin t\mathbf{i}+\cos t\mathbf{j} \end{equation*}
To determine whether \(\mathbf{r}( t)\) is orthogonal to \(\mathbf{T}( t), \) we find their dot product. \begin{equation*} \mathbf{T}(t)\,{\cdot}\, \mathbf{r}(t)=( -\!\sin t\mathbf{i}+\cos t\mathbf{j}) \,{\cdot}\, ( R\;\cos t\mathbf{i}+R\;\sin t\mathbf{j}) =-R\;\sin t\cos t+R\;\sin t\cos t=0 \end{equation*}
for all \(t.\) That is, \(\mathbf{T}(t)\) is everywhere orthogonal to \(\mathbf{r}(t)\), as shown in Figure 11.
The following discussion leads to the definition of the principal unit normal vector.
Suppose a smooth curve \(C\) is traced out by a twice differentiable vector function \(\mathbf{r}=\mathbf{r}(t).\) Then the unit tangent vector \(\mathbf{T}(t)\) is differentiable. Also, since \(\mathbf{T}(t)\) is a unit vector, \[ \mathbf{T}(t)\,{\cdot}\, \mathbf{T}(t)=1\quad \hbox{for all}\,t \]
If we differentiate this expression, we find \[ \begin{array}{rcl@{\qquad}l} \dfrac{d}{dt}[\mathbf{T}(t)\,{\cdot}\, \mathbf{T}(t)]& =&\dfrac{d}{dt}( 1) & \color{#0066A7}{\hbox{Differentiate both sides.}} \\[12pt] \mathbf{T}^{\prime} (t)\,{\cdot}\, \mathbf{T}(t)+\mathbf{T}(t)\,{\cdot}\, \mathbf{T}^{\prime} (t) &=& 0 & \color{#0066A7}{\hbox{Use the dot product rule.}} \\[6pt] \mathbf{T}(t)\,{\cdot}\, \mathbf{T}^{\prime} (t)& =&0 & \color{#0066A7}{\hbox{Simplify.}} \end{array} \]
We conclude that \(\mathbf{T}^{\prime} (t)\) is a vector that is orthogonal to \(\mathbf{T}(t)\) at every point on the \(C\). In particular, the vector \(\dfrac{\mathbf{T}^{\prime} (t)}{\left\Vert \mathbf{T}^{\prime} (t)\right\Vert }\) is a unit vector that is orthogonal to \(\mathbf{T}(t)\) at every point on the curve \(C.\)
spanDEFINITIONspan Principal Unit Normal Vector
For a smooth curve \(C\) traced out by a vector function \(\mathbf{r}=\mathbf{r}(t),\) \(a\leq t\leq b,\) that is twice differentiable for \(a<t<b,\) the principal unit normal vector \(\mathbf{N}(t)\) to \(C\) at \(t\) is \begin{equation*} \bbox[5px, border:1px solid black, #F9F7ED] {\mathbf{N}(t)=\dfrac{\mathbf{T}^{\prime} (t)}{\left\Vert \mathbf{T}^{\prime} (t)\right\Vert }} \end{equation*}
Notice that the unit normal vector \(\mathbf{N}\) is not defined if \(\mathbf{T^{\prime} =0.}\) So, for example, lines do not have well-defined unit normals.
If \(C\) is a plane curve, there are two unit vectors that are orthogonal to the unit tangent vector \(\mathbf{T}\), as shown in Figure 12(a). If \(C\) is a curve in space, there are infinitely many unit vectors that are orthogonal to the unit tangent vector \(\mathbf{T}\), as shown in Figure 12(b). The definition of the principal unit normal vector identifies exactly one of the orthogonal vectors and gives it a name.
770
Finding the Principal Unit Normal Vector
Find the principal unit normal vector \(\mathbf{N}(t)\) to the circle \(\mathbf{r}( t) =R\;\cos t\mathbf{i}+R\;\sin t\mathbf{j}\), \(0\leq t\leq 2\pi .\) (Refer to Example 2.) Graph \(\mathbf{r}=\mathbf{r}( t), \) and show a unit tangent vector and a unit normal vector.
Solution From Example 2, the unit tangent vector \(\mathbf{T}(t)\) is \begin{equation*} \mathbf{T}(t)=-\!\sin t\mathbf{i}+\cos t\mathbf{j} \end{equation*}
\(\mathbf{r}( t) =R\;\cos t\mathbf{i}+R\;\sin t\mathbf{j,} \\ 0\leq t\leq 2\pi \)Since \(\mathbf{T}^{\prime} ( t) =-\cos t\mathbf{i}-\sin t\mathbf{j},\) the principal unit normal vector \(\mathbf{N}(t)\) is \begin{equation*} \mathbf{N}(t)=\frac{\mathbf{T}^{\prime} (t)}{\left\Vert \mathbf{T}^{\prime} (t)\right\Vert }=\frac{-\!\cos t\mathbf{i}-\sin t\mathbf{j}}{\sqrt{(-\!\cos t)^{2}+(-\!\sin t)^{2}}}=-\cos t\mathbf{i}-\sin t\mathbf{j} \end{equation*}
Since \(\mathbf{r}( t) = R ( \cos t\mathbf{i}+\sin t\mathbf{j}), \) the vector \(\mathbf{N}( t)\) is parallel to \(-\mathbf{r}(t)\). That is, \(\mathbf{N}(t)\) is a unit vector opposite in direction to the vector \(\mathbf{r}(t)\), so \(\mathbf{N}\) is directed toward the center of the circle, as shown in Figure 13.
NOW WORK
Problem 29.
Finding the Principal Unit Normal Vector of a Helix
Show that the principal unit normal vector \(\mathbf{N}(t)\) of the helix \begin{equation*} \mathbf{r}(t)=\cos t\mathbf{i}+\sin t\mathbf{j}+t\mathbf{k} \end{equation*}
is orthogonal to the \(z\)-axis.
Solution We begin by finding \(\mathbf{r^{\prime} }( t) \) and \(\left\Vert \mathbf{r}^{\prime} ( t)\right \Vert.\) \[ \begin{equation*} \mathbf{r}^{\prime} (t)=-\!\sin t\mathbf{i}+\cos t\mathbf{j}+\mathbf{k}\qquad \left\Vert \mathbf{r}^{\prime }(t)\right\Vert =\sqrt{ (-\!\sin t)^{2}+(\cos t)^{2}+1}=\sqrt{2} \end{equation*} \]
Then the unit tangent vector is \(\mathbf{T}(t)=\dfrac{\mathbf{r}^{\prime }(t)}{||\mathbf{r}^{\prime }(t)||}=\dfrac{-\!\sin t\mathbf{i}+\cos t\mathbf{j}+\mathbf{k}}{\sqrt{2}}.\)
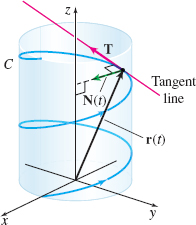
Since \[ \begin{equation*} \mathbf{T}^{\prime} (t)=\dfrac{-\!\cos t\mathbf{i}-\sin t\mathbf{j}}{\sqrt{2} }\qquad \hbox{and}\qquad \left\Vert \mathbf{T}^{\prime }(t)\right\Vert =\sqrt{ \left( -\dfrac{\cos t}{\sqrt{2}}\right) ^{2}+\left( -\dfrac{\sin t}{\sqrt{2}} \right) ^{2}}=\dfrac{1}{\sqrt{2}} \end{equation*} \]
we have \begin{equation*} \mathbf{N}(t)=\dfrac{\mathbf{T}^{\prime} (t)}{\left\Vert \mathbf{T}^{\prime} (t)\right\Vert }=-\!\cos t\mathbf{i}-\sin t\mathbf{j} \end{equation*}
Since the direction of the \(z\)-axis is \(\mathbf{k}\), it follows that \(\mathbf{N}(t)\,{\cdot}\, \mathbf{k}=0\) for all \(t.\) So, \(\mathbf{N}(t)\) is always orthogonal to the \(z\)-axis, as shown in Figure 14.
NOW WORK
Problem 37.
3 Find the Arc Length of a Curve Traced Out by a Vector Function
A formula for the arc length of a smooth plane curve was derived in Chapter 9. The formula for the arc length of a smooth curve traced out by a vector function is given next.
THEOREM Arc Length of a Vector Function
If a smooth curve \(C\) is traced out by the vector function \(\mathbf{r}=\mathbf{r}(t),\) \(a\leq t\leq b\), the arc length \(s\) along \(C\) from \(t=a\) to \(t=b\) is \begin{equation*} \bbox[5px, border:1px solid black, #F9F7ED] {s=\int_{a}^{b}\left\Vert \mathbf{r}^{\prime} (t)\right\Vert dt} \end{equation*}
771
For a smooth plane curve \(C\), traced out by \[ \mathbf{r}(t)=x(t)\mathbf{i}+y(t)\mathbf{j}\qquad a\leq t\leq b \]
we have \[ \mathbf{r}^{\prime} (t)=\dfrac{dx}{dt}\mathbf{i}\,{+}\,\dfrac{dy}{dt}\mathbf{j}\qquad \hbox{and}\qquad \left\Vert \mathbf{r^{\prime} }( t)\right\Vert =\;\sqrt{ \left( \dfrac{dx}{dt}\right) ^{2}+\left( \dfrac{dy}{dt}\right) ^{2}} \]
NEED TO REVIEW?
The arc length of a smooth curve is discussed in Section 9.2, pp. 651-653.
The arc length of \(C\) from \(a\) to \(b\) is given by \begin{equation*} s=\int_{a}^{b}\sqrt{\left( \dfrac{dx}{dt}\right) ^{2}+\left( \dfrac{dy}{dt} \right) ^{2}}\,\,dt=\int_{a}^{b}\Vert \mathbf{r}^{\prime} ( t) \Vert dt \end{equation*}
For a smooth space curve \(C\), traced out by \[ \mathbf{r}(t)=x(t)\mathbf{i}+y(t)\mathbf{j}+z(t)\mathbf{k}\qquad a\leq t\leq b \]
we have \[ \mathbf{r^{\prime} }(t)=\dfrac{dx}{dt}\mathbf{i}+\dfrac{dy}{dt}\mathbf{j}+ \dfrac{dz}{dt}\mathbf{k}\qquad \hbox{and}\qquad \left\Vert \mathbf{r^{\prime} }( t) \right\Vert =\sqrt{\left( \dfrac{dx}{dt}\right) ^{2}+\left( \dfrac{ dy}{dt}\right) ^{2}+\left( \dfrac{dz}{dt}\right) ^{2}} \]
The arc length of \(C\) from \(a\) to \(b\) is given by \begin{equation*} s=\int_{a}^{b}\sqrt{\left( \dfrac{dx}{dt}\right) ^{2}+\left( \dfrac{dy}{dt} \right) ^{2}+\left( \dfrac{dz}{dt}\right) ^{2}}\,\,dt=\int_{a}^{b}\left\Vert \mathbf{r}^{\prime} ( t) \right\Vert dt \end{equation*}
Finding the Arc Length of a Circle and a Helix
Find the arc length of:
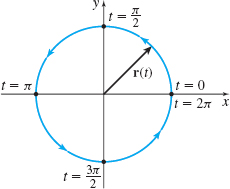
(a) The circle \(\mathbf{r}(t)=R\;\cos t\mathbf{i}+R\;\sin t\mathbf{j}\) from \(t=0\) to \(t=2\pi \)
(b) The circular helix \(\mathbf{r}(t)=R\;\cos t\mathbf{i}+R\;\sin t\mathbf{j}+t\mathbf{k}\) from \(t=0\) to \(t=2\pi \)
Solution (a) We begin by finding \(\mathbf{r^{\prime} }( t)\) and \(\left\Vert \mathbf{r^{\prime} }( t) \right\Vert \): \[ \mathbf{r}^{\prime} (t)=-R\;\sin t\mathbf{i}+R\;\cos t\mathbf{j}\qquad \left\Vert \mathbf{r}^{\prime} (t)\right\Vert =\sqrt{(-R\;\sin t)^{2}+(R\;\cos t)^{2}}=R \]
Now we use the formula for arc length. \begin{equation*} s=\int_{a}^{b}\left\Vert \mathbf{r}^{\prime} (t)\right\Vert dt=\int_{0}^{2\pi }Rdt=\big[ R\hbox{ }t\big] _{0}^{2\pi }=2\pi R \end{equation*}
which is the familiar formula for the circumference of a circle. See Figure 15.
(b) We begin by finding \(\mathbf{r^{\prime} }( t)\) and \(\left\Vert \mathbf{r^{\prime} }( t) \right\Vert.\) \begin{eqnarray*} \mathbf{r}^{\prime} (t) &=&-R\;\sin t\mathbf{i}\,{+}\,R\;\cos t\mathbf{j}+\mathbf{k},\\[6pt] \left\Vert \mathbf{r}^{\prime} (t)\right\Vert &=& \sqrt{\!(-R\;\sin t)^{2}\,{+}\,(R\;\cos t)^{2}\,{+}\,1^{2}}\,{=}\,\sqrt{R^{2}\,{+}\,1} \end{eqnarray*}
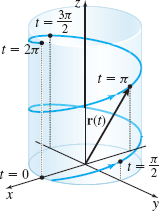
Then \begin{equation*} ~s=\int_{a}^{b}\left\Vert \mathbf{r}^{\prime} ( t) \right\Vert dt=\int_{0}^{2\pi }\sqrt{R^{2}+1}~dt=\left[ \sqrt{R^{2}+1}\,t\right] _{0}^{2\pi }=2\pi \sqrt{R^{2}+1} \end{equation*}
See Figure 16.
NOW WORK
Problem 51.
For most vector functions, finding arc length requires technology.
772
Using Technology to Find the Arc Length of an Ellipse
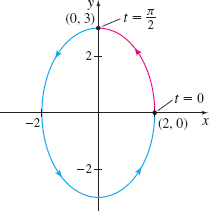
Use technology to find the arc length \(s\) of the ellipse shown in Figure 17 traced out by the vector function \(\mathbf{r}( t) =2\cos t\mathbf{i}+3\sin t\mathbf{j}\) from \(t=0\) to \(t=\dfrac{\pi }{2}.\)
Solution We begin by finding \(\mathbf{r^{\prime} }( t) \) and \(\left\Vert \mathbf{r^{\prime} }( t) \right\Vert .\) \[ \mathbf{r}^{\prime} (t)=-2\sin t\mathbf{i}+3\cos t\mathbf{j}\qquad \left\Vert \mathbf{r}^{\prime} (t)\right\Vert =\sqrt{4\sin ^{2}t+9\cos ^{2}t} \]
Now we use the formula for arc length. \begin{equation*} s=\int_{a}^{b}\left\Vert \mathbf{r}^{\prime} (t)\right\Vert dt=\int_{0}^{\pi /2}\sqrt{4\sin ^{2}t+9\cos ^{2}t}\,dt \end{equation*}
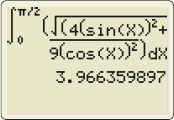
This is an integral that has no antiderivative in terms of elementary functions. To obtain a numerical approximation to the arc length, we use a CAS or a graphing utility.
When entering the integral in WolframAlpha, we find \begin{equation*} \int_{0}^{\pi /2}\sqrt{4\sin ^{2}t+9\cos ^{2}t}\,dt\approx 3.96636 \end{equation*}
If we use a TI-84 to find the value of this integral, we obtain the same result. The screen shot is given in Figure 18.
NOW WORK
Problem 55.