14.3 Double Integrals Using Polar CoordinatesPrinted Page 923
OBJECTIVES
When you finish this section, you should be able to:
Suppose the function \(z=f(x,y)\) is continuous on a closed, bounded region \(R.\) Then the double integral, \(\iint\limits_{\kern-3ptR}f(x,y)\, {\it dA}\) exists, and \({\it dA}={\it dx}\, {\it dy}={\it dy}\,{\it dx}\) is the differential of the area \(A\) of \(R.\) If the region \(R\) is enclosed by rays (lines through the origin) and parts of circles, it is often easier to find \(\iint\limits_{\kern-3ptR}f(x,y) \, {\it dA}\) by converting to polar coordinates. We convert a function \( z=f(x,y)\) to polar coordinates \((r,\theta)\) by using the equations \(x=r\cos \theta\), \(y=r\sin \theta\). It remains to find the differential \({\it dA}\) of area \(A\) in polar coordinates.
NEED TO REVIEW?
Polar coordinates are discussed in Section 9.4, pp. 661-668.
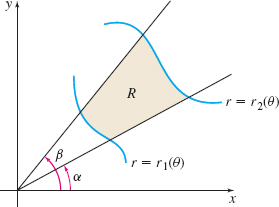
Suppose the closed, bounded region \(R\) is enclosed by the rays \(\theta =\alpha\) and \(\theta =\beta\), where \(0\leq \alpha \lt \beta \lt 2\pi\), and the smooth curves \(r=r_{1}(\theta)\) and \(r=r_{2}(\theta),\) where \(0\leq r_{1}\leq r_{2}\). See Figure 23.
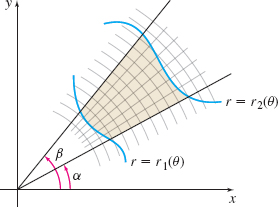
We partition \(R\) using rays from \(\theta =\alpha\) to \(\theta =\beta\) and using concentric circles centered at the origin, as shown in Figure 24. The result is a collection of polar subregions. Let \(n\) denote the number of these polar subregions that lie entirely in \(R\). They form a partition \(P\) of \(R.\)
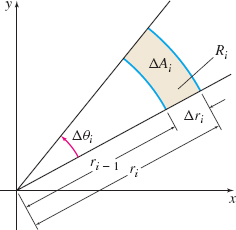
Consider a typical polar subregion \(R_{i}\) as shown in Figure 25. The area \(\Delta A_{i}\) of this subregion is the difference of the areas of two circular sectors. \[ \begin{eqnarray*} \Delta A_{i}&=&\dfrac{1}{2} r_{i}^{2}\Delta \theta _{i}-\dfrac{1}{2}r_{i-1}^{2}\Delta \theta _{i} = \dfrac{1}{2}\big(r_{i}^{2}-r_{i-1}^{2}\big)\Delta \theta _{i}=\dfrac{1}{2} (r_{i}+r_{i-1})(r_{i}-r_{i-1})\Delta \theta _{i} \\[-6pt] & \underset{{\color{#0066A7}{\hbox{Area \(A\) of a sector \(=\dfrac{1}{2}{r}^{2}{\theta}\)}}}}{\color{#0066A7}{\uparrow}}\\ &=&\dfrac{1}{2}(r_{i}+r_{i-1})\Delta r_{i}\Delta \theta _{i} \qquad {\color{#0066A7}{\hbox{\(\Delta r_i=r_{i}-r_{i-1}\)}}} \end{eqnarray*} \]
924
Next we choose a point \((\bar{r}_{i},\bar{\theta}_{i})\) in the polar subregion \(R_{i}\) so that \(\bar{r}_{i}=\dfrac{1}{2}( r_{i}+r_{i-1}) \). Then the area \(\Delta A_{i}\) of \(R_{i}\) is \[\bbox[5px, border:1px solid black, #F9F7ED]{ \Delta A_{i}=\bar{r}_{i}\Delta r_{i}\Delta \theta _{i} } \]
and the differential \({\it dA}\) is \[\bbox[5px, border:1px solid black, #F9F7ED]{ {\it dA}=r\,{\it dr}\,d\theta } \]
It can be shown that if \(f\) is continuous on the region \(R\), then \[ \iint\limits_{\kern-3ptR}f(x,y)\,{\it dA}=\displaystyle\iint\limits_{\kern-3ptR}f(r\cos \theta ,r\sin \theta )~r\,{\it dr}\,d\theta \]
1 Find a Double Integral Using Polar CoordinatesPrinted Page 924
As with double integrals in rectangular coordinates, certain regions in polar coordinates will lead to iterated integrals.
THEOREM Iterated Double Integral in Polar Coordinates
Let the function \(z=f(x,y)\) be continuous over a closed, bounded region \(R\). Suppose \(R\) is enclosed by the rays \(\theta =\alpha\) and \(\theta =\beta\) and the curves \(r=r_{1}(\theta)\) and \( r=r_{2}(\theta)\), where \(0\leq r_{1}\leq r_{2}.\) If \(r=\) \(r_{1}(\theta)\) and \(r=r_{2}(\theta)\) are continuous for \(\alpha \leq \theta \leq \beta\), then \[\bbox[5px, border:1px solid black, #F9F7ED]{ \displaystyle\iint\limits_{\kern-3ptR}f(x,y) \,{\it dA}=\displaystyle\iint\limits_{\kern-3ptR}f(r\cos\theta,r\sin\theta)\, {\it dA} =\int_{\alpha }^{\beta }\int_{r_{1}(\theta) }^{r_{2}(\theta) }f(r\cos\theta,r\sin\theta)\, r\,dr\,d\theta } \]
Notice that we wrote the iterated double integral without using brackets to indicate the order of integration. In the iterated integral, \(dr\) appears before \(d\theta;\) this indicates that we integrate with respect to \( r\) before we integrate with respect to \(\theta\). In finding the inside integral \(\int_{r_{1}(\theta )}^{r_{2}(\theta )}f(r \cos \theta, r \sin \theta )\, r\,dr\), we treat \(\theta\) as a constant and integrate partially with respect to \(r\).
EXAMPLE 1Finding a Double Integral Using Polar Coordinates
Find \(\displaystyle\iint\limits_{\kern-3ptR}\cos \theta \,{\it dA}\), where \(R\) is the region enclosed by the rays \(\theta =0\) and \(\theta =\dfrac{\pi }{4}\) and the circle \(r=4\cos \theta\).
Solution We begin with a graph of the region \(R\). See Figure 26. Notice that \(\theta\) varies from \(0\) to \(\dfrac{\pi }{4}\) and \(r\) varies from \(r_{1}=0\) to the circle \(r_{2}=4\cos \theta\). Then \[ \begin{array} \displaystyle\iint\limits_{\kern-3ptR}\cos \theta \,{\it dA} &=&\int_{0}^{\pi /4}\int_{0}^{4\cos \theta }r\cos \theta \,dr\,d\theta =\int_{0}^{\pi /4}\left[ \dfrac{r^{2}}{2}\cos \theta \right] _{0}^{4\cos \theta }d\theta =\int_{0}^{\pi /4}8\cos ^{3}\theta \,d\theta \notag \\[4pt] &=&8\int_{0}^{\pi /4}(1-\sin ^{2}\theta )\cos \theta \,d\theta = 8\int_{0}^{\sqrt{2}/2}(1-u^{2})\, du\\[-8pt] && \qquad \qquad \qquad \quad \underset{\color{#0066A7}{\hbox{\(u=\sin \theta ;\, {du}=\cos \theta\, d\theta\)}}}{\color{#0066A7}{\uparrow }}\\[8pt] &=&8\left[ u-\dfrac{u^{3}}{3}\right] _{0}^{\sqrt{2}/2}=8\left[ \dfrac{\sqrt{2} }{2}-\dfrac{\sqrt{2}}{12}\right] =\dfrac{10\sqrt{2}}{3} \end{array} \]
NEED TO REVIEW?
Integrals containing trigonometric functions are discussed in Section 7.2, pp. 480-486.
NOW WORK
925
When the integrand of a double integral \(\iint\limits_{\kern-3ptR}f(x,y)\,{\it dA}\) is a function of \(x^{2}+y^{2}\), it is sometimes easier to integrate using polar coordinates than using rectangular coordinates.
NOTE
The order \({\it dy}\,{\it dx}\) indicates the integration is done with respect to \(y\) first, then with respect to \(x\).
EXAMPLE 2Finding an Iterated Integral Using Polar Coordinates
Find the iterated integral \(\int_{0}^{2}\int_{0}^{\sqrt{4-x^{2}} }(x^{2}+y^{2})\,{\it dy}\,{\it dx}\).
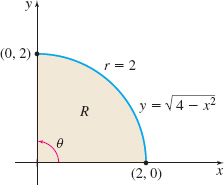
\(0\leq x\leq 2\) \(0\leq r\leq 2\),
\(0\leq \theta \leq \dfrac{\pi}{2}\)
Solution The region \(R\) is enclosed by the graph of \(y=\sqrt{ 4-x^{2}}\), (a portion of a circle of radius 2), \(0\leq x\leq 2\), and the positive \(x\)- and \(y\)-axes. See Figure 27. In polar coordinates, this region \(R\) is given by \(0\leq r\leq 2\) and \(0\leq \theta \leq \dfrac{\pi }{2} \). Then \[ \begin{eqnarray*} \int_{0}^{2}\int_{0}^{\sqrt{4-x^{2}}}(x^{2}+y^{2})\,{\it dy}\,{\it dx}&=&\displaystyle\iint\limits_{\kern-3ptR}(x^{2}+y^{2}) \, {\it dA}\\[4pt] &=&\displaystyle\iint\limits_{\kern-3ptR}r^{2}r\,{\it dr}\,d\theta\qquad{\color{#0066A7}{\hbox{$x^2 + y^2=r^2;\quad {dA}=r\,{dr}\,d\theta$}}}\\[4pt] &=&\int_{0}^{\pi /2}\int_{0}^{2}r^{3}\,dr\,d\theta =\int_{0}^{\pi /2}\left[\dfrac{r^{4}}{4}\right] _{0}^{2}\,d\theta\\[4pt] &=&\int_{0}^{\pi /2}4\,d\theta = \big[ 4\theta \big] _{0}^{\pi /2}=2\pi \end{eqnarray*} \]
NOW WORK
There are occasions when using polar coordinates converts an integral that is not expressible in terms of elementary functions to an integral that can be written in terms of elementary functions.
NEED TO REVIEW?
Elementary functions are discussed in Section 7.6, p. 508.
EXAMPLE 3Finding a Double Integral Using Polar Coordinates
Find \(\displaystyle\iint\limits_{\kern-3ptR}e^{x^{2}+y^{2}}\,d\!A\), where \(R\) is the region in the first quadrant inside the circle \(x^{2}+y^{2}=a^{2}\).
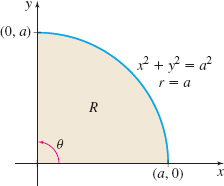
Solution In rectangular coordinates, \(\iint \limits_{\kern-3ptR}e^{x^{2}+y^{2}}\,d\!A\) only can be approximated using numerical techniques. But the presence of \(x^{2}+y^{2}\) in the integrand and the fact that the region \(R\) has part of a circle as its boundary suggest using polar coordinates. Figure 28 shows the region \(R.\) We use polar coordinates to obtain 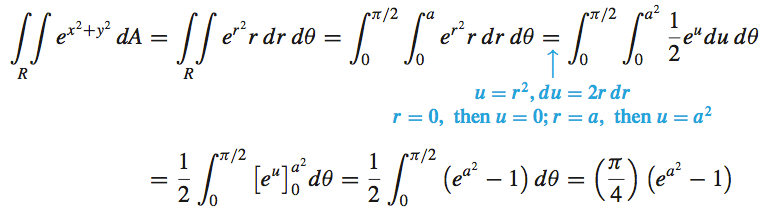
NOW WORK
2 Find Area and Volume Using Polar CoordinatesPrinted Page 925
Suppose \(z=f(x,y)\geq 0\), where \(f\) is continuous over a closed, bounded region \(R\). Then the double integral \(\iint\limits_{\kern-3ptR}f(x,y)\,{\it dA}=\iint\limits_{\kern-3ptR} f(r\cos\theta,r\sin\theta)\,r\,dr\,d\theta\) represents the volume \(V\) of the solid under the surface \(z=f(x,y)\) and above the region \(R\).
926
EXAMPLE 4Finding the Volume of a Solid
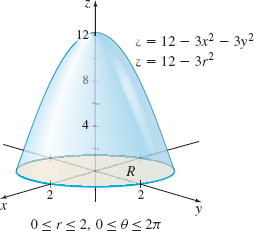
Find the volume \(V\) of the solid under the circular paraboloid \( z=12-3x^{2}-3y^{2}\) and above the \(xy\)-plane.
Solution We begin by graphing the paraboloid for \(z\geq 0,\) as shown in Figure 29.
The region \(R\) is determined by the intersection of the surface \(z\) and the \( xy\)-plane. So, we let \(z=0\) and simplify the equation. \begin{eqnarray*} 12-3x^{2}-3y^{2} &=&0 \\[3pt] 3x^{2}+3y^{2} &=&12 \\[3pt] x^{2}+y^{2} &=&4 \end{eqnarray*}
So \(R\) is the region enclosed by the circle \(x^{2}+y^{2}=4\).
To convert the problem to polar coordinates, we let \(x=r\cos \theta\) and \( y=r\sin \theta.\) Then the paraboloid is \(z=12-3x^{2}-3y^{2}=12-3(x^{2}+y^{2}) =12-3r^{2},\) and the region \(R\) is enclosed by the circle \(r^{2}=4.\) So, \(R\) is given by \(0\leq r\leq 2\) and \(0\leq \theta \leq 2\pi.\)
Then \[ \begin{eqnarray*} V &=&\displaystyle\iint\limits_{\kern-3ptR}( 12-3x^{2}-3y^{2})\, {\it dA}\underset{\underset{\color{#0066A7}{\hbox{$\begin{array}{c}3x^{2}+3y^{2}=3r^{2}\\ {dA}=r\,{dr}\,d\theta\end{array}$}}} {\color{#0066A7}{\uparrow}}}{=} \int\nolimits_{0}^{2\pi }\!\!\!\int_{0}^{2}( 12-3r^{2})\, r\,{\it dr}\,d\theta = \int_{0}^{2\pi }\!\!\!\int_{0}^{2}( 12r-3r^{3})\, dr\, d\theta \\[-15.5pt] &=&\int_{0}^{2\pi }\left[ 6r^{2}-3\dfrac{r^{4}}{4}\right] _{0}^{2}~d\theta = \int_{0}^{2\pi }12~d\theta =\big[ 12\theta \big] _{0}^{2\pi }=24\pi \hbox{ cubic units} \end{eqnarray*} \]
NOW WORK
EXAMPLE 5Finding the Volume of a Solid
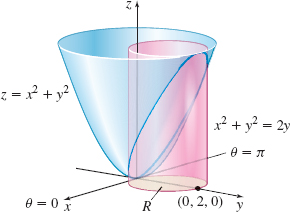
Find the volume \(V\) of the solid under the surface \(z=x^{2}+y^{2}\), above the \(xy\)-plane, and inside the cylinder \(x^{2}+y^{2}=2y\).
Solution See Figure 30. The volume we seek lies above the region \(R\) in the \(xy\)-plane enclosed by the circle \(x^{2}+y^{2}=2y\), whose center is at \((0,1,0)\) and whose radius is 1. To convert to polar coordinates, we let \(x=r\cos \theta\) and \(y=r\sin \theta\). Then the region \(R\) is enclosed by \[ \begin{eqnarray*} x^{2}+y^{2} &=&2y \\[3pt] r^{2}\cos ^{2}\theta +r^{2}\sin ^{2}\theta &=&2r\sin \theta \\[3pt] r^{2} &=&2r\sin \theta \\[3pt] r &=&2\sin \theta \end{eqnarray*} \]
The region \(R\) is bounded by \(0\leq r\leq 2\sin \theta\) and \(0\leq \theta \leq \pi .\)
The volume \(V\) under \(z=x^{2}+y^{2}=r^{2}\), above the \(xy\)-plane, and over \(R\) is \[ \begin{eqnarray*} V &=&\displaystyle\iint\limits_{\kern-3ptR} (x^2+y^2)\,dA =\displaystyle\iint\limits_{\kern-3ptR}r^{2}r\,{\it dr}\,d\theta =\int_{0}^{\pi }\int_{0}^{2\sin \theta }r^{3}\,dr\,d\theta =\int_{0}^{\pi }\left[ \dfrac{r^{4}}{4}\right] _{0}^{2\sin \theta }d\theta \\[4pt] &=&4\int_{0}^{\pi }\sin ^{4}\theta \,d\theta =4\int_{0}^{\pi }\left( \dfrac{ 1-\cos (2\theta) }{2}\right) ^{2} d\theta \\[4pt] &=&\int_{0}^{\pi }[ 1-2\cos (2\theta) +\cos ^{2}(2\theta) ] \,d\theta =\int_{0}^{\pi }\left[ 1-2\cos (2\theta) +\dfrac{1+\cos ( 4\theta ) }{2}\right]\! d\theta \\[4pt] &=&\left[ \theta -\sin (2\theta) +\dfrac{1}{2}\theta +\dfrac{1}{ 2}\cdot \dfrac{\sin ( 4\theta )}{4} \right] _{0}^{\pi }=\dfrac{3\pi }{2} \hbox{ cubic units} \end{eqnarray*} \]
NEED TO REVIEW?
Integrals containing trigonometric functions are discussed in Section 7.2, pp. 480-486.
NOW WORK
927
The double integral \(\iint\limits_{\kern-3ptR}\, {\it dA} =\iint\limits_{\kern-3ptR}r\,dr\,d\theta\) represents the volume of a solid whose height is \(1\). As a result, the area \(A\) of the region \(R\) is numerically equal to \[\bbox[5px, border:1px solid black, #F9F7ED]{ A=\displaystyle\iint\limits_{\kern-3ptR}r\,dr\,d\theta } \]
EXAMPLE 6Finding the Area Enclosed by a Cardioid
Use double integration to find the area enclosed by the cardioid \(r=a(1-\cos \theta)\).
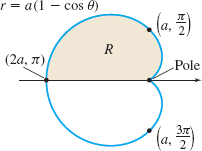
Solution The cardioid \(r=a(1-\cos \theta)\) is shown in Figure 31. Using symmetry, the area enclosed by the cardioid is twice the area of the shaded region \(R\) in Figure 31. So, \[ \begin{equation*} A=2\displaystyle\iint\limits_{\kern-3ptR}r\,dr\,d\theta \end{equation*} \]
where the region \(R\) is given by \(0\leq r\leq a( 1-\cos \theta )\) and \(0\leq \theta \leq \pi.\) Then \begin{eqnarray*} A &=&2\int_{0}^{\pi }\int_{0}^{a(1-\cos \theta )}r\,dr\,d\theta =2\int_{0}^{\pi }\left[ \dfrac{r^{2}}{2}\right] _{0}^{a( 1-\cos \theta ) }d\theta\\[4pt] &=&\int_{0}^{\pi }a^{2}( 1-\cos \theta ) ^{2}\,d\theta =a^{2}\int_{0}^{\pi }( 1-2\cos \theta +\cos ^{2}\theta )\, d\theta\\[4pt] &=&a^{2}\!\left[ \theta -2\sin \theta +\left( \dfrac{\theta }{2}+\dfrac{\sin (2\theta) }{4}\right) \right] _{0}^{\pi }=\dfrac{3}{2}\pi a^{2} \hbox{ square units} \end{eqnarray*}