OBJECTIVES

When you finish this section, you should be able to:

1. Find integrals of the form \(\int \hbox{sin}^{n}x {dx}\) or \(\int \hbox{cos} ^{ n} x\,{dx}\), \(n \ge\) 2 an integer (p. 480)
2. Find integrals of the form \(\int \hbox{sin}^{m} x \hbox{cos}^{n} x {dx}\) (p. 483)
3. Find integrals of the form \(\int {tan}^{m}x {sec}^{n}x {dx}\) or \(\int {cot}^{m} x {csc}^{n}x {dx}\) (p. 483)
4. Find integrals of the form \(\int \hbox{sin}{(ax)} \hbox{sin}{(bx)}{dx}\), \(\int \hbox{sin}{(ax)} \hbox{cos}{(bx)}{dx}\), or \(\int \hbox{cos}{(ax)} \hbox{cos}{(bx)} {dx}\) (p. 485)

Finding the Integral \(\int \sin^{5}x\,dx\)

Find \(\int \sin ^{5}x\,dx\).

Solution Since the exponent 5 is odd, we write \(\int \sin ^{5}x\,dx=\int \sin ^{4}x \sin x\,dx\), and use the identity \(\sin ^{2}x=1-\cos ^{2}x\). \[ \begin{eqnarray*} \int \sin ^{5}x\,dx&=&\int \sin ^{4}x\sin x\,dx=\int (\sin ^{2}x) ^{2}\sin x\,dx=\int (1-\cos ^{2}x)^{2}\sin x\,dx\\[4pt] &=&\int (1-2\cos ^{2}x+\cos ^{4}x)\sin x\,dx \end{eqnarray*} \]

Now we use the substitution \(u=\cos x\). Then \(du=-\sin x\,dx\), and \[ \begin{eqnarray*} \int \sin ^{5}x\,dx&=&-\int (1-2u^{2}+u^{4})~du=-u+\dfrac{2}{3}u^{3}-\dfrac{1}{5}u^{5}+C\\[3pt] &=&-\cos x+\dfrac{2}{3}\cos ^{3}x-\dfrac{1}{5}\cos ^{5}x+C \end{eqnarray*} \]

NOW WORK

Problem 3.

NEED TO REVIEW?

Trigonometric identities are discussed in Appendix A.4, pp. A-32 to A-35.

Finding the Integral \(\int \sin ^{2}x\,dx\)

Find \(\int \sin ^{2}x\,dx\).

Solution Since the exponent of \(\sin x\) is an even integer, we use the identity \[ \sin ^{2}x=\dfrac{1-\cos (2x) }{2} \]

Then \[ \begin{eqnarray*} \int \sin ^{2}x\,dx&=&\dfrac{1}{2}\int \,[ 1-\cos (2x) ] \,dx =\dfrac{1}{2}\int\, dx-\dfrac{1}{2}\int \cos (2x) \,dx \\[4pt] &=& \dfrac{1}{2} x + C_1 - \dfrac{1}{2} \int \cos u \dfrac{du}{2} \qquad {\color{#0066A7}{\hbox{\(u=2x, du=2\, dx\).}}} \\[4pt] &=& \dfrac{1}{2} x + C_1 - \dfrac{1}{4} \sin (2x) + C_2 \end{eqnarray*} \]

Since \(C_1\) and \(C_2\) are constants, we write the solution as \[ \int \sin^2 x \, dx =\dfrac{1}{2}x -\dfrac{1}{4} \sin (2x) +C \]

where \(C=C_1+C_2\).

NOTE

Usually we will just add the constant of integration at the end of the integration to avoid letting \(C=C_1+C_2\).

NOW WORK

Problem 5.

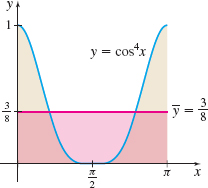
Finding the Average Value of a Function

Find the average value \(\bar{y}\) of the function \(f( x) =\cos ^{4}x\) over the closed interval \([0,\pi]\).

Solution The average value \(\bar{y}\) of a function \(f\) over \([a,b]\) is \(\bar{y}=\dfrac{1}{b-a}\int_{a}^{b}f(x)\,dx.\)

For \(f( x) =\cos ^{4}x\) on \([0,\pi]\), we have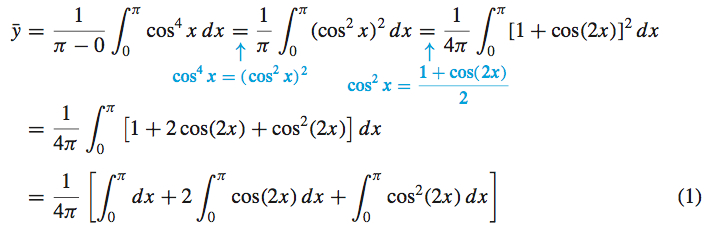

Now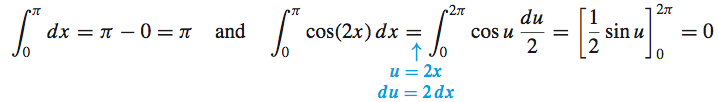

To find \(\int_{0}^{\pi }\cos ^{2}(2x)\, dx,\) we use the identity \( \cos ^{2}\theta =\dfrac{1+\cos (2\theta )}{2}\) again to write \(\cos ^{2}(2x) =\dfrac{1+\cos (4x) }{2}\). Then \[ \begin{eqnarray*} \int_{0}^{\pi }\cos ^{2}(2x) \,dx &=&\int_{0}^{\pi }\dfrac{ 1+\cos (4x) }{2}\,dx=\dfrac{1}{2}\left[ \int_{0}^{\pi }dx+\int_{0}^{\pi }\cos ( 4x) \,dx\right]\\[7pt] &=& \dfrac{1}{2}\left[ \pi +\int_{0}^{4\pi }\cos u\,\dfrac{du}{4}\right] \qquad {\color{#0066A7}{\hbox{\(u=4x\); \(du=4\,dx\)}}} \end{eqnarray*} \]

So, from (1), \[ \bar{y}=\dfrac{1}{4\pi }\left[ \pi +0+\dfrac{\pi }{2}\right] =\dfrac{3}{8} \]

NOW WORK

Problem 57.

Finding the Integral \(\int \sin ^{5}x\,\sqrt{\cos x}\,dx\)

Find \(\int \sin ^{5} x \sqrt{\cos x} dx = \int \sin^{5}x\,\cos ^{1/2}x\,dx\).

Solution The exponent of \(\sin x\) is \(5,\) a positive, odd integer. We factor \(\sin x\) from \(\sin ^{5}x\) and write \begin{align*} \int \sin ^{5} x\cos ^{1/2} x\,dx &= \int \sin ^{4} x\,\cos ^{1/2} x\sin x\,dx=\int(\sin ^{2}x) ^{2}\,\cos ^{1/2} x\sin x\,dx\\[4pt] &=\int ( 1-\cos ^{2}x) ^{2}\cos ^{1/2} x\sin xdx \end{align*}

Now we use the substitution \(u=\cos x.\) \[ \begin{eqnarray*} \int \sin ^{5}x\,\cos ^{1/2}x\,dx &=&\int (1-\cos ^{2}x) ^{2}\,\cos ^{1/2}x\,\sin x\,dx \nonumber \\ &\underset{\underset{\underset{\color{#0066A7}{\hbox{\(du=-\sin x~dx\)}}}{\color{#0066A7}{\hbox{\(u=\cos x\)}}}}{\color{#0066A7}{\uparrow }}}{=}&\int (1-u^{2})^{2}u^{1/2}(-du) \nonumber \\ &=&-\int (u^{1/2}-2u^{5/2}+u^{9/2})\,du=-\dfrac{2}{3}u^{3/2}+\dfrac{4}{7}u^{7/2}-\dfrac{2}{11}u^{11/2}+C \nonumber \\ &=&u^{3/2}\left[ -\dfrac{2}{3}+\dfrac{4}{7}u^{2}-\dfrac{2}{11}u^{4}\right] +C \nonumber \\ &\underset{\underset{\color{#0066A7}{\hbox{\(u=\cos x\)}}}{\color{#0066A7}{\uparrow }}}{=}&(\cos x) ^{3/2}\left[ -\dfrac{2}{3}+\dfrac{4}{7}\cos ^{2}x-\dfrac{2}{11}\cos ^{4}x\right] +C \end{eqnarray*} \]

NOW WORK

Problem 11.

Finding the Integral \(\int \tan ^{3}x\,\sec ^{4}x\,dx\)

Find \(\int \tan ^{3} x\sec ^{4} x\,dx\).

Solution Here, \(\tan x\) is raised to the odd power \(3.\) We factor \(\tan x\) from \(\tan ^{3}x\) and use the identity \(\tan ^{2} x=\sec^{2}x-1.\) \[ \begin{eqnarray*} \begin{array}{@rcl@l} \int \tan ^{3}x\sec ^{4}x\,dx &=& \int \tan ^{2}x\,\tan x\,\sec ^{4}x\,dx & {\color{#0066A7}{\hbox{Factor tan \(x\) from \(\tan^{3} x\).}}}\\[6pt] &=& \int (\sec ^{2}x-1) \tan x\sec ^{4}x\,dx & {\color{#0066A7}{\hbox{\(\tan^{2} x = \sec^{2} x - 1\)}}}\\[6pt] &=& \int ( \sec ^{2}x-1) \sec^{3}x\sec x\tan x\,dx & {\color{#0066A7}{\hbox{Factor sec \(x\) from \(\sec^{4} x\).}}}\\[6pt] &=& \int (u^{2}-1) u^{3}du & {\color{#0066A7}{\hbox{Substitute \(u=\sec x\);}}}\\[-4pt] &&& {\color{#0066A7}{\hbox{\(du = \sec x\) \(\tan x\,dx\).}}}\\[6pt] &=& \int (u^{5}-u^{3}) \,du =\dfrac{u^{6}}{6}-\dfrac{u^{4}}{4}+C \underset{\underset{\color{#0066A7}{\hbox{\(u=\sec x\)}}}{\color{#0066A7}{\uparrow}}}{=} \dfrac{\sec ^{6}x}{6}-\dfrac{\sec ^{4}x}{4}+C &\\[-13pt] \end{array} \end{eqnarray*} \]

NOW WORK

Problem 19.

Finding the Integral \(\int \tan ^{2}x\,\sec ^{4}x\,dx\)

Find \(\int \tan ^{2}x\sec ^{4}x\,dx.\)

Solution Here, \(\sec x\) is raised to a positive even power. We factor \(\sec ^{2}x\) from \(\sec ^{4}x\) and use the identity \(\sec ^{2}x=1+\tan ^{2}x.\) Then \[ \begin{eqnarray*} \begin{array}{rcl@l} \int \tan ^{2}x\sec ^{4}x\,dx &=&\int \tan ^{2}x\sec ^{2}x\cdot \sec ^{2}x\,dx & {\color{#0066A7}{\hbox{Factor \(\sec^2 x\) from \(\sec^4 x\).}}} \\[5pt] &=&\int \tan ^{2}x(1+\tan ^{2}x)\sec ^{2}x\,dx & {\color{#0066A7}{\hbox{\(\sec ^{2}{x=1+}\tan ^{2}{x}\)}}} \nonumber \\[5pt] &=&\int u^{2}(1+u^{2})\,du & {\color{#0066A7}{\hbox{Substitute \(u=\tan x\);}}} \nonumber \\[0pt] &&&{\color{#0066A7}{\hbox{\(du=\sec ^{2} x\,dx\).}}}\nonumber \\[5pt] &=&\int (u^{2}+u^{4})\,du = \dfrac{u^{3}}{3}+\frac{u^{5}}{5}+C \underset{\underset{\color{#0066A7}{\hbox{\(u=\tan x\)}}}{\color{#0066A7}{\uparrow}}}{=}\dfrac{\tan ^{3}x}{3}+\dfrac{\tan ^{5}x}{5}+C\\[-8pt] \end{array} \end{eqnarray*} \]

NOW WORK

Problem 21.

Finding the Integral \(\int \tan ^{2}x\,\sec x\,dx\).

Find \(\int \tan ^{2}x\sec x\,dx\).

Solution Here, tan \(x\) is raised to an even power and sec \(x\) to an odd power. We use the identity \(\tan ^{2}x=\sec ^{2}x-1\) to write \[ \begin{eqnarray*} \int \tan ^{2}x\sec x\,dx &=&\int (\sec ^{2}x-1)\sec x\,dx=\int ( \sec ^{3}x-\sec x)~dx\nonumber\\[4pt] &=&\int \sec ^{3}x\,dx-\int \sec x\,dx\tag{2} \end{eqnarray*} \]

Next we integrate \(\int \sec ^{3}x\,dx\) by parts. Choose \[ \begin{array}{rcl@{\qquad}c@{\qquad}rcl} u &=&\sec x &\hbox{and}& dv &=&\sec ^{2}x\,dx \\[3pt] du &=&\sec x\tan x\,dx &\hbox{}& v &=&\int \sec ^{2}x\,dx=\tan x \end{array} \]

Then \[ \begin{array}{@rcl@{\quad}l} \int \sec ^{3}x\,dx &=&\sec x\,\tan x-\int \tan ^{2}x\,\sec x\,dx & {\color{#0066A7}{\int udv = uv-\int vdu}}\\ &=&\sec x\,\tan x-\int ( \sec ^{2}x-1) \,\sec x\,dx & {\color{#0066A7}{\hbox{\(\tan ^{2}{x=}\sec ^{2}{x-1}\)}}} \\ &=&\sec x\,\tan x-\int \sec ^{3}x\,dx+\int \sec x\,dx & {\color{#0066A7}{\hbox{Write the integral as the}}} \\ &&& {\color{#0066A7}{\hbox{sum of two integrals.}}} \\ 2\int \sec ^{3}x\,dx &=&\sec x\,\tan x+\int \sec x\,dx & {\color{#0066A7}{\hbox{Add \(\int \sec ^{3}x~dx\) to both sides.}}} \\ \int \sec ^{3}x\,dx &=&\dfrac{1}{2}[ \sec x\,\tan x+\ln \vert \sec x+\tan x\vert ] & {\color{#0066A7}{\hbox{Solve for \(\int \sec ^{3}x~dx\);} }}\\ &&&{\color{#0066A7}{\hbox{\(\int \sec x~dx=\ln \left\vert \sec {x+}\tan {x}\right\vert\).}}} \end{array} \]

Now we substitute this result in (2). \[ \begin{eqnarray*} \int \tan ^{2}x\sec x\,dx &=&\int \sec ^{3}x\,dx-\int \sec x\,dx\\[4pt] &=& \dfrac{1}{2}\left[ \sec x\,\tan x+\ln \vert \sec x+\tan x\vert \right] -\ln \vert \sec x+\tan x\vert +C \nonumber \\[4pt] &=&\dfrac{1}{2}\left[ \sec x\tan x-\ln \,\vert \sec x+\tan x\vert \right] +C \end{eqnarray*} \]

NOTE

Substituting \(n = 3\) into the reduction formula for \(\int \sec ^{n} x\,dx\) (derived in Example 8 of Section 7.1) could also have been used to find \(\int \sec ^{3} x\,dx.\)

NOW WORK

Problem 23.

• \(2\sin A\sin B=\cos (A-B)-\cos (A+B)\)
• \(2\sin A\cos B=\sin (A+B)+\sin (A-B)\)
• \(2\cos A\cos B=\cos (A-B)+\cos (A+B)\)

Finding the Integral \(\int \sin (3x) \sin (2x) \,dx\)

Find \(\int \sin (3x) \sin (2x) \,dx\).

Solution We use the product-to-sum identity \(2\sin A\sin B=\cos(A-B)-\cos (A+B).\)

Then \[ \begin{eqnarray*} 2\sin (3x) \sin (2x) &=&\cos (3x-2x) -\cos (3x+2x) \\[4pt] \sin (3x) \sin (2x) &=&\dfrac{1}{2}[ \cos x-\cos (5x) ] \end{eqnarray*} \]

Then \[ \begin{eqnarray*} \int \sin (3x) \sin (2x) \,dx&=&\dfrac{1}{2}\int [\cos x-\cos (5x) ] \,dx=\dfrac{1}{2}\int \cos x~dx-\dfrac{1}{2}\int \cos (5x) \,dx\\[5pt] &&\underset{\underset{\underset{\color{#0066A7}{\hbox{\(du=5~dx\)}}}{\color{#0066A7}{\hbox{\(u=5x\)}}}}{\color{#0066A7}{\uparrow }}}{=} \dfrac{1}{2}\sin x-\dfrac{1}{2}\int \cos u\,\dfrac{du}{5}=\dfrac{1}{2}\sin x-\dfrac{1}{10}\sin (5x) +C \end{eqnarray*} \]

NOW WORK

Problem 27.