Chapter 11Printed Page AN-52
1. {t | t ≤ 4}
2. False
3. True
4. True
5. False
6. u′ × v+u × v′
7. i − 2j
9. 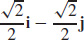
11. i−2k
13. 4i + j +8k
15. All real numbers
17. {t|t ≥ 0}
19. {t|t ≠ 0}
21. {t|t > 0}
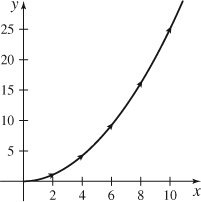
23. 
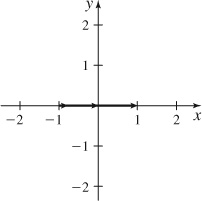
25. 
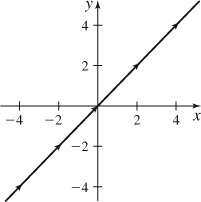
27. 
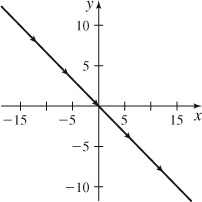
29. 
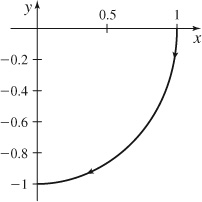
31. 
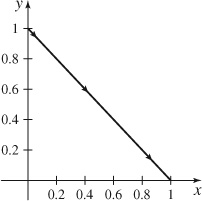
33. 
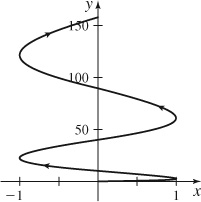
35. 
37. D
39. C
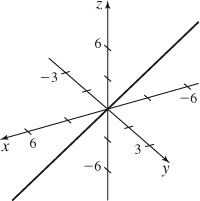
41. 
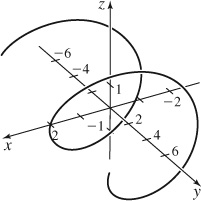
43. 
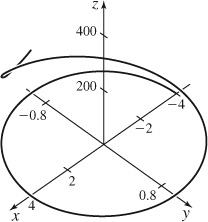
45. 
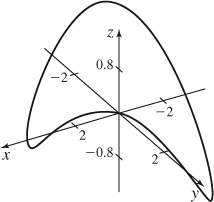
47. 
49. {t|t ≠ −1, 1}
51. 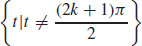
53. {t|t ≠ −1}
55. 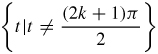
57. r′ (t) = 8ti − 6t2j and r″(t) = 8i − 12tj
59.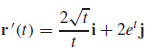 and
and 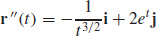
61. r′ (t) = j + 2tk and r″(t) = 2k
63. r′(t) = 2ti + 3t2j − k and r″(t) = 2i + 6tj
65. r′ (t) = sin(2t)i+sin(2t)j and r″(t) = 2 cos(2t)i+2 cos(2t)j
67. 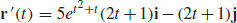 and
and 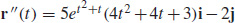
69. r′ (t) = (et cos t − et sin t)i + (et sin t + et cos t)j + k and r″(t) = −2et sin ti + 2et cos tj
71. r′ (t) = (1 − 3t2)i + (1 + 3t2)j − k and r″ (t) = −6ti + 6tj
73. 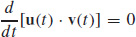
75. 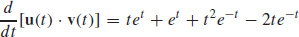
77. 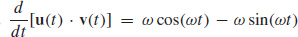
79. 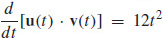 and
and 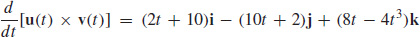
81. 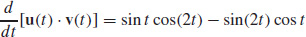 and
and 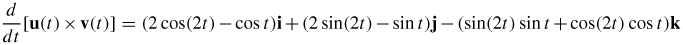
83. 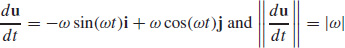
85. See Student Solutions Manual.
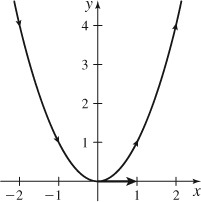
87. 
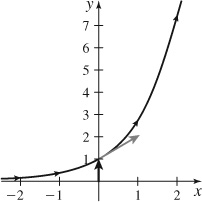
89. 
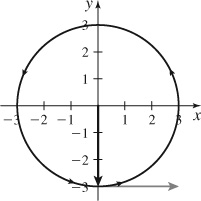
91. 
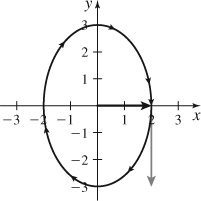
93. 
95. (a) y = 1 − x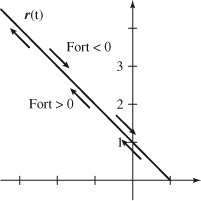
97. (a) 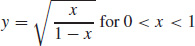
(b) 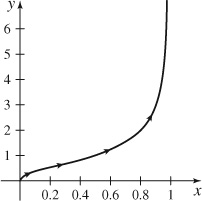
99. See Student Solutions Manual.
101. See Student Solutions Manual.
103. Answers will vary.
105. See Student Solutions Manual.
107. See Student Solutions Manual.
1. False
2. False
3. False
4. False
5. True
6. True
7.
(a) r′(1) = i − 2j
(b) and
(c) 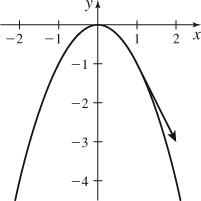
9.
(a) r′ (1) = 2i − j
(b) and
(c) 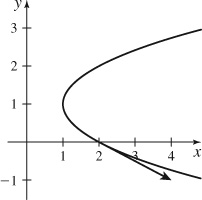
11. (a)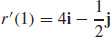
(b) and
(c) 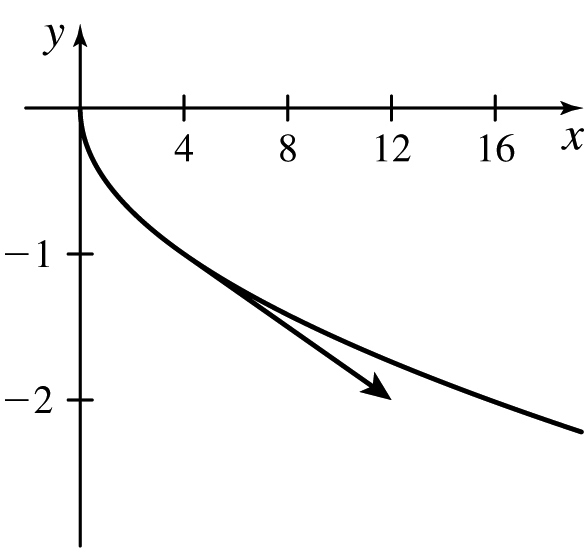
13.
(a) r′ (0) = i − j
(b) and
(c) 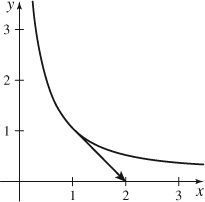
15. r′ (0) = −3i + 2j − k
17. 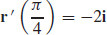
19. 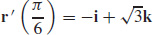
21. r′ (0) = i + j + k
23. Figure below not drawn to scale.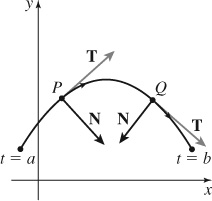
25. Figure below not drawn to scale.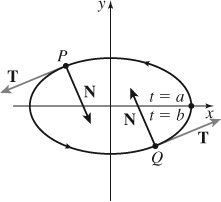
27. 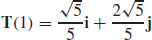 and
and 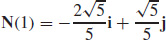
29. 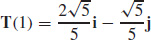 and
and 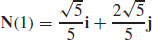
31. 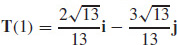 and
and 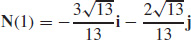
33. 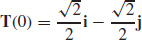 and
and 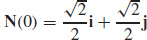
35. 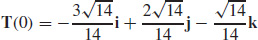 and N(0) is undefined
and N(0) is undefined
37. 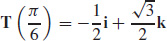 and
and 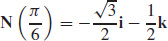
39. 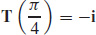 and
and 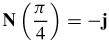
41. 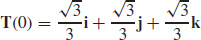 and \({\rm {\bf N}}(0) = -\dfrac{\sqrt{2}}{2}{\rm {\bf i}} +\dfrac{\sqrt{2}}{2}{\rm {\bf j}}\)
and \({\rm {\bf N}}(0) = -\dfrac{\sqrt{2}}{2}{\rm {\bf i}} +\dfrac{\sqrt{2}}{2}{\rm {\bf j}}\)
43. s = 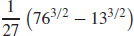
45. s = 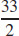
47. s = 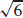
49. s = 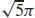
51. s = 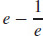
53. s = 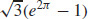
55. (a) 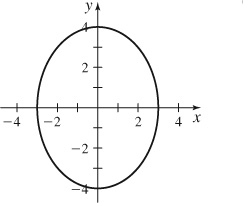
(b) s ≈ 11.052
57. (a) 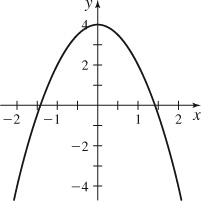
(b) s ≈ 33.637
59. 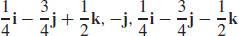
61. θ ≈ 37°
63. 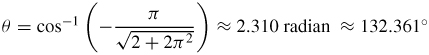
65. θ = 90°
67. 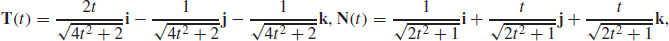 and
and 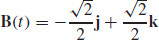
69. 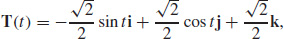 N (t) = −cos ti − sin tj, and
N (t) = −cos ti − sin tj, and 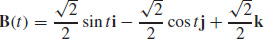
71. 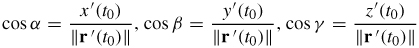
73. s ≈ 10.516
75. (a) s = 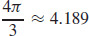
(b) s ≈ 33.510
(c) See the Student Solutions Manual
1. (d)
2. False
3. False
4. True
5. False
6. 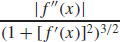
7. 
8. False
9. No
11. No
13. No
15. Yes
17. No
19. P R Q
21. κ = 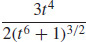
23. κ = 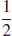
25. κ = 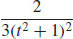
27. κ = 0
29. κ = 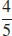
31. κ = 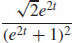
33. κ = 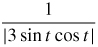
35. κ = 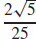
37. κ = 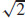
39. κ = 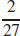
41.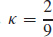
43.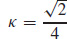
45. ρ = 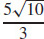
47. ρ = 1
49. ρ = 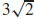
51. ρ = 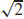
53. ρ = 6
55. ρ = 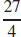
57. ρ = 
59. ρ = 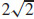
61. ρ = 12a
63. See the Student Solutions Manual.
65. 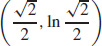
67. \(\left(\pm\left(\dfrac{1}{5}\right)^{{1}/{4}},\;\pm\dfrac{1}{3}\left(\dfrac{1}{5}\right)^{{3}/{4}}\right)\)
69. α = 1
71. See the Student Solutions Manual.
73. κ = 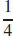
75. κ = 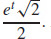 As t →∞, κ → ∞ as the graph curves more and more tightly around the origin.
As t →∞, κ → ∞ as the graph curves more and more tightly around the origin.
77. See the Student Solutions Manual.
79. 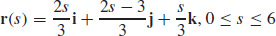
81. See the Student Solutions Manual.
83. See the Student Solutions Manual.
85. See the Student Solutions Manual.
87. \(\kappa=\dfrac{\sqrt{2}}{2}\), \(\mathbf{T}(s)=\dfrac{\sqrt{2}}{2}\cos{s}\mathbf{i}-\dfrac{\sqrt{2}}{2}\sin{s}\mathbf{j}+\dfrac{\sqrt{2}}{2}\mathbf{k}\), \(\mathbf{N}(s)=-\sin{s}\mathbf{i}-\cos{s}\mathbf{j}\), and \(\mathbf{B}(s)=\dfrac{\sqrt{2}}{2}\cos{s}\mathbf{i}-\dfrac{\sqrt{2}}{2}\sin{s}\mathbf{j}-\dfrac{\sqrt{2}}{2}\mathbf{k}\)
89. κ = 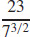
91. κ = 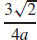
93. κ = 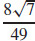
95. See the Student Solutions Manual.
97. 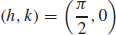
99. 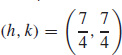
101. See the Student Solutions Manual.
1. True
2. False
3. True
4. Tangential, normal
5. (a) v(t) = i + 2tj, a(t) = 2j, and 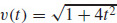
(b) 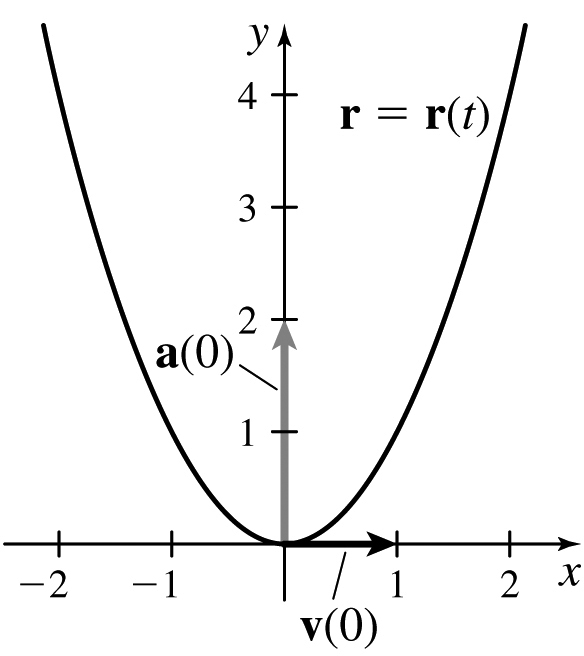
7. (a) v (t) = 2ti − j, a(t) = 2i, and 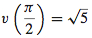
(b) 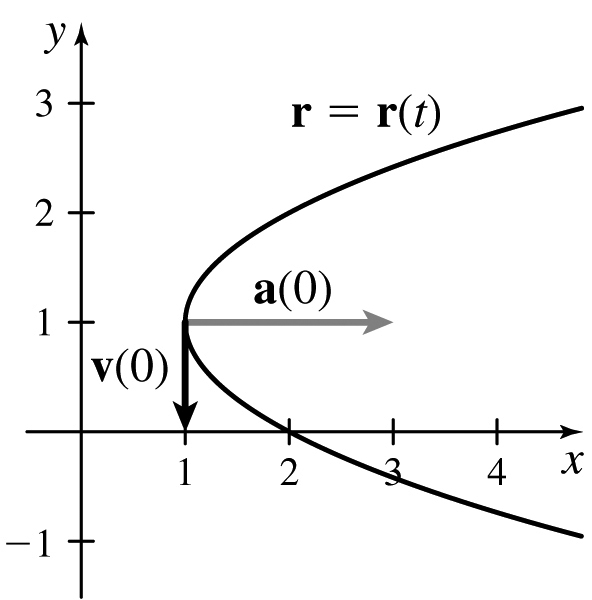
9. (a) v(t) = 4i + 3t2j, a(t) = 6tj, and 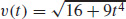
(b) 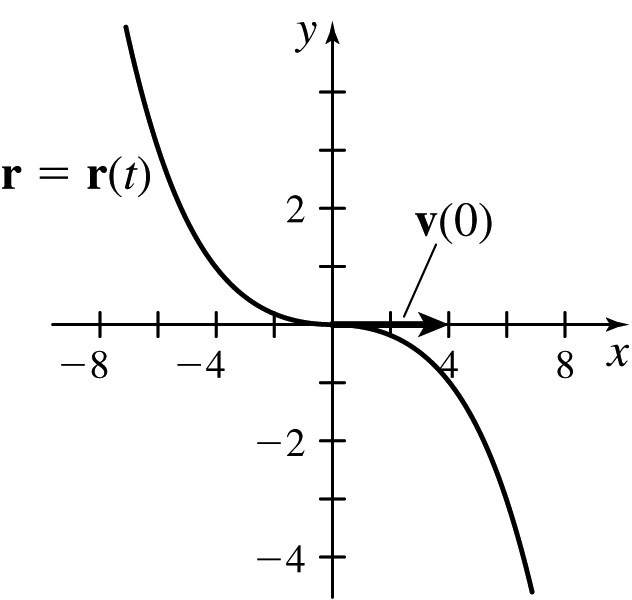
11. v (t) = 2ti + j − 9t2k, a(t) = 2i − 18tk, and 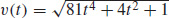
13. 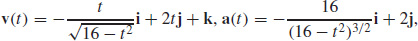 and
and 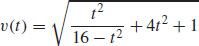
15. v (t) = −2 sin ti + cos tj + k, a(t) = −2 cos ti − sin tj, and 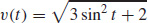
17. (a) v (t) = costi − sin tj + 2 cos(2t)k, a(t) = −sin ti − cos tj − 4 sin(2t)k,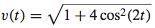
(b) 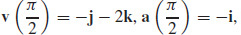 and
and 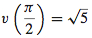
(c) 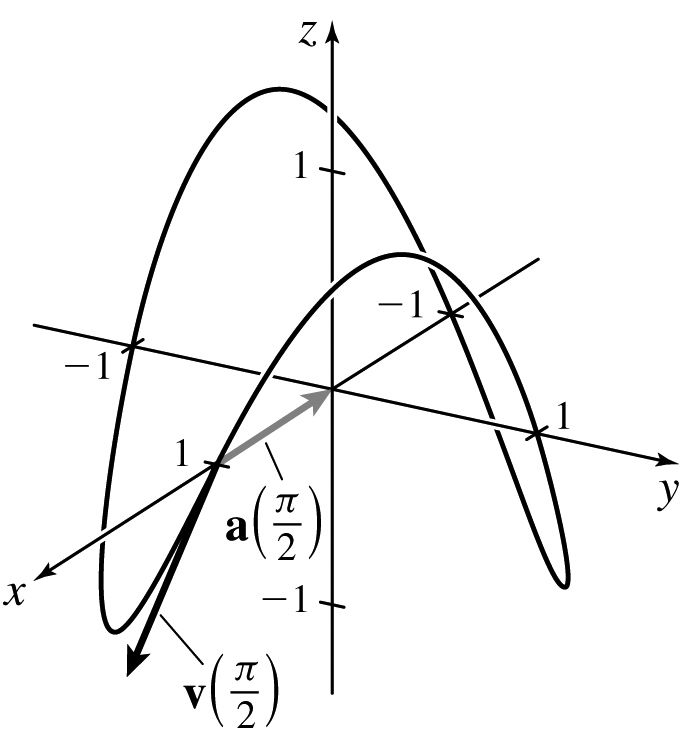
19. (a) F(t) = mr(t)
(b) 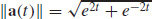
21. (a) F(t) = m et j
(b) 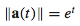
23. (a) F(t) = −4mr(t)
(b) 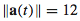
25. (a) F(t) = −mr(t)
(b) 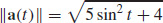
27. (a) v(t) = 2i + j, a(t) = 0, and 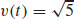
(b) aT = 0, aN = 0
29. (a) v(t) = eti + 2e2tj, a(t) = eti + 4e2tj, and 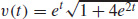
(b) 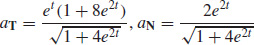
31. (a) v(t) = 2 cos ti − sin tj, a(t) = −2 sin ti − cos tj, and 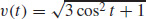
(b) 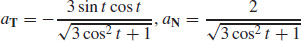
33. (a) v (t) = −3i + 2j − k, a (t) = 0, and 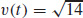
(b) aT = 0, aN = 0
35. (a) v (t) = i + 2tj + 3t2k, a(t) = 2j + 6tk, and 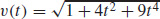
(b) 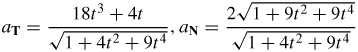
37. (a) v (t) = −sin tj + cos tk, a (t) = −cos tj − sin tk, and ν(t) = 1
(b) aT = 0, aN = 1
39. (a) 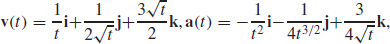 and
and 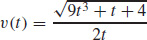
(b) 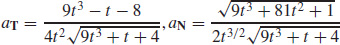
41. (a) v (t) = (et cos t − et sin t)i + (et sin t + et cos t)j + etk, a(t) = −2et sin ti + 2et cos tj + etk, and 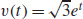
(b) 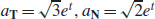
43. (a) v(t) = −a sin ti + b cos tj + ck, a(t) = −a cos ti − b sin tj, and 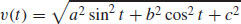
(b) 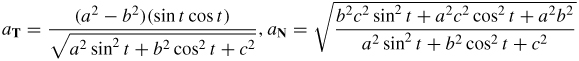
45. v(t) = (π − π cos(πt))i + π sin(πt)j, a(t) = π2 sin(πt)i + π2 cos(πt)j
47. 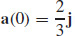 and
and 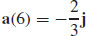
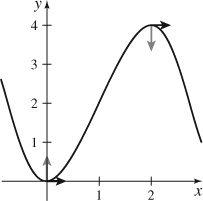
49. See the Student Solutions Manual.
51. aT = 0 and 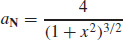
53. (a) 350 N
(b) 35 km/h slower
55. 2.118 × 1013m N
57. \(4\sqrt{5}\;m\)
59. (a)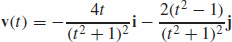
(b) No
(c) (−1, 0)
61. (a) See the Student Solutions Manual.
(b) 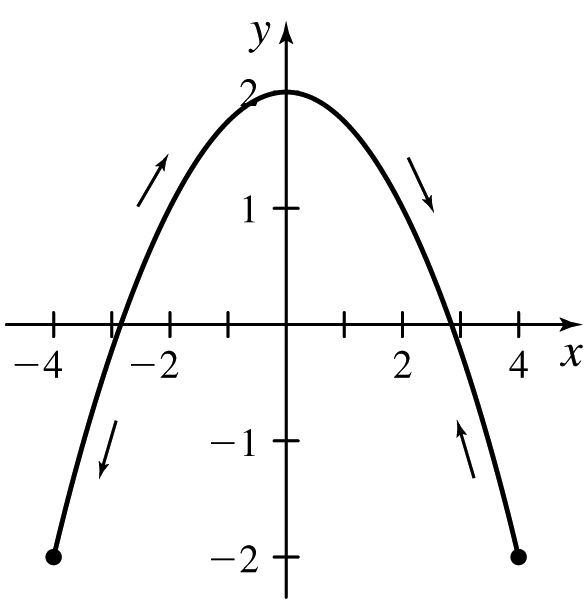
(c) 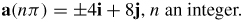
63. ν ≈ 3750 m/s
65. See Student Solutions Manual.
67. See Student Solutions Manual.
69. Answers will vary.
71. See Student Solutions Manual.
73.
(a) v(t) = 2t cos(ωt)i + 2t sin(ωt)j + t2vd and a(t) = 2 cos(ωt)i + 2 sin(ωt)j + 4tvd + t2ad
(b) 2 cos(ωt)i + 2 sin(ωt)j + 4tvd
75. See Student Solutions Manual.
77. r = e2t, where θ = t; v(t) = 2rur + ruθ; a(t) = 3rur + 4ruθ
1. True
2. False
3. 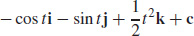
5. 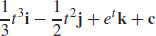
7. 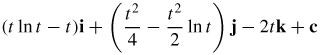
9. 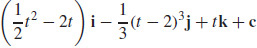
11. r(t) = (et − e)i + (t − t ln t)j + t2k
13. r(t) = (3 − 2 cos t)i + (sin t − 1)j + tk
15. r(t) = 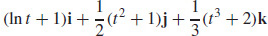
17. v(t) = −32tk, υ(t) = 32t, and r(t) = −16t2k
19. v(t) = (sin t + 1)i + (1 − cos t)j, v (t) =  and r (t) = (t − cos t + 1)i + (t − sin t + 1)j
and r (t) = (t − cos t + 1)i + (t − sin t + 1)j
21. v(t) = i − 9.8tk, v (t) =  and r(t) = ti + (5 − 4.9t2)k
and r(t) = ti + (5 − 4.9t2)k
23. v(t) = (2 − e−t)i + (t + 1)j, v (t) = 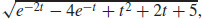 and r (t) =
and r (t) = 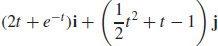
25. The range ≈ 23,895 m, the time of flight ≈ 53 s, and the greatest height reached ≈3449 m.
27. (a) x = 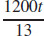 and y =
and y = 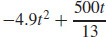
(b) Range ≈ 724.6 m
(c) Time of flight ≈ 7.8 s
(d) 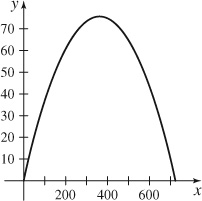
29. (a) The projectile travels approximately 152.5 feet up the hill.
(b) The projectile is in the air for approximately 1.9 seconds.
31. (a) v(t) = 5ti + (−9.8t + 3)j and v(t) = 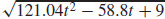
(b) r(t) = 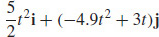
(c) ≈0.612 s
(d) 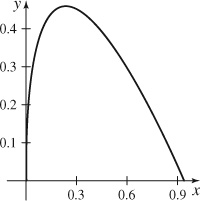
33. v0 ≈ 54.521 ft/s
35. The initial speed of the ball is approximately 114 ft/s. It took the ball approximately 5 s to reach the vines.
37. (a) Range ≈ 114.342 ft
(b) ≈93 ft
39. See Student Solutions Manual.
41. See Student Solutions Manual.
43. See Student Solutions Manual.
45. See Student Solutions Manual.
1. ≈79.479 days
3. Answers will vary.
5. (a)See Student Solutions Manual.
(b) M ≈ 2.0 × 1030kg
7. See Student Solutions Manual.
1. (a) All real numbers.
(b) 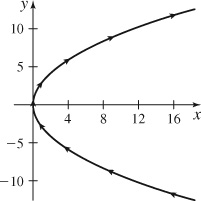
(c) r′(2) = 4i + 3j
3. (a) All real numbers.
(b) 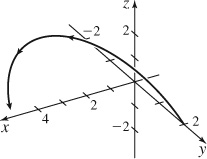
(c) r′(0) = i + 2k
5. 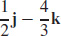
7. Continuous
9. r′ (t) = −2 sin ti − 3 sin tj + k and r″ (t) = −2 cos ti − 3 cos tj
11. [f(t) · g(t)]′ = 4t − 2 sin(2t) cos t − cos(2t) sin t − 5 cos t and
[f(t) × g(t)]′ = (−2 sin(2t) sin t + cos(2t) cos t − 5 sin t)i + (−10 − sin t − t cos t)j + (cos t − t sin t + 4t sin(2t) − 2 cos(2t))k
13.
(a) r′(0) = i + 2j
(b)T (0) = 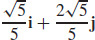
(c) N(0) = −k
15. 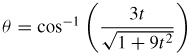
17. 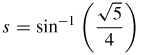
19. No
21. 
23. κ = 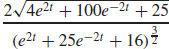
25. κ = 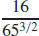
27. ρ = ∞
29. κ = 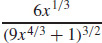
31.
(a) v(t) = −2 sin ti + cos tj, a(t) = −2 cos ti − sin tj, and v(t) = 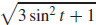
(b) 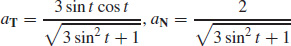
33.
(a) v(t) = eti − e−tj, a(t) = et i + e−t j, and v(t) = 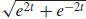
(b)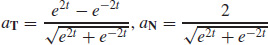
35. v(t) = (π − cos(πt))i + π sin(πt)j and a(t) = π2 sin(πt)i + π2 cos(πt)j
37. 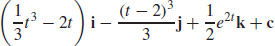
39. 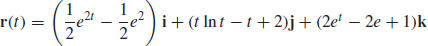
41. 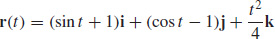
43. ≈25,540 m away