Section 3.5 Exercises

CLARIFYING THE CONCEPTS

Question 3.376

1. True or false: The five-number summary consists of the minimum, Q1, Mean, Q3, Maximum. (p. 172)

3.5.1

False

Question 3.377

2. Explain what we mean when we say that the five-number summary is associated with the boxplot. (p. 173)

Question 3.378

3. Explain how we can use a boxplot to recognize the following:

  1. Symmetric distribution (p. 176)
  2. Right-skewed distribution (p. 175)
  3. Left-skewed distribution (p. 176)

3.5.3

(a) The median will be about the same distance from Q1 and Q3, and the upper and lower whiskers will be about the same length. (b) The median is closer to Q1 than to Q3, and the upper whisker is much longer than the lower whisker. (c) The median is closer to Q3 than to Q1, and the lower whisker is much longer than the upper whisker.

Question 3.379

4. When is it possible for outliers to be found inside the box of a boxplot? (p. 177)

Question 3.380

5. Explain the IQR method for detecting outliers. (p. 177)

3.5.5

Any data value located 1.5 (IQR) or more below Q1 or 1.5 (IQR) or more above Q3 is considered an outlier.

Question 3.381

6. Why do we need the IQR method for detecting outliers when we already have the -score method? (p. 177)

PRACTICING THE TECHNIQUES

image CHECK IT OUT!

To do Check out Topic
Exercises 7–8,
13–14, and 19–20.		 Example 31 Five-number summary
Exercises 9–10,
15–16, and 21–22.		 Example 34 Boxplots
Exercises 11–12,
17–18, and 23–24.		 Example 37 IQR method for
identifying outliers
Exercises 25 and 26 Examples 35
and 36 		Boxplots and
skewness
Exercises 27–30 Example 38 Comparison boxplots

Use the following cell phone price data for Exercises 7–12.

Samsung Galaxy S5 Standard $200
Samsung Galaxy S5 Active $200
Sony Xperia Z2 $600
Nokia Lumia Icon $200
LG G3 $800
Apple iPhone 5s $250
HTC One M8 $200
Samsung Galaxy Note 3 $300
Table 3.101: Source: www.cnet.com/topics/phones/best-phones.

Question 3.382

7. Find the quartiles.

3.5.7

Q1 = $200, Q2 = median = $225, Q3 = $450

Question 3.383

8. Compute the five-number summary.

Question 3.384

9. Calculate the interquartile range for cell phone price.

3.5.9

$250

Question 3.385

10. Construct a boxplot for cell phone price.

Question 3.386

11. Use the IQR method to determine whether $200 is an outlier.

3.5.11

No

Question 3.387

12. Use the IQR method to determine whether $600 is an outlier.

The Environmental Protection Agency calculates the estimated annual fuel cost for motor vehicles, with the resulting data provided in the variable annual fuel cost of the Chapter 8 Case Study data set FuelEfficiency. A sample of the annual fuel cost (in dollars) is provided for 12 vehicles. Use this data to answer Exercises 13–18.

Annual fuel cost (dollars)
1750 2500 2400 2350
2150 3100 2950 2500
2550 2750 2300 2800

Question 3.388

13. Find the quartiles.

3.5.13

Q1 = 2325, Q2 = Median = 2500, Q3 = 2775

Question 3.389

14. Compute the five-number summary.

181

Question 3.390

15. Calculate the interquartile range for annual fuel cost.

3.5.15

450

Question 3.391

16. Construct a boxplot for annual fuel cost.

Question 3.392

17. Use the IQR method to determine whether $1750 is an outlier.

3.5.17

No

Question 3.393

18. Use the IQR method to determine whether $3100 is an outlier.

Here are the numbers of criminal trespass cases for the police precincts in Brooklyn in 2013. Use this data set to answer Exercises 19–24.

Criminal trespass cases
150 451
98 111
55 166
41 67
68 258
101 190
32 145
101 49
88 131
55 223
111 48
363

Question 3.394

19. Find the quartiles.

3.5.19

Q1 = 55, Q2 = median = 101, Q3 = 166

Question 3.395

20. Compute the five-number summary.

Question 3.396

21. Calculate the interquartile range.

3.5.21

111

Question 3.397

22. Construct a boxplot for the number of criminal trespass cases.

Question 3.398

23. Use the IQR method to determine whether 32 criminal trespass cases is an outlier.

3.5.23

Not an outlier

Question 3.399

24. Use the IQR method to determine whether 451 criminal trespass cases is an outlier.

For Exercises 25 and 26, do the following:

  1. Identify the shape of the distribution.
  2. Use the boxplot to find the five-number summary.

Question 3.400

25.

image

3.5.25

(a) Right-skewed (b) Minimum = 0, Q1 = 1, Q2 = median = 3, Q3 = 7.5, maximum = 12

Question 3.401

26.

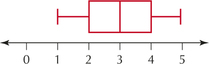
image

Use the comparison boxplots shown to answer Exercises 27–30.

image

Question 3.402

27. For the variable :

  1. Identify the shape of the distribution.
  2. Use the boxplot to find the five-number summary.

3.5.27

(a) Right-skewed (b) Minimum = 5, Q1 = 10, Q2 = median = 15, Q3 = 25, maximum = 45

Question 3.403

28. For the variable :

  1. Identify the shape of the distribution.
  2. Use the boxplot to find the five-number summary.

Question 3.404

29. Which variable has greater variability, according to the IQR?

3.5.29

Question 3.405

30. Which variable has greater variability, according to the range?

APPLYING THE CONCEPTS

Most active Stocks. Use Table 28 for Exercises 31–38. These companies represent the 10 most actively traded stocks on the NASDAQ stock exchange as of 10:00 A.M. on July 11, 2014. The variables are the stock price and the net change in stock price, with both variables in dollars.

Table 3.104: Table 28 The most active stocks on NA SDAQ
Company Price Change
Facebook 65.28 +0.41
Apple 95.18 +0.15
Cisco Systems 25.28 +0.14
Intel 31.25 −0.01
Fifth Street Finance 9.66 −0.36
QQQQ Trust 94.75 +0.09
Microsoft 41.54 −0.15
Sirius XM 3.38 −0.01
eBay 51.43 +1.09
Yahoo 35.02 +0.09
Table 3.104: Source: www.nasdaq.com.

Question 3.406

nasdaqstock

31. Find the five-number summary for price.

3.5.31

Minimum = 3.38, Q1 = 25.28, Q2 = median = 38.28, Q3 = 65.28, Maximum = 95.18

Question 3.407

nasdaqstock

32. Find the interquartile range for price. Interpret what this value means.

Question 3.408

nasdaqstock

33. Use the IQR method to investigate the presence of outliers in price.

3.5.33

No outliers.

Question 3.409

nasdaqstock

34. Construct a boxplot for price.

Question 3.410

nasdaqstock

35. Find the five-number summary for change.

3.5.35

Minimum = −0.36, Q1 = −0.01, Q2 = median = 0.09, Q3 = 0.15, Maximum = 1.09

Question 3.411

nasdaqstock

36. Find the interquartile range for change. Interpret what this value means.

Question 3.412

nasdaqstock

37. Use the IQR method to investigate the presence of outliers in change.

3.5.37

–0.36, 0.41, and 1.09 are outliers.

Question 3.413

nasdaqstock

38. Construct a boxplot for change.

Dietary Supplements. Refer to Table 24 (page 170) for Exercises 39–44.

Question 3.414

dietarysupp

39. Find the five-number summary for usage.

3.5.39

Min = 2,000,000; Q1 = 2,800,000; median = 4,200,000; Q3 = 7,100,000; max = 14,700,000

Question 3.415

dietarysupp

40. Find the interquartile range for usage. Interpret what this value actually means, so that a nonspecialist could understand it.

Question 3.416

dietarysupp

41. Use the IQR method to investigate the presence of outliers in usage.

3.5.41

Q1 – 1.5 * IQR = −3.65 and Q3 + 1.5 * IQR = 13.55. Usage of 14,700,000 is the only outlier.

Question 3.417

dietarysupp

42. Construct a boxplot for usage.

Question 3.418

dietarysupp

43. Calculate the mean and standard deviation of usage.

3.5.43

Mean: 5,073,300; standard deviation: 3,359,300

Question 3.419

dietarysupp

44. Find the -score for echinacea, and use it to determine whether the product is an outlier. Compare the result with that from the IQR method.

BRINGING IT ALL TOGETHER

Honda or Lexus? The following data represent the combined (city and highway) fuel efficiency in miles per gallon for independent random samples of models manufactured by Honda and Lexus. Use this data for Exercises 45–53.

182

Honda car mpg Lexus car mpg
Accord 24 GX 470 15
Odyssey 18 LS 460 18
Civic Hybrid 42 RX 350 19
Fit 31 IS 350 20
CR-V 23 GS 450 23
Ridgeline 17 IS 250 24
S2000 21

Question 3.420

hondalexus

45. Compute the five-number summary for each of the Honda cars and the Lexus cars.

3.5.45

Honda: Minimum = 17, Q1 = 18, Q2 = median = 23, Q3 = 31, Maximum = 42; Lexus: Minimum = 15, Q1 = 18, Q2 = median = 19.5, Q3 = 23, Maximum = 24

Question 3.421

hondalexus

46. Construct comparison boxplots for the Honda cars and the Lexus cars.

Question 3.422

hondalexus

47. Describe the shapes of the distribution for the Honda cars and the Lexus cars.

3.5.47

The distribution of the mpg for the Honda cars is right-skewed. The distribution for the mpg for the Lexus cars is right-skewed.

Question 3.423

hondalexus

48. Based on your descriptions in the previous exercise, would you expect the mean to be larger or smaller or about the same as the median for the Honda cars? The Lexus cars?

Question 3.424

hondalexus

49. Calculate the mean for the Honda cars and the Lexus cars. Do they concur with your expectations from the previous exercise?

3.5.49

Honda: Mean = 25.14 mpg; Lexus: Mean = 19.83 mpg. Yes

Question 3.425

hondalexus

50. Describe the difference between the Honda cars and the Lexus cars, in terms of the location of the box. Which make of vehicle seems to have the greater overall combined mpg? Does this agree with what a comparison of the means from the previous exercise is telling you?

Question 3.426

hondalexus

51. Describe the difference of the combined mpg between the Honda cars and the Lexus cars, in terms of the IQR measure of spread.

3.5.51

Honda: IQR = 13 mpg; Lexus: IQR = 5 mpg. The IQR for the Honda cars is larger than the IQR for the Lexus cars. This indicates that the data for the Honda cars has a larger spread than the data for the Lexus cars.

Question 3.427

hondalexus

52. Based on your answer to the previous exercise, which make of car has greater variability?

Question 3.428

hondalexus

53. Identify any outliers for the Honda cars and the Lexus cars, using the IQR method.

3.5.53

No outliers in either group.

WORKING WITH LARGE DATA SETS

Nutrition. Use the data set Nutrition for Exercises 54–57.

Question 3.429

nutrition

54. Open the data set nutrition.

  1. How many observations are in the data set?
  2. How many variables?

Question 3.430

nutrition

55. Use a statistical computing package (like Minitab) to explore the variable iron.

  1. Find the mean and standard deviation for the amount of iron in the food.
  2. Find the five-number summary the range, and the interquartile range.

3.5.55

Mean = 1.784 mg, standard deviation = 3.138 mg, min = 0.000 mg, Q1 = 0.300 mg, median = 0.800 mg, Q3 = 1.700 mg, max = 37.600 mg. Range = 37.600 mg – 0.000 mg = 37.600 mg. IQR = 1.700 mg – 0.300 mg = 1.400 mg

Question 3.431

nutrition

56. Which food item has the maximum amount of iron? Does this surprise you?

Question 3.432

nutrition

57. Use the computer to generate a boxplot. Also, comment on the symmetry or the skewness of the boxplot.

3.5.57

The boxplot is very right-skewed.

WORKING WITH LARGE DATA SETS

image Financial Experts versus the Darts. This set of exercises uses the Darts data set from the Chapter 3 Case Study to examine the methods and techniques we have learned in this section. Open the Darts data set. Use technology to do the following in Exercises 58–63.

Question 3.433

darts

58. Find the five-number summary for each group.

Question 3.434

darts

59. Construct a comparison boxplot of all three groups. From the boxplot, which group has the greatest variability? The smallest variability?

3.5.59

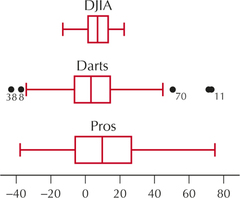
image

Pros has the greatest variability, DJIA has the smallest.

Question 3.435

darts

60. Calculate the range and standard deviation for each group. Does the relative variability of the groups agree with your answer from Exercise 59?

Question 3.436

darts

61. For which groups are there no outliers?

3.5.61

Pros and DJIA

Question 3.437

darts

62. How many outliers are there for the Darts? Verify using the IQR method that these data values are indeed outliers.

Question 3.438

darts

63. Check whether the outliers you found in Exercise 62 are also identified as outliers using the -score method.

3.5.63

image

for

Moderately unusual

for

Moderately unusual

for

Outlier

for

Outlier

for

Moderately unusual