2-6 Telescopes use lenses, mirrors, and electronics to concentrate and capture incoming light for study
Understanding what information is carried by light is only half the challenge of the enterprise of astronomy. The other half involves capturing this light so it can be decoded. In this section we will first cover the basic properties and functions of telescopes, as well as the new technologies that have moved us forward. Next, we will cover the telescopes in space. We will conclude with a discussion of the advances in our technological abilities to capture and record light.
Telescopes Gather Light
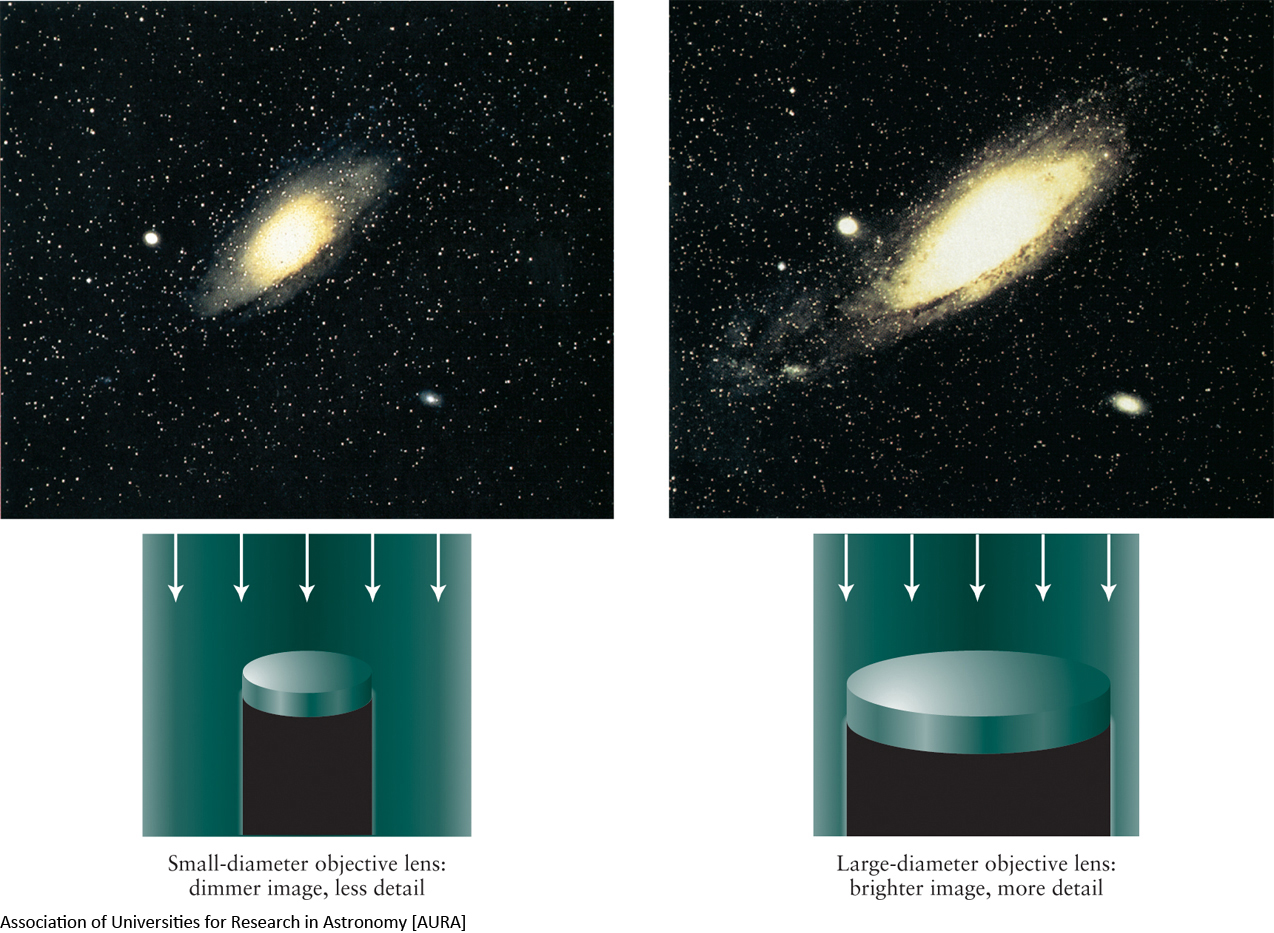
The most common belief about telescopes is that astronomers use telescopes to magnify stars so they can be studied. As it turns out, almost all telescopes show stars to be tiny pinpoints of light—regardless of the amount of magnification used. This is because stars are so very, very far away that magnification is not very helpful. On the other hand, telescopes are useful because they can capture light from very distant and dim objects and can collect and focus starlight from otherwise very dim stars into a central place to be studied. To aid in this effort of trying to make dim objects appear bright enough to be carefully studied, astronomers’ telescopes are constructed to have as much light-gathering ability as possible.
The most important dimension of a telescope is its diameter. Compared with a small-diameter telescope, a large-diameter telescope captures more light, produces brighter images, and allows astronomers to detect fainter objects. It is for this same reason that the iris of your eye opens wider when you go into a darkened room, to allow you to better see dimly lit objects.
The light-gathering power of a telescope is directly related to the size of its objective lens, the gathering area. In other words, the wider across your telescope’s objective lens is, the more light it can gather. Mathematically, the area of a telescope’s objective lens is directly related to the square of the telescope’s diameter (Figure 2-18). Thus, if you double the diameter of the telescope, the light-gathering power increases by a factor of 22 = 2 × 2 = Because light-gathering power is so important for seeing faint objects, the telescope’s diameter is almost always given in describing a telescope.
51
For example, the Lick Observatory telescope on Mount Hamilton in California is 90 cm in diameter. By comparison, Galileo’s telescope of 1610 was a much smaller 3 cm across. The Lick telescope is 30 times larger in diameter, and so has 30 × 30 = 900 times the light-gathering power of Galileo’s instrument.
Question
ConceptCheck 2-12: If someone says they are using an 8-inch telescope, which dimension of the telescope’s size are they most likely referring to?
Refracting Telescopes Use a Lens to Concentrate Incoming Light at a Focal Point
Which strategies can makers of telescopes use to gather and concentrate light to a central point? One is to use glass lenses, similar to those found in a common magnifying glass. In fact, the first telescopes recorded in history, those invented in the Netherlands in the early seventeenth century and the ones Galileo used for his groundbreaking astronomical observations, used lenses to make distant objects appear brighter and, in the case of the planets, somewhat larger.
The principle job of a telescope is to gather together light from a distant, dim object so it can be studied carefully, rather than just magnify it.
Lenses can be large or small, thick or thin, clear or coated, glass or plastic. Regardless of their exact specifications, lenses are characterized by how much they bend light. When a beam of light rays passes through a lens, all of the light converges to a single point. The distance from the lens to this special point is called the focal length of the lens. In order to view the image visually, a second lens to magnify the image is added. Such an arrangement of two lenses is called a refracting telescope (Figure 2-19). The large-diameter, long-focal-length lens at the front of the telescope, called the objective lens, forms the image; the smaller, shorter-focal-length lens at the rear of the telescope, called the eyepiece lens, magnifies the image for the observer.

52
Question
ConceptCheck 2-13: If a thick lens is able to bend light more than a thin lens, which lens has a greater focal length?
Magnification The ability of the two lenses working in concert not only provides a brighter image, but also a slightly larger one. As an example, the Moon as viewed with the naked eye is much smaller across than when viewed with even a small telescope. When Galileo viewed the Moon through his telescope, the moon appeared large enough so that he could identify craters and mountain ranges. The magnifying power, or magnification, of a telescope is the ratio of how big an object is when seen through the telescope compared to its naked-eye size.
The magnification of a refracting telescope depends on the focal lengths of both of its lenses:
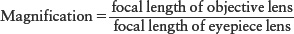
This formula shows that using a long-focal-length objective lens with a short-focal-length eyepiece gives a large magnification. Box 2-4 Tools of the Astronomer’s Trade: Magnification and Light-Gathering Power illustrates how this formula is used.
Question
ConceptCheck 2-14: How do the eyepieces with the largest focal length affect a telescope’s overall magnification?
Reflecting Telescopes Use a Mirror to Concentrate Incoming Light at a Focal Point
The second and more efficient approach of telescope makers to gather and focus light is to use curved mirrors rather than lenses. A telescope that uses a curved mirror to make an image of a distant object is called a reflecting telescope. Using terminology similar to that used for reflecting telescopes and illustrated in Figure 2-20, the mirror that forms the image is called the objective mirror, or primary mirror. In much the same way that a glass lens is able to concentrate light at a single point, a curved mirror also has a point at which light comes together at the focal length from the primary mirror. Telescope mirrors are commonly made from shaped glass with silver, aluminum, or a similar highly reflective substance applied to make them reflective.
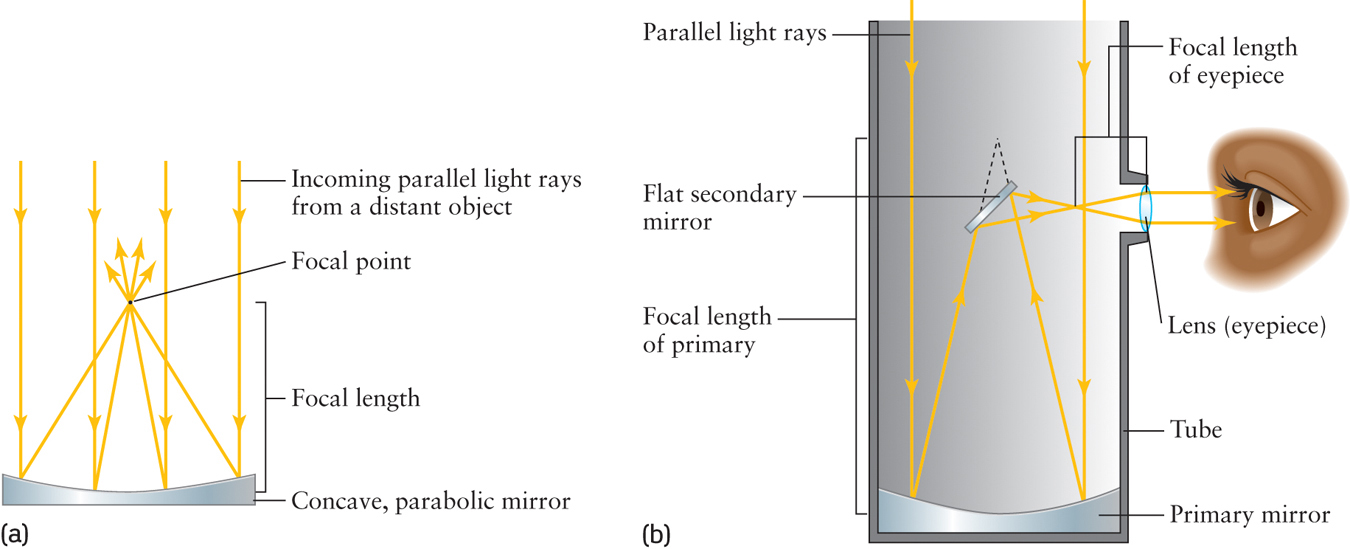
Because light reflects off the surface of the glass rather than passing through it, defects within the glass—which would have very negative consequences for the objective lens of a refracting telescope—have no effect on the optical quality of a reflecting telescope. Telescopes can be made much larger when made from mirrors than when made from glass. More importantly, these giant mirrors can be made out of materials that are significantly lighter and more durable than heavy glass, making them easier to point and less delicate to clean.
Although a reflecting telescope has many advantages over a refracting telescope, the arrangement shown in Figure 2-20 is not ideal. One problem is that the focal point is in front of the objective mirror. If you try to view the image formed at the focal point, your head will block part or all of the light from reaching the mirror. To get around this, the light is usually directed out of the telescope after bouncing off the primary mirror, often by the use of additional, or secondary, mirrors.
For astronomers, the most important thing is that reflecting telescopes can be constructed to be extremely large and have tremendous power to gather light from the dimmest of objects. As of 2013, there were 15 optical reflectors in operation with primary mirrors between 8 m (26.2 ft) and 11 m (36.1 ft) in diameter. These are very large indeed! Figure 2-21 shows the inner workings and seven enormous objective mirrors of the Giant Magellan Telescope, planned for completion in 2020 and being built in the Andes in Chile. These seven mirrors with diameters of 8.4 m (27.6 ft) add their light together and work as if they were one telescope with a total diameter of 22 m (72 ft) across. This telescope will have enough light-gathering power to capture light from some of the dimmest objects ever observed in the distant universe.

53
TOOLS OF THE ASTRONOMER’S TRADE
Magnification and Light-Gathering Power
The magnification of a telescope is equal to the focal length of the objective lens divided by the focal length of the eyepiece lens. Telescopic eyepieces are usually interchangeable, so the magnification of a telescope can be changed by using eyepieces of different focal lengths.
EXAMPLE: A small refracting telescope has an objective lens of focal length 120 cm. If the eyepiece has a focal length of 4.0 cm, what is the magnification of the telescope?
Situation: We are given the focal lengths of the telescope’s objective and eyepiece lenses. Our goal is to calculate the magnification provided by this combination of lenses.
Tools: We use the relationship that the magnification equals the focal length of the objective (120 cm) divided by the focal length of the eyepiece (4.0 cm).
Answer: Using this relationship,

Review: A magnification of 30× means that as viewed through this telescope, a large lunar crater that subtends an angle of 1 arcmin to the naked eye will appear to subtend an angle 30 times greater, or 30 arcmin (one-half of a degree). This makes the details of the crater much easier to see.
If a 2.0-cm-focal-length eyepiece is used instead, the magnification will be (120 cm)/(2.0 cm) = 60×. The shorter the focal length of the eyepiece, the greater the magnification.
The light-gathering power of a telescope depends on the diameter of the objective lens; it does not depend on the focal length. The light-gathering power is proportional to the square of the diameter. As an example, a fully dark adapted human eye has a pupil diameter of about 5 mm. By comparison, a small telescope whose objective lens is 5 cm in diameter has 10 times the diameter and 102 = 100 times the light-gathering power of the eye. (Recall that there are 10 mm in 1 cm.) Hence, this telescope allows you to see objects 100 times fainter than you can see without a telescope.
EXAMPLE: The same relationships apply to reflecting telescopes. Each of the two Keck telescopes on Mauna Kea in Hawaii (see Figure 2-28) uses a concave mirror 10 m in diameter to bring starlight to a focus. How many times greater is the light-gathering power of either Keck telescope than that of the human eye?
Situation: We are given the diameters of the pupil of the human eye (5 mm) and of the mirror of either Keck telescope (10 m). Our goal is to compare the light-gathering powers of these two optical instruments.
Tools: We use the relationship that light-gathering power is proportional to the square of the diameter of the area that gathers light. Hence, the ratio of the light-gathering powers is equal to the square of the ratio of the diameters.
Answer: We first calculate the ratio of the diameter of the Keck mirror to the diameter of the pupil. To do this, we must first express both diameters in the same units. Because there are 1000 mm in 1 m, the diameter of the Keck mirror can be expressed as
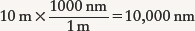
Thus, the light-gathering power of either of the Keck telescopes is greater than that of the human eye by a factor of
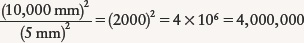
Review: Either Keck telescope can gather 4 million times as much light as a human eye. When it comes to light-gathering power, the bigger the telescope, the better!
Drawbacks of Refracting Telescopes When building extremely large telescopes with enormous light-gathering power, there are several negative aspects of reflecting telescopes that even the finest optician cannot overcome. First, because faint light must readily pass through the objective lens first, the glass from which the lens is made must be totally free of defects, such as the bubbles that frequently form when molten glass is poured into a mold. Such defect-free glass is extremely expensive. Second, glass is opaque to certain kinds of light. Ultraviolet light is absorbed almost completely, and even visible light is dimmed substantially as it passes through the thick slab of glass that makes up the objective lens. Third, it is impossible to produce a large lens that bends light of all wavelengths in equal amounts. Fourth, because glass lenses are extremely heavy, yet can be supported only around their edges, they can sag and distort under their own weight. This has dramatically negative effects on the image clarity.
Several other reflecting telescopes around the world have objective mirrors between 3 m and 6 m in diameter—which is still quite large—and dozens of smaller but still powerful telescopes have mirrors in the range of 1 m to 3 m. There are thousands of professional astronomers, each of whom has several ongoing research projects, and thus the demand for all of these telescopes is high. On any night of the year, nearly every research telescope in the world is being used to explore the universe.
54
Question
ConceptCheck 2-15: In large sizes, which type of telescope can be made lightest and most inexpensively?
Recent Advances in Technology Dramatically Improve Telescope Performance and Place Telescopes Above Earth’s Atmosphere
If telescopes can make dim objects appear brighter so they can be studied more carefully, telescopes can also make objects clearer. Imagine one night that you are watching the headlights of very distant cars and motorcycles slowly moving toward you. For the most distant of cars, it is difficult to distinguish the twin headlights on a car from the single headlight of a motorcycle. In fact, it is only when the vehicles get relatively close to you that you can determine which are double headlighted cars and which are single headlighted motorcycles. Just how close do these cars need to be for you to resolve the headlights as single or double? Your ability to see two glowing objects as distinct and separate light sources is called angular resolution, and it gauges how well fine details can be seen. Because of the blurring effects of Earth’s surrounding atmosphere, the resolution of a telescope can be limited when trying to observe two stars very close to one another or to see fine details on a planet’s surface.
When you are asked to read the letters on an eye chart, essentially what is being measured is the angular resolution of your eye. If you have 20/20 vision, the angular resolution of your eye is about 1 arcmin, or 60 arcsec. (You may want to review Box 1-1 Tools of the Astronomer’s Trade: Measuring Positions in the Sky.) Hence, with the naked eye it is impossible to distinguish two stars less than 1 arcmin apart or to see details on the Moon with an angular size smaller than this. All the planets have angular sizes (as seen from Earth) of less than 1 arcmin, which is why they appear as featureless points of light to the naked eye. One factor limiting angular resolution is the tendency of light waves to naturally spread out when they are confined to a small area like the lens or mirror of a telescope. This effect can cause star images to blur together. In astronomy, poor angular resolution causes star images to be fuzzy and blurred together.
Which characteristics are most important in determining a telescope’s angular resolving power? Diameter is almost everything in terms of importance. The specific wavelength of light also plays a role because shorter wavelengths of light are easier to resolve than longer wavelengths.
In practice, however, ordinary optical telescopes cannot achieve the highest levels of resolution due to the blurring effects of Earth’s atmosphere. In many cases the angular resolution of a telescope can be augmented by rapidly changing a mirror’s shape using a technique called adaptive optics. The goal of adaptive optics is to compensate for blurring atmospheric turbulence, which causes the image of a star to “dance” around erratically. Optical sensors monitor this dancing motion 10 to 100 times per second, and a powerful computer rapidly calculates the mirror shape needed to compensate. Fast-acting mechanical devices called actuators then deform the mirror accordingly. In some adaptive optics systems, the actuators deform a small secondary mirror rather than the large objective mirror.
55
One difficulty with adaptive optics is that a fairly bright star must be in or near the field of the telescope’s view to serve as a “target” for the sensors that track atmospheric turbulence. This is seldom the case, because the field of view of most telescopes is rather narrow. Astronomers get around this limitation by shining a laser beam toward a spot in the sky near the object to be observed (Figure 2-22). The laser beam causes atoms in the upper atmosphere to glow, making an artificial “star.” The light that comes down to Earth from this “star” travels through the same part of our atmosphere as the light from the object being observed, so its image in the telescope will “dance” around in the same erratic way as the image of a real star.

Figure 2-23 shows the dramatic improvement in angular resolution possible with adaptive optics. Images made with adaptive optics are nearly as sharp as if the telescope were in the vacuum of space, where there is no atmospheric distortion whatsoever and the only limit on angular resolution is diffraction. A number of large telescopes are now being used with adaptive optics systems.

Question
ConceptCheck 2-16: If astronomers are using an adaptive optics system on a night where the atmosphere is unusually turbulent, will the adaptive optics actuators be deforming the telescope’s mirror more rapidly or less rapidly than on a typical night?
Telescopes in Orbit Around Earth Detect and Resolve Light that Does Not Penetrate the Atmosphere
In addition to the distortion caused by Earth’s atmosphere, another challenge to astronomers is that Earth’s atmosphere blocks much of the light emitted by stars in ways that even the better telescopes under Earth’s atmosphere cannot fix. Figure 2-24 shows the transparency of Earth’s atmosphere to different wavelengths of light. The atmosphere is most transparent in two wavelength regions—visible light and radio waves. There are also several relatively transparent regions at infrared wavelengths between 1 m and 40 μm. Infrared light within these wavelength intervals can penetrate Earth’s atmosphere somewhat and can be detected with ground-based telescopes. This wavelength range is called the near-infrared, because it lies just beyond the red end of the visible light regime.
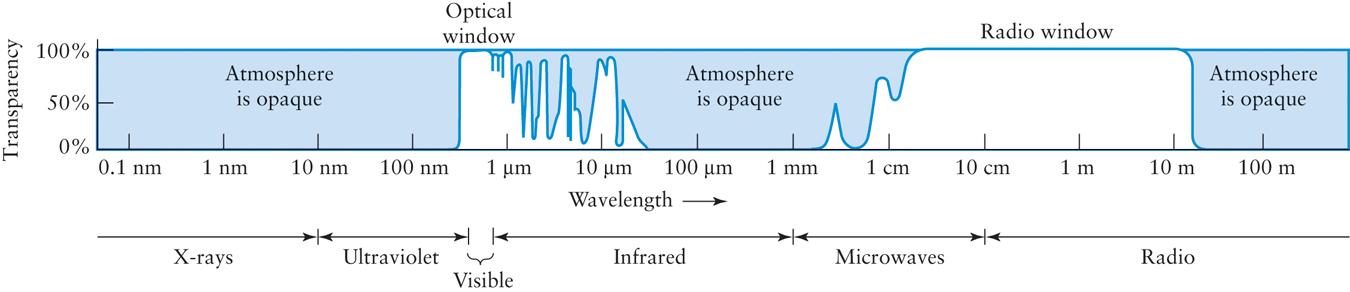
One factor over which astronomers have absolutely no control is the weather. Optical telescopes cannot see through clouds, so it is important to build observatories where the weather is usually good. Mountaintop observatories in particular benefit from most of the clouds forming at altitudes below the observatory, giving astronomers a better chance of having clear skies. Regardless of how high your mountaintop perch is, in many ways, the best location for a telescope is orbiting around Earth in outer space, where it is unaffected by weather, light pollution, or atmospheric turbulence.
56
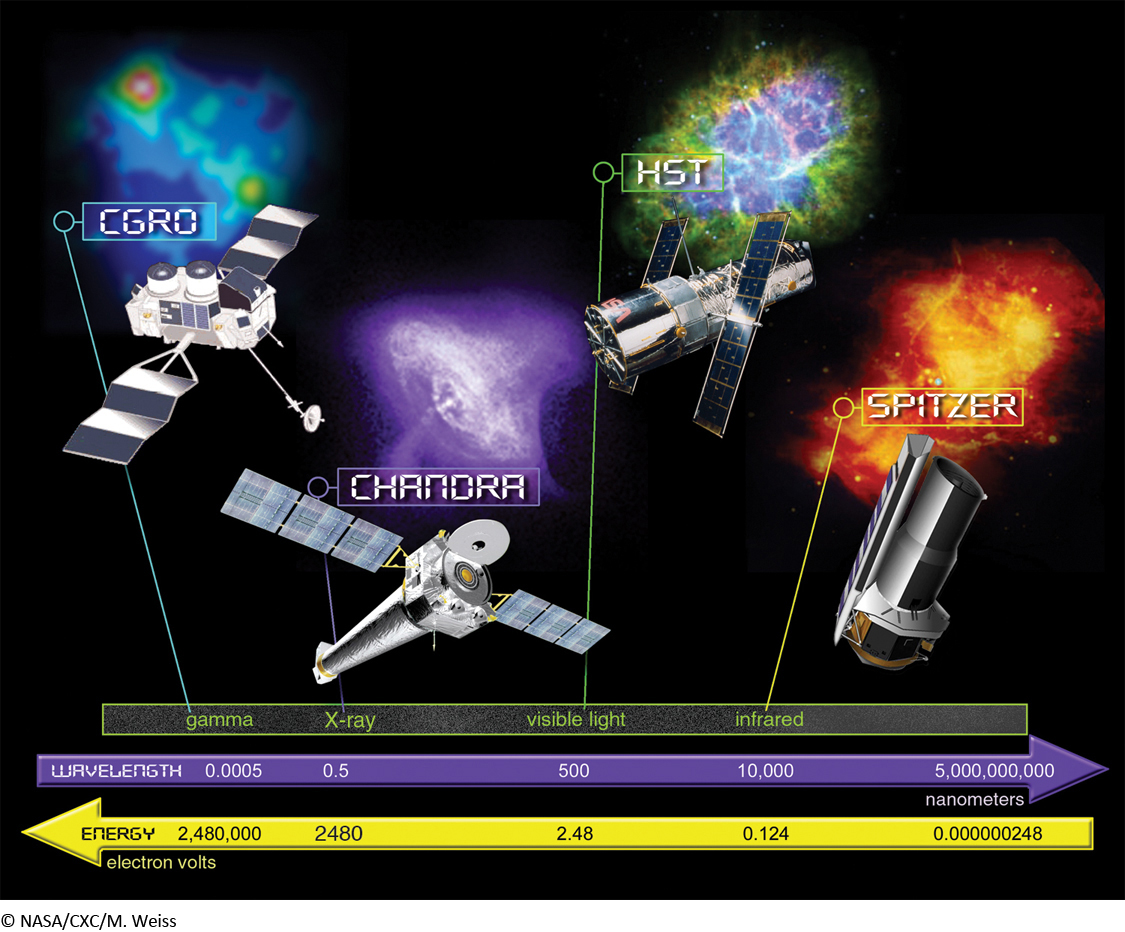
Figure 2-25 illustrates four telescopes of NASA’s Great Observatories program. Each mission is specially designed to look at a particular region of the electromagnetic spectrum. The Compton Gamma Ray Observatory (CGRO) was designed to capture the highly elusive, shortest wavelength gamma rays and discovered 3000 intense energy bursts from the formation of black holes and the merging of neutron stars (discussed in Chapter 12). The Chandra X-ray Observatory was launched because X-rays from outer space rarely penetrate Earth’s protective atmosphere. Chandra was the first telescope to make false-color images of high temperature gas near exotic neutron stars and black holes.
CAUTION
X-ray telescopes work on a very different principle from the X-ray devices used in medicine and dentistry. If you have your foot X-rayed to check for a broken bone, a piece of photographic film (or an electronic detector) sensitive to X-rays is placed under your foot and an X-ray beam is directed at your foot from above. The X-rays penetrate through soft tissue but not through bone, so the bones cast an “X-ray shadow” on the film. A fracture will show as a break in the shadow. X-ray telescopes, by contrast, do not send beams of X-rays toward astronomical objects in an attempt to see inside them. Rather, these telescopes detect X-rays that the objects emit on their own.
The Hubble Space Telescope (HST) made observations in the ultraviolet, visible, and infrared light regimes and was able to precisely measure the rate at which our universe is expanding (described in Chapter 15) and obtain images of the most distant galaxies in the universe as well as unprecedented views of our solar system’s planets. At the longer wavelength end, the Space Infrared Telescope Facility launched the Spitzer Space Telescope, which is able to peer inside interstellar dust clouds to observe the youngest stars just as they are forming. There are other space telescopes, but these four Great Observatories illustrate some of the wide range of what astronomers have been able to accomplish by observing from space.
The success of the Hubble Space Telescope has inspired plans for its larger successor, the James Webb Space Telescope (JWST). Planned for a 2016 launch, JWST will observe at visible and infrared wavelengths from 600 nm to 28 μm. With its 6.5-m objective mirror—2.5 times the diameter of the HST objective mirror, with 6 times the light-gathering power—JWST will study faint objects such as planetary systems forming around other stars and galaxies near the limit of the observable universe. Unlike HST, which is in a relatively low-altitude orbit around Earth, JWST will orbit the Sun some 1.5 million km beyond Earth. In this orbit the telescope’s view will not be blocked by Earth. Furthermore, by remaining far from the radiant heat of Earth, it will be easier to keep JWST at the very cold temperatures required by its infrared detectors.
57
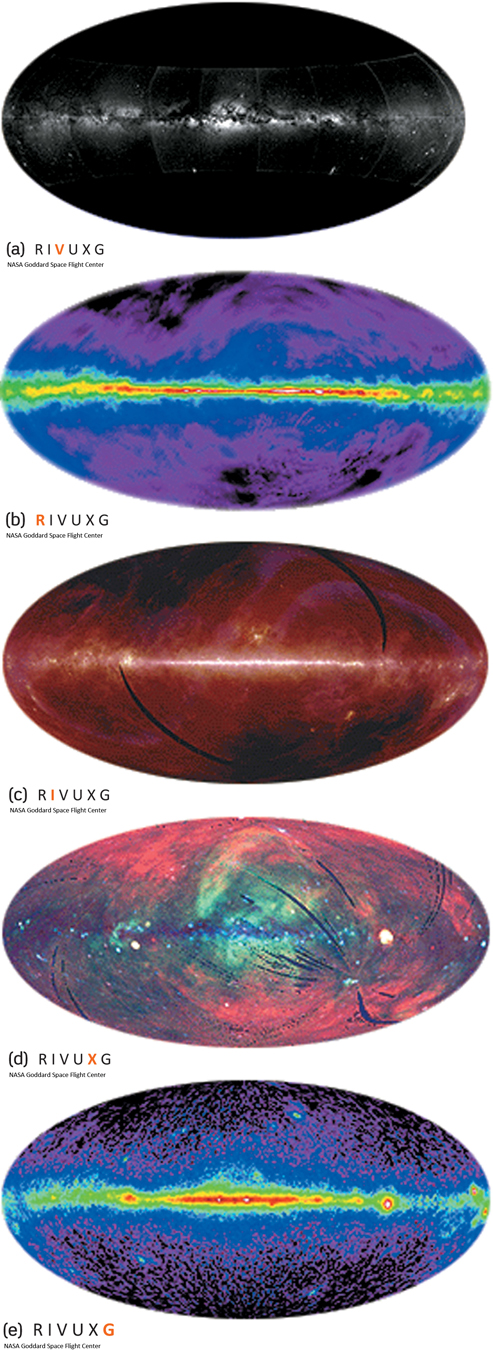
The advantages and benefits of Earth-orbiting observatories cannot be overemphasized. We are no longer limited to the narrow ranges of whatever wavelengths manage to leak through our shimmering, hazy atmosphere (Figure 2-26). For the first time, we are really seeing the universe.
Question
ConceptCheck 2-17: Look at Figure 2-26, which shows the transparency of Earth’s atmosphere. Would astronomers most prefer to have a new ground-based telescope constructed that is most sensitive in the X-ray region, the ultraviolet wavelength region, or the microwave region?
Question
ConceptCheck 2-18: What is the primary advantage of an orbiting space telescope, compared to a ground-based telescope?
Charge-Coupled Devices Record Very Fine Image Details
Until this point, we have been targeting our discussion on how telescopes capture light. The other half of the story is how the captured light is recorded for later study. For the past hundred years, astronomers primarily used photographic film or photographic plates. Unfortunately, photographic film is not a very efficient light detector. Only about 2% of the light striking photographic film is able to trigger the chemical reaction needed to produce an image. Thus, roughly 98% of the light falling onto photographic film is wasted.
The most sensitive light detector currently available to astronomers is the charge-coupled device (CCD). At the heart of a CCD is a semiconductor wafer divided into an array of small light-sensitive squares called picture elements or, more commonly, pixels. For example, each of the 40 CCDs shown in Figure 2-27a has more than 9.4 million pixels arranged in 2048 rows by 4608 columns. They have about 1000 times more pixels per square centimeter than a typical computer screen has, which means that a CCD of this type can record very fine image details. CCDs with smaller numbers of pixels are used in digital cameras, scanners, and fax machines.

58
When an image from a telescope is focused on the CCD, an electric charge builds up in each pixel in proportion to the number of photons falling on that pixel. When the exposure is finished, the amount of charge on each pixel is read into a computer, where the resulting image can be stored in digital form and either viewed on a monitor or printed out. Compared with photographic film, CCDs are some 35 times more sensitive to light (they commonly respond to 70% of the light falling on them, versus 2% for film), can record much finer details, and respond more uniformly to light of different colors. Figures 2-27b, c, and d show the dramatic difference between photographic and CCD images. The great sensitivity of CCDs also makes them useful for measuring the brightnesses of stars and other astronomical objects.
In the modern world of CCD astronomy, astronomers no longer need to spend the night in the unheated dome of a telescope on a windy mountaintop far from civilizations. Instead, they operate the telescope electronically from a separate control room, where the electronic CCD images can be viewed on a computer monitor. The control room need not even be adjacent to the telescope. Although the Keck I and II telescopes (Figure 2-28) are at an altitude of 13,600 ft (4145 m), astronomers can now make observations from a facility elsewhere on the island of Hawaii that is much closer to sea level. This saves the laborious drive up to Mauna Kea and eliminates the need for astronomers to acclimate to the high altitude.

59
Most of the images that you will see in this book were made with CCDs. Because of their extraordinary sensitivity and their ability to be used in conjunction with computers, CCDs have attained a role of central importance in astronomy. For scientists and engineers on the cutting edge of technology, the next advancements are all focused on making CCDs faster and yet with more pixels, but on smaller platforms. In a very short time, this technology will filter down quickly to make better cell phone cameras, higher-definition video cameras, and high quality Web cams at unbelievably low prices.
Question
ConceptCheck 2-19: Why can CCDs more efficiently observe faint stars than photographic film or photographic plates?
60