13.2 Tangent Planes
OBJECTIVES
When you finish this section, you should be able to:
- Find a tangent plane to a surface (p. 876)
- Find a normal line to a tangent plane (p. 876)
Earlier (Chapter 4), we saw the role of the tangent line in locating local maxima and local minima of a differentiable function \(y=f(x).\) For a surface, \(z=f(x,y)\), the tangent plane plays a similar role.
spanDEFINITIONspan Tangent Plane to a Surface
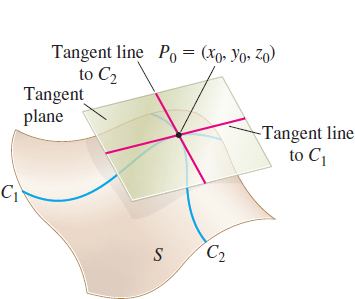
Let \(P_{0}=(x_{0},y_{0},z_{0})\) be a point on a surface \(S\), and let \(C\) be any smooth curve containing the point \(P_{0}\) and lying entirely on \(S\) . If the tangent lines to all such curves \(C\) at \(P_{0}\) lie in the same plane, then this plane is called the tangent plane to \(S\) at \(P_0\). See Figure 9.
NEED TO REVIEW?
A smooth curve is discussed in Section 9.2, pp. 647-648.
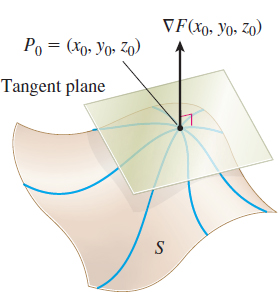
Now suppose the surface \(S\) is defined implicitly by the equation \( F(x,y,z)=0.\) Then \(S\) is equivalent to a level surface of the function \( w=F(x,y,z) .\) Let \(P_{0}=(x_{0},y_{0},z_{0})\) be a point on the surface \(S\). Suppose \(F\) is differentiable at \(P_{0}\) and \({\boldsymbol \nabla} F(x_{0},y_{0},z_{0})\neq \mathbf{0}.\) Then the gradient \({\boldsymbol \nabla} F(x_{0},y_{0},z_{0})\) is normal to the level surface that contains the point \(P_{0}.\) That is, for any smooth curve \(C\) on the surface \(S\) that contains the point \(P_{0}\), the tangent lines to \(C\) at \(P_{0}\) are orthogonal to the vector \({\boldsymbol \nabla}F(x_{0},y_{0},z_{0}).\) As a result, the tangent lines to \(C\) at the point \(P_{0}\) all lie in the same plane, and the surface \(S\) has a tangent plane at \(P_{0}\).
876
NEED TO REVIEW?
The equation of a plane is discussed in Section 10.6, pp. 737-738.
See Figure 10. Suppose \((x,y,z)\) is any point on the tangent plane to \(S\) at the point \(P_{0}=(x_{0},y_{0},z_{0})\). Since \({\boldsymbol \nabla }F(x_{0},y_{0},z_{0})\) is normal to the tangent plane at \( P_{0}\), an equation of the tangent plane is \[ {\boldsymbol \nabla }F(x_{0},y_{0},z_{0})\,{\bf\cdot}\, \lbrack (x-x_{0})\mathbf{i} +(y-y_{0})\mathbf{j}+(z-z_{0})\mathbf{k}]=0 \]
where \((x-x_{0})\mathbf{i}+(y-y_{0})\mathbf{j}+(z-z_{0})\mathbf{k}\) is a vector in the direction of the tangent line to a smooth curve \(C\) at the point \(P_{0}.\) Since \[ {\boldsymbol \nabla}F(x_{0},y_{0},z_{0})=F_{x}(x_{0},y_{0},z_{0})\mathbf{i} +F_{y}(x_{0},y_{0},z_{0})\mathbf{j}+F_{z}(x_{0},y_{0},z_{0})\mathbf{k} \]
an equation of the tangent plane is \[ F_{x}(x_{0},y_{0},z_{0})(x-x_{0})+F_{y}(x_{0},y_{0},z_{0})(y-y_{0})+F_{z}(x_{0},y_{0},z_{0})(z-z_{0})=0 \]
THEOREM Equation of a Tangent Plane
If \(F\) is differentiable at a point \(P_{0}=(x_{0},y_{0},z_{0})\) on the surface \(F(x,y,z)=0,\) and if \({\boldsymbol \nabla }F(x_{0},y_{0},z_{0})\neq \mathbf{0}\), then the surface has a tangent plane at \(P_{0}\). An equation of the tangent plane at \(P_{0}\) is \[ {\bbox[#FAF8ED]{\bbox[5px, border:1px solid black, #F9F7ED]{ F_{x}(x_{0},y_{0},z_{0})(x-x_{0})+F_y(x_{0},y_{0},z_{0})(y-y_{0})+F_{z}(x_{0},y_{0},z_{0})(z-z_{0})=0 }}} \]
1 Find a Tangent Plane to a Surface
Finding an Equation of a Tangent Plane to a Surface
Find an equation of the tangent plane to the hyperboloid of one sheet \( x^{2}+y^{2}-z^{2}=24\) at the point \((3,-4,1)\).
Solution The surface is given by the function \( F(x,y,z)=x^{2}+y^{2}-z^{2}-24=0.\) The partial derivatives of \(F\) are \[ F_{x}(x,y,z)=2x\qquad F_{y}(x,y,z)=2y\qquad F_{z}(x,y,z)=-2z \]
At the point \((3,-4,1)\), the partial derivatives are \[ F_{x}(3,-4,1)=6\qquad F_{y}(3,-4,1)=-8\qquad F_{z}(3,-4,1)=-2 \]
An equation of the tangent plane at \((3,-4,1)\) is \[ \begin{array}{rcl@{\quad}l} 6(x-3)-8(y+4)-2(z-1)& =& 0 & \\[4pt] 3x-4y-z& =&24 & \end{array} \]
Figure 11 shows the hyperboloid and part of the tangent plane at the point \((3,-4,1)\).
NEED TO REVIEW?
Lines in space are discussed in Section 10.6, pp. 733-736.
NOW WORK
Problems 3 and 11(a).
2 Find a Normal Line to a Tangent Plane
The line normal to the tangent plane to a surface \(F(x,y,z)=0\) at the point \(P_{0}=(x_{0},y_{0},z_{0})\) is called the normal line to the surface at \(P_{0}.\) Since the gradient \({\boldsymbol \nabla }F(x_{0},y_{0},z_{0})\) is normal to the tangent plane at \(P_{0}\), it follows that the normal line is in the direction of the gradient. The vector equation of the normal line is \[ {\bbox[#FAF8ED]{\bbox[5px, border:1px solid black, #F9F7ED]{ \mathbf{r}(t)=\mathbf{r}_{0}+t{\boldsymbol \nabla }F(x_{0},y_{0},z_{0}) }}} \]
where \(\mathbf{r}_{0}=x_{0}\mathbf{i}+y_{0}\mathbf{j}+z_{0}\mathbf{k}\) is the position vector of \(P_{0}\) and \(\mathbf{r}\) is the position vector of any point \(P\) on the normal line.
The corresponding parametric equations of the normal line are \[ {\bbox[#FAF8ED]{\bbox[5px, border:1px solid black, #F9F7ED]{ x=x_{0}+at\qquad y=y_{0}+bt\qquad z=z_{0}+ct }}}\]
877
where \(a=F_{x}(x_{0},y_{0},z_{0})\), \(b=F_{y}(x_{0},y_{0},z_{0})\), and \( c=F_{z}(x_{0},y_{0},z_{0})\). If \(abc\neq 0\), symmetric equations of the normal line are \[ {\bbox[#FAF8ED]{\bbox[5px, border:1px solid black, #F9F7ED]{ \dfrac{x-x_{0}}{a}=\dfrac{y-y_{0}}{b}=\dfrac{z-z_{0}}{c} }}} \]
Finding a Normal Line to a Tangent Plane
Find symmetric equations of the normal line to the hyperboloid of one sheet defined by the equation \(x^{2}+y^{2}-z^{2}=24\) at the point \((3,-4,1)\).
Solution The surface is given by \(F(x,y,z) =x^{2}+y^{2}-z^{2}-24=0.\) From Example 1, \({\boldsymbol \nabla } F( 3,-4,1) =6\mathbf{i}-8\mathbf{j}-2\mathbf{k}\). Since the normal line is in the direction of the gradient, symmetric equations of the normal line to the hyperboloid at \((3,-4,1)\) are \[ \frac{x-3}{6}=\frac{y+4}{-8}=\frac{z-1}{-2} \]
NOW WORK
Problem 11(b).
Surfaces Defined Explicitly by \(z=f( x,y)\)
To find an equation of the tangent plane to the surface \(z=f(x,y)\) at \( (x_{0},y_{0},z_{0})\), \(z_{0}=f(x_{0},y_{0}),\) we write the equation of the surface implicitly as \[ F(x,y,z)=z-f(x,y)=0 \]
Then \[ F_{x}=-f_{x}\qquad F_{y}=-f_{y}\qquad F_{z}=1 \]
An equation of the tangent plane to \(z=f(x,y)\) at \((x_{0},y_{0},z_{0})\) is \[ \begin{eqnarray*} &&F_{x}( x_{0},y_{0},z_{0}) (x-x_{0}) +F_{y}(x_{0},y_{0},z_{0}) ( y-y_{0}) +F_{z}(x_{0},y_{0},z_{0}) ( z-z_{0}) =0 \\[4pt] &&\hspace{42pt}-f_{x}(x_{0},y_{0})(x-x_{0})-f_{y}(x_{0},y_{0})(y-y_{0})+(z-z_{0}) =0 \end{eqnarray*} \] \[ {\bbox[#FAF8ED]{\bbox[5px, border:1px solid black, #F9F7ED]{ z-z_{0}=f_{x}(x_{0},y_{0})(x-x_{0})+f_{y}(x_{0},y_{0})(y-y_{0}) }}} \]
where \(z_{0}=f( x_{0},y_{0}).\) The parametric equations of the normal line to \(z=f(x,y) \) at the point \((x_{0},y_{0},z_{0}) \) are \[ {\bbox[#FAF8ED]{\bbox[5px, border:1px solid black, #F9F7ED]{ x=x(t)=x_{0}+tf_{x}(x_{0},y_{0})\qquad y=y(t)=y_{0}+tf_{y}(x_{0},y_{0})\qquad z=z(t)=z_{0}-t }}} \]