15.3 Fundamental Theorem of Line IntegralsPrinted Page 989
OBJECTIVES
When you finish this section, you should be able to:
In Example 6 of Section 15.2, we found a line integral along two different curves with common endpoints and obtained two different values. But there are situations where the curve connecting the two endpoints does not affect the value of the line integral ∫CF⋅dr; that is, the line integral is independent of the path. As it turns out, if the vector field F is conservative, then ∫CF⋅dr is independent of the path.
990
DEFINITION Conservative Vector Field; Potential Function
F is a conservative vector field if F is the gradient of some function f that has continuous first-order partial derivatives. That is, F is a conservative vector field if \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt] {{\bf{F}} = \nabla f}}
The function f is called a potential function for \mathbf{F}.
NEED TO REVIEW?
The gradient is discussed in Section 13.1, pp. 866-871.
1 Identifying a Conservative Vector Field and Its Potential FunctionPrinted Page 990
EXAMPLE 1Identifying a Conservative Vector Field and Its Potential Function
\mathbf{F}(x,y)=2xy\mathbf{i}+x^{2}\mathbf{j} is a conservative vector field, since \mathbf{F} is the gradient of the function f(x,y)=x^{2}y. That is, \nabla\! \ f(x,y)=f_{x}(x,y)\mathbf{i}+f_{y}(x,y)\mathbf{j}=2xy\mathbf{i}+x^{2}\mathbf{j}=\mathbf{F}(x,y)
The function f(x,y)=x^{2}y is the potential function for \mathbf{F}.
The next result provides a direct way to find the line integral \int_{c} \mathbf{F} \,\cdot\, d\mathbf{r} when \mathbf{F} is a conservative vector field.
THEOREM Fundamental Theorem of Line Integrals
Let \mathbf{F}=\mathbf{F}(x,y)=P(x,y)\mathbf{i}+Q(x,y)\mathbf{j} be a vector field, where the functions P(x,y) and Q(x,y) are continuous on some open region R containing the points (x_{0},y_{0}) and (x_{1},y_{1}). Let C be a piecewise-smooth curve beginning at the point (x_{0},y_{0}) and ending at the point (x_{1},y_{1}) that lies entirely in R. If \mathbf{F} is a conservative vector field on R, that is, if \mathbf{F} is the gradient of some function f so that \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt] { \mathbf{F}(x,y)=\nabla\! \ f(x,y)}}
throughout R, then \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt] { \int_{C}\mathbf{F}\,{\cdot}\, d\mathbf{r}=\int_{C}\nabla\! \ f\,{\cdot}\, d\mathbf{r}=\int_{(x_{0},y_{0})}^{(x_{1},y_{1})}\mathbf{F}\,{\cdot}\, d\mathbf{r}=\big[ f(x,y)\big]_{(x_{0},y_{0})}^{(x_{1},y_{1})}=f(x_{1},y_{1})-f(x_{0},y_{0}) }} \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt] { \int_{C}(P\,dx+Q\,dy)=\int_{(x_{0},y_{0})}^{(x_{1},y_{1})}(P \,dx+Q\,dy)=\big[ f(x,y)\big] _{(x_{0},y_{0})}^{(x_{1},y_{1})}=f(x_{1},y_{1})-f(x_{0},y_{0}) }}
Proof
This proof is for a smooth curve C. (The proof for a piecewise-smooth curve is obtained by considering one piece of the curve at a time.) Let x=x(t) and y=y(t), a\leq t\leq b, be parametric equations of a smooth curve C. The initial point and endpoint of C can then be written as (x_{0},y_{0})=(x(a),y(a))\qquad \hbox{and}\qquad (x_{1},y_{1})=(x(b),y(b))
Since \mathbf{F}=P(x,y)\mathbf{i}+Q(x,y)\mathbf{j} is a conservative vector field, then \mathbf{F}=\nabla\! \ f=\frac{\partial f}{\partial x}\mathbf{i}+\frac{\partial f}{\partial y}\mathbf{j} for some function f. Since \mathbf{F}=P(x,y) \mathbf{i}+Q(x,y) \mathbf{j}, it follows that P(x,y) =\frac{\partial f}{\partial x} and Q(x,y) =\frac{\partial f}{\partial y}. Then
\begin{eqnarray*} \int_{C}(P\,dx+Q\,dy)& =&\int_{C}\left( \frac{\partial f}{\partial x}\,dx+ \frac{\partial f}{\partial y}\,dy\right)=\int_{a}^{b}\left( \frac{\partial f }{\partial x}\frac{dx}{dt}+\frac{\partial f}{\partial y}\frac{dy}{dt}\right) \ \!dt\\ & =&\int_{a}^{b}\frac{d}{dt}[f(x(t),y(t))]\,dt\qquad {\color{#0066A7}{\hbox{Use the Chain Rule I: \(\frac{d}{dt} f (x ( t) ,y ( t))=\frac{\partial f}{\partial x}\frac{dx}{dt}+\frac{\partial f}{\partial y}\frac{dy}{dt}.\)}} }\\ & =&\big[ f(x(t),y(t))\big] _{t=a}^{t=b}\qquad\qquad\enspace {\color{#0066A7}{\hbox{Use the Fundamental Theorem of Calculus.}}}\\ & =&f(x(b),y(b))-f(x(a),y(a))=f(x_{1},y_{1})-f(x_{0},y_{0}) \end{eqnarray*}
991
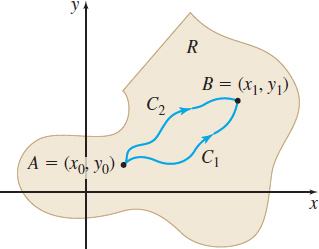
In the Fundamental Theorem of Line Integrals, the value of the line integral depends only on the endpoints (x_{0},y_{0}) and (x_{1},y_{1}) of the curve C. This means that the value of the line integral does not change if C is replaced by any other piecewise-smooth curve in R, provided the new curve connects (x_{0},y_{0}) to (x_{1},y_{1}). Figure 22 illustrates this for two curves C_{1} and C_{2} joining A=(x_{0},y_{0}) and B=(x_{1},y_{1}). As a result, line integrals \int_{C}\mathbf{F}\,{\cdot}\, d\mathbf{r} for which the conditions of the Fundamental Theorem of Line Integral are met are said to be independent of the path. In other words, for a conservative vector field \mathbf{F}, the line integral \int_{C}\mathbf{F}\,{\cdot}\, d\mathbf{r} has the same value no matter what path C is taken from A=(x_{0},y_{0}) to B=(x_{1},y_{1}). To summarize:
If \mathbf{F}={P\mathbf{i}} + {Q\mathbf{j}} = \nabla\! \ f, then:
- \int_{C} (P\,dx+Q\,dy)=f(x_{1},y_{1})-f(x_{0},y_{0}) for any piecewise-smooth curve C joining A and B.
- \int_{C_{1}} (P\,dx+Q\,dy)=\int_{C_{2}} (P\,dx+Q\,dy) for any piecewise-smooth curves C_{1} and C_{2} joining A and B.
2 Use the Fundamental Theorem of Line IntegralsPrinted Page 991
EXAMPLE 2Using the Fundamental Theorem of Line Integrals
\mathbf{F}=\mathbf{F}(x,y)=(2xy+24x)\mathbf{i}+(x^{2}+16)\mathbf{j} is a conservative vector field, since \mathbf{F} is the gradient of f(x,y)=x^{2}y+12x^{2}+16y. Use this fact to find \int_{C}\left[ (2xy+24x)\,dx+(x^{2}+16)\,dy\right]
where C is any piecewise-smooth curve joining the points (1,1) and (2,4).
Solution We use two methods to find \int_{C}[(2xy+24x)\,dx+(x^{2}+16)\,dy].
Method I uses the potential function f(x,y)=x^{2}y+12x^{2}+16y whose gradient is \nabla\! \ f=(2xy+24x)\mathbf{i}+(x^{2}+16)\mathbf{j}=\mathbf{F}(x,y)
and the Fundamental Theorem of Line Integrals. \begin{eqnarray*} \hspace{-250pt}\int_{C}[(2xy+24x)\,dx+(x^{2}+16)\,dy]=\big[ f(x,y)\big]_{(1,1)}^{(2,4)}=f(2,4)-f(1,1)\\[4pt] \hspace{0pt}= [ ( 2^{2}) ( 4) +12(2^{2}) +16( 4) ] -[ ( 1^{2}) (1) +12( 1^{2}) +16( 1) ] =99 \end{eqnarray*}
Method II uses the fact that the given line integral is independent of the path, so it can be integrated along any piecewise-smooth curve joining (1,1) and (2,4). We choose the path shown in Figure 23 since it makes the integration easy. So, along C_{1}, dy=0,
and along C_{2}, dx=0. Then \begin{eqnarray*} \hspace{-1.0pc}\int_{C}[(2xy+24x)\,dx+(x^{2}+16)\,dy]&=&\int_{C_{1}}[(2xy+24x)\,dx+(x^{2}+16)\,dy]\\[4pt] &&+\int_{C_{2}}[(2xy+24x)\,dx+(x^{2}+16)\,dy] \notag \\[4pt] &=& \int_{1}^{2}(2x+24x)\,dx+\int_{1}^{4}(4+16)\,dy=39+60=99 \end{eqnarray*}
992
Method I is easier to use than Method II, but this is because the potential function f of \mathbf{F} is given. If the potential function f had not been given, then we would have had to find it before using Method I. We discuss how to do this shortly.
NOW WORK
So, to find the line integral \int_{C}\mathbf{F}\,{\cdot}\, d\mathbf{r} =\int_{C}(P\,dx+Q\,dy), where \mathbf{F}=P\mathbf{i}+Q\mathbf{j} is a conservative vector field, either of the methods outlined in Example 2 can be used.
Finding \int_{C}\mathbf{F}\,{\cdot}\, d \mathbf{r}=\int_{C}(P\,dx+Q\,dy) for a Conservative Vector Field
Method I: Use the Fundamental Theorem of Line Integrals directly. That is, if \mathbf{F}=\nabla\! \ f, \int_{C}\mathbf{F}\,{\cdot}\, d\mathbf{r}=\int_{C}(P\,dx+Q\,dy)=f(x_{1},y_{1})-f(x_{0},y_{0})
Method II: Use the fact that \int_{C}(P\,dx+Q\,dy) is independent of the path and select some suitable path joining the endpoints of C that makes finding the line integral easy.
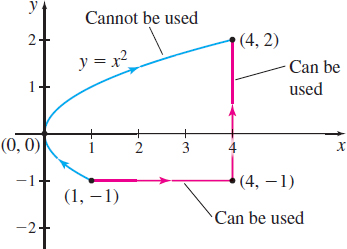
Care must be taken when using Method II. For example, suppose we are asked to find \int_{C}\frac{-y\,dx+x\,dy}{x^{2}}
along the curve C joining the points (1,-1) and (4,2). \bigg[\mathbf{F}=\mathbf{F}(x,y)=\frac{-y\mathbf{i}+x\mathbf{j}}{x^{2}} is a conservative vector field since \mathbf{F} is the gradient of the function \left.f(x,y)=\frac{y}{x}.\right] To use Method II to find the line integral, we cannot choose a path (such as x=y^{2}) that intersects the y-axis, because P=-\frac{y}{x^{2}} and Q=\frac{1}{x} are not defined at x=0. But any path that lies entirely in the first and fourth quadrants can be used. See Figure 24.
A special case of the Fundamental Theorem of Line Integrals occurs when C is a closed curve, that is, when the initial point (x_{0},y_{0}) equals the terminal point (x_{1},y_{1}). Then f(x_{1},y_{1})=f(x_{0},y_{0}) and the value of the line integral is \int_{C}(P\,dx+Q\,dy) =f(x_{1},y_{1}) -f(x_{0},y_{0}) =0 .
COROLLARY Value of a Line Integral over a Closed Curve
Suppose \mathbf{F} is a conservative vector field on some open region R, and C is a closed, piecewise-smooth curve that lies entirely in R. Then \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt] { \int_{C}\mathbf{F}\,{\cdot}\, d\mathbf{r}=\int_{C}(P\,dx+Q\,dy)=0 }}
993
EXAMPLE 3Finding a Line Integral over a Closed Curve
\mathbf{F}=\mathbf{F}(x,y)=\frac{-y\mathbf{i}+x\mathbf{j}}{x^{2}+y^{2}} is the gradient of f(x,y) =\tan ^{-1}\frac{y}{x}, x\neq 0, since \begin{equation*} \nabla\! \ f=\frac{\partial }{\partial x}\tan ^{-1}\frac{y}{x}\mathbf{i}+\frac{\partial }{\partial y}\tan ^{-1}\frac{y}{x}\mathbf{j}=\frac{ \frac{-y}{x^{2}}}{1+\frac{y^{2}}{x^2}}\mathbf{i}+\frac{\frac{1}{x}}{1+\frac{y^{2}}{x^2}}\mathbf{j}=\frac{-y\mathbf{i}+x\mathbf{j}}{x^{2}+y^{2}} \end{equation*}
So, \mathbf{F} is a conservative vector field on any region R that contains no points on the y-axis (x=0). Then by the corollary \begin{equation*} \int_{C}\mathbf{F}\,{\cdot}\, d\mathbf{r}=0 \end{equation*}
along any closed, piecewise-smooth curve C that does not cross or touch the y-axis.
NOW WORK
The Converse of the Fundamental Theorem of Line Integrals
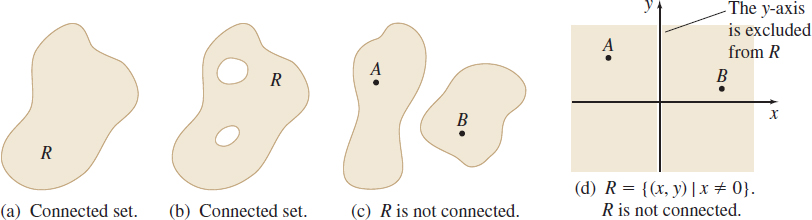
An open region R is connected if any two points in R can be joined by a piecewise-smooth curve C that lies entirely in R. Figure 25(a) and 25(b) illustrate the idea of a connected region. In these two figures, any two points of R can be joined by a piecewise-smooth curve that lies entirely in R, so R is connected. In Figure 25(c) and 25(d), R is not connected, since the points A and B cannot be joined by a curve that lies entirely in R.
From the Fundamental Theorem of Line Integrals, if \mathbf{F} is a conservative vector field on an open region R, then \int_{C}\mathbf{F} \,{\cdot}\, d\mathbf{r} is independent of the path taken in R. If R is connected, then the converse of the Fundamental Theorem of Line Integrals is also true.
NOTE
The converse of the conditional statement “If p, then q” is “If q, then p.”
THEOREM The Converse of the Fundamental Theorem of Line Integrals
Let \mathbf{F}=\mathbf{F}(x,y)=P(x,y)\mathbf{i}+Q(x,y)\mathbf{j} be a vector field, where the functions P(x,y) and Q(x,y) are continuous on an open, connected region R containing the point (x_{0},y_{0}). If the line integral \int_{C}\mathbf{F}\,{\cdot}\, d\mathbf{r}= \int_{C}(P\,dx+Q\,dy) for every piecewise-smooth curve C in R, is independent of the path, then the line integral \int_{C}\mathbf{F}\,\cdot\, d\mathbf{r} defines a function f(x,y) such that \nabla f=\mathbf{F}. In other words, \mathbf{F} is a conservative vector field on R.
Proof
Suppose \int_{C}(P\,dx+Q\,dy) has the same value for every piecewise-smooth curve C in R that joins (x_{0},y_{0}) to (x,y). That is, suppose \int_{C}(P\,dx+Q\,dy) is independent of the path. If C is any piecewise-smooth curve in R joining a fixed point (x_{0},y_{0}) to an arbitrary point (x,y), the line integral \int_{C}(P\,dx+Q\,dy) defines a function f that depends only on (x,y) and not on C. And, we can define \begin{equation*} f(x,y)=\int_{(x_{0},y_{0})}^{(x,y)}(P\,dx+Q\,dy) \end{equation*}
994
Since any piecewise-smooth curve C that lies entirely in R is allowed, we choose two paths, one in which a horizontal line segment is used, and another in which a vertical line segment is used. As Figure 26 illustrates:
C_{1}: Consists of a piecewise-smooth curve joining (x_{0},y_{0}) to ( x_{1},y) plus a horizontal line segment joining ( x_{1},y) to (x,y).
C_{2}: Consists of a piecewise-smooth curve joining (x_{0},y_{0}) to ( x,y_{1}) plus a vertical line segment joining ( x,y_{1}) to (x,y).
For path C_{1}, f(x,y)=\int_{(x_{0},y_{0})}^{(x,y)}(P\,dx+Q\,dy)=\int_{(x_{0},y_{0})}^{(x_{1},y)}(P\,dx+Q\,dy)+\int_{(x_{1},y)}^{(x,y)}(P \,dx+Q\,dy)
The first integral on the right is a function of y alone, since x_{0} and x_{1} are constants. So, its partial derivative with respect to x equals 0. That is, \frac{\partial }{\partial x}\int_{(x_{0},y_{0})}^{(x_{1},y)}(P\,dx+Q\,dy)=0
In the second integral on the right, the value of y is the same in both the lower and upper limits of integration, so it follows that dy=0. That is, \frac{\partial }{\partial x}\int_{(x_{1},y)}^{(x,y)}(P\,dx+Q\,dy)=\frac{\partial }{\partial x}\int_{x_{1}}^{x}\left[ P\,dx+0\right] =P(x,y)
Combining these two results, we find \begin{eqnarray*} \frac{\partial }{\partial x} \ f(x,y) &=&\frac{\partial }{\partial x} \int_{(x_{0},y_{0})}^{(x_{1},y)}(P\,dx+Q\,dy)+\frac{\partial }{\partial x} \int_{(x_{1},y)}^{(x,y)}(P\,dx+Q\,dy) = P(x,y) \end{eqnarray*}
For path C_{2}, f(x,y)=\int_{(x_{0},y_{0})}^{(x,y_{1})}(P\,dx+Q\,dy)+\int_{(x,y_{1})}^{(x,y)}(P\,dx+Q\,dy)
The first integral on the right is a function of x alone, since y_{0} and y_{1} are constants. So, the partial derivative with respect to y equals 0. That is, \begin{equation*} \frac{\partial }{\partial y}\int_{(x_{0},y_{0})}^{(x,y_{1})}(P\,dx+Q\,dy)=0 \end{equation*}
In the second integral on the right, the value of x is the same in both the lower and upper limits of integration, so it follows that dx=0. That is, \frac{\partial }{\partial y}\int_{(x,y_{1})}^{(x,y)}(P\,dx+Q\,dy)=\frac{ \partial }{\partial y}\int_{y_{1}}^{y}\left[ 0+Q(x,y)\,dy\right] =Q(x,y)
Combining these two results, we find \begin{eqnarray*} \frac{\partial }{\partial y} \ f(x,y) &=&\frac{\partial }{\partial y} \int_{(x_{0},y_{0})}^{(x,y_1)}(P\,dx+Q\,dy)+\frac{\partial }{\partial y} \int_{(x,y_{1})}^{(x,y)}(P\,dx+Q\,dy) = Q(x,y) \end{eqnarray*}
995
Finally, since \frac{\partial }{\partial x} \ f(x,y)=P(x,y) and \frac{\partial }{\partial y} \ f(x,y)=Q(x,y), we have \begin{equation*} \nabla\! \ f=\frac{\partial f}{\partial x}\mathbf{i}+\frac{\partial f}{\partial y}\mathbf{j}=P(x,y)\mathbf{i}+Q(x,y)\mathbf{j}=\mathbf{F} \end{equation*}
That is, the vector field \mathbf{F} is conservative.
3 Reconstruct a Function from Its Gradient: finding the Potential Function for a Conservative Vector FieldPrinted Page 995
Suppose \mathbf{F}=\mathbf{F}(x,y) is a conservative vector field. Then there is a potential function f so that \nabla \! \ f=\mathbf{F}. The proof of the converse of the Fundamental Theorem of Line Integrals provides a way of finding the potential function f when its gradient \nabla \! \ f=\mathbf{F} is known. This is called reconstructing a function from its gradient.
EXAMPLE 4Finding a Potential Function for a Conservative Vector Field
If it is known that \begin{equation*} \mathbf{F}=\mathbf{F}(x,y)=(6xy+y^{3})\mathbf{i}+(3x^{2}+3xy^{2})\mathbf{j} \end{equation*}
is a conservative vector field, find a potential function f for \mathbf{F}.
Solution We seek a function f(x,y) for which \begin{equation*} \nabla\! \ f=\mathbf{F}=(6xy+y^{3})\mathbf{i}+(3x^{2}+3xy^{2})\mathbf{j} \end{equation*}
Let P(x,y)=6xy+y^{3}\qquad \hbox{and}\qquad Q(x,y)=3x^{2}+3xy^{2}
Since \nabla\! \ f=\dfrac{\partial f}{\partial x}\mathbf{i}+\dfrac{\partial f}{ \partial y}\mathbf{j}=P(x,y)\mathbf{i}+Q(x,y)\mathbf{j}
we have \begin{eqnarray*} \dfrac{\partial f}{\partial x}=6xy+y^{3}\qquad \hbox{and}\qquad \dfrac{\partial f}{\partial y}=3x^{2}+3xy^{2}\tag{1} \end{eqnarray*}
Now integrate the left equation partially with respect to x. f(x,y) =\int ( 6xy+y^{3})\, dx=3x^{2}y+xy^{3}+h(y)
where the “constant of integration,” h(y), is a function of y.
Next differentiate f with respect to y: \begin{equation*} \dfrac{\partial f}{\partial y}=3x^{2}+3xy^{2}+h' (y) \end{equation*}
From (1), we have \begin{equation*} \dfrac{\partial f}{\partial y}=3x^{2}+3xy^{2} \end{equation*}
So, h' (y)=0 or h(y) =K, where K is a constant. A potential function f for \mathbf{F} is f(x,y)=3x^{2}y+xy^{3}+K
NOW WORK
You can verify that f is a potential function for \mathbf{F} by finding the gradient of f: \nabla\! \ f=\dfrac{\partial f}{\partial x}\mathbf{i}+\dfrac{\partial f}{\partial y}\mathbf{j}=(6xy+y^{3})\mathbf{i}+(3x^{2}+3xy^{2})\mathbf{j}=\mathbf{F}(x,y)
996
If we had chosen to integrate \dfrac{\partial f}{\partial y}=3x^{2}+3xy^{2} partially with respect to y, we would have obtained \begin{equation*} f(x,y)=3x^{2}y+xy^{3}+k(x) \end{equation*}
where the “ constant of integration,” k(x), is a function of x. Then \begin{equation*} \dfrac{\partial f}{\partial x}=6xy+y^{3}=6xy+y^{3}+k' (x) \end{equation*}
So, k' (x)=0 or k(x)=K, a constant, and \begin{equation*} f(x,y)=3x^{2}y+xy^{3}+K \end{equation*}
as before.
4 Determine Whether a Vector Field Is ConservativePrinted Page 996
As the solution to Example 4 illustrates, if \mathbf{F} is known to be a conservative vector field, then we can find its potential function f. But how do we determine if \mathbf{F} is a conservative vector field? Before giving the theorem, we need some definitions.
DEFINITION Closed Curve; Simple Curve
Let \mathbf{r}=\mathbf{r}(t), a\leq t\leq b, trace out a piecewise-smooth curve C.
- C is closed if \mathbf{r}(a)=\mathbf{r}(b).
- C is simple if it does not intersect itself for a<t<b.
IN WORDS
A curve C is closed if its initial point and its terminal point coincide.
See Figure 27.
DEFINITION Simply Connected
Let R denote a set of points in the plane. Then R is called simply connected if its boundary consists of a single, simple closed curve, and the interior of any simple closed curve C in R contains only points of R.
Intuitively, a set R is not simply connected if it has “holes” or if it consists of two or more separate pieces.
Figure 28(a) shows a region R that has a “hole.” Its boundary consists of two simple closed curves C_{1} and C_{2}. The curve C_{3} is a simple closed curve contained completely in the region, but the interior of C_{3} contains points that are not in the region R, so the region R is not simply connected.
Figure 28(b) shows a region R whose boundary consists of one simple closed curve C. Since the boundary C of R and the interior of any simple closed curve C in R contains only points in R, the region is simply connected.
Figure 28(c) shows a region R whose boundary consists of two simple closed curves C_{1} and C_{2}, that separate R into two pieces. So, R is not a simply connected region.
997
Now we are ready for the test to determine whether or not a vector field \mathbf{F} is conservative.
THEOREM Conservative Vector Field Test
Let \mathbf{F}=\mathbf{F}(x,y)=P(x,y)\mathbf{i}+Q(x,y)\mathbf{j} be a vector field, where the functions P and Q are continuous on some simply connected, open region R. Suppose \dfrac{\partial P}{\partial y} and \dfrac{\partial Q}{\partial x} are also continuous on R. Then \mathbf{F}(x,y)=P(x,y)\mathbf{i}+Q(x,y)\mathbf{j} is a conservative vector field on R if and only if \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt] { \dfrac{\partial P}{\partial y}=\dfrac{\partial Q}{ \partial x} }}
throughout R.
We only prove that if \mathbf{F} is a conservative vector field, then \dfrac{\partial P}{\partial y}=\dfrac{\partial Q}{\partial x}. The proof of the converse is generally found in advanced calculus texts. However, the proof of the converse for a special case is given in Section 15.5. See p. 1013.
Proof
Suppose that \mathbf{F}=\mathbf{F}(x,y)=P(x,y)\mathbf{i}+Q(x,y)\mathbf{j} is a conservative vector field. Then \mathbf{F} is the gradient of some function f. That is, \nabla\! \ f=\dfrac{\partial f}{\partial x}\mathbf{i}+\dfrac{\partial f}{ \partial y}\mathbf{j}=P(x,y)\mathbf{i}+Q(x,y)\mathbf{j}
Then \dfrac{\partial f}{\partial x}=P(x,y)\qquad \hbox{and}\qquad \dfrac{\partial f}{\partial y}=Q(x,y)
so that \dfrac{\partial ^{2}f}{\partial y\partial x}=\dfrac{\partial P}{\partial y} \qquad \hbox{and}\qquad \dfrac{\partial ^{2}f}{\partial x\partial y}=\dfrac{\partial Q}{ \partial x}
Since it is assumed that \dfrac{\partial P}{\partial y} and \dfrac{\partial Q}{\partial x} are continuous in R, we can use the Equality of Mixed Partials Theorem (page 835), which states that if the first-order partial derivatives and the second-order mixed partial derivatives exist at each point in some disk centered at (x_{0},y_{0}) and if the mixed partial derivatives are continuous at (x_{0},y_{0}), then f_{xy}(x_{0},y_{0})=f_{yx}(x_{0},y_{0}). As a result, \dfrac{\partial P}{\partial y}=\dfrac{\partial Q}{\partial x}
998
EXAMPLE 5Determining Whether \mathbf{F} Is a Conservative Vector Field
(a) \mathbf{F}=2xy\mathbf{i}+(x^{2}+1)\mathbf{j} is a conservative vector field on the entire xy-plane since \begin{equation*} \dfrac{\partial P}{\partial y}=\dfrac{\partial }{\partial y}(2xy)=2x\qquad \hbox{and}\qquad \dfrac{\partial Q}{\partial x}=\dfrac{\partial }{\partial x}(x^{2}+1)=2x \end{equation*}
are equal for any choice of (x,y).
(b) The vector field \mathbf{F}=\dfrac{x}{y^{2}}\mathbf{i}-\dfrac{x^{2}}{y^{3}}\mathbf{j} is conservative on any connected region not containing points on the x-axis (y=0) since \begin{equation*} \dfrac{\partial P}{\partial y}=\dfrac{\partial }{\partial y}\dfrac{x}{y^{2}} =-\dfrac{2x}{y^{3}} \qquad \hbox{and}\qquad \dfrac{\partial Q}{\partial x}=\dfrac{\partial }{\partial x}\left( -\dfrac{x^{2}}{y^{3}}\right) =-\dfrac{2x}{y^{3}} \end{equation*}
are equal, provided y\neq 0. Because \mathbf{F}=\dfrac{x}{y^{2}}\mathbf{i}-\dfrac{x^{2}}{y^{3}}\mathbf{j} is conservative for y\neq 0, the line integral \int_{C}\mathbf{F}\,{\cdot}\, d\mathbf{r}=\int_{C}\left[ \dfrac{x}{y^{2}}dx-\dfrac{x^{2}}{y^{3}}dy\right] is independent of the path in any simply connected region not containing points on the x-axis.
NOW WORK
EXAMPLE 6Finding a Potential Function for a Conservative Vector Field
- (a) Show that the line integral \int_{C}\mathbf{F}\,{\cdot}\, d\mathbf{r}=\int_{C}[(2xy+24x)\,dx+(x^{2}+16)\,dy] is independent of the path.
- (b) Find a function f for which \nabla \! \ f=(2xy+24x) \mathbf{i}+(x^{2}+16)\mathbf{j}.
- (c) Find \int_{C}[(2xy+24x)\,dx+(x^{2}+16)\,dy], where C is any piecewise-smooth curve joining (0,1) to (1,2).
Solution (a) Let P(x,y)=2xy+24x and Q(x,y)=x^{2}+16. Then \dfrac{\partial P}{\partial y}=2x and \dfrac{\partial Q}{\partial x}=2x. Since P, Q, \dfrac{\partial P}{\partial y}, and \dfrac{\partial Q }{\partial x} are continuous everywhere in the xy-plane and since \dfrac{ \partial P}{\partial y}=\dfrac{\partial Q}{\partial x}, then \mathbf{F}=\mathbf{F}(x,y)=(2xy+24x)\mathbf{i}+(x^{2}+16)\mathbf{j} is a conservative vector field. By the Fundamental Theorem of Line Integrals, \int_{C}\mathbf{F}\,{\cdot}\, d\mathbf{r} is independent of the path.
(b)Since \mathbf{F}=\mathbf{F}(x,y)=(2xy+24x)\mathbf{i}+(x^{2}+16)\mathbf{j} is a conservative vector field, there is a potential function f for \mathbf{F} for which \nabla\! \ f=\mathbf{F}=(2xy+24x)\mathbf{i}+(x^{2}+16)\mathbf{j}
Since \nabla\! \ f=\dfrac{\partial f}{\partial x}\mathbf{i}+\dfrac{\partial f}{\partial y}\mathbf{j}, then \begin{equation*} \dfrac{\partial f}{\partial x}=2xy+24x\qquad \hbox{and}\qquad \dfrac{\partial f}{\partial y}=x^{2}+16 \end{equation*}
We integrate the first of these partial derivatives partially with respect to x. \begin{equation*} f(x,y)=\int (2xy+24x)\,dx=x^{2}y+12x^{2}+h(y) \end{equation*}
where the “constant of integration,” h(y), is a function of y. Now we differentiate f with respect to y, obtaining \begin{equation*} \dfrac{\partial f}{\partial y}=\dfrac{\partial }{\partial y}[x^{2}y+12x^{2}+h(y)] =x^{2}+h' (y) \end{equation*}
999
But \dfrac{\partial f}{\partial y}=x^{2}+16, so h' (y)=16. Now we integrate h' with respect to y; then h(y)=16y+K
where K is a constant. So, f(x,y)=x^{2}y+12x^{2}+16y+K
is a potential function for \mathbf{F}.
(c) Since \mathbf{F} is independent of the path, we can use the Fundamental Theorem of Line Integrals. Since f(x,y)=x^{2}y+12x^{2}+16y + K and \mathbf{F}=\nabla\! \ f, \begin{equation*} \int_{C}\mathbf{F}\,{\cdot}\, d\mathbf{r}=\int_{C}\nabla\! \ f\,{\cdot}\, d\mathbf{r}=\big[ f(x,y)\big] _{(0,1)}^{(1,2)}=f(1,2)-f(0,1)=46-16=30 \end{equation*}
for any piecewise-smooth curve C connecting ( 0,1) to ( 1,2).
NOW WORK
EXAMPLE 7Finding a Potential Function for a Conservative Vector Field
- (a)
Show that the line integral \begin{equation*} \int_{C}\mathbf{F}\,{\cdot}\, d\mathbf{r}=\int_{C}[(y\cos x+2xe^{y})\,dx+(\sin x+x^{2}e^{y}+4)\,dy] \end{equation*}
is independent of the path.
- (b)
Find a potential function f for which \begin{equation*} \nabla\! \ f=(y\cos x+2xe^{y})\mathbf{i}+(\sin x+x^{2}e^{y}+4)\mathbf{j} \end{equation*}
Solution (a) Let P(x,y)=y\cos x+2xe^{y} and Q(x,y)=\sin x+x^{2}e^{y}+4. Then \begin{equation*} \dfrac{\partial P}{\partial y}=\cos x+2xe^{y}=\dfrac{\partial Q}{\partial x} \end{equation*}
Since P, \ Q, \ \dfrac{\partial P}{\partial y}, and \dfrac{\partial Q }{\partial x} are continuous everywhere in the xy-plane, and since \dfrac{\partial P}{\partial y}=\dfrac{\partial Q}{\partial x}, the vector field \mathbf{F}=\mathbf{F}(x,y)=(y\cos x+2xe^{y})\mathbf{i}+(\sin x+x^{2}e^{y}+4)\mathbf{j} is conservative and \int_{C}\mathbf{F}\,{\cdot}\, d\mathbf{r} is independent of the path.
(b) Since \mathbf{F} is a conservative vector field, there is a potential function f for \mathbf{F} for which \begin{equation*} \nabla\! \ f=\mathbf{F}=(y\cos x+2xe^{y})\mathbf{i}+(\sin x+x^{2}e^{y}+4)\mathbf{j} \end{equation*}
Since \nabla \! \ f=\dfrac{\partial f}{\partial x}\mathbf{i}+\dfrac{\partial f}{\partial y}\mathbf{j}, \begin{equation*} \dfrac{\partial f}{\partial x}=y\cos x+2xe^{y}\qquad \hbox{and}\qquad \dfrac{\partial f}{\partial y}=\sin x+x^{2}e^{y}+4 \end{equation*}
We integrate the function on the right partially with respect to y. Then \begin{equation*} f(x,y)=\int ( \sin x+x^{2}e^{y}+4)\, dy=y\sin x+x^{2}e^{y}+4y+k(x) \end{equation*}
in which the “constant of integration,” k(x), is a function of x. Now we differentiate f with respect to x to get \begin{equation*} \dfrac{\partial f}{\partial x}=y\cos x+2xe^{y}+k' (x) \end{equation*}
But \dfrac{\partial f}{\partial x}=y\cos x+2xe^{y}. So, \begin{eqnarray*} y\cos x+2xe^{y}&=& y\cos x+2xe^{y}+k' (x) \\[4pt] k' (x)& =&0 \end{eqnarray*}
1000
Then k(x)=K\qquad \hbox{where \(K\) is a constant}
Therefore, f(x,y)=y\sin x+x^{2}e^{y}+4y+K
is a potential function for \mathbf{F}.
NOW WORK
EXAMPLE 8Determining Whether a Line Integral Is Independent of the Path
Determine if \int_{C}(x^{2}y\,dx+xy^{2}\,dy) is independent of the path anywhere in the plane.
Solution Let P=x^{2}y and Q=xy^{2}. Then \dfrac{\partial P}{\partial y}=x^{2} and \dfrac{\partial Q}{\partial x}=y^{2}. Since these two functions are not equal (except on the graph of the equation x^{2}=y^{2}, which is not an open set), the line integral is not independent of the path anywhere in the xy-plane.
The summary below lists the important results obtained so far involving line integrals, independence of path, and conservative vector fields.
Summary
Let \mathbf{F}=\mathbf{F}(x,y)=P(x,y)\mathbf{i}+Q(x,y)\mathbf{j} be a vector field, where P and Q are two functions that are continuous on an open, connected region R containing a piecewise-smooth curve C.
- \mathbf{F} is a conservative vector field if \mathbf{F}=\nabla \ f for a function f that has continuous first-order partial derivatives.
- If \mathbf{F}=P\,\mathbf{i}+Q\,\mathbf{j} is a conservative vector field, then \int_{C}\mathbf{F}\,{\cdot}\, d\mathbf{r}=\int_{C}(P\,dx+Q\,dy) is independent of the path.
- If \int_{C}(P\,dx+Q\,dy) is independent of the path and if C is a closed curve in R, then \int_{C}\mathbf{F}\,{\cdot}\, d\mathbf{r}=\int_{C}(P\,dx+Q\,dy)=0.
- If \int_{C}(P\,dx+Q\,dy) is independent of path, then \mathbf{F}=P\, \mathbf{i}+Q\,\mathbf{j} is a conservative vector field.
- If \dfrac{\partial P}{\partial y} and \dfrac{\partial Q}{\partial x} are also continuous on R and if R is open and simply connected, then \mathbf{F} =P\,\mathbf{i}+Q\,\mathbf{j} is a conservative vector field if and only if \dfrac{\partial P}{\partial y}=\dfrac{\partial Q}{\partial x}.