15.2 Line IntegralsPrinted Page 977
OBJECTIVES
When you finish this section, you should be able to:
- Define a line integral in the plane (p. 977)
- Find the value of a line integral along a smooth curve (p. 979)
- Find line integrals of the form \boldsymbol\int_{\!\scriptsize\boldsymbol C}~\boldsymbol{f(x}, \boldsymbol{y)}\, \boldsymbol{dx} and \boldsymbol\int_{\!\scriptsize\boldsymbol C}~\boldsymbol{f(x}, \boldsymbol{y)}\, \boldsymbol{dy} (p. 981)
- Find line integrals along a piecewise-smooth curve (p. 984)
- Find the value of a line integral in space (p. 985)
NEED TO REVIEW?
Smooth curves are discussed in Section 9.2, pp. 647-648.
The value of a definite integral \int_{a}^{b}f(x)\,dx is determined by the values of the function f on the closed interval [a,b]. (See Chapter 5.) The value of a double integral \iint\limits_{\kern-3ptR}f(x,y)\,dA is determined by the values of f on a closed, bounded region R of the xy-plane, and the value of a triple integral \iiint\limits_{\kern-13ptE}f(x,y,z)\,dV is determined by the values of f on a closed, bounded solid E in space. (See Chapter 14.)
In this section, we define a line integral. The value of a line integral is determined by the values of a function f along a smooth curve C. A physical application that uses a line integral is the problem of finding the mass of a long thin piece of wire of variable density, whose shape is described by a curve C.
1 Define a Line Integral in the PlanePrinted Page 977
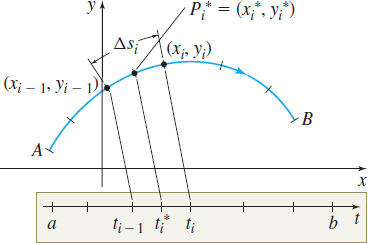
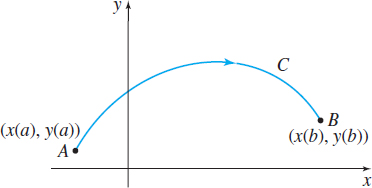
Let C be a smooth curve whose parametric equations are given by x=x(t)\quad y=y(t)\qquad a\leq t\leq b
See Figure 10. As t increases from a to b, the corresponding points (x(t),y(t)) trace out the curve C from the point A=( x(a),y(a)) to the point B=(x(b),y(b)); that is, the orientation of C is from A to B. Let z= f(x,y) be a function that is defined on some region containing the curve C.
978
We partition the closed interval [a,b] into n subintervals: \lbrack a,t_{1}],\quad \lbrack t_{1},t_{2}],\quad \ldots ,\quad \lbrack t_{i-1},t_{i}],\quad \ldots ,\quad \lbrack t_{n-1},b]
and denote the length of each subinterval by \Delta t_{1}, \Delta t_{2}, \ldots ,\Delta t_{i},\ldots , \Delta t_{n}. Then corresponding to each number a=t_{0}, t_{1}, \ldots ,t_{i},\ldots , t_{n}=b of the partition, there is a succession of points P_{0}, P_{1}, \ldots ,P_{i},\ldots , P_{n} on the curve C. These points partition the curve C into n subarcs of lengths \Delta s_{1}, \Delta s_{2}, \Delta s_{3}, \ldots ,\Delta s_{i},\ldots , \Delta s_{n}, as shown in Figure 11. We define the norm \Vert \Delta \Vert of the partition to be the length of the subarc with the largest arc length.
Now we pick a number t_{i}{}^* in each subinterval [ t_{i-1},t_{i}], i=1,2,\ldots ,n, and let P_{i}{}^*=( x_{i}{}^{*}, y_{i}{}^{*}) be the point in the ith subarc corresponding to the number t_{i}{}^*. We form the sums \sum_{i=1}^{n}f(x_{i}^{\ast },y_{i}^{\ast })\Delta s_{i}
These sums depend on both the choice of the partition of [a,b] and the choice of P_{i}^{\ast }. If all such sums can be made as close as we please to a number L by choosing partitions whose norms are sufficiently close to 0, then L is the limit of these sums as \Vert \Delta \Vert approaches 0 and we write L=\lim\limits_{\left\Vert \Delta \right\Vert \rightarrow 0}\sum\limits_{i=1}^{n}f(x_{i}^{\ast },y_{i}^{\ast })\Delta s_{i}.
DEFINITION Line Integral of f Along C
Let C be a smooth curve defined by the parametric equations x=x(t) and y=y(t), a\leq t\leq b. Let z=f(x,y) be a function defined on some region containing C. The line integral of f along C from t=a to t=b is {\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \int_{C}f(x,y)\,ds=\lim\limits_{\Vert \Delta \Vert \rightarrow 0}\sum\limits_{i=1}^{n}f(x_{i}^{\ast },y_{i}^{\ast })\Delta s_{i} }}}
provided this limit exists.
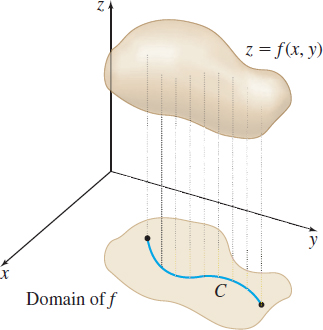
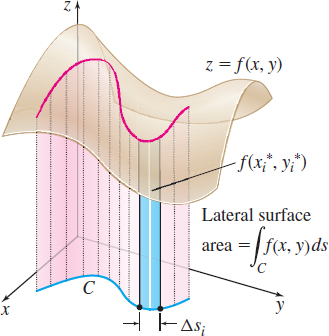
The line integral \int_{C}f(x,y)\, ds is the sum of the values of z=f(x,y) as C is traversed from t=a to t=b. See Figure 12.
We state without proof a method for finding the value of a line integral when the function f is continuous on some region that contains C.
THEOREM The Value of a Line Integral
Let C be a smooth curve defined by the parametric equations x=x(t)\quad y=y(t)\qquad a\leq t\leq b
Let z=f(x,y) be a function that is continuous on some region that contains the curve C. Then the line integral of f along C from t=a to t=b exists and \begin{equation*} {\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \int_{C}f(x,y,z)\,ds=\int_{a}^{b}f(x(t),y(t))\sqrt{\left( \dfrac{dx}{dt}\right) ^{\!\!2}+\left( \dfrac{dy}{dt} \right) ^{\!\!2}}dt }}} \tag{1} \end{equation*}
NOTE
If f(x,y) =1, the line integral of f along C is the arc length of C from t=a to t=b.
Equation (1) is the result of substituting the parametric equations x=x(t) and y=y(t) of C for x and y in f and using the arc length formula for the differential ds. This result expresses the fact that when a function is continuous on a region containing a smooth curve, then the line integral can be found using techniques for finding definite integrals.
NEED TO REVIEW?
Arc length is discussed in Section 9.2, pp. 651-653.
2 Find the Value of a Line Integral Along a Smooth CurvePrinted Page 979
979
EXAMPLE 1Finding the Value of a Line Integral Along a Smooth Curve
Find \int_{C}y\,ds if C is the curve defined by the parametric equations x(t)=t and y(t)=\sqrt{t}, 2\leq t\leq 6
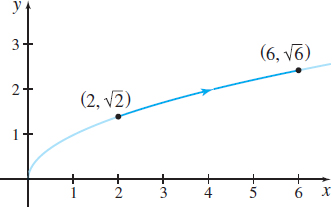
Solution The curve C is smooth and is part of the graph of y=\sqrt{x}, from (2,\sqrt{2}) to (6,\sqrt{6}), as shown in Figure 13.
The differential ds of arc length along C is given by ds=\sqrt{\left( \dfrac{dx}{dt}\right) ^{2}+\left( \dfrac{dy}{dt}\right) ^{2}}\,dt
Since \dfrac{dx}{dt}=1 and \dfrac{dy}{dt}=\dfrac{1}{2\sqrt{t}}, we have ds=\sqrt{1^{2}+\left( \dfrac{1}{2\sqrt{t}}\right) ^{2}}\,dt=\sqrt{1+\dfrac{1}{4t}}\,dt=\sqrt{\dfrac{4t+1}{4t}}\,dt=\dfrac{\sqrt{4t+1}}{2\sqrt{t}}\,dt
Now we use formula (1). \int_{C}y\,ds\underset{\underset{\color{#0066A7}{\hbox{\(y=\sqrt{t}\)}}}{\color{#0066A7}{\uparrow}}}{=}\int_{2}^{6}\sqrt{t}\dfrac{\sqrt{4t+1}}{2\sqrt{t}}\,dt=\dfrac{1}{2}\int_{2}^{6}\sqrt{4t+1}\,dt=\dfrac{1}{2}\left[ \dfrac{(4t+1)^{3/2}}{4\,{\cdot}\, \dfrac{3}{2}}\right] _{2}^{6}=\dfrac{49}{6}
NOW WORK
It can be shown that the value of the line integral along a smooth curve C does not depend on the parametric representation of the curve; any pair of parametric equations with the same orientation satisfying the assumptions of the Value of a Line Integral Theorem will give the same value.
EXAMPLE 2Finding the Value of a Line Integral
Find \int_{C}(x^{2}+y)\,ds
if C is the line segment from (0,0) to (1,2) and C is expressed using the parametric equations:
- (a) x(t) =t and y(t) =2t,\quad 0\leq t\leq 1
- (b) x(t) =\sin t and y(t) =2\sin t,\quad 0\leq t\leq \dfrac{\pi }{2}
Solution The two sets of parametric equations in (a) and (b) are just different ways of representing a part of the line y=2x from (0,0) to (1,2), as shown in Figure 14.
(a) For x(t) =t and y(t) =2t, we have \dfrac{dx}{dt}=1 and \dfrac{dy}{dt}=2. The differential ds of the arc length s is ds=\sqrt{1^{2}+2^{2}}dt=\sqrt{5}\,dt. Then \int_{C}(x^{2}+y)\,ds \underset{ \underset{ \underset{\color{#0066A7} {\hbox{\(y=2t\)}}} {\color{#0066A7}{\hbox{\(x=t\)}}}} {\color{#0066A7}{\uparrow }}} {=} \int_{0}^{1}(t^{2}+2t)\sqrt{5}\,dt=\left[\sqrt{5}\left( \dfrac{t^{3}}{3} +t^{2}\right) \right] _{0}^{1}=\dfrac{4\sqrt{5}}{3}
980
(b) For x(t) =\sin t and y(t) =2\sin t, we have \dfrac{dx}{dt}=\cos t and \dfrac{dy}{dt}=2\cos t. Since \cos t\geq 0 on 0\leq t\leq \dfrac{\pi }{2}, the differential ds of the arc length s is ds=\sqrt{\left( \dfrac{dx}{dt}\right) ^{2}+\left( \dfrac{dy}{dt}\right) ^{2}} \,dt=\sqrt{\cos ^{2}t+4\cos ^{2}t}\,dt=\sqrt{5\cos ^{2}t}\,dt=\sqrt{5}\cos t\,dt
Then \begin{eqnarray*} \int_{C}(x^{2}+y)\,ds \underset{\underset{\underset{\color{#0066A7}{\hbox{\(y=2\sin t\)}}}{\color{#0066A7}{\hbox{\(x=\sin t\)}}}} {\color{#0066A7}{\uparrow }}}{=}\int_{0}^{\pi /2}(\sin ^{2}t+2\sin t)\sqrt{5}\cos t\,dt= \sqrt{5}\int_{0}^{\pi /2}(\sin ^{2}t+2\sin t)\cos t\,dt \\[-10pt] =\sqrt{5}\left[ \dfrac{\sin ^{3}t}{3}+\sin ^{2}t\right] _{0}^{\pi /2}=\dfrac{4\sqrt{5}}{3} \end{eqnarray*}
the same value found in (a).
NOW WORK
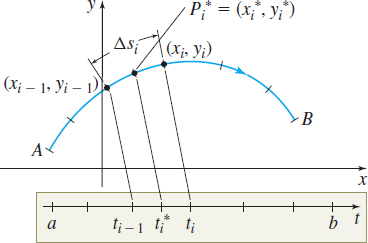
The mass of a long thin wire of variable density, whose shape is described by a smooth curve C, can be found using a line integral. Suppose C is a smooth curve defined by the parametric equations x=x(t) , y=y(t) , for a\leq t\leq b. Suppose the variable mass density (mass per unit length) at the point (x,y) on C is \rho =\rho (x,y) , where \rho is continuous on some region containing C. We partition [a,b] into n subintervals [ t_{i-1},t_{i}] , for i=1,2,\ldots ,n. In each subinterval [ t_{i-1},t_{i}] , we choose a number t_{i}{}^*, as shown in Figure 15. Then the mass \Delta M_{i} of the corresponding short piece of wire between ( x_{i-1},y_{i-1}) and (x_{i}, y_{i}) is \Delta M_{i}\approx \rho ( x_{i}{}^{*},y_{i}{}^{*}) \Delta s_{i}, where \Delta s_{i} is the length of the short piece of wire and ( x_{i}{}^{*},y_{i}{}^{*}) is the point corresponding to t_{i}{}^*. We define the norm \Vert \Delta \Vert of the partition to be largest length \Delta s_{i}. The sums {\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \sum\limits_{i=1}^{n} \Delta M_i= \sum\limits_{i=1}^{n}\rho (x_{i}^{\ast },y_{i}^{\ast })\Delta s_{i} }}}
over all the subintervals approximate the mass M of the wire. By taking the limit of these sums as the norm \Vert \Delta \Vert approaches 0, we obtain the mass M of the wire \begin{equation*} {\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ M=\int_{C}\rho (x,y)\,ds }}} \tag{2} \end{equation*}
EXAMPLE 3Finding the Mass of a Wire with Variable Density
Find the mass M of a thin piece of wire in the shape of a semicircle x=2\cos t, y=2\sin t, 0\leq t\leq \pi , if the variable density of the wire is \rho (x,y)=y+2.
Solution Using (2), we find that the mass M of the wire is \begin{eqnarray*} M&=&\int_{C}\rho (x,y)\,ds=\int_{C}(y+2)\,ds=\int_{0}^{\pi }(y+2) \sqrt{\left( \dfrac{dx}{dt}\right) ^{2}+\left( \dfrac{dy}{dt}\right) ^{2}}dt\\[4pt] &=& \int_{0}^{\pi }(2\sin t+2)\sqrt{(-2\sin t)^{2}+(2\cos t)^{2}}\,dt \hspace{1.5pc}\color{#0066A7}{\dfrac{dx}{dt} =-2\sin t; \dfrac{dy}{dt} =2 \cos t}\\ &=&\int_{0}^{\pi }4(\sin t+1) \,dt=4\big[-\cos t+t\big]_{0}^{\pi }=4[\pi +2] \end{eqnarray*}
NOW WORK
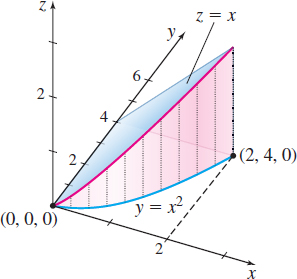
Line integrals also have a geometric application. In Figure 16, the surface z=f(x,y) lies above the xy-plane, so f(x,y) \geq 0. Suppose C is a smooth curve that lies in the xy-plane within the domain of f. If we draw lines parallel to the z-axis, from C to the surface, the result is a cylinder, and its area is called the lateral surface area of the cylinder.
981
EXAMPLE 4Finding the Lateral Surface Area of a Cylinder
Find the lateral surface area A of the cylinder that lies above the xy-plane, below the surface z = f(x,y)=x, and formed by lines parallel to the z -axis that intersect the curve y=x^{2}, 0\leq x\leq 2.
Solution Figure 17 illustrates the cylinder. Along C, y=x^{2}, the differential ds of arc length is ds=\sqrt{1+\left( \dfrac{dy}{dx}\right) ^{2}}\,dx\underset{ \underset{\color{#0066A7} {\hbox{\(\dfrac{dy}{dx}=2x\)}}} {\color{#0066A7}{\uparrow }}}{=} \sqrt{1+4x^{2}}\,dx\\[-11pt]
The lateral surface area A of the cylinder is \begin{eqnarray*} A& =&\int_{C}f(x,y) ds=\int_{C}x\,ds=\int_{0}^{2}x\sqrt{1+4x^{2}} \,dx \qquad \color{#0066A7}{{\rm Let}\ u=1+4x^{2};\ {\rm then}\ du=8x\,dx\ {\rm or} \ x\,dx= \dfrac{1}{8}\, du.}\\ && \hspace{14.5pc}\color{#0066A7}{\hbox{When \(x=0\), \(u=1\); when \(x=2\), \(u=17\).}} \\ & =&\int_{1}^{17}\dfrac{1}{8}\sqrt{u}\,du=\left[ \dfrac{1}{4}\dfrac{u^{3/2}}{3}\right] _{1}^{17}=\dfrac{17\sqrt{17}-1}{12} \end{eqnarray*}
NOW WORK
3 Find Line Integrals of the Form ∫Cf(x,y) dx and ∫Cf(x,y) dy
Printed Page 981
Consider a function f of two variables x and y. When we introduced partial derivatives, we said that the partial derivative f_{x}(x,y) of a function z=f(x,y) is found by treating y as a constant (\Delta y=0) and differentiating z=f(x,y) with respect to x; similarly, f_{y}(x,y) is found by holding x fixed (\Delta x=0) and differentiating f with respect to y.
For a line integral \int_{C}f(x,y)\, ds, the differential ds of arc length along the smooth curve C is (ds) ^{2}=(dx) ^{2}+(dy) ^{2}. If we treat y as a constant, then dy=0, ds=dx, and we have the line integral along C with respect to x, \int_{C}f(x,y)\, dx. Similarly, if x is treated as a constant, then dx=0, ds=dy, and we have the line integral along C with respect to y, \int_{C}f(x,y)\, dy.
These line integrals can be expressed as definite integrals if C is a smooth curve and if the function f is continuous on a region that contains C.
THEOREM The Value of a Line Integral Along C with Respect to x or y
Let C be a smooth curve defined by the parametric equations \begin{equation*} x=x(t)\quad y=y(t)\qquad a\leq t\leq b \end{equation*}
Let f=f(x,y) be a function that is continuous on some region that contains the curve C. Then the line integral of f along C with respect to x is given by \begin{equation*} {\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \int_{C}f(x,y)\,dx=\int_{a}^{b}f(x(t),y(t))x' (t)\,dt }}} \tag{3} \end{equation*}
and the line integral of f along C with respect to y is given by \begin{equation*} {\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \int_{C}f(x,y)\,dy=\int_{a}^{b}f(x(t),y(t))y' (t)\,dt }}} \tag{4} \end{equation*}
In general, each of these line integrals has a different value.
982
EXAMPLE 5Finding a Line Integral Along C with Respect to x and with Respect to y
Find \int_{C}(x-3y)\,dx\qquad\hbox{and}\qquad \int_{C}(x-3y)\,dy
if C is the part of the parabola x=y^{2} that joins the points (1,1) and (4,2).
Solution The function f(x,y) =x-3y is continuous, and C is a smooth curve everywhere in the plane. So, we can use the formulas (3) and (4). Using the parametric equations of the curve C, x=t^{2} and y=t, \ 1\leq t\leq 2, we find dx=2t\,dt and dy=dt. Then \begin{eqnarray*} \int_{C}(x-3y)\,dx &=&\int_{1}^{2}(t^{2}-3t)2t\,dt=2\int_{1}^{2}(t^{3}-3t^{2}) dt=-\dfrac{13}{2} \notag \\[4pt] \int_{C}(x-3y)\,dy &=&\int_{1}^{2}(t^{2}-3t)\,dt=-\dfrac{13}{6} \end{eqnarray*}
NOW WORK
It is not always necessary to use parametric equations for C when finding the value of the line integral of a function f. For example, if a smooth curve C is given by the rectangular equation y=g(x), a\leq x\leq b, then parametric equations of C are \begin{equation*} x=t\quad y=g(t)\qquad a\leq t\leq b \end{equation*}
Since dx=dt and dy=g' (t)\,dt, we have \begin{eqnarray*} \int_{C}f(x,y)\,dx& =&\int_{a}^{b}f(t,g(t))\,dt=\int_{a}^{b}f(x,g(x))\,dx \\[4pt] \int_{C}f(x,y)\,dy& =&\int_{a}^{b}f(t,g(t))g' (t)\,dt=\int_{a}^{b}f(x,g(x))g' (x)\,dx \end{eqnarray*}
For example, consider the curve C in Example 5. C has the rectangular equation y=\sqrt{x}, 1\leq x\leq 4. Then \begin{eqnarray*} \int_{C}(x-3y)\,dx &\underset{ \underset{\color{#0066A7} {\hbox{\(y=\sqrt{x}\)}}} {\color{#0066A7}{\uparrow }}}{=}&\int_{1}^{4}(x-3\sqrt{x})\,dx=-\dfrac{13}{2}\\ \int_{C}(x-3y)\,dy &\underset{ \underset{ \underset{\color{#0066A7} {\hbox{\(dy=\dfrac{1}{2\sqrt{x}}\,dx\)}}} {\color{#0066A7}{\hbox{\(y=\sqrt{x}\)}}}} {\color{#0066A7}{\uparrow }}} {=}&\int_{1}^{4}(x-3\sqrt{x})\left( \dfrac{1}{2\sqrt{x}}\right) dx=-\dfrac{13}{6} \end{eqnarray*}
In many applications, we combine the two line integrals \int_{C}P(x,y)\, dx and \int_{C}Q(x,y)\, dy using the notation \int_{C}(P\,dx+Q\,dy) .
DEFINITION Line Integral \int_{C} (P\,dx+Q\,dy) Along a Smooth Curve C
Let C denote a smooth curve, and let P=P(x,y) and Q=Q(x,y) be functions of two variables that are continuous on some region containing C . The line integral of P\,dx+Q\,dy along C is defined as {\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \int_{C}(P\,dx+Q\,dy)=\int_{C}P(x,y)\,dx+\int_{C}Q(x,y)\,dy }}}
983
EXAMPLE 6Finding a Line Integral of the Form \int_{C}( P\,dx+Q\,dy)
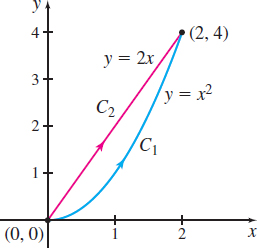
Find the line integral \int_{C}(y^{2}\,dx-x^{2}\,dy) along
C_{1}: The parabola y=x^{2} joining the two points (0,0) and (2,4)
C_{2}: The line y=2x joining the two points (0,0) and (2,4)
Solution The curves C_{1} and C_{2} are smooth, and the functions P(x,y) =y^{2} and Q(x,y) = -x^{2} are continuous in the xy-plane.
Along C_{1}, parametric equations for the parabola are x(t) =t, y(t) =t^{2}. Then dx=dt and dy=2t\,dt, so \begin{eqnarray*} \int_{C_{1}}(y^{2}\,dx-x^{2}\,dy)&=&\int_{C_{1}}y^{2}\,dx-\int_{C_{1}}x^{2}\,dy=\int_{0}^{2}(t^2) ^{2}\,dt-\int_{0}^{2}t^{2}(2t\,dt)\\ &=& \int_{0}^{2}t^{4}\,dt-2\int_{0}^{2}t^{3}\,dt=\left[ \dfrac{t^{5}}{5}\right] _{0}^{2}-\left[ \dfrac{t^{4}}{2}\right] _{0}^{2}=-\dfrac{8}{5} \end{eqnarray*}
Along C_{2}, parametric equations for the line segment are x(t) =t, y(t) =2t. Then dx=dt and dy=2\,dt, so \begin{eqnarray*} \int_{C_{2}}(y^{2}\,dx-x^{2}\,dy)&=&\int_{C_{2}}y^{2}\,dx-\int_{C_{2}}x^{2}\,dy=\int_{0}^{2}(2t) ^{2}\,dt-\int_{0}^{2}t^{2}(2\,dt)\\[4pt] &=& \left[ \dfrac{4t^{3}}{3}\right] _{0}^{2}-\left[ \dfrac{2t^{3}}{3}\right] _{0}^{2}=\dfrac{16}{3} \end{eqnarray*}
Figure 18 shows the curves C_{1} and C_{2} joining the points ( 0,0) and (2,4) .
NOW WORK
Observe that the value of the line integral in Example 6 depends on the curve C over which the integration takes place. In the next section, we investigate conditions under which the value of the integral is independent of the curve taken, that is, conditions under which the value of the integral depends only on the endpoints of the curve.
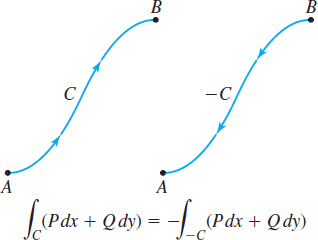
The orientation of the curve C also plays a role in the value of a line integral over C. If C is a smooth curve, then -C is the same curve but with the reverse orientation. Then {\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \int_{C}(P\,dx+Q\,dy)=-\int_{-C}(P\,dx+Q\,dy) }}}
That is, reversing the orientation of the curve C alters the value of the line integral by a factor of -1. See Figure 19.
The line integral \int_{C}(P\,dx+Q\,dy) can be written compactly using vectors. Suppose \mathbf{F}=\mathbf{F}(x,y)=P(x,y)\mathbf{i}+Q(x,y)\mathbf{j}
NEED TO REVIEW?
The dot product is discussed in Section 10.4, pp. 715-716.
is a vector field that is continuous on some region containing the smooth curve C traced out by \mathbf{r}=\mathbf{r}(t)=x(t)\mathbf{i}+y(t)\mathbf{j}, a\leq t\leq b. Then d\mathbf{r}=dx\mathbf{i}+dy\mathbf{j} and the dot product \mathbf{F}\,{\boldsymbol\cdot}\, d\mathbf{r} is \begin{equation*} \mathbf{F}\,{\boldsymbol\cdot}\, d\mathbf{r}=\left[ P(x,y)\mathbf{i}+Q(x,y)\mathbf{j}\right] \,{\boldsymbol\cdot}\, \left[ dx\mathbf{i}+dy\mathbf{j}\right] =P(x,y) \,dx+Q(x,y) \,dy \end{equation*}
So, {\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \int_{C}\mathbf{F}\,{\boldsymbol\cdot}\, d\mathbf{r}=\int_{C}(P\,dx+Q\,dy) }}}
984
EXAMPLE 7Finding a Line Integral of the Form \int_{C}\mathbf{F}\,{\boldsymbol\cdot}\, d\mathbf{r}
Find \int_{C}\mathbf{F}\,{\boldsymbol\cdot}\, d\mathbf{r}
if \mathbf{F}(x,y)=x\mathbf{i}+xy\mathbf{j} and the curve C is traced out by the vector function \mathbf{r}(t)=t\,\mathbf{i}\,+\,t^{2} \mathbf{j}, 0\leq t\leq 2.
Solution Parametric equations of the curve C are x(t) =t\qquad y(t) =t^{2}\qquad 0\leq t\leq 2
So, \mathbf{F}=x\mathbf{i}+xy\,\mathbf{j}=t\mathbf{i}+(t) (t^{2}) \mathbf{j}=t\mathbf{i}+t^{3}\mathbf{j}
and d\mathbf{r}=\dfrac{d\mathbf{r}}{dt}\,dt=\dfrac{d}{dt}( t\,\mathbf{i} +t^{2}\mathbf{j})\, dt=(\mathbf{i}+2t\mathbf{j})\,dt
Then \mathbf{F}\,{\boldsymbol\cdot}\, d\mathbf{r}=( t\mathbf{i}+t^{3}\,\mathbf{j}) \,{\boldsymbol\cdot}\, ( \mathbf{i}+2t\,\mathbf{j}) \,dt=( t+2t^{4}) \,dt
so that \int_{C}\mathbf{F}\,{\boldsymbol\cdot}\, d\mathbf{r}=\int_{0}^{2}(t+2t^{4}) \,dt=\dfrac{74}{5}
NOW WORK
4 Find Line Integrals Along a Piecewise-Smooth CurvePrinted Page 984
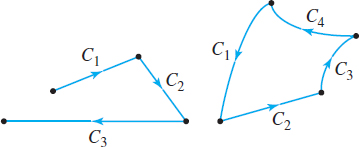
The definition of a line integral of f along C assumes that C is a smooth curve. That is, the parametric equations x(t) and y(t) defining C have derivatives \dfrac{dx}{dt} and \dfrac{dy}{dt} that are continuous and are never simultaneously 0 on a\leq t\leq b. If a curve C is not smooth, but consists of a finite number of smooth curves, say, C_{1},\,C_{2},\ldots ,C_{n}, n\geq 2, that are joined together end to end, then C is a piecewise-smooth curve. Figure 20 shows two piecewise-smooth curves.
DEFINITION Line Integral \int_{C} (P\,dx+Q\,dy) Along a Piecewise-Smooth Curve C
Let C be a piecewise-smooth curve consisting of n\geq 2 smooth curves C_{1}, C_{2}, \ldots , C_{n}. Let P=P(x,y) and Q=Q(x,y) be functions of two variables that are each continuous on some region containing C. The line integral \int_{C}( P\,dx+Q\,dy) along C is defined as {\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \int_{C}(P\,dx+Q\,dy)=\int_{C_{1}}(P\,dx+Q\,dy)+\int_{C_{2}}(P\,dx+Q\,dy)+ \cdots +\int_{C_{n}}(P\,dx+Q\,dy) }}}
If \mathbf{F}=P\mathbf{i}+Q\mathbf{j} and C is traced out by \mathbf{r} =\mathbf{r}(t) =x(t) \mathbf{i}+y(t) \mathbf{j}, a\leq t\leq b, then {\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \int_{C}\mathbf{F}\,{\cdot}\, d\mathbf{r}=\int_{C_{1}}\mathbf{F}\,{\cdot}\, d\mathbf{r}+\int_{C_{2}}\mathbf{F}\,{\cdot}\, d\mathbf{r}+ \cdots +\int_{C_{n}}\mathbf{F} \,{\cdot}\, d\mathbf{r} }}}
985
EXAMPLE 8Finding a Line Integral Along a Piecewise-Smooth Curve
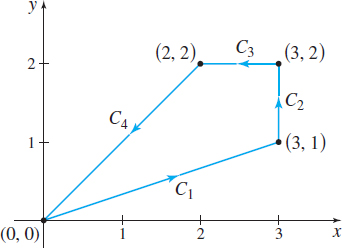
Find \int_{C}(xy\,dx+x^{2}\,dy) along the piecewise-smooth curve C illustrated in Figure 21.
Solution The values of the line integral along each of the smooth curves C_{1}, C_{2}, C_{3}, and C_{4} are \begin{eqnarray*} C_{1}{:}&& y =\dfrac{1}{3}x,\quad dy=\dfrac{1}{3}dx;\qquad 0\leq x\leq 3 \\ &&{\int_{C_{1}}(xy\,dx+x^{2}\,dy)=\int_{0}^{3}\left[ x\left( \dfrac{1}{3}x\right) dx+x^{2}\dfrac{1}{3}dx\right] =6} \\ C_{2}{:}&& x =3,\quad dx=0;\qquad 1\leq y\leq 2 \\ &&{\int_{C_{2}}(xy\,dx+x^{2}\,dy)=\int_{1}^{2}9\,dy=9} \\ C_{3}{:}&& y =2, \quad dy=0;\qquad \color{#0066A7}{\hbox{Watch the orientation here: \(x\) varies from 3 to 2.}} \\ &&{\int_{C_{3}}(xy\,dx+x^{2}\,dy)=\int_{3}^{2}2x\,dx=\left[x^{2}\right]^{2}_{3}=-5} \\ C_{4}{:}&& y =x, \quad dy=dx;\qquad \color{#0066A7}{\hbox{Watch the orientation here: \(x\) varies from 2 to 0.}} \\ &&{\int_{C_{4}}(xy\,dx+x^{2}\,dy)=\int_{2}^{0}(x^{2}\,dx+x^{2}\,dx)=2\int_{2}^{0}x^{2}dx=-\dfrac{16}{3}} \end{eqnarray*}
Then \int_{C}(xy\,dx+x^{2}\,dy)=6+9-5-\dfrac{16}{3}=\dfrac{14}{3}
NOW WORK
5 Find the Value of a Line Integral in SpacePrinted Page 985
The definition of a line integral in space is similar to that of a line integral in the plane. We state without proof the main results needed to find the value of line integrals in space.
THEOREM The Value of a Line Integral in Space
Let C be a smooth curve in space defined by the parametric equations x=x(t)\quad y=y(t)\quad z=z(t)\quad a\leq t\leq b
Let w=f(x,y,z) be a function that is continuous on some solid that contains the smooth curve C. Then the line integral of f along C from t=a to t=b exists and \begin{equation*} {\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \int_{C}f(x,y,z)\,ds=\int_{a}^{b}f(x(t),y(t),z(t) )\sqrt{\left( \dfrac{dx}{dt}\right) ^{\!\!2}+\left( \dfrac{dy}{dt} \right) ^{\!\!2}+\left( \dfrac{dz}{dt}\right) ^{\!\!2}}dt }}} \tag{5} \end{equation*}
Observe that if w=f( x,y,z) =1, then {\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \int_{C}f(x,y,z)\,ds=\int_{C}\,ds= \hbox{ arc length of \(C\) from \(a\) to \(b\)} }}}
similar to plane curves.
Suppose C is a smooth curve in space defined by the parametric equations \begin{equation*} x=x(t)\quad y=y(t)\quad z=z(t)\qquad a\leq t\leq b \end{equation*}
In space, we have line integrals along C with respect to x, with respect to y, and with respect to z. If P(x,y,z), Q(x,y,z), and R(x,y,z) are functions that are continuous
986
on some solid in space containing C, then \begin{eqnarray*} \int_{C}P(x,y,z)\,dx& =&\int_{a}^{b}P(x(t),y(t),z(t))\,x' (t)\,dt \\[4pt] \int_{C}Q(x,y,z)\,dy& =&\int_{a}^{b}Q(x(t),y(t),z(t))\,y' (t)\,dt \\[4pt] \int_{C}R(x,y,z)\,dz& =&\int_{a}^{b}R(x(t),y(t),z(t))\,z' (t)\,dt \\[4pt] \int_{C}(P\,dx+Q\,dy+R\,dz)& =&\int_{C}P\,dx+\int_{C}Q\,dy+\int_{C}R\,dz \end{eqnarray*}
If \mathbf{F}=\mathbf{F}(x,y,z)=P(x,y,z)\mathbf{i}+Q(x,y,z)\mathbf{j}+R(x,y,z)\mathbf{k} is a vector field that is continuous on some solid containing the smooth curve C: \mathbf{r}=\mathbf{r}(t)=x(t)\,\mathbf{i}+y(t)\,\mathbf{j}+z(t)\,\mathbf{k}, \ a\leq t\leq b, then the line integral of \mathbf{F \,{\boldsymbol\cdot}\, r} is {\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \int_{C}\mathbf{F}\,{\cdot}\, d\mathbf{r}=\int_{C}(P\,dx+Q\,dy+R \,dz) }}}
A curve C in space is piecewise-smooth if it consists of a finite number of smooth curves C_{1},C_{2},\ldots ,C_{n}, n\geq 2, that are joined together end to end. If C: \mathbf{r}=\mathbf{r}(t) is piecewise-smooth and if \mathbf{F}=\mathbf{F}(x,y,z) is a vector field that is continuous on some solid containing C, then {\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \int_{C}\mathbf{F}\,{\boldsymbol\cdot}\, d\mathbf{r}=\int_{C_{1}}\mathbf{F}\,{\boldsymbol\cdot}\, d \mathbf{r}+\int_{C_{2}}\mathbf{F}\,{\boldsymbol\cdot}\, d\mathbf{r}+\cdots +\int_{C_{n}} \mathbf{F}\,{\boldsymbol\cdot}\, d\mathbf{r} }}}
EXAMPLE 9Finding a Line Integral in Space
Find \int_{C}\mathbf{F}\,{\boldsymbol\cdot}\, d\mathbf{r} if \begin{equation*} \mathbf{F}(x,y,z)=xy^{2}\,\mathbf{i}+x^{2}z\,\mathbf{j}-(y-x)\,\mathbf{k} \end{equation*}
and the curve C is traced out by \mathbf{r}(t)=t\,\mathbf{i}+t^{2}\mathbf{j}+t^{3}\,\mathbf{k}, \ 0\leq t\leq 1.
Solution Parametric equations of the curve C are \begin{equation*} x=t\qquad y=t^{2}\qquad z=t^{3}\qquad 0 \le t \le 1 \end{equation*}
So, \mathbf{F}=xy^{2}\,\mathbf{i}+x^{2}z\,\mathbf{j}-(y-x)\,\mathbf{k}=t^{5} \mathbf{i}+t^{5}\mathbf{j}-(t^{2}-t)\,\mathbf{k}
and d\mathbf{r}=\dfrac{d\mathbf{r}}{dt}\,dt=(\mathbf{i}+2t\mathbf{j}+3t^{2} \mathbf{k})\,dt
Then \begin{eqnarray*} \mathbf{F}\,{\cdot}\, d\mathbf{r}&=&[ t^{5}\mathbf{i}+t^{5}\,\mathbf{j} -(t^{2}-t)\,\mathbf{k}] \,{\cdot}\, ( \mathbf{i}+2t\,\mathbf{j}+3t^{2}\, \mathbf{k}) \,dt=[ t^{5}+2t^{6}-3t^{2}(t^{2}-t)] \,dt\\ &=&( 2t^{6}+t^{5}-3t^{4}+3t^{3}) \,dt \end{eqnarray*}
so that \int_{C}\mathbf{F}\,{\boldsymbol\cdot}\, d\mathbf{r}=\int_{0}^{1}(2t^{6}+t^{5}-3t^{4}+3t^{3}) \,dt=\dfrac{253}{420}
NOW WORK
Sections 15.3–15.5 primarily treat line integrals in the plane. We continue the study of line integrals in space in Section 15.9.