13.1 Directional Derivatives; GradientsPrinted Page 863
863
OBJECTIVES
When you finish this section, you should be able to:
1 Find the Directional Derivative of a Function of Two VariablesPrinted Page 863
Recall that the partial derivatives of a function z=f(x,y) at the point (x0,y0) are defined as fx(x0,y0)=lim
where (x_{0},y_{0}) is an interior point of the domain of f. The partial derivative f_{x}(x_{0},y_{0}) equals the rate of change of f at (x_{0},y_{0}) in the direction of the positive x-axis, and the partial derivative f_{y}(x_{0},y_{0}) equals the rate of change of f at (x_{0},y_{0}) in the direction of the positive y- axis. The directional derivative of f equals the rate of change of f at (x_{0},y_{0}) in any direction in the xy -plane.
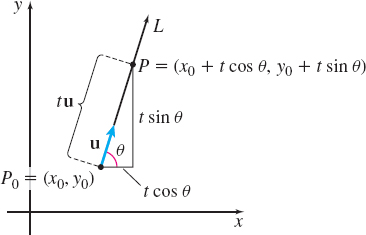
To lay the groundwork for defining the directional derivative, we consider a function z=f( x,y) whose graph is a surface in space. In Figure 1, P_{0}=(x_{0},y_{0}) is an interior point in the domain of f, and \mathbf{u}=\cos \theta \mathbf{i}+\sin \theta \mathbf{j} is a unit vector in the xy-plane with its initial point at P_{0} making an angle \theta, 0\leq \theta \leq 2\pi, with the positive x-axis.
NEED TO REVIEW?
Unit vectors are discussed in Section 10.3, pp. 708-709.
The vector \mathbf{u} allows us to move away from P_{0} in any direction. Now draw a directed line segment L with initial point P_{0} in the direction of \mathbf{u}, and choose a point P=(x,y) on L different from P_{0}, so that the directed line segment \overrightarrow{ P_{0}P} is in the domain of f. Then \overrightarrow{P_{0}P}=t\mathbf{u} for some t and the coordinates of P are (x_{0}+t\cos \theta ,y_{0}+t\sin \theta ).
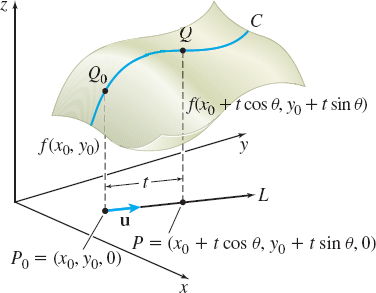
In Figure 2, we have drawn a surface z=f( x,y) and have labeled the points on the surface corresponding to P_{0}=( x_{0},y_{0}, 0), namely Q_{0}=( x_{0},y_{0},f( x_{0},y_{0}) ), and to P=( x_{0}+t\cos \theta, y_{0}+t\sin \theta, 0), namely Q=(x_{0}+t\cos \theta, y_{0}+t\sin \theta, f ( x_{0}+t\cos \theta ,y_{0}+t\sin \theta)). The average rate of change of z with respect to t in the direction of \mathbf{u}=\cos \theta \mathbf{i} +\sin \theta \mathbf{j} is \dfrac{\Delta z}{\Delta t}=\frac{f(x_{0}+t\cos \theta ,y_{0}+t\sin \theta)-f(x_{0},y_{0})}{t}
By taking the limit as t\rightarrow 0, we obtain the rate of change of f at (x_{0},y_{0}) in the direction of \mathbf{u}, provided the limit exists. This limit, denoted by D_{\mathbf{u}}f(x_{0},y_{0}), is the directional derivative of f at (x_{0},y_{0}) in the direction of \mathbf{u}.
DEFINITION Directional Derivative of a Function of Two Variables
Suppose z=f(x,y) is a function of two variables whose domain is D and (x_{0},y_{0}) is an interior point of D. If \mathbf{u}=\cos \theta \mathbf{i}+\sin \theta \mathbf{j}, 0\leq \theta \leq 2\pi, is a unit vector, the directional derivative of f at (x_{0},y_{0}) in the direction of \mathbf{u} is the number \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED]{D_{\mathbf{u}}f(x_{0},y_{0})=\lim\limits_{t \rightarrow 0}\dfrac{f(x_{0}+t\cos \theta ,y_{0}+t\sin \theta )-f(x_{0},y_{0})}{t}}}
provided the limit exists.
There are an infinite number of directions from P_{0} and so there are an infinite number of directional derivatives of f at the point ( x_{0},y_{0}). The directional derivative D_{\mathbf{u}}f( x_{0},y_{0}) depends not only on the point ( x_{0},y_{0}), but also on the angle \theta, the direction taken from ( x_{0},y_{0}). The partial derivatives f_{x} and f_{y} of f at (x_{0},y_{0}) are special cases of the directional derivative D_{\mathbf{u}}f(x_{0},y_{0}), where the direction taken is {\bf i} for f_{x}(x_{0},y_{0}) and the direction taken is {\bf j} for f_{y}(x_{0},y_{0}). For example, if \theta =0, then \begin{equation*} \mathbf{u}=\cos 0\; \mathbf{i}+\sin 0\;\mathbf{j}=\mathbf{i} \end{equation*}
864
Then using the definition of the directional derivative of f at (x_{0},y_{0}) in the direction \mathbf{u} =\mathbf{i}, we find \begin{equation*} D_{\mathbf{u}}f(x_{0},y_{0})=D_{{\bf i}}f(x_{0},y_{0})\underset{\color{#0066A7}{\theta =0}}{\underset{\color{#0066A7}{\uparrow} }{=}}\lim_{t\rightarrow 0}\frac{ f(x_{0}+t,y_{0})-f(x_{0},y_{0})}{t}=f_{x}(x_{0},y_{0}) \end{equation*}
Similarly, if \theta =\dfrac{\pi }{2}, then \begin{equation*} \mathbf{u=}\cos \dfrac{\pi }{2}\mathbf{i}+\sin \dfrac{\pi }{2}\mathbf{j}= \mathbf{j} \end{equation*}
and \begin{equation*} D_{{\bf j}}f(x_{0},y_{0})=f_{y}(x_{0},y_{0}) \end{equation*}
NEED TO REVIEW?
Conditions under which a function z=f(x,y) is differentiable are discussed in Section 12.4, pp. 841-843.
Finding directional derivatives using the definition can be challenging. However, for functions z=f(x,y) that are differentiable, we can use the formula below to find directional derivatives.
THEOREM Directional Derivative of a Differentiable Function f
If z=f(x,y) is a differentiable function, then the directional derivative of f at (x_{0},y_{0}) in the direction of the unit vector \mathbf{u}=\cos \theta \mathbf{i}+\sin \theta \mathbf{j} is given by \begin{equation} \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED]{ D_{\mathbf{u}}f(x_{0},y_{0})=f_{x}(x_{0},y_{0})\cos \theta +f_{y}(x_{0},y_{0})\sin \theta }} \end{equation}
Proof
If x=x_0\,+\,t\cos \theta, y=y_0\,+\,t\sin \theta, and \theta is fixed, we can express z=f( x,y) as a function z= f(x_{0}+t \cos \theta, y_{0} + t \sin\theta)=g(t). Then the derivative of g at t=0 is \begin{eqnarray} g′ (0) &=& \lim\limits_{t\rightarrow 0}\dfrac{g(t)-g(0) }{t-0}=\lim_{t\rightarrow 0}\frac{f(x_{0}+t\cos \theta ,y_{0}+t\sin \theta )-f(x_{0},y_{0})}{t}\nonumber \\ &=& D_{\mathbf{u}}f(x_{0},y_{0}) \end{eqnarray}
Because f is differentiable, we can use Chain Rule I to find g′(t). \begin{eqnarray*} g′ (t) &=&\frac{\partial f}{\partial x}\frac{dx}{dt}+\frac{\partial f}{ \partial y}\frac{dy}{dt} \qquad \color{#0066A7}{\hbox{Chain Rule I.}} \\ &=&\frac{\partial f}{\partial x}\cos \theta +\frac{\partial f}{\partial y} \sin \theta \quad\! \color{#0066A7}{\dfrac{dx}{dt}=\dfrac{d}{dt} (x_{0}+t\cos \theta ) = \cos \theta ; \dfrac{dy}{dt}=\dfrac{d}{dt} (y_{0}+t\sin \theta ) =\sin \theta} \end{eqnarray*}
If t=0, then x=x_{0} and y=y_{0}, and g′ (0)=f_{x}(x_{0},y_{0})\cos \theta +f_{y}(x_{0},y_{0})\sin \theta \underset{\color{#0066A7}{(2)}}{\underset{\color{#0066A7}{\uparrow} }{=}}D_\mathbf{u}f( x_{0},y_{0})
EXAMPLE 1Finding the Directional Derivative of a Function
- (a) Find the directional derivative D_{\mathbf{u}}f(x,y) of f(x,y)=x^{2}y+y^{2} in the direction of \mathbf{u}=\cos \dfrac{\pi }{4} \mathbf{i}+\sin \dfrac{\pi }{4}\mathbf{j}.
- (b) What is D_{\mathbf{u}}f(1,2)?
- (c) Interpret D_{\mathbf{u}}f(1,2).
865
Solution (a) Since the partial derivatives of f, namely, f_{x}(x,y)=2xy\qquad \hbox{and}\qquad f_{y}(x,y)=x^{2}+2y
are continuous, the function f is differentiable. So, we can use formula (1) with the unit vector \mathbf{u}=\cos \dfrac{\pi }{4}\mathbf{i}+\sin \dfrac{\pi }{4}\mathbf{j} =\dfrac{\sqrt{2}}{2}\mathbf{i}+\dfrac{\sqrt{2}}{2 }\mathbf{j}. Then \begin{eqnarray*} D_{\mathbf{u}}f(x,y)& =&f_{x}(x,y)\cos \theta +f_{y}(x,y)\sin \theta \\ &=& 2xy\cos \dfrac{\pi }{4}+(x^{2}+2y)\sin \dfrac{\pi }{4} \qquad \color{#0066A7}{f_x(x,y)=2xy;} \\ &&\hspace{11.50pc}\color{#0066A7}{f_y (x,y)=x^{2}+2y;\theta =\dfrac{\pi }{4}} \\ &=& \sqrt{2}xy+\dfrac{\sqrt{2}}{2}(x^{2}+2y) \end{eqnarray*}
(b) D_{\mathbf{u}}f(1,2)=2\sqrt{2}+\dfrac{\sqrt{2}}{2}(1+4)=\dfrac{9\sqrt{2}}{2}.
(c) When we are at the point ( 1,2) and moving in the direction \mathbf{u}=\dfrac{\sqrt{2}}{2}\mathbf{i}+\dfrac{\sqrt{2}}{2} \mathbf{j}, the function is changing at a rate of approximately 6.364 units per unit length.
NOW WORK
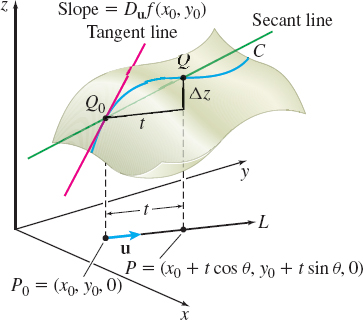
There is another (geometric) interpretation for a directional derivative. Look at Figure 3. If P_{0}=(x_{0}, y_{0},0) is an interior point in the domain of z= f(x,y), then the point Q_{0}=( x_{0}, y_{0}, z_{0}) = (x_{0}, y_{0}, f(x_{0}, y_{0})) is a point on the surface of z. As we move in the domain of f along the line L in the direction of \mathbf{u}, points are traced out on a curve C that lie on the surface z=f( x,y). This curve C is the intersection of the surface and the plane perpendicular to the xy-plane that contains the line L. It follows that for any point P=(x_{0}+t\cos \theta ,y_{0}+t\sin \theta, 0 ) on L that is in the domain of f, there is a corresponding point Q on C. Furthermore, the expression \frac{f(x_{0}+t\cos \theta ,y_{0}+t\sin \theta )-f(x_{0},y_{0})}{t} \qquad t\neq 0
equals the slope of the secant line containing the two points Q_{0} and Q on C, and the limit as t\rightarrow 0 is the slope of the tangent line to C at Q_{0}. This proves the following result.
THEOREM The Directional Derivative as a Slope
If z=f(x,y) is a differentiable function, then the directional derivative D_{\mathbf{u}}f(x_{0},y_{0}) of f at (x_{0},y_{0}) in the direction of \mathbf{u} equals the slope of the tangent line to the curve C at the point ( x_{0}, y_{0}, f(x_{0}, y_{0})) on the surface z=f( x,y), where C is the intersection of the surface with the plane perpendicular to the xy-plane and containing the line through ( x_{0}, y_{0}, 0) in the direction \mathbf{u}.
NOTE
The unit vector \mathbf{u} in the direction of a given vector is defined in Section 10.3, p. 708.
EXAMPLE 2Interpreting the Directional Derivative as a Slope
Find the directional derivative of f(x,y)=x\sin y at the point \left( 2, \dfrac{\pi }{3}\right) in the direction of \mathbf{a}=3\mathbf{i}+4 \mathbf{j}. Interpret the result as a slope.
Solution To find a directional derivative of a function f in the direction of \mathbf{a}, where \mathbf{a} is a nonzero vector, we must first find the unit vector in the direction of \mathbf{a}. The unit vector \mathbf{u} in the direction of \mathbf{a} is \begin{equation*} \mathbf{u}=\frac{\mathbf{a}}{\Vert \mathbf{a}\Vert }=\dfrac{3\mathbf{i}+4 \mathbf{j}}{\sqrt{9+16}}=\frac{3}{5}\mathbf{i}+\frac{4}{5}\mathbf{j} \end{equation*}
The partial derivatives of f f_{x}(x,y)=\sin y\qquad \hbox{and}\qquad f_{y}(x,y)=x\cos y
are continuous throughout the plane, so f is differentiable. Using the unit vector \mathbf{u}=\dfrac{3}{5}\mathbf{i}+\dfrac{4}{5}\mathbf{j=}\cos \theta \mathbf{\mathbf{i}+}\sin \theta \mathbf{{j}}, we find 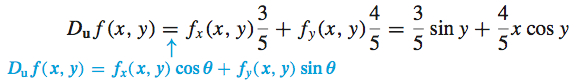
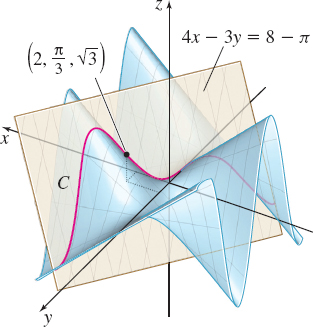
At the point \left( 2,\dfrac{\pi }{3}\right), \begin{equation*} D_{\mathbf{u}}f\!\left( 2,\frac{\pi }{3}\right) =\dfrac{3}{5}\sin \dfrac{\pi }{3}+\dfrac{4}{5}\!\left( 2\cos \dfrac{\pi }{3}\right) =\dfrac{3}{5}\!\left( \frac{\sqrt{3}}{2}\right) +\dfrac{8}{5}\!\left(\dfrac{1}{2}\right)=\frac{3\sqrt{3}+8}{10} \end{equation*}
The slope of the tangent line to the curve C that is the intersection of the surface f( x,y) =x\sin y and the plane perpendicular to the xy-plane that contains the line through the point \left( 2,\dfrac{\pi }{3}, 0\right) in the direction \mathbf{a} is approximately 1.32. See Figure 4.
866
NOW WORK
2 Find the Gradient of a Function of Two VariablesPrinted Page 866
The directional derivative of a differentiable function z=f( x,y) at a point ( x_{0},y_{0}) in the direction of the unit vector \mathbf{u} =\cos \theta \mathbf{i}+\sin \theta \mathbf{j} is given by \begin{equation*} D_{\mathbf{u}}f(x_{0},y_{0})=f_{x}(x_{0},y_{0})\cos \theta +f_{y}(x_{0},y_{0})\sin \theta \end{equation*}
We can express D_{\mathbf{u}}f(x_{0},y_{0}) as the dot product of two vectors as follows: \begin{eqnarray*} D_{\mathbf{u}}f(x_{0},y_{0}) &=&f_{x}(x_{0},y_{0})\cos \theta +f_{y}(x_{0},y_{0})\sin \theta \\ &=&[ f_{x}(x_{0},y_{0})\mathbf{i}+f_{y}(x_{0},y_{0})\mathbf{j}]\,{\bf\cdot}\,[ \cos \theta \mathbf{i}+\sin \theta \mathbf{j}] \\ &=&[ f_{x}(x_{0},y_{0})\mathbf{i}+f_{y}(x_{0},y_{0})\mathbf{j}]\, {\bf\cdot}\, \mathbf{u} \end{eqnarray*}
The vector f_{x}(x_{0},y_{0})\mathbf{i}+f_{y}(x_{0},y_{0})\mathbf{j} is called the gradient of f at ( x_{0},y_{0}).
NEED TO REVIEW?
The dot product is discussed in Section 10.4, pp. 715-716.
DEFINITION Gradient of a Function of Two Variables
Let z=f(x,y) be a differentiable function. The vector {\bf\nabla}\! f(x,y), read “del f,” is called the gradient of f and is defined as \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED]{ {\bf\nabla}\! f(x,y)=f_{x}(x,y)\mathbf{i}+f_{y}(x,y)\mathbf{j}}}
NOTE
“del f” is short for “delta f”; the symbol {\bf\nabla} is an upside down Greek letter delta. In some books, {\bf\nabla}\! f is written as “grad f.” The symbol {\bf\nabla} has no meaning except when it operates on a function z = f (x,y). So, {\bf\nabla} is referred to as an operator, just as \dfrac{d}{dx} is an operator indicating “take the derivative of a function of x.”
The directional derivative D_{\mathbf{u}}f(x,y) of f can be expressed in terms of the gradient of f.
THEOREM The Directional Derivative as a Dot Product
The dot product of the vector {\bf\nabla}\! f(x,y) and the unit vector \mathbf{u}=\cos \theta \mathbf{i}+\sin \theta \mathbf{j} is a scalar that is equal to the directional derivative D_{\mathbf{u}}f(x,y). That is, \begin{equation} \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED]{ {\bf\nabla}\! f(x,y)\,{\bf\cdot}\, \mathbf{u} =D_{\mathbf{u}}f(x,y) }}\tag{3} \end{equation}
Proof
\begin{eqnarray*} {\bf\nabla}\! f(x,y)\,{\bf\cdot}\, \mathbf{u} &=& [f_{x}(x,y) \mathbf{i}+f_{y}(x,y)\mathbf{j}] \,{\bf\cdot}\, [ \cos \theta \mathbf{i} +\sin \theta \mathbf{j}] \\ &=& f_{x}(x,y)\cos \theta +f_{y}(x,y)\sin \theta =D_{\mathbf{u}}f(x,y). \end{eqnarray*}
867
EXAMPLE 3Finding the Gradient of a Function of Two Variables
- (a) Find the gradient of f(x,y)=x^{3}y at the point (2,1).
- (b) Use the gradient to find the directional derivative of f at (2,1) in the direction from (2,1) to (3,5).
Solution (a) The gradient of f at (x,y) is {\bf\nabla}\! f(x,y)=f_{x}(x,y)\mathbf{i}+f_{y}(x,y)\mathbf{j}=3x^{2}y \mathbf{i}+x^{3}\mathbf{j}
The gradient of f at (2,1) is {\bf\nabla}\! f(2,1)=12\mathbf{i}+8\mathbf{j}
(b) The unit vector \mathbf{u} from (2,1) to (3,5) is \begin{equation*} \mathbf{u=}\dfrac{( 3-2) \mathbf{i} +( 5-1) \mathbf{j} }{\sqrt{( 3-2) ^{2}+( 5-1) ^{2}}}=\frac{\mathbf{i}+4 \mathbf{j}}{\sqrt{17}} \end{equation*}
We use formula (3) for the directional derivative to find D_{\mathbf{u} }(2,1). \begin{equation*} D_{\mathbf{u}}(2,1)={\bf\nabla\! }f(2,1)\,{\bf\cdot}\, \mathbf{u}=(12\mathbf{i}+8 \mathbf{j})\,{\bf\cdot}\, \frac{\mathbf{i}+4\mathbf{j}}{\sqrt{17}}=\frac{44}{\sqrt{17} } \end{equation*}
The directional derivative of f at (2,1) in the direction of \mathbf{u} is \dfrac{44}{\sqrt{17}}
NOW WORK
Let’s look more closely at the directional derivative D_{\mathbf{u} }f(x,y). \begin{equation} D_{\mathbf{u}}f(x,y)={\bf\nabla\! }f(x,y)\,{\bf\cdot}\, \mathbf{u} \end{equation}\tag{4}
- If {\bf\nabla}\! f(x_{0},y_{0})=\mathbf{0}, then for any direction \mathbf{u}, D_{\mathbf{u}}f(x_{0},y_{0})={\bf\nabla\! }f(x_{0},y_{0})\,{\bf\cdot}\, \mathbf{u}=\mathbf{0}\,{\bf\cdot}\, \mathbf{u}=0
- If {\bf\nabla}\! f(x_{0},y_{0})\neq \mathbf{0} and \phi, 0\leq \phi \leq \pi, is the angle between the unit vector \mathbf{u} and the gradient {\bf\nabla}\! f(x_{0},y_{0}), then \begin{equation} \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED] {D_{\mathbf{u}}f(x_{0},y_{0})={\bf\nabla\! }f(x_{0},y_{0})\,{\bf\cdot}\, \mathbf{u}=\Vert {\bf\nabla\! }f(x_{0},y_{0})\Vert \Vert \mathbf{u}\Vert \cos \phi =\Vert {\bf\nabla\! }f(x_{0},y_{0})\Vert \cos \phi }} \end{equation}\tag{5}
NEED TO REVIEW?
The angle between two vectors is discussed in Section 10.4, pp. 716-719.
The directional derivative D_{\mathbf{u}}f(x_{0},y_{0}) is largest when \cos \phi =1. This happens if the angle \phi between \mathbf{u} and {\bf\nabla}\! f is 0, or equivalently, if \mathbf{u} and {\bf \nabla}\! f( x_{0},y_{0}) have the same direction. In this case, the maximum value of the directional derivative is \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED]{ \hbox{Maximum value of } D_{\mathbf{u}}f(x_{0},y_{0})=\left\Vert {\bf \nabla\! }f(x_{0},y_{0})\right\Vert }}
Similarly, the minimum value of D_{\mathbf{u}}f(x_{0},y_{0}) occurs when \cos \phi =-1, that is, when \phi =\pi. This happens when \mathbf{u} and {\bf\nabla}\! f are opposite in direction. The minimum value of the directional derivative is \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED]{ \hbox{Minimum value of } D_{\mathbf{u}}f(x_{0},y_{0})=-\left\Vert {\bf \nabla\! }f(x_{0},y_{0})\right\Vert }}
THEOREM Properties of the Gradient
Suppose the function z=f(x,y) is differentiable at (x_{0},y_{0}).
- If {\bf\nabla}\! f(x_{0},y_{0})=\mathbf{0}, then D_{\mathbf{u} }f(x_{0},y_{0})=0 for all directions \mathbf{u}.
- If {\bf\nabla}\! f(x_{0},y_{0})\neq \mathbf{0}, then the directional derivative D_{\mathbf{u}}f( x_{0},y_{0}) of f at (x_{0},y_{0}) is a maximum when \mathbf{u} is in the direction of {\bf\nabla}\! f(x_{0},y_{0}). The maximum value of D_{\mathbf{u}}f(x_{0},y_{0}) is \left\Vert {\bf\nabla\! }f(x_{0},y_{0})\right\Vert.
- If {\bf\nabla}\! f(x_{0},y_{0})\neq \mathbf{0}, then the directional derivative of f at (x_{0},y_{0}) is a minimum when \mathbf{u } is in the direction of -{\bf\nabla}\! f(x_{0},y_{0}). The minimum value of D_{\mathbf{u} }f(x_{0},y_{0}) is -\left\Vert {\bf\nabla\! }f(x_{0},y_{0})\right\Vert.
3 Use Properties of the GradientPrinted Page 868
868
EXAMPLE 4Using Properties of the Gradient
- (a) Find the direction for which the directional derivative of f(x,y)=x^{2}-xy+y^{2} at (1,-2) is a maximum.
- (b) Find the maximum value of the directional derivative.
Solution (a) We begin by finding the gradient of f at (1,-2). \begin{array}{rcl@{\qquad}l} {\bf\nabla\! }f(x,y) &=&(2x-y)\mathbf{i}+(2y-x)\mathbf{j} & \color{#0066A7}{{\bf\nabla}\! f(x,y)=f_{x}(x,y) \mathbf{i}+f_{y}(x,y)\mathbf{j}} \\ {\bf\nabla\! }f(1,-2) &=&4\mathbf{i}-5\mathbf{j} & \color{#0066A7}{{x=1; y=-2}} \end{array}
The direction \mathbf{u} for which D_{\mathbf{u}}f(1,-2) is maximum occurs when {\bf\nabla}\! f and the unit vector \mathbf{u} have the same direction. That is, the directional derivative is a maximum when the direction is \mathbf{u}=\dfrac{4\sqrt{41}}{41}\mathbf{i}-\dfrac{5\sqrt{41}}{ 41}\mathbf{j}.
(b) The maximum value of the directional derivative at (1,-2) equals the magnitude of the gradient, namely \Vert {\bf\nabla}\! f(1,-2)\Vert =\sqrt{16+25}=\sqrt{41}
NOW WORK
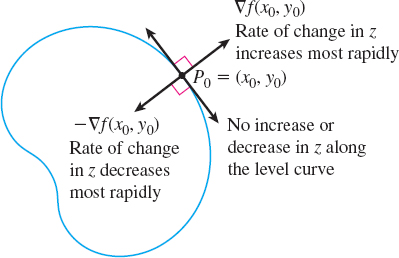
The directional derivative D_{\mathbf{u}}f(x_{0},y_{0}) equals the rate of change of z= f( x,y) at (x_{0},y_{0}) in the direction of \mathbf{u}. When \mathbf{u} has the same direction as {\bf\nabla}\! f(x_{0},y_{0}), then the rate of change of f at (x_{0},y_{0}) is a maximum. It follows that f(x,y) will increase most rapidly in this direction.
THEOREM
Suppose z=f(x,y) is differentiable at (x_{0},y_{0}) and {\bf\nabla}\! f (x_{0},y_{0}) \neq \mathbf{0}.
- The value of z=f(x,y) at (x_{0},y_{0}) increases most rapidly in the direction of {\bf\nabla}\! f(x_{0},y_{0}) and decreases most rapidly in the direction of -{\bf\nabla}\! f(x_{0},y_{0}).
- The value of z= f( x,y) remains the same for directions orthogonal to {\bf\nabla}\! f(x_{0},y_{0}).
The second statement is a consequence of (5). If \phi is the angle between \mathbf{u} and {\bf\nabla}\! f, the rate of change of z in the direction of \mathbf{u} is 0 when \begin{equation*} D_{\mathbf{u}}f(x_{0},y_{0})={\bf\nabla\! }f\,{\bf\cdot}\, \mathbf{u}=\Vert {\bf \nabla\! }f(x_{0},y_{0})\Vert \cos \phi =0 \qquad 0\leq \phi \leq \pi \end{equation*}
If {\bf\nabla}\! f(x_{0},y_{0})\neq \mathbf{0}, then \cos \phi =0, or equivalently, \phi =\dfrac{\pi }{2}. In other words, the rate of change of z is 0 when the direction of \mathbf{u} is orthogonal to {\bf\nabla}\! f(x_{0},y_{0}).
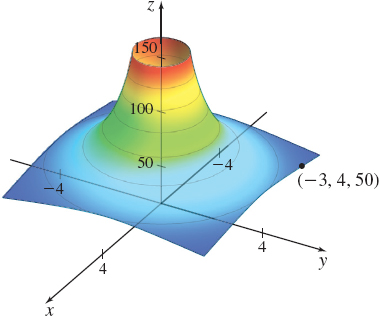
EXAMPLE 5Modeling Temperature Change
A metal plate is placed on the xy-plane in such a way that the temperature T in degrees Celsius at any point P=(x,y) is inversely proportional to the distance of P from (0,0). Suppose the temperature of the plate at the point (-3,4) equals {50^{\circ}{\rm C}}.
- (a) Find T=T( x,y).
- (b) Find the gradient of T at the point ( -3,4).
- (c) In what directions does the temperature increase most rapidly?
- (d) In what directions does the temperature decrease most rapidly?
- (e) In what directions is the rate of change of T at (-3,4) equal to 0?
869
Solution (a) The temperature T at any point (x,y) is inversely proportional to the distance of ( x,y) from the origin (0,0). We can model T=T( x,y) as T(x,y)=\dfrac{k}{\sqrt{x^{2}+y^{2}}}
where k is the constant of proportionality. Since T=50^{\circ}{\rm C} when (x,y)=(-3,4), then k=T\sqrt{x^{2}+y^{2}}=50\sqrt{( -3) ^{2}+4^{2}}=50(5)=250
So, T=T( x,y) =\dfrac{250}{\sqrt{x^{2}+y^{2}}}.
(b) The gradient of T=T( x,y) =\dfrac{250}{\sqrt{ x^{2}+y^{2}}} is {\bf\nabla }T(x,y)=T_{x}(x,y)\mathbf{i}+T_{y}(x,y)\mathbf{j}=-\frac{250x }{(x^{2}+y^{2})^{3/2}}\mathbf{i}-\frac{250y}{(x^{2}+y^{2})^{3/2}}\mathbf{ j}
At ( -3,4), {\bf\nabla }T(-3,4)=-\frac{250 ( -3) }{ [ ( -3) ^{2}+4^{2}] ^{3/2}}\mathbf{i}-\frac{250 ( 4) }{ [ ( -3) ^{2}+4^{2}] ^{3/2}}\mathbf{j}=\frac{750}{125} \mathbf{i}-\frac{1000}{125}\mathbf{j}=6\mathbf{i}-8\mathbf{j}
(c) The temperature increases most rapidly in the direction {\bf\nabla} T(-3,4)=6\mathbf{i}-8\mathbf{j}.
(d) The temperature decreases most rapidly in the direction -{\bf\nabla }T(-3,4)=-6\mathbf{i}+8\mathbf{j}.
(e) The rate of change in T at (-3,4) equals 0 for directions orthogonal to {\bf\nabla} T(-3,4)=6\mathbf{i}-8\mathbf{j}. That is, the rate of change in T is 0 in either of the two directions orthogonal to 6\mathbf{i}-8\mathbf{j}, namely \pm ( 8\mathbf{i}+6 \mathbf{j}).
NEED TO REVIEW?
Level curves are discussed in Section 12.1, pp. 812-814.
Figure 5 shows the graph of the surface T=T( x,y).
NOW WORK
NOTE
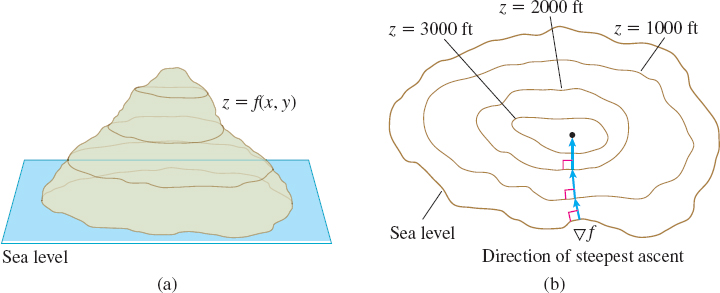
The grade of a mountain is a measure of its steepness. The name gradient given to {\bf\nabla}\! f means the direction of steepest ascent.
Suppose the surface z=f(x,y) represents a mountain whose elevation above sea level is z. See Figure 6(a). The level curves of f shown in Figure 6(b) correspond to contour lines along which the elevation remains fixed. So along the level curves, the value of z does not change. The elevation increases (or decreases) most rapidly in directions perpendicular to the level curves. In other words, the most direct (but steepest) route to the top of the mountain is in the direction of {\bf\nabla}\! f, which is orthogonal to the level curves. The shortest route down the mountain is in the direction of - {\bf\nabla}\!f, which is also perpendicular to the level curves. A stream of water flows this way down the mountain. As water moves from one level curve to another, the gradient changes, giving the water a new direction. See Figure 7.
870
THEOREM The Gradient Is Normal to the Level Curve
Suppose the function z=f(x,y) is differentiable at a point P_{0}=(x_{0},y_{0}). If {\bf\nabla}\! f(x_{0},y_{0})\neq \mathbf{0}, then {\bf\nabla}\! f(x_{0},y_{0}) is normal to the level curve of f at P_{0}.
RECALL
A normal vector to a curve at a point P is defined as a vector with initial point at P and orthogonal (perpendicular) to the tangent line to the curve at P.
Proof
Let f(x,y)=k be the level curve through P_{0}. Suppose this level curve is represented parametrically by x=x(t) and y=y(t), with x_{0}=x(t_{0}) and y_{0}=y(t_{0}). Then \begin{equation*} f( x(t),y(t)) =k \end{equation*}
Differentiating f( x(t),y(t)) with respect to t, we get \begin{equation*} f_{x}( x(t),y(t))\, x′ (t)+f_{y}( x(t),y(t))\, y′ (t)=0 \qquad \color{#0066A7}{\hbox{Use Chain Rule I.}} \end{equation*}
or, equivalently, \begin{equation*} {\bf\nabla\! }f(x,y)\,{\bf\cdot}\, \lbrack x′ (t)\mathbf{i}+y′ (t) \mathbf{j}]=0 \end{equation*}
Since x′ (t) \mathbf{i}+y′ (t) \mathbf{j} is tangent to the level curve, the vector {\bf\nabla\! }f( x,y) is normal to the level curve. In particular, when t=t_{0}, {\bf\nabla}\! f(x_{0},y_{0}) is normal to the level curve of f at (x_{0},y_{0}).
EXAMPLE 6Using Properties of the Gradient
For the function f(x,y)=\sqrt{x^{2}+y^{2}}, graph the level curve containing the point (3,4) and graph the gradient {\bf\nabla\! }f(x,y) at this point.
Solution See Figure 8(a). The graph of the equation z=\sqrt{x^{2}+y^{2}} is the upper half of a circular cone whose traces are circles. So, the level curves are concentric circles centered at ( 0,0). Because f(3,4)=\sqrt{9+16}=5, the level curve through (3,4) is the circle x^{2}+y^{2}=25. Since \begin{equation*} {\bf\nabla}\! f(x,y)=\frac{x}{\sqrt{x^{2}+y^{2}}}\mathbf{i}+\frac{y}{\sqrt{ x^{2}+y^{2}}}\mathbf{j} \end{equation*}
the gradient at (3,4) is \begin{equation*} {\bf\nabla}\! f(3,4)=\frac{3}{5}\mathbf{i}+\frac{4}{5}\mathbf{j} \end{equation*}
This vector is orthogonal to the level curve x^{2}+y^{2}=25, as shown in Figure 8(b).
NOW WORK
4 Find the Directional Derivative and Gradient of a Function of Three VariablesPrinted Page 871
871
The concepts of directional derivative and gradient can be extended to a function w=f(x,y,z) of three variables.
DEFINITION Directional Derivative of a Function of Three Variables
The directional derivative D_{\mathbf{u} }f(x_{0},y_{0},z_{0}) of a function w=f(x,y,z) at (x_{0},y_{0},z_{0}) in the direction of a unit vector \mathbf{u=} \cos \alpha \mathbf{i} +\cos \beta \mathbf{j}+\cos \gamma \mathbf{k} is given by \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED]{ D_{\mathbf{u}}f(x_{0},y_{0},z_{0})=\lim\limits_{t\rightarrow 0} \dfrac{f(x_{0}+t\cos \alpha ,y_{0}+t\cos \beta ,z_{0}+t\cos \gamma )-f(x_{0},y_{0},z_{0})}{t} }}
provided the limit exists.
If the function w= f(x,y,z) is differentiable, then the directional derivative of f in the direction of \mathbf{u}=\cos \alpha \mathbf{i} +\cos \beta \mathbf{j}+\cos \gamma \mathbf{k} equals \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED]{ D_{\mathbf{u}}f(x_{0},y_{0},z_{0})=f_{x}(x_{0},y_{0},z_{0})\cos \alpha +f_{y}(x_{0},y_{0},z_{0})\cos \beta +f_{z}(x_{0},y_{0},z_{0})\cos \gamma }}
As with functions of two variables, the directional derivative D_{\mathbf{u} } f(x_{0}, y_{0}, z_{0}) equals the rate of change of f at (x_{0}, y_{0}, z_{0}) in the direction of \mathbf{u}.
DEFINITION Gradient of a Function of Three Variables
Let w = f(x,y,z) be a differentiable function. Then the gradient of f at (x_{0},y_{0},z_{0}) is the vector \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED]{ {\bf\nabla}\! f(x_{0},y_{0},z_{0})=f_{x}(x_{0},y_{0},z_{0})\mathbf{i} +f_{y}(x_{0},y_{0},z_{0})\mathbf{j}+f_{z}(x_{0},y_{0},z_{0})\mathbf{k} }}
Then, as for functions of two variables, the directional derivative of f at \left( x_{0},y_{0},z_{0}\right) in the direction of \mathbf{u} can be found using the gradient as follows: \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED]{ D_{\mathbf{u}}f(x_{0},y_{0},z_{0})= \bf\nabla\! f(x_{0},y_{0},z_{0})\,{\bf\cdot}\, \mathbf{u}=\left\Vert {\bf\nabla\! } f(x_{0},y_{0},z_{0})\right\Vert \cos \phi }}
where \phi is the angle between {\bf\nabla}\! f(x_{0},y_{0},z_{0}) and \mathbf{u}.
As with functions of two variables, the value of f increases most rapidly in the direction of the gradient {\bf\nabla\! }f(x_{0},y_{0},z_{0}), and decreases most rapidly in the direction of -{\bf\nabla\! } f(x_{0},y_{0},z_{0}).
For example, suppose T=T(x,y,z) is the temperature of a homogeneous object at the point (x,y,z). At the point (x_{0},y_{0},z_{0}) on the object, heat will flow in the direction of greatest decrease in temperature, namely in the direction of -{\bf\nabla }T(x_{0},y_{0},z_{0}). This direction of greatest heat transfer is normal to the level surface through (x_{0},y_{0},z_{0}).
THEOREM The Gradient Is Normal to the Level Surface
Suppose the function w = f(x, y, z) is differentiable at a point P_{0}=(x_{0}, y_{0}, z_{0}). If {\bf\nabla\! }f(x_{0}, y_{0}, z_{0})\neq \mathbf{0}, the gradient {\bf\nabla\! }f(x_{0}, y_{0}, z_{0}) is normal to the level surface of f through P_{0}.
You are asked to prove this in Problem 76.