Functions of Several Variables

12.1 Functions of Two or More Variables and Their Graphs
Printed Page 810

810

OBJECTIVES

When you finish this section, you should be able to:

Work with functions of two or three variables (p. 810)
Graph functions of two variables (p. 812)
Graph level curves (p. 812)
Describe level surfaces (p. 815)

1 Work with Functions of Two or Three Variables
Printed Page 810

Many applications of the physical sciences, biology, the social sciences, business and economics, and even sports require functions of two or more variables. For example, the monthly cost of using a netbook depends on the megabytes of data used domestically, the number of kilobytes of data sent to or received from Canada, and the number of kilobytes of data used outside the United States and Canada. The cost is a function of three variables. For another example, the volume $V$ $=\pi R^{2}h$ of water stored in a cylindrical tank depends on both the height $h$ of the water and the radius $R$ of the tank. The volume $V$ is a function of two variables, $R$ and $h$ . In function notation, $\begin{equation*} V=f(R,h)=\pi R^{2}h \end{equation*}$

So, if $R=10$ centimeters (cm) and $h=3$ cm, then the volume of water in the tank is $V=f(10,3)=\pi (10^{2})(3)=300\pi$ cubic centimeters (cm $^3$ ).

DEFINITION Function of Two Variables

Let $D$ be a nonempty subset of the $xy$ -plane. A function $f$ of two variables $x$ and $y$ is a rule that associates with each point $(x,y)$ of $D$ a unique real number $z=f(x,y).$

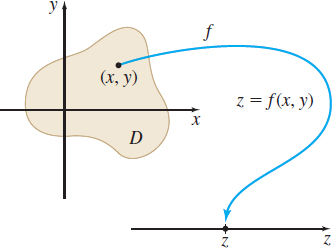
The function $z=f(x,y)$ has two independent variables $x$ and $y,$ and one dependent variable $z.$ The domain $D$ of the function $f$ is the set of points in the $xy$ -plane for which the function is defined. The range of $f$ is the set of real numbers $z= f(x,y),$ where $(x,y)$ is in $D$ . Figure 1 illustrates how the point $(x,y)$ is mapped to the number $z=f(x,y)$ .

Figure 1

$D$ is the domain of

$f$ ;

$z=f(x,y)$ is in the range of

$f.$

EXAMPLE 1Evaluating a Function of Two Variables

Let $f(x,y)=\sqrt{x}+x\sqrt{y}$ . Find:

$f(1,4)$
$\!f(a^{2},9b^{2})$ , $a>0$ , $b>0$
$f(x+\Delta x, y)$
$f(x,y+\Delta y)$

(a) $f(1,4)=\sqrt{1}+1\sqrt{4}=1+2=3\qquad\hspace{5.2pt}$ $\color{#0066A7}{x=1; y=4}$ .

(b) $f(a^{2},9b^{2})=\sqrt{a^{2}}+a^{2} \sqrt{9b^{2}}=a+3a^{2}b\quad \color{#0066A7}{x=a^{2}; y=9b^{2}; a>0; b>0.}$

(c) $f(x+\Delta x, y)=\sqrt{x+\Delta x}+( x+\Delta x) \sqrt{y}$

(d) $f(x,y+\Delta y)=\sqrt{x}+x\sqrt{y+\Delta y}$

NOW WORK

Problem 7.

DEFINITION Function of Three Variables

Let $D$ be a nonempty set of points in space. A function $f$ of three variables $x, y$ , and $z$ is a rule that associates with each point $(x,y,z)$ of $D$ a unique real number $w=f(x, y, z)$ .

811

Figure 2

$D$ is the domain of

$f$ ;

$w$ is the value of

$f (x, y, z$ ).

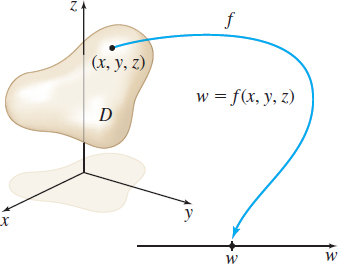
The function $w=f(x,y,z)$ has three independent variables $x,$ $y,$ and $z$ and one dependent variable $w.$ The domain $D$ of the function $f$ is the set of points in space for which the function is defined, and the range of $f$ is the set of real numbers $w= f(x,y, z)$ for points $(x,y,z)$ in $D$ . See Figure 2.

Functions of $n$ variables, where $n$ is a positive integer, are defined similarly. A function $f$ of $n$ variables $x_{1}, x_{2}, \ldots , x_{n}$ is a rule that associates a unique real number $z=f(x_{1}, x_{2}, \ldots , x_{n})$ with each point $(x_{1}, x_{2}, \ldots , x_{n})$ in a nonempty subset $D$ of $n$ -dimensional space. Here, $z$ is the dependent variable and $x_{1}, x_{2}, \ldots , x_{n}$ are the $n$ independent variables.

Collectively, functions of two or more variables are referred to as functions of several variables. As with functions of a single variable, a function of several variables is usually given by a formula, and unless the domain is specified, the domain is the largest set of points for which the dependent variable is a real number.

Functions of several variables are expressed explicitly when they are in the form $z=f(x,y) \qquad w=g(x,y,z) \qquad z=h(x_{1}, x_{2}, \cdots , x_{n})$

or implicitly when they are in the form $F(x,y,z) =0 \qquad G( x,y,z,w) =0 \qquad H( x_{1}, x_{2}, \cdots , x_{n},z) =0$

EXAMPLE 2Finding the Domain of a Function of Two Variables

Find the domain of each of the following functions. Then graph the domain.

$z=f(x, y)=\sqrt{16-x^{2}-y^{2}}$
$z= f(x,y)=\ln (y^{2}-4x)$

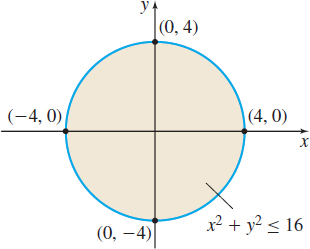
(a) Since the expression under the radical must be nonnegative, the domain of $f$ consists of all points in the plane for which $\begin{eqnarray*} 16-x^{2}-y^{2} &\geq &0 \\[4pt] x^{2}+y^{2} &\leq &16 \end{eqnarray*}$

The domain is all the points inside and on the circle $x^{2}+y^{2}=16$ . The shaded portion of Figure 3 illustrates the domain.

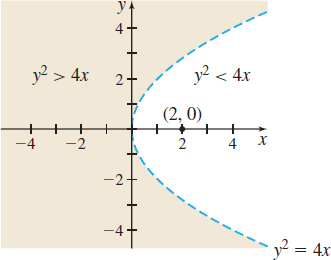
(b) Since the logarithmic function is defined for only positive numbers, the domain of $f$ is the set of points $(x,y)$ for which $y^{2}-4x>0$ or $y^{2}>4x$ . To graph the domain, we start with the parabola $y^{2}=4x,$ and use a dashed curve to indicate that the parabola is not part of the domain. The parabola $y^{2}=4x$ divides the plane into two sets of points: those for which $y^{2}<4x$ and those for which $y^{2}>4x$ . To find which points are in the domain, choose any point not on the parabola $y^{2}=4x$ and determine whether it satisfies the inequality. For example, the point $(2,0)$ is not in the domain, since $0^{2}<(4)(2)$ . The set of points for which $y^{2}>4x$ , the domain of $f$ , is shaded in Figure 4.

Figure 3 The domain of

$f(x, y)=\sqrt{16-x^2-y^2}$ .

Figure 4 The domain of

$f (x,y) = \ln (y^{2} -4x )$ .

NOW WORK

Problems 13 and 17.

812

Figure 5

$f(x, y, z)=\sqrt{x^2+y^2+z^2-1}$

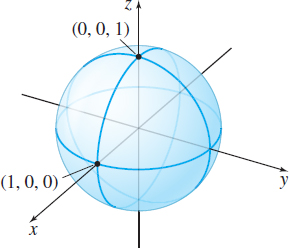
EXAMPLE 3Finding the Domain of a Function of Three Variables

Find the domain of the function $w=f(x,y,z)=\sqrt{x^{2}+y^{2}+z^{2}-1}$ and graph the domain.

Since the expression under the radical must be nonnegative, the domain of $f$ consists of all points for which $x^{2}+y^{2}+z^{2}-1\geq 0.$ The domain is the set of all points on and outside of the unit sphere $x^{2}+y^{2}+z^{2}=1$ ; that is, the set $\{ (x,y,z) \,|\,x^{2}+y^{2}+z^{2}\geq 1\}$ . See Figure 5.

NOW WORK

Problem 25.

2 Graph Functions of Two Variables
Printed Page 812

The graph of a function $z=f(x,y)$ of two variables is called a surface and consists of all points $(x,y,z)$ for which $z=f(x,y),$ and $(x,y)$ is in the domain of $f$ . We use the graphing techniques introduced in Chapter 10 to graph functions of two variables.

EXAMPLE 4Graphing a Function of Two Variables

Graph each function:

$z=f(x,y)=1-x-y$
$z=f(x,y)=x^{2}+4y^{2}$
$z=f(x,y)=\sqrt{x^{2}+y^{2}}$

NEED TO REVIEW?

Planes in space are discussed in Section 10.6, pp. 737-740.

(a) The graph of the equation $z=1-x-y$ , or $x+y+z=1$ , is a plane. The intercepts are the points $(1,0,0),$ $(0,1,0)$ , and $(0,0,1)$ . See Figure 6.

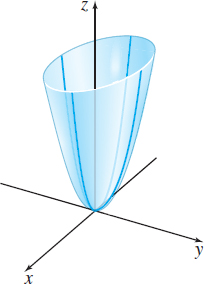
(b) The graph of the equation $z=x^{2}+4y^{2}$ is an elliptic paraboloid whose vertex is at the origin. See Figure 7.

NEED TO REVIEW?

Quadric surfaces are discussed in Section 10.7, pp. 744-751.

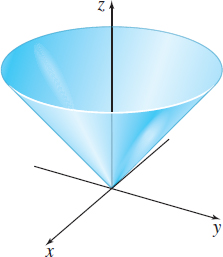
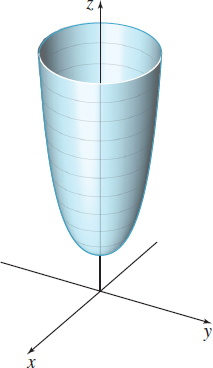
(c) The equation $z=f(x,y) =\sqrt{x^{2}+y^{2}}$ is equivalent to $z^{2}=x^{2}+y^{2}$ , where $z\geq 0$ . The graph of the equation is part of a circular cone whose vertex is at the origin. Since $z\geq 0,$ the graph of $f$ is the upper nappe of the cone. See Figure 8.

Figure 6

$z=f (x,y) =1-x-y$

Figure 7

$z=f(x, y)=x^{2} + 4y^{2}$

Figure 8

$z=f (x,y) = \sqrt{x^2 +y^2}$

NOW WORK

Problems 29, 33, and 37.

3 Graph Level Curves
Printed Page 812

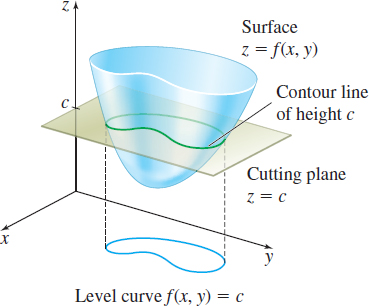
The graph of a function $f$ of two variables is usually difficult to draw by hand. In practice, such as in topography, the surface $z=f(x,y)$ is conveyed by drawing properly labeled curves for fixed values of $z$ . These curves are called contour lines and each contour line corresponds to the intersection of the surface $z=f(x,y)$ and a plane $z=c,$ where $c$ is a constant.

813

For example, suppose the surface is a mountain whose height is measured in meters, and $z=0$ represents sea level. Then by walking along the contour line $z=500,$ we would be walking on a level path 500 m above sea level.

NOTE

A contour line is equivalent to a trace used to describe a quadric surface in Chapter 10. Recall that a trace is the intersection of a surface with a coordinate plane or a plane parallel to a coordinate plane.

When a contour line is projected onto the $xy$ -plane, the resulting graph is called a level curve. See Figure 9.

Figure 9 Level curve of

$z=f(x,y)$ at

$z=c$ .

In a topographical map, a series of level curves are drawn, each representing a contour line of height (or depth) $c.$ For example, to represent a hilly terrain, a topographer draws level curves corresponding to contour lines for various heights measured at equal intervals, say, every 100 m. When the level curves are close to each other, the terrain is steep; when they are further apart, the terrain is flatter. See Figure 10.

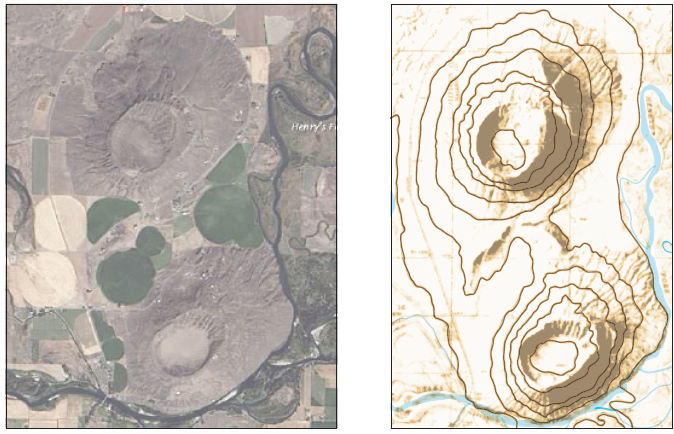
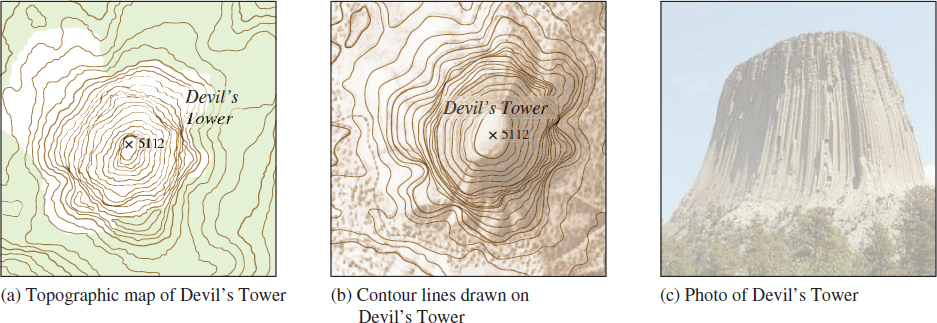
Figure 10 Menan Buttes, ID. Contour intervals are shown for each 100-ft change in altitude. The north crater is about 100 ft deep, and the south crater is about 150 ft deep.

So by reversing the process, we can visualize a surface by mentally raising each level curve to its corresponding height $z$ and viewing the resulting contour lines. Figure 11 shows this process. Figure 11(a) is a U.S. geological survey topographic map of Devil’s Tower, a monolith in Wyoming. Observe how the level curves are close together, indicating that the surface is steep on all sides. Figure 11(b) shows the contour lines drawn on the monolith. Figure 11(c) is a photograph of Devil’s Tower.

Figure 11

Level curves are used by meteorologists to indicate points at which barometric pressure is fixed (isobars), to illustrate places at which wind speed remains constant (isolines), and to show temperature bands (isotherms).

IN WORDS

The prefix iso- is Greek meaning “same.”

814

EXAMPLE 5Graphing Level Curves

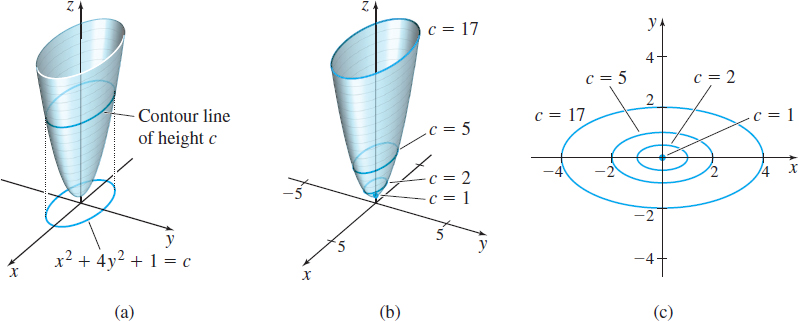
Graph the level curves of the function $z=f(x, y)=x^{2}+4y^{2}+1$ for $c = 1,2,5$ , and $17.$

Here, we recognize the graph of $f$ to be an elliptic paraboloid, as shown in Figure 12. Since $z\geq 1,$ the level curves of $f$ consist of the graphs of $x^{2}+4y^{2}=c-1,$ $c\geq 1.$ Figure 13(a) shows the elliptic paraboloid and a level curve $x^{2}+4y^{2}+1=c\qquad c>1$

Figure 12

Figure 13(b) shows the elliptic paraboloid $\ z=x^{2}+4y^{2}+1$ with several contour lines marked. The level curves for $c=1$ [the point $(0,0)$ ], $c=2, c=5$ , and $c=17$ are then graphed in Figure 13(c). Notice that the level curves are concentric ellipses. You should be able to see how the elliptic paraboloid evolves from the collection of its level curves.

Figure 13

NOW WORK

Problem 39.

EXAMPLE 6Graphing Level Curves

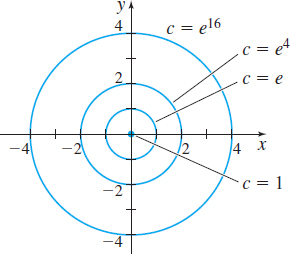
Graph the level curves of the function $z=f(x,y)=e^{x^{2}+y^{2}}$ for $c=1, e, e^{4},$ and $e^{16}$ .

Because $x^{2}+y^{2}\geq 0,$ it follows that $z\geq e^{0}=1$ . The level curves satisfy the equation $e^{x^{2}+y^{2}}=c$ or $x^{2}+y^{2}=\ln c,$ where $c\geq 1$ . For $c=1,$ the level curve is the point $(0,0)$ . If $c>1,$ the level curves are concentric circles. Figure 14 illustrates several level curves of $f$ . A graph of the surface $z=e^{x^{2}+y^{2}}$ is given in Figure 15. Do you see how the graph evolved from the collection of its level curves?

Figure 14 Level curves of

$z=e^{x^2+y^2}$ .

Figure 15 The surface

$z=e^{x^2+y^2}$ .

NOW WORK

Problem 43.

4 Describe Level Surfaces
Printed Page 815

815

The graph of a function $w=f(x,y,z)$ of three variables consists of all points $(x,y,z,w)$ for which $w=f(x,y,z)$ and $(x,y,z)$ is in the domain of $f$ . We cannot draw the graph of a function of three variables because it requires four dimensions. But we can visualize the graph by examining its level surfaces, that is, the surfaces obtained by letting $w$ equal a constant.

EXAMPLE 7Describing Level Surfaces

Figure 16 Level surfaces

$x^{2} + y^{2} + z^{2} =c$ .

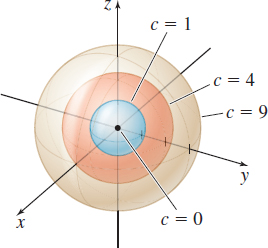
Describe the level surfaces of the function $w=f(x,y,z)=x^{2}+y^{2}+z^{2}$ .

Since $w\geq 0$ , the level surfaces are the graphs of $\begin{equation*} x^{2}+y^{2}+z^{2}=c\qquad c\geq 0 \end{equation*}$

These are concentric spheres if $c>0$ and the origin if $c=0.$ See Figure 16.

NOW WORK

Problem 47.

EXAMPLE 8Describing Level Surfaces

Describe the level surfaces of the function $w=f(x,y,z)=2x+3y+z$ .

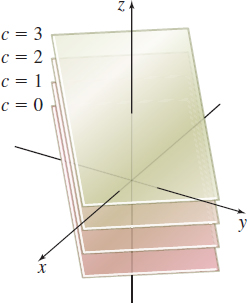
The level surfaces are the graphs of $2x+3y+z=c$

Figure 17

This is a collection of parallel planes, each plane having the vector $\mathbf{N}=2\mathbf{i}+3\mathbf{j}+\mathbf{k}$ as normal. See Figure 17.

NOW WORK

Problem 49.

●

◌

▣

12.1 Functions of Two or More Variables and Their GraphsPrinted Page 810

OBJECTIVES

1 Work with Functions of Two or Three VariablesPrinted Page 810

DEFINITION Function of Two Variables

EXAMPLE 1Evaluating a Function of Two Variables

NOW WORK

DEFINITION Function of Three Variables

EXAMPLE 2Finding the Domain of a Function of Two Variables

NOW WORK

EXAMPLE 3Finding the Domain of a Function of Three Variables

NOW WORK

2 Graph Functions of Two VariablesPrinted Page 812

EXAMPLE 4Graphing a Function of Two Variables

NEED TO REVIEW?

NEED TO REVIEW?

NOW WORK

3 Graph Level CurvesPrinted Page 812

NOTE

IN WORDS

EXAMPLE 5Graphing Level Curves

NOW WORK

EXAMPLE 6Graphing Level Curves

NOW WORK

4 Describe Level SurfacesPrinted Page 815

EXAMPLE 7Describing Level Surfaces

NOW WORK

EXAMPLE 8Describing Level Surfaces

NOW WORK

12.1 Functions of Two or More Variables and Their Graphs
Printed Page 810

1 Work with Functions of Two or Three Variables
Printed Page 810

2 Graph Functions of Two Variables
Printed Page 812

3 Graph Level Curves
Printed Page 812

4 Describe Level Surfaces
Printed Page 815