12.4 Differentiability and the DifferentialPrinted Page 840
For a function y=f(x) of a single variable, we said that when f has a derivative, then f is differentiable. We also defined the differential of y in terms of its derivative as dy=f′(x) dx, where dx=Δx. For functions of more than one variable, the situation is a little more involved. We begin by defining what it means for a function z=f(x,y) to be differentiable, which involves the change Δz in z. Then under suitable conditions on z , we will define dz, the differential of z.
1 Find the Change in z=f(x,y)Printed Page 841
841
If y=f(x) is a function of one variable, then the change Δy in y from x0 to x0+Δx is Δy=f(x0+Δx)−f(x0)
There is a similar definition for a function z=f(x,y) of two variables.
DEFINITION Change in z=f(x,y)
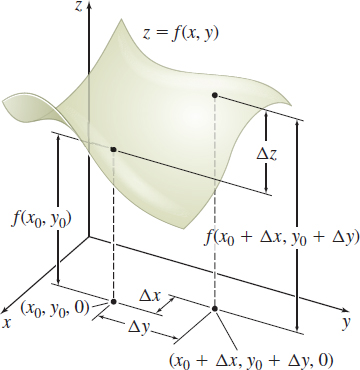
Let z=f(x,y) be a function of two variables with domain D. Let (x0,y0) be an interior point of D, and let Δx and Δy represent changes in x and in y, respectively. If Δx and Δy are chosen so that the point (x0+Δx,y0+Δy) is also in D, then the change in z, denoted by Δz, is defined as \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \Delta z=f(x_{0}+\Delta x, y_{0}+\Delta y)-f(x_{0}, y_{0})}}
See Figure 36.
EXAMPLE 1Finding the Change in z
- (a) Find the change \Delta z in z=f(x,y)=x^{2}y-1 from (x_{0},y_{0}) to (x_{0}+\Delta x, y_{0}+\Delta y).
- (b) Use the answer to calculate the change in z from (1,2) to (1.1,1.9).
Solution (a) \begin{eqnarray*} \Delta z&=&f(x_{0}+\Delta x, y_{0}+\Delta\;y)-f(x_{0},y_{0})\nonumber\\ &=& [ (x_{0}+\Delta x)^{2}(y_{0}+\Delta y)-1]-[ x_{0}^{2}\,y_{0}-1] \end{eqnarray*}
(b) Let (x_{0},y_{0}) =(1,2) and (x_{0}+\Delta x,y_{0}+\Delta y) =( 1.1,1.9). Then \Delta z=[ ( 1.1) ^{2}( 1.9) -1] -[(1) ^{2}( 2) -1] =0.299
NOW WORK
2 Show That a Function of Two Variables Is DifferentiablePrinted Page 841
NEED TO REVIEW?
The differentials dx and dy of a function y=f (x) of one variable are discussed in Section 3.4, pp. 230-232.
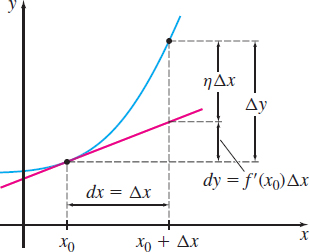
Before defining the differentiability of a function of two variables, let’s reexamine the differential dy of a function y=f(x) of a single variable. For a differentiable function y=f(x) of one variable, the differentials dx=\Delta x and dy=f' (x)\ dx=f' (x) \Delta x can be used to approximate \Delta y=f(x_{0}+\Delta x)-f(x_{0}). That is, dy\approx \Delta y=f(x_{0}+\Delta x)-f(x_{0})
provided \Delta x is close to 0.
NOTE
\eta is the Greek letter eta.
If the error in using dy to approximate \Delta y is \eta \Delta x, then \begin{eqnarray*} \Delta y-dy &=&\eta \Delta x \nonumber \\[4pt] \Delta y &=&f' (x_{0})\Delta x+\eta \Delta x \qquad\quad {\color{#0066A7}{\hbox{\(dy=f' (x_{0}) \Delta x\)}}} \tag{1} \end{eqnarray*}
where \eta is a function of \Delta x for which \lim\limits_{\Delta x\rightarrow 0}\eta =0.
Figure 37 gives a geometric interpretation of equation (1). From Figure 37, we can see that \eta \Delta x\rightarrow 0 as \Delta x\rightarrow 0. But Figure 37 does not show something else suggested by equation (1), namely that \eta \rightarrow 0 as \Delta x\rightarrow 0. Do you see why? From (1), \dfrac{\Delta y}{\Delta x}=f' \left( x_{0}\right) +\eta . Since f is differentiable, \lim\limits_{\Delta x\rightarrow 0}\dfrac{\Delta y}{\Delta x}=f' (x_{0}). This means \lim\limits_{\Delta x\rightarrow 0}\eta must be 0.
The discussion above provides background for the definition of differentiability of a function of two variables.
842
DEFINITION Differentiability of z=f(x,y) at (x_{0},y_{0})
Let z=f(x,y) be a function of two variables whose domain is D. Let (x_{0},y_{0}) be an interior point of D and let \Delta x and \Delta y be chosen so that the point (x_{0}+\Delta x, y_{0}+\Delta y) is also in D. If the change \Delta z from (x_{0},y_{0}) to (x_{0}+\Delta x,y_{0}+\Delta y) can be expressed in the form \begin{equation*}{\bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \Delta z=f_{x}(x_{0},y_{0})\Delta x+f_{y}(x_{0},y_{0})\Delta y+\eta _{1}\Delta x+\eta _{2}\Delta y }}} \tag{2} \end{equation*}
where both \eta _{1} and \eta _{2} are functions of \Delta x and \Delta y for which \begin{equation*} \lim\limits_{(\Delta x, \Delta y)\rightarrow (0,\, 0)}\eta _{1}=0\qquad \hbox{and}\qquad \lim\limits_{(\Delta x, \Delta y)\rightarrow (0,\, 0)}\eta _{2}=0 \tag{3} \end{equation*}
then z=f(x,y) is said to be differentiable at the point (x_{0},y_{0}).
If the domain D of a function z=f(x,y) is an open set and if z=f(x,y) is differentiable at every point of D, then we say f is differentiable on D.
EXAMPLE 2Showing That a Function of Two Variables Is Differentiable
Show that z=f(x, y)=x^{2}y-1 is differentiable.
Solution The domain of f is the xy-plane and the partial derivatives of f are f_{x}(x,y) =2xy\qquad \hbox{and}\qquad f_{y}(x,y) =x^{2}
We find the change \Delta z in z and express it in the form of (2). \begin{eqnarray*} \Delta z &=& [ (x+\Delta x)^{2}(y+\Delta y)-1 ] - [ x^{2}y-1 ]\\ &=& [ x^{2}+2x\Delta x+ ( \Delta x ) ^{2} ] ( y+\Delta y ) - x^{2}y \\ &=&x^{2}\Delta y+2xy\Delta x+2x\Delta x\Delta y+y(\Delta x)^{2}+(\Delta x)^{2}\Delta y \\ &=&\underset{\color{#0066A7}{\hbox{\(f_{x}(x,y)\)}}}{\underbrace{ ( 2xy ) }}\Delta x+\! \underset{\color{#0066A7}{\hbox{\(f_{y}(x,y)\)}}}{\underbrace{ ( x^{2} ) }} \Delta y+\,\underset{\color{#0066A7}{\hbox{\(\eta _{1}\)}}}{\underbrace{ [ y\Delta x ] }}\Delta x+\,\underset{\color{#0066A7}{\hbox{\(\eta _{2}\)}}}{\underbrace{ [ 2x\Delta x+(\Delta x)^{2} ] }}\Delta y\\ &=&f_{x}(x,y) \Delta x+f_{y}(x,y) \Delta y+\eta _{1}\Delta x+\eta _{2}\Delta y \end{eqnarray*}
Equation (2) is satisfied. It remains to show that equation (3) is satisfied. \lim_{(\Delta x, \Delta y)\rightarrow (0, 0)}\eta _{1}=\lim_{\Delta x\rightarrow 0}( y\Delta x) =0\quad\!\! \hbox{and}\!\!\quad \lim_{( \Delta x,\Delta y) \rightarrow (0,0) }\eta _{2}=\lim_{\Delta x\rightarrow 0}[ 2x\Delta x+(\Delta x)^{2}] =0
So, z=f(x,y) is differentiable on its domain.
NOTE
There are other ways to choose \eta _{1} and \eta _{2} so that equations (2) and (3) are satisfied.
NOW WORK
Although not every function z=f(x,y) is differentiable, there are conditions on a function z=f(x,y) that will guarantee it is differentiable.
THEOREM Continuous Partial Derivatives Are Sufficient for Differentiability
Let z=f(x,y) be a function of two variables whose domain is D. Let (x_{0},y_{0}) be an interior point of D. If the partial derivatives f_{x} and f_{y} exist at each point of some disk centered at (x_{0},y_{0}), and if f_{x} and f_{y} are each continuous at (x_{0},y_{0}), then f is differentiable at (x_{0},y_{0}).
The proof of this result is given in Appendix B.
Now we are ready to define the differential dz of a function z=f(x,y).
843
DEFINITION Differential dz of z=f(x,y)
Let z=f(x,y) be a function of two variables whose domain is D. Let (x_{0},y_{0}) be an interior point of D and let \Delta x and \Delta y be chosen so that the point (x_{0}+\Delta x,y_{0}+\Delta y) is also in D. If f is differentiable at the point (x_{0},y_{0}), then the differentials dx and dy are defined as \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ dx=\Delta x\qquad \hbox{and}\qquad dy=\Delta y }}
The differential dz, also called the total differential of z=f(x,y) at (x_{0},y_{0}), is defined as \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ dz=f_{x}(x_{0},y_{0})\,dx+f_{y}(x_{0},y_{0})\,dy }}
EXAMPLE 3Finding the Differential dz of z=f(x,y)
Find the differential dz of each function:
- (a) f(x,y) =e^{x}\cos\;y
- (b) f(x,y) =\dfrac{\ln\;x}{y}
Solution (a) f is defined everywhere in the xy-plane. The partial derivatives of f are \begin{equation*} f_{x}(x,y) =e^{x}\cos\;y\qquad f_{y}(x,y) =-e^{x}\;\sin\;y \end{equation*}
Since f_{x} and f_{y} are continuous everywhere in the xy-plane, the function z=f(x,y) is differentiable. The differential dz is dz=e^{x}\cos\;y\,dx-e^{x}\sin\;y\,dy
(b) The domain of f is \left\{(x,y) \,|\,x>0,\,y\neq 0\right\} . The partial derivatives of f are f_{x}(x,y) =\dfrac{1}{xy}\qquad f_{y}(x,y) =-\dfrac{\ln\;x}{y^{2}}
Since both partial derivatives exist and are continuous at every point (x_{0},y_{0}) in the domain of f, the function z=f(x,y) is differentiable at every point (x_{0},y_{0}) in its domain. The differential dz is dz=\dfrac{1}{xy}\, dx-\dfrac{\ln\;x}{y^{2}}\,dy
NOW WORK
If z=f(x,y) is a differentiable function, then \Delta z can be expressed in terms of the differential dz. 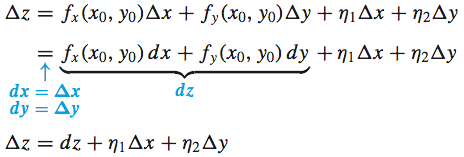
where \lim\limits_{(\Delta x, \Delta y)\rightarrow (0, 0)}\eta _{1}=0 and \lim\limits_{(\Delta x, \Delta y)\rightarrow (0, 0)}\eta _{2}=0.
When the differentials dx=\Delta x and dy=\Delta y are close to 0, then \eta _{1} and \eta _{2} are also close to 0, and the differential dz is approximately equal to \Delta z. That is, \begin{equation*}{ \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \Delta z\approx dz=f_{x}(x_{0},y_{0})\,dx+f_{y}(x_{0},y_{0})\,dy }}} \tag{4} \end{equation*}
The differential dz is usually easier to calculate than \Delta z, making dz a useful approximation to \Delta z. The error introduced in using dz to approximate \Delta z equals the expression \eta _{1}\Delta x+\eta _{2}\Delta y.
3 Use the Differential dz to Approximate a Change in zPrinted Page 844
844
EXAMPLE 4Using the Differential dz to Approximate the Change in z
For the function z=f(x, y)=x^{2}y-1, use the differential dz to approximate the change in z from (1,2) to (1.1,1.9).
Solution Example 2 shows f is differentiable and f_{x}(x,y) =2xy and f_{y}(x,y) =x^{2}.
Let ( x_{0},y_{0}) =( 1,2) and ( x_{0}+\Delta x,y_{0}+\Delta y) =( 1.1,1.9) . Then dx=\Delta x=1.1-1=0.1, \hbox{ and } dy=\Delta y=1.9-2= -0.1.
Using (4), an approximation to the change in z is \Delta z\approx dz=f_{x}(1,2)\,dx+f_{y}(1,2)\,dy=2(1) (2) ( 0.1) +(1) ( -0.1) =0.4-0.1=0.3
The actual change in z was computed in Example 1 to be 0.299, so using the differential dz to approximate \Delta z results in an error of 0.001.
NOW WORK
EXAMPLE 5Using the Differential in Astronomy
The luminosity L (total power output in watts, W) of a star is given by the formula L=L( R,T) =4\pi R^{2}\sigma T^{4}
where R is the radius of the star (in meters), T is its effective surface temperature (in kelvin, K), and \sigma is the Stefan–Boltzmann constant. For the sun, L_{s}=(3.90\times\;10^{26}) \rm{W}, R_{s}=(6.94\times\;10^{8})\;\rm{m} , and T_{s}=4800\;\rm{K}. Suppose in a billion years, the changes in the Sun will be \Delta R_{s}=(0.08\;\times\;10^{8})\;\rm{m} and \Delta T_{s}=100\;\rm{K}. What will be the resulting percent increase in luminosity?
Solution We begin with L=4\pi\;R^{2}\sigma\;T^{4}. Then dL=4\pi \sigma (2R) T^{4}dR+4\pi \sigma R^{2}( 4T^{3}) dT=8\pi \sigma RT^{3}( T dR+2R\ dT)
The relative error in luminosity is \begin{eqnarray*} \frac{\Delta L}{L}&\approx& \frac{dL}{L}=\dfrac{8\pi \sigma RT^{3}}{4\pi R^{2}\sigma T^{4}}\left( TdR+2RdT\right) =2\left( \frac{dR}{R}+2\frac{dT}{T} \right) =2\frac{\Delta R}{R}+4\frac{\Delta T}{T}\\[4pt] &=&\frac{2(0.08\times 10^{8})}{6.94\times 10^{8}}+\frac{4(100)}{4800}\approx 0.106 \end{eqnarray*}
The percent increase in luminosity will be approximately 10.6\%.
Incidentally, a reasonable, although rough, estimate of how this change would affect Earth’s temperature is \Delta T_{e}\approx \left( \frac{1}{4}\right) (0.106)T_{e}=(0.0265)(290\rm{K})\approx 7.69\rm{K}
That is, the average temperature of Earth’s surface will change from 16.9 ^{\circ}{\rm C} (62.4^{\circ}{\rm F}) to 24.6^{\circ}{\rm C} (76.3^{\circ}{\rm F}). Such a change in temperature would be enough to modify Earth’s climate.

EXAMPLE 6Using the Differential in Error Analysis
A cola company requires a can in the shape of a right circular cylinder of height 10~\rm{cm} and radius 3~\rm{cm}. If the manufacturer of the cans claims a percentage error of no more than 0.2\% in the height and no more than 0.1\% in the radius, what is the approximate maximum variation in the volume of the can?
845
Solution The volume V of a right circular cylinder of height h~\rm{cm} and radius R\;\rm{cm} is V=\pi\;R^{2}h\;\rm{cm}^{3}. We find the differential dV. dV=\frac{\partial V}{\partial R}dR+\frac{\partial V}{\partial h}dh=2\pi\;Rh\,dR+\pi\;R^{2}dh
The relative error in the radius R is \dfrac{|\Delta R|}{R}=\dfrac{|dR|}{R}=0.001, and the relative error in the height h is \dfrac{\left\vert \Delta h\right\vert }{h}=\dfrac{|dh|}{h}=0.002. The relative error in the volume V is \begin{eqnarray*} \frac{|\Delta V|}{V} &\approx &\frac{|dV|}{V}=\frac{\left\vert 2\pi Rh\, dR+\pi R^{2} dh\right\vert }{\pi R^{2}h}=\left\vert 2\dfrac{dR}{R}+\dfrac{dh}{h}\right\vert\\[4pt] &=&\left\vert 2\dfrac{\Delta R}{R}+\dfrac{\Delta h}{h} \right\vert \leq 2\frac{\left\vert \Delta R\right\vert }{R}+\frac{\left\vert \Delta h\right\vert }{h} \\ &=&2(0.001)+0.002=0.004 \end{eqnarray*}
The maximum variation in the volume is approximately 0.4\%, so the actual volume of the container varies as follows: \begin{equation*} V=\pi R^{2}h\pm 0.004( \pi R^{2}h) =\pi R^2 h ( 1\pm 0.004) =90\pi ( 1\pm 0.004) \rm{cm}^{3} \end{equation*}
The volume V is between 89.64\pi \approx 281.612\;\rm{cm}^{3} and 90.36\pi \approx 283.874\rm{cm}^{3}.
NOW WORK
Continuity and Differentiability for Functions of Two Variables
Differentiable functions of a single variable are necessarily continuous. This result is also true for functions of two variables.
THEOREM Differentiability Is Sufficient for Continuity
Let z=f(x,y) be a function of two variables whose domain is D. Let (x_{0},y_{0}) be an interior point of D. If f is differentiable at (x_{0},y_{0}), then f is continuous at (x_{0},y_{0}).
Proof
The function z=f(x,y) is continuous at (x_{0},y_{0}) if \lim\limits_{(x,y) \rightarrow (x_{0},y_{0}) }f(x,y) =f(x_{0},y_{0}) . This is equivalent to the statement \lim\limits_{(x,y) \rightarrow (x_{0},y_{0}) }\Delta z=0. Since z=f(x,y) is differentiable at (x_{0},y_{0}), then \Delta z can be expressed as \begin{equation*} \Delta z=f_{x}(x_{0},y_{0})\Delta x+f_{y}(x_{0},y_{0})\Delta y+\eta _{1}\Delta x+\eta _{2}\Delta y \end{equation*}
where \lim\limits_{(\Delta x, \Delta y)\rightarrow (0, 0)}\eta _{1}=0 and \lim\limits_{(\Delta x, \Delta y)\rightarrow (0, 0)}\eta _{2}=0. Then \begin{equation*} \Delta z=\left[ f_{x}(x_{0}, y_{0})+\eta _{1}\right] \,\Delta x+\left[ f_{y}(x_{0}, y_{0})+\eta _{2}\right] \,\Delta y \end{equation*}
Now let \Delta x=x-x_{0} and \Delta y=y-y_{0}. Then (\Delta x,\Delta y)\rightarrow (0, 0) is equivalent to (x,y)\rightarrow (x_{0}, y_{0}) and \begin{eqnarray*} \lim_{(x, y)\rightarrow (x_{0}, y_{0})}\Delta z&=&\lim_{(x, y)\rightarrow (x_{0}, y_{0})}\{ [ f_{x}(x_{0}, y_{0})+\eta _{1} ] (x-x_{0} )\\[4pt] &&+\, [ f_{y}(x_{0}, y_{0})+\eta _{2} ](y-y_{0})\} =0 \end{eqnarray*}
That is, f is continuous at (x_{0},y_{0}).
For functions of two variables, differentiability implies continuity. However, the existence of partial derivatives at a point does not necessarily result in continuity at that point because f_{x} and/or f_{y} might not be continuous at the point. For example, the function \begin{equation*} f(x,y)=\left\{ \begin{array}{@{}c@{\quad}c@{\quad}c} \dfrac{xy}{x^{2}+y^{2}} & \hbox{if} & (x,y)\neq (0,0) \\ {\small 0} & \hbox{if} & (x,y)=(0,0) \end{array} \right. \end{equation*}
846
has partial derivatives at (0,0) , but as shown in Example 8 on page 835, f is not continuous at (0,0).
A function that is differentiable at (x_{0},y_{0}) is continuous at (x_{0},y_{0}) . So, a function that is not continuous at (x_{0},y_{0}) is not differentiable at (x_{0},y_{0}).
The following corollary provides a condition for z=f(x,y) to be continuous.
COROLLARY Continuity of a Function of Two Variables
Let z=f(x,y) be a function of two variables whose domain is D. Let (x_{0},y_{0}) be an interior point of D. If the partial derivatives f_{x} and f_{y} exist at each point of some disk centered at (x_{0},y_{0}), and if f_{x} and f_{y} are each continuous at (x_{0},y_{0}), then f is continuous at (x_{0},y_{0}).
Although the precise formulations are given as theorems, the following summary might be helpful:
If z=f(x,y),
- The continuity of the partial derivatives f_{x} and f_{y} implies the differentiability of f.
- The differentiability of f implies the continuity of f.
- The continuity of the partial derivatives f_{x} and f_{y} implies the continuity of f.
- The existence of the partial derivatives f_{x} and f_{y} does not necessarily mean f is differentiable.
- The existence of the partial derivatives f_{x} and f_{y} does not necessarily mean f is continuous.
4 Find the Differential of a Function of Three or More VariablesPrinted Page 846
Under suitable conditions, the definitions and theorems involving the differentiability of a function of two variables extend to functions of three or more variables. If w=f(x,y,z) is a function of three variables, the function f is differentiable at a point (x_{0},y_{0},z_{0}) if the change \Delta w in w can be expressed in the form \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ \Delta w=f_{x}(x, y, z)\Delta x+f_{y}(x, y, z)\Delta y+f_{z}(x, y, z)\Delta z+\eta _{1}\Delta x+\eta _{2}\Delta y+\eta _{3}\Delta z }}
where \eta _{1}, \eta _{2}, and \eta _{3} are each functions of \Delta x, \Delta y, and \Delta z for which \lim_{(\Delta x, \Delta y, \Delta z)\rightarrow (0, 0, 0)}\eta _{1}=0\quad\hbox{and}\!\!\quad \lim_{(\Delta x, \Delta y, \Delta z)\rightarrow (0, 0, 0)}\eta _{2}=0\quad\hbox{and}\!\!\quad \lim_{(\Delta x, \Delta y, \Delta z)\rightarrow (0, 0, 0)}\eta _{3}=0
If w=f(x,y,z) is differentiable at a point (x_{0},y_{0},z_{0}), the differentials dx, dy, and dz are defined as dx=\Delta x\qquad dy=\Delta y \qquad dz=\Delta z
The differential dw is defined as \bbox[5px, border:1px solid black, #F9F7ED]{\bbox[#FAF8ED,5pt]{ dw=f_{x}(x_{0},y_{0},z_{0})\ dx+f_{y}(x_{0},y_{0},z_{0})\ dy+f_{z}(x_{0},y_{0},z_{0})\ dz }}
It can be shown that if w=f(x,y,z) is defined within a ball centered at (x_{0},y_{0},z_{0}), and if the partial derivatives f_{x}, f_{y}, and f_{z} exist in this ball and are continuous at (x_{0},y_{0},z_{0}), then f is differentiable at (x_{0},y_{0},z_{0}).
EXAMPLE 7Finding the Differential of a Function of Three Variables
Find the differential dw of the function w=f(x,y,z)=3x^{2}\sin ^{2}y\cos z.
Solution The function f is defined everywhere in space. We begin by finding the partial derivatives of f. \begin{eqnarray*} f_{x}(x,y,z) &=&6x\;\sin^{2}\;\!y\;\cos\;z\qquad f_{y}(x,y,z) =6x^{2}\;\sin\;y\;\cos\;y\cos\;z\\ f_{z}(x,y,z) &=&-3x^{2}\sin^{2}\;\!y\;\sin\;z \end{eqnarray*}
847
Since the partial derivatives are continuous everywhere, we have \begin{eqnarray*} dw&=&f_{x}(x,y,z)\ dx+f_{y}(x,y,z)\ dy+f_{z}(x,y,z)\ dz\\ &=&6x\;\sin^{2}\;\!y\;\cos\;z\,dx+6x^{2}\;\sin\;y\;\cos\;y\;\cos\;z\,dy-3x^{2}\;\sin^{2}\;\!y\;\sin\;z\,dz \end{eqnarray*}
NOW WORK
The discussion above extends to functions of more than three variables in an analogous way.