6.3 Volume of a Solid of Revolution: Cylindrical ShellsPrinted Page 424
OBJECTIVES
When you finish this section, you should be able to:
- Use the shell method to find the volume of a solid formed by revolving a region about the y-axis (p. 425)
- Use the shell method to find the volume of a solid formed by revolving a region about the x-axis (p. 428)
- Use the shell method to find the volume of a solid formed by revolving a region about a line parallel to a coordinate axis (p. 430)
There are solids of revolution for which the volume is difficult to find using the disk or washer method. In these situations, the volume can often be found using cylindrical shells.
NOTE
Sewer lines and the water pipes in a house are cylindrical shells.
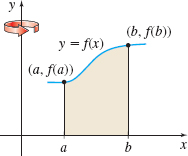
A cylindrical shell is the solid between two concentric cylinders, as shown in Figure 28. If the inner radius of the cylinder is r and the outer radius is R, the volume V of a cylindrical shell of height h is \begin{align*} \bbox[5px, border:1px solid black, #F9F7ED]{ V=\pi R^{2}h-\pi r^{2}h } \end{align*}

That is, the volume of a cylindrical shell equals the volume of the larger cylinder, which has radius R, minus the volume of the smaller cylinder, which has radius r. It is convenient to write this formula as V=\pi ( R^{2}-r^{2}) h=\pi (R+r)(R-r)h=2\pi\! \left( \dfrac{R+r}{2}\right) h(R-r) \begin{equation*} \bbox[5px, border:1px solid black, #F9F7ED]{ V=2\pi\! \left( \dfrac{R+r}{2}\right) h(R-r)} \end{equation*} V=2\pi \hbox{ (Average radius) (Height) (Thickness)}
1 Use the Shell Method to Find the Volume of a Solid Formed by Revolving a Region About the y-AxisPrinted Page 425
425
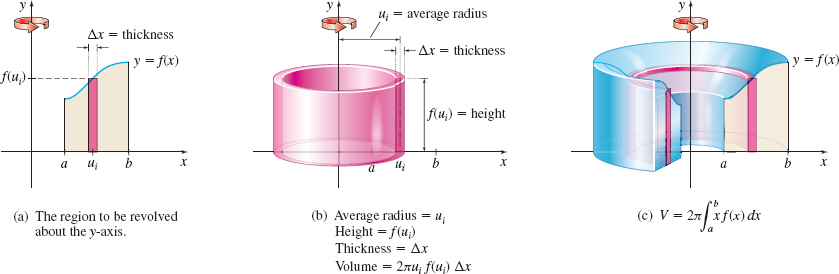
Suppose a function y=f(x) is nonnegative and continuous on the closed interval [a,b], where a\geq 0. We seek the volume V of the solid generated by revolving the region bounded by the graph of f, the x-axis, and the lines x=a and x=b about the y-axis. See Figure 29.
We begin by partitioning the interval [a,b] into n subintervals: \begin{equation*} \lbrack a,x_{1}], [x_{1},x_{2}], \ldots , [x_{i-1},x_{i}],\ldots , [x_{n-1},b] \end{equation*}
each of width \Delta x=\dfrac{b-a}{n}. We concentrate on the rectangle whose base is the subinterval [x_{i-1}, x_{i}] and whose height is f(u_{i}), where u_{i}=\dfrac{x_{i-1}+x_{i}}{2} is the midpoint of the subinterval. See Figure 30(a). When this rectangle is revolved about the y-axis, it generates a cylindrical shell of average radius u_{i}, height f(u_{i}), and thickness \Delta x, as shown in Figure 30(b). The volume V_{i} of this cylindrical shell is V_{i}= 2\pi \hbox{(Average radius)(Height)(Thickness)} =2\pi u_{i}f(u_{i})\Delta x
The sum of the volumes of the n cylindrical shells approximates the volume V of the solid generated by revolving the region bounded by the graph of y=f(x), the x-axis, and the lines x=a and x=b about the y-axis. That is, V\approx \sum\limits_{i=1}^{n}[ 2\pi u_{i} f(u_{i})\Delta x] =2\pi \sum\limits_{i=1}^{n}[u_{i} f(u_{i})\Delta x]
As the number n of subintervals increases, the sums 2\pi \sum\limits_{i=1}^{n}\left[ u_{i} f(u_{i})\Delta x\right] become better approximations to the volume V of the solid. These sums are Riemann sums, and since f is continuous on [a,b], the limit is a definite integral. See Figure 30(c). When cylindrical shells are used to find the volume of a solid of revolution, we refer to the process as the shell method.
Volume of a Solid of Revolution About the y-Axis: the Shell Method
If y=f(x) is a function that is continuous and nonnegative on the closed interval [a,b], where a\geq 0, then the volume V of the solid generated by revolving the region bounded by the graph of f, the x-axis, and the lines x = a and x = b about the y-axis is \begin{equation*} \bbox[5px, border:1px solid black, #F9F7ED]{ V=2\pi \int_{a}^{b}x f(x)~{\it dx}} \end{equation*}
426
It can be shown that the shell method and the washer method of Section 6.2 are equivalent; that is, they both give the same answer.* The advantage of having two equivalent, yet different, formulas is flexibility. There are times when one of the two methods is easier to use, as Example 1 illustrates.
EXAMPLE 1Finding the Volume of a Solid: Revolving About the y-Axis
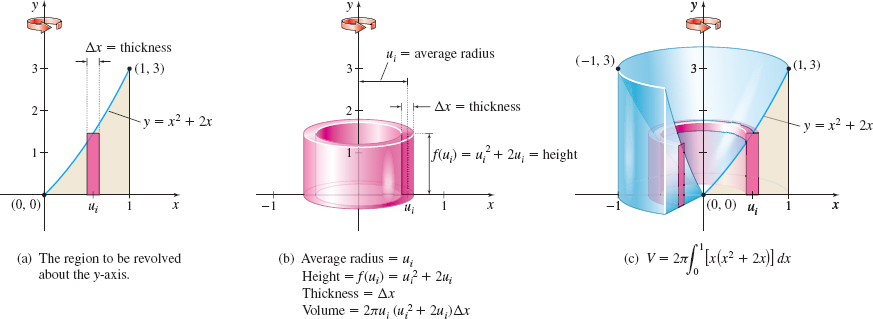
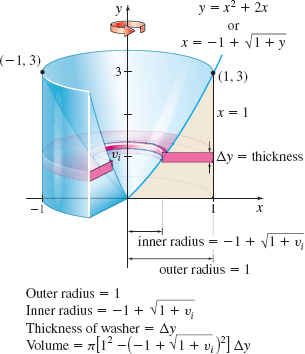
Find the volume V of the solid generated by revolving the region bounded by the graphs of f(x) =x^{2}+2x, the x-axis, and the line x=1 about the y-axis.
Solution Using the shell method: In the shell method, when a region is revolved about the y-axis, we partition the x-axis and use vertical shells. Figure 31(a) illustrates the region to be revolved and a typical rectangle of height f(u_{i}) and thickness \Delta x that will become a shell with average radius u_{i} when it is revolved about the y-axis. The volume of a typical shell is V_{i}=2\pi (Average radius)(Height)(Thickness) =2\pi u_{i} f(u_{i})\Delta x, as shown in Figure 31(b). Figure 31(c) illustrates the solid of revolution. The volume V of the solid of revolution is \begin{eqnarray*} V&=&2\pi \int_{0}^{1}xf(x) {\it dx}=2\pi \int_{0}^{1}[ x(x^{2}+2x) ] ~{\it dx}=2\pi \int_{0}^{1}(x^{3}+2x^{2})~{\it dx}\\[4pt] &=&2\pi\! \left[ \dfrac{x^{4}}{4}+ \dfrac{2x^{3}}{3}\right] _{0}^{1}=\dfrac{11\pi }{6}\hbox{ cubic units} \end{eqnarray*}
Using the washer method: Using the washer method, a revolution about the y-axis requires integration with respect to y. This means we need to find the inverse function of y=f(x). We treat x^{2}+2x-y=0 as a quadratic equation in the variable x and use the quadratic formula with a=1, b=2, and c=-y to obtain x=g(y)=-1\pm \sqrt{1+y}. Since x\geq 0, we use the + sign.
See Figure 32. The volume of a typical washer is V_{i}=\pi [ (\hbox{Outer radius}) ^{2}-( \hbox{Inner radius}) ^{2}]\times (\hbox{Thickness}).
The volume V of the solid of revolution is \begin{eqnarray*} V &=&\pi \int_{0}^{3} [ 1^{2}- ( -1+\sqrt{1+y}) ^{2}] ~{\it dy}=\pi \int_{0}^{3} [ 1- ( 1-2\sqrt{1+y}+1+y) ] ~{\it dy}\\[4pt] &=&\pi \int_{0}^{3} [ 2\sqrt{1+y}-1-y]\, {\it dy} =\pi \int_{0}^{3} ( 2\sqrt{1+y}) {\it dy}-\pi \int_{0}^{3}(1+y)~{\it dy} \end{eqnarray*}
*This topic is discussed in detail in an article by Charles A. Cable (February 1984), “The Disk and Shell Method,” American Mathematical Monthly, 91(2), 139.
427
The two integrals are found as follows:
- \pi \displaystyle \int_{0}^{3}(2\sqrt{1+y})~ {\it dy} \underset{\underset{\underset{\color{#0066A7}{\hbox{then \({du}={dy}\)}}}{\color{#0066A7}{\hbox{Let \(u=1+y\);}}}}{\color{#0066A7}{\uparrow }}} {=} 2\pi \displaystyle \int_{1}^{4}u^{1/2}\ {\it du}=2\pi \left[ \dfrac{u^{3/2}}{\dfrac{3}{2}}\right]_{1}^{4}=\dfrac{28\pi }{3}
- \pi \displaystyle \int_{0}^{3}(1+y)~{\it dy}=\pi \left[ y+\dfrac{y^{2}}{2}\right] _{0}^{3}= \dfrac{15\pi }{2}
The volume V is V=\frac{28\pi }{3}-\frac{15\pi }{2}=\frac{11\pi }{6}\hbox{ cubic units}
NOW WORK
Example 1 gives a clue to when the shell method is preferable to the washer method. When it is difficult, or impossible, to solve y=f(x) for x, we use the shell method. For example, if the function in Example 1 had been y=f(x) =x^{5}+x^{2}+1, we would not have been able to solve for x, so the practical choice is the shell method.
The next example illustrates the importance of sketching a graph before using a formula. Notice the limits of integration and how we determined them when we use the washer method.
EXAMPLE 2Finding the Volume of a Solid: Revolving About the y-Axis
Find the volume V of the solid generated by revolving the region bounded by the graphs of f(x) =x^{2} and g(x) =12-x to the right of x=1 about the y-axis.
Solution Using the shell method: Figure 33(a) shows the graph of the region to be revolved and a typical rectangle.
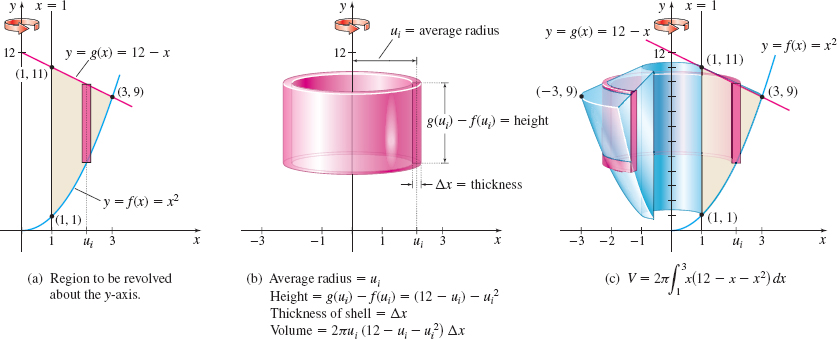
As shown in Figure 33(b), in the shell method, we partition the x-axis and use vertical shells. A typical shell has height h_{i}=g( u_{i}) -f( u_{i}) =(12-u_{i})-u_{i}^{2}=12-u_{i}-u_{i}^{2}, and volume V_{i}=2\pi u_{i}( 12-u_{i}-u_{i}^{2}) \Delta x. Figure 33(c) shows the solid of revolution. Notice that the integration takes place from x=1 to x=3. The volume V of the solid of revolution is \begin{eqnarray*}\hskip-1pc V &=&2\pi \int_{1}^{3}x(12-x-x^{2})~{\it dx}=2\pi \int_{1}^{3}( 12x-x^{2}-x^{3}) ~{\it dx}=2\pi \left[ 6x^{2}-\dfrac{x^{3}}{3}-\dfrac{x^{4}}{ 4}\right] _{1}^{3} \\[4pt] &=&2\pi\! \left[ \left( 54-9-\dfrac{81}{4}\right) -\left( 6-\dfrac{1}{3}- \dfrac{1}{4}\right) \right] =\dfrac{116~\pi }{3}\hbox{ cubic units} \end{eqnarray*}
428
Using the washer method: Figure 34 shows the solid of revolution and typical washers.
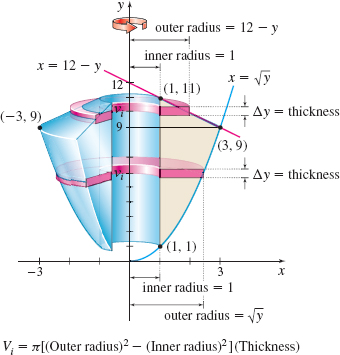
In the washer method, we partition the interval \left[ 1,11\right] on the y-axis and use horizontal washers. At y=9, the function on the right changes. The volume of a typical washer in the interval [1,9] is \begin{equation*} V_{i}=\pi \big[ \sqrt{v_{i}}^{2}-1^{2}\big] \Delta y=\pi (v_{i}-1) \Delta y \end{equation*}
The volume of a typical washer in the interval [9,11] is \begin{equation*} V_{i}=\pi \big[ ( 12-v_{i}) ^{2}-1^{2}\big] \Delta y=\pi \big( 143-24v_{i}+v_{i}^{2}\big) \Delta y \end{equation*}
The volume V of the solid of revolution is \begin{eqnarray*} V &=&\pi \int_{1}^{9}(y-1) ~{\it dy}+\pi \int_{9}^{11} (143-24y+y^{2})~{\it dy}\\[8pt] &=&\pi \left[ \dfrac{y^{2}}{2}-y\right] _{1}^{9}+\pi \left[ 143y-12y^2 +\dfrac{y^{3}}{3} \right] _{9}^{11}\hbox{ } \notag \\[8pt] &=&\pi \left[ \left( \dfrac{81}{2}-9\right) -\left( \dfrac{1}{2}-1\right) \right] +\pi \left( 143\left( 2\right) -(12)(121-81)+\dfrac{11^{3}}{3}-\dfrac{9^{3}}{3}\right)\\[8pt] &=&32\pi +\dfrac{20}{3}\pi =\dfrac{116\,\pi }{3}\hbox{ cubic units} \end{eqnarray*}
NOW WORK
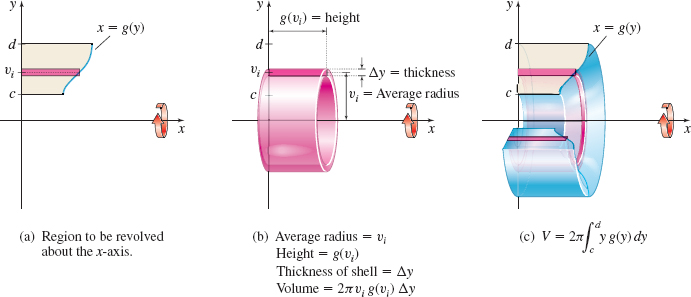
2 Use the Shell Method to Find the Volume of a Solid Formed by Revolving a Region About the x-AxisPrinted Page 428
Figure 35(a) on page 429 shows a region that is to be revolved about the x-axis, Figure 35(b) shows a typical shell, and Figure 35(c) shows the solid of revolution.
429
Volume of a Solid of Revolution About the x-Axis: the Shell Method
If x=g(y) is a function that is continuous and nonnegative on the closed interval [c,d], c\geq 0, the volume V of the solid generated by revolving the region bounded by the graphs of x=g(y), the y-axis, and the lines y=c and y=d about the x-axis is \begin{equation*} \bbox[5px, border:1px solid black, #F9F7ED]{ V=2\pi \int_{c}^{d}y~ g(y)~{\it dy}} \end{equation*}
EXAMPLE 3Using the Shell Method: Revolving About the x-Axis
Find the volume V of the solid generated by revolving the region bounded by the graph of, \dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1, a > 0, b > 0, in the first quadrant, about the x-axis.
NEED TO REVIEW?
The equation of an ellipse is discussed in Appendix A.3, pp. A-23 to A-24.
Solution The equation \dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1 defines an ellipse. The intercepts of its graph are (a,0), (0,b), (-a,0), and (0,-b). The region to be revolved is the shaded region in the first quadrant shown in Figure 36(a).

In the shell method, when the region is revolved about the x-axis, we partition the y-axis and use horizontal shells. A revolution about the x-axis requires integration with respect to y, so we express the equation of the ellipse as x=g(y)=\dfrac{a}{b}\sqrt{~b^{2}-y^{2}}
430
The volume of a typical shell is V_{i}=2\pi\ \hbox{(Average radius)(Height)(Thickness)} = 2\pi v_{i}g(v_{i})\Delta y
See Figure 36(b).
Figure 36(c) shows the solid of revolution. The volume V of the solid of revolution is \begin{eqnarray*} V &=&2\pi \int_{0}^{b}y~g(y)~{\it dy}=2\pi \int_{0}^{b}y\left( \dfrac{a}{b}\sqrt{ b^{2}-y^{2}}\right) {\it dy} \underset{\underset{\underset{\color{#0066A7}{\hbox{then \({du}={-2y}{ dy}\)}}}{\color{#0066A7}{\hbox{Let \(u=b^2-y^2\);}}}}{\color{#0066A7}{\uparrow }}} {=} 2\pi \dfrac{a}{b}\left( -\dfrac{1}{2}\right) \int_{b^{2}}^{0}\sqrt{u}\ {\it du} \\[-9pt] &=&\dfrac{\pi a}{b}\int_{0}^{b^{2}}u^{1/2}~{\it du}=\dfrac{\pi a}{b}\left[ \dfrac{ u^{3/2}}{\dfrac{3}{2}}\right] _{0}^{b^{2}}=\dfrac{2\pi a}{3b}( b^{3}) =\dfrac{2\pi ab^{2}}{3}\hbox{ cubic units} \end{eqnarray*}
NOW WORK
Using symmetry, the volume V of the ellipsoid generated by revolving y = \dfrac{b}{a}\sqrt{a^{2}-x^{2}}, -a\leq x\leq a, about the x-axis is twice the volume found in Example 3, namely V=\dfrac{4}{3}\pi ab^{2}.
If, in Example 3, a=b, then the solid generated is a hemisphere whose volume is \dfrac{2\pi a^{3}}{3} cubic units. By symmetry, the volume of a sphere of radius R, (a=b=R), is \dfrac{4\pi R^{3}}{3} cubic units.
3 Use the Shell Method to Find the Volume of a Solid Formed by Revolving a Region About a Line Parallel to a Coordinate AxisPrinted Page 430
EXAMPLE 4Using the Shell Method: Revolving About the Line x=2
Find the volume V of the solid of revolution generated by revolving the region bounded by the graph of y=2x-2x^{2} and the x-axis about the line x=2.
Solution The region bounded by the graph of y=2x-2x^{2} and the x-axis is illustrated in Figure 37(a). A typical shell formed by revolving the region about the line x=2, as shown in Figure 37(b), has an average radius of 2-u_{i}, height f(u_{i}) = 2u_{i}-2u_{i}^{2}, and thickness \Delta x. The solid of revolution is depicted in Figure 37(c).
431
The volume V of the solid is \begin{eqnarray*} V&=&2\pi \displaystyle \int_{0}^{1}(2-x)(2x-2x^{2})~{\it dx}=4\pi \displaystyle \int_{0}^{1}(x^{3}-3x^{2}+2x)~{\it dx}\\[4pt] &=&4\pi \left[ \dfrac{x^{4}}{4}-x^{3}+x^{2} \right] _{0}^{1}=\pi \hbox{ cubic units} \end{eqnarray*}
NOW WORK
Summary
The Volume V of a Solid of Revolution
| Washer Method | Shell Method | |
|---|---|---|
|
Partition the x-axis; use vertical washers. |
Partition the y-axis; use horizontal shells. |
|
Partition the y-axis; use horizontal washers. |
Partition the x-axis; use vertical shells. |