OBJECTIVES

When you finish this section, you should be able to:

1. Integrate a rational function whose denominator contains only distinct linear factors (p. 500)
2. Integrate a rational function whose denominator contains a repeated linear factor (p. 502)
3. Integrate a rational function whose denominator contains a distinct irreducible quadratic factor (p. 503)
4. Integrate a rational function whose denominator contains a repeated irreducible quadratic factor (p. 504)

NEED TO REVIEW?

Rational functions are discussed in Section P.2, pp. 19-20.

Case 1: If the denominator $q$ contains only distinct linear factors, say, $x-a_{1}$, $x-a_{2}, \ldots , x-a_{n}$, then $\dfrac{p}{q}$ can be written as $$\bbox[5px, border:1px solid black, #F9F7ED]{\dfrac{p(x)}{q(x)}= \dfrac{A_{1}}{x-a_{1}}+\dfrac{A_{2}}{x-a_{2}}+\cdots +\dfrac{A_{n}}{x-a_{n}}}\tag{1}$$

where $A_{1}, A_{2}, \ldots , A_{n}$ are real numbers.

EXAMPLE 1Integrating a Rational Function Whose Denominator Contains Only Distinct Linear Factors

Find $\int \dfrac{x\,dx}{x^{2}-5x+6}$.

Solution The integrand is a proper rational function in lowest terms. We begin by factoring the denominator: $x^{2}-5x+6=(x-2)(x-3)$. Since the factors are linear and distinct, we apply Case 1 and allow for the terms $\dfrac{A}{x-2}$ and $\dfrac{B}{x-3}$. $$\dfrac{x}{(x-2)(x-3)}=\dfrac{A}{x-2}+\dfrac{B}{x-3}$$

Now we clear fractions by multiplying both sides of the equation by $(x-2)(x-3).$ $$\begin{eqnarray*} \begin{array}{ll@{\qquad}l} x &= A(x-3)+B(x-2) \\[3pt] x &= (A+B)x-( 3A+2B) & {\color{#0066A7}{\hbox{Group like terms.}}} \end{array} \end{eqnarray*}$$

This is an identity in $x$, so the coefficients of like powers of $x$ must be equal. $$\begin{eqnarray*} \begin{array}{ll@{\qquad}l} 1 &= A+B & {\color{#0066A7}{\hbox{The coefficient of }{x}\hbox{ equals 1.}}} \\[3pt] 0 &= -3A-2B & {\color{#0066A7}{\hbox{The constant term on the left is 0.}}} \end{array} \end{eqnarray*}$$

This is a system of two equations containing two variables. Solving the second equation for $B,$ we get $B = -\dfrac{3}{2}A.$ Substituting for $B$ in the first equation produces the solution $A$ = -2 from which $B$ = 3. So, $$\dfrac{x}{(x-2)(x-3)}=\dfrac{-2}{x-2}+\dfrac{3}{x-3}$$

Then $$\begin{eqnarray*} \int \dfrac{x}{(x-2)(x-3)}dx &=& \int \dfrac{-2}{x-2}\,dx+\int \dfrac{3}{x-3} \,dx \\ &=& -2\,\ln \,\vert x-2 \vert +3\ln \,\vert x-3 \vert +C=\ln \left\vert \dfrac{(x-3)^{3}}{(x-2)^{2}}\right\vert +C \end{eqnarray*}$$

NOW WORK

Problem 11.

EXAMPLE 2Deriving Formulas Involving a Rational Function

Derive these formulas: $$\bbox[5px, border:1px solid black, #F9F7ED]{{(a)} \quad \int \dfrac{dx}{x^{2}-a^{2}}=\dfrac{1}{2a}\ln \left \vert \dfrac{x-a}{x+a}\right \vert +C \quad a ≠ 0 }$$ $$\bbox[5px, border:1px solid black, #F9F7ED]{{(b)} \quad \int \dfrac{dx}{a^{2}-x^{2}}=\dfrac{1}{2a}\ln \left\vert \dfrac{x+a}{x-a}\right\vert +C \quad a ≠ 0 }$$

Solution  (a) The factored denominator $x^{2}-a^{2}=( x-a) (x+a)$ contains only distinct linear factors. So, $\dfrac{1}{x^{2}-a^{2}}$ can be decomposed into partial fractions of the form $$\begin{eqnarray*} \begin{array}{rl@{\qquad}l} \dfrac{1}{x^{2}-a^{2}} &= \dfrac{1}{(x-a)(x+a)}=\dfrac{A}{x-a}+\dfrac{B}{x+a}\\ 1 &= A(x+a) +B (x-a)&{\color{#0066A7}{\hbox{Multiply both sides by }(x-a) (x+a).}} \end{array} \end{eqnarray*}$$

This is an identity in $x.$ When $x=a,$ the term involving $B$ drops out. Then $1=A(2a)$, so $A=\dfrac{1}{2a}.$ When $x=-a$, the term involving $A$ drops out. Then $1=B (-2a)$, so $B=-\dfrac{1}{2a}.$ Then, $$\begin{equation*} \dfrac{1}{x^{2}-a^{2}}=\dfrac{A}{x-a}+\dfrac{B}{x+a}=\dfrac{1}{2a( x-a) }-\dfrac{1}{2a(x+a) } \end{equation*}$$ $$\begin{eqnarray*} \int \dfrac{dx}{x^{2}-a^{2}} &=& \dfrac{1}{2a}\int \dfrac{dx}{x-a}-\dfrac{1}{2a} \int \dfrac{dx}{x+a}=\dfrac{1}{2a}\left( \int \dfrac{dx}{x-a}-\int \dfrac{dx}{x+a}\right) \\[7pt] &=& \dfrac{1}{2a}\big(\ln \,\vert x-a\vert -\ln \,\vert x+a \vert\big) +C\\[7pt] &=&\dfrac{1}{2a}\ln \left\vert \dfrac{x-a}{x+a}\right\vert +C \end{eqnarray*}$$

(b) Using the result from (a), we get $$\begin{eqnarray*} \int \dfrac{dx}{a^{2}-x^{2}} &=& -\int \dfrac{dx}{x^{2}-a^{2}}=-\dfrac{1}{2a}\ln \left\vert \dfrac{x-a}{x+a}\right\vert +C=\dfrac{1}{2a}\ln \left\vert \dfrac{x-a }{x+a}\right\vert ^{-1}+C \\[6pt] &=& \dfrac{1}{2a}\ln \left\vert \dfrac{x+a}{x-a}\right\vert +C \end{eqnarray*}$$

NOW WORK

Problem 37.

Case 2: If the denominator $q$ has a repeated linear factor $(x-a)^{n},$ $n \geq 2$ an integer, then the decomposition of $\dfrac{p}{q}$ includes the terms $$\bbox[5px, border:1px solid black, #F9F7ED]{ \dfrac{A_{1}}{x-a}, \dfrac{A_{2}}{(x-a)^{2}},\ \ldots ,\ \dfrac{A_{n}}{(x-a)^{n}}}$$

where $A_{1},$ $A_{2,}$ $\ldots ,$ $A_{n}$ are real numbers.

EXAMPLE 3Integrating a Rational Function Whose Denominator Contains a Repeated Linear Factor

Find $\int \dfrac{dx}{x(x-1)^{2}}$.

Solution  Since $x$ is a distinct linear factor of the denominator $q$, and $(x-1)^{2}$ is a repeated linear factor of the denominator, the decomposition of $\dfrac{1}{x(x-1) ^{2}}$ into partial fractions has the three terms $\dfrac{A}{x}$, $\dfrac{B}{x-1},$ and $\dfrac{C}{(x-1) ^{2}}$. $$\begin{eqnarray*} \begin{array}{rl@{\!\!\!\qquad}l} \dfrac{1}{x(x-1)^{2}} &= \dfrac{A}{x}+\dfrac{B}{x-1}+\dfrac{C}{(x-1)^{2}} \quad &{\color{#0066A7}{\hbox{Write the identity.}}} \\ 1 &= A(x-1)^{2}+B\cdot x(x-1)+C\cdot x\quad &{\color{#0066A7}{\hbox{Multiply both sides by }{x} (x-1)^{2}.}} \end{array} \end{eqnarray*}$$

We find $A,$ $B,$ and $C$ by choosing values of $x$ that cause one or more terms to drop out. When $x=1,$ we have $1=C\cdot 1,$ so $C=1$. When $x=0,$ we have $1=A(0-1)^{2},$ so $A=1.$ Now using $A=1$ and $C=1,$ we have $$\begin{equation*} 1=(x-1)^{2}+B\cdot x(x-1)+ 1 \cdot x \end{equation*}$$

Suppose we let $x=2.$ (Any choice other than $0$ and $1$ will also work.) Then $$\begin{eqnarray*} 1 &=&1+2B+2 \\ B &=&-1 \end{eqnarray*}$$

Then $$\begin{array}{l@{\qquad}l} \dfrac{1}{x(x-1)^{2}}=\dfrac{1}{x}+\dfrac{-1}{(x-1) }+\dfrac{1}{(x-1)^{2}} \quad{\color{#0066A7}{\hbox{\(A=1\)}}\quad \quad{\color{#0066A7}{\hbox{\(B=-1\)}}}\quad \quad{\color{#0066A7}{\hbox{\(C=1\)}}}} \end{array}$$

So, $$\begin{eqnarray*} \int \dfrac{dx}{x(x-1)^{2}} &=& \int \dfrac{dx}{x}- \int \dfrac{dx}{x-1}+ \int \dfrac{dx}{(x-1)^{2}}\\[7pt] &=& \ln \vert x \vert -\ln \vert x-1\vert -\dfrac{1}{x-1} +C_{1} \end{eqnarray*}$$

NOTE

To avoid confusion, we use $C_{1}$ for the constant of integration whenever $C$ appears in the partial fraction decomposition.

NOW WORK

Problem 15.

NEED TO REVIEW?

The discriminant of a quadratic equation is discussed in Appendix A.1, pp. A-3 to A-4.

Case 3: If the denominator $q$ contains a nonrepeated irreducible quadratic factor $ax^{2}+bx+c$, then the decomposition of $\dfrac{p}{q}$ includes the term $$\bbox[5px, border:1px solid black, #F9F7ED]{ \dfrac{Ax+B}{ax^{2}+bx+c} }$$

where $A$ and $B$ are real numbers.

EXAMPLE 4Integrating a Rational Function Whose Denominator Contains a Distinct Irreducible Quadratic Factor

Find $\int \dfrac{3x}{x^{3}-1}\,dx$.

Solution  The denominator is $x^{3}-1=(x-1)(x^{2}+x+1)$. Since $x-1$ is a nonrepeated linear factor, by Case 1 the decomposition of $\dfrac{ 3x}{x^{3}-1}=\dfrac{3x}{(x-1) (x^{2}+x+1) }$ has the term $\dfrac{A}{x-1}$.

The discriminant of the quadratic equation $x^{2}+x+1=0$ is negative, so $x^{2}+x+1$ is an irreducible quadratic factor of $q$, and the decomposition of $\dfrac{p}{q}$ also contains the term $\dfrac{Bx+C}{x^{2}+x+1}$. Then $$\dfrac{3x}{x^{3}-1}=\dfrac{A}{x-1}+\dfrac{Bx+C}{x^{2}+x+1}$$

Clearing the denominators, we have $$\begin{equation*} 3x=A(x^{2}+x+1)+(Bx+C)(x-1)\ \end{equation*}$$

This is an identity in $x$. When $x=1$, we have $3=3A,$ so $A=1.$ With $A=1,$ the identity becomes $$\begin{eqnarray*} 3x &=& (x^{2}+x+1) + (Bx+C) (x-1) \\[3pt] -x^{2}+2x-1 &=& (Bx+C) (x-1) \\[3pt] -(x-1) ^{2} &=& (Bx+C) (x-1) \\[3pt] -(x-1) &=& Bx+C \\[3pt] B &=& -1,\quad C=1 \end{eqnarray*}$$

So, $$\begin{eqnarray*} \dfrac{3x}{x^{3}-1} &=&\dfrac{1}{x-1}+\dfrac{-x+1}{x^{2}+x+1} \nonumber\\[5pt] \int \dfrac{3x}{x^{3}-1}\,dx &=&\int \left( \dfrac{1}{x-1}+\dfrac{-x+1}{ x^{2}+x+1}\right) dx=\int \dfrac{1}{x-1}\,dx+\int \dfrac{-x+1}{x^{2}+x+1}\,dx \nonumber\\[5pt] &=& \ln \vert x-1\vert -\int \dfrac{x-1}{x^{2}+x+1}\, dx\tag{2} \end{eqnarray*}$$

To find the integral on the right, we complete the square in the denominator and use substitution. $$\begin{eqnarray*} \int \dfrac{x-1}{x^{2}+x+1}dx &=& \int \dfrac{x-1}{\left( x+\dfrac{1}{2}\right)^{2}+\dfrac{3}{4}}dx \underset{\underset{\color{#0066A7}{\hbox{\(u=x+\dfrac{1}{2}\)}}}{\color{#0066A7}{\left\uparrow{\vphantom{\vrule width0pc height11pt\\ depth0pt}}\right.}}} {=} \int \dfrac{u-\dfrac{3}{2}}{u^{2}+\dfrac{3}{4}}du=\int \dfrac{u}{u^{2}+\dfrac{3}{4\\ }}du-\dfrac{3}{2}\int \dfrac{du}{u^2+\dfrac{3}{4}} \\ &=& \dfrac{1}{2}\ln \left( u^{2}+\dfrac{3}{4}\right) -\dfrac{3}{2}\left[ \dfrac{2}{\sqrt{3}}\tan ^{-1}\left( \dfrac{2}{\sqrt{3}}u\right) \right] \quad {\color{#0066A7}{\hbox{\(\int \dfrac{du}{u^{2}+a^{2}}\, =\dfrac{1}{a}\tan^{-1}\left( \dfrac{u}{a}\right)\)}}} \\ &=& \dfrac{1}{2}\ln \left( u^{2}+\dfrac{3}{4}\right) -\sqrt{3}\tan ^{-1}\left( \dfrac{2}{\sqrt{3}}u\right) \\ &=& \dfrac{1}{2}\ln (x^{2}+x+1) -\sqrt{3}\tan ^{-1}\left( \dfrac{2x+1}{\sqrt{3}}\right) \end{eqnarray*}$$

Then from (2), $$\int \dfrac{3x}{x^{3}-1}dx=\ln \vert x-1\vert -\dfrac{1}{2}\ln \,(x^{2}+x+1)+\sqrt{3}\tan ^{-1}\left( \dfrac{2x+1}{\sqrt{3}}\right) +C_{1}$$

NOW WORK

Problem 21.

Case 4: If the denominator $q$ contains a repeated irreducible quadratic polynomial $(x^{2}+bx+c)^{n}$, $n \geq 2$ an integer, then the decomposition of $\dfrac{p}{q}$ includes the terms $$\bbox[5px, border:1px solid black, #F9F7ED]{ \dfrac{A_{1}x+B_{1}}{x^{2}+bx+c}\hbox{, }\ \dfrac{A_{2}x+B_{2}}{ (x^{2}+bx+c)^{2}}\hbox{,}\ \ldots\hbox{, }\ \dfrac{A_{n}x+B_{n}}{(x^{2}+bx+c)^{n}} }$$

where $A_{1}$, $B_{1}$, $A_{2}$, $B_{2}$, …, $A_{n}$, $B_{n}$ are real numbers.

EXAMPLE 5Integrating a Rational Function Whose Denominator Contains a Repeated Irreducible Quadratic Factor

Find $\int \dfrac{x^{3}+1}{(x^{2}+4)^{2}}\,dx$.

Solution  The denominator is a repeated, irreducible quadratic, so the decomposition of $\dfrac{x^{3}+1}{(x^{2}+4)^{2}}$ is $$\dfrac{x^{3}+1}{(x^{2}+4)^{2}}=\dfrac{Ax+B}{x^{2}+4}+\dfrac{Cx+D}{(x^{2}+4)^{2}}$$

Clearing fractions and combining terms give $$\begin{eqnarray*} x^{3}+1 &=& (Ax+B) (x^{2}+4) +Cx+D \\[3pt] x^{3}+1 &=& Ax^{3}+Bx^{2}+(4A+C)x+4B+D \end{eqnarray*}$$

Equating coefficients, we get $$\begin{equation*} \begin{array}{rl@{\qquad}rrr} A=1 \quad B=0\quad 4A+C &= 0 & 4B+D &= 1 \\[3pt] C &=-4 & D &=1 \end{array} \end{equation*}$$

Then $$\begin{equation*} \dfrac{x^{3}+1}{(x^{2}+4)^{2}}=\dfrac{x}{x^{2}+4}+\dfrac{-4x+1}{(x^{2}+4)^{2}} \end{equation*}$$

and $$\begin{eqnarray*} \int \dfrac{x^{3}+1}{(x^{2}+4)^{2}}dx &=& \int \dfrac{x}{x^{2}+4}dx+\int \dfrac{ -4x+1}{(x^{2}+4)^{2}}dx \nonumber\\[5pt] & =& \int \dfrac{x}{x^{2}+4}dx-4\int \dfrac{x}{(x^{2}+4)^{2} }dx+\int \dfrac{dx}{(x^{2}+4)^{2}}\tag{3} \end{eqnarray*}$$

In the first two integrals on the right in (3), we use the substitution $u=x^{2}+4$ , $x \geq 0.$ Then $du=2x\,dx$, and

• $\int \dfrac{x}{x^{2}+4}dx = \dfrac{1}{2}\int \dfrac{du}{u}=\dfrac{1}{2}\ln \vert u \vert =\dfrac{1}{2}\ln (x^{2}+4) \tag{4}$
• $-4\int \dfrac{x}{(x^{2}+4)^{2}}dx = -2\int \dfrac{\,du}{u^{2}}=\dfrac{2}{u}= \dfrac{2}{x^{2}+4}\tag{5}$

In the third integral on the right in (3), we use the trigonometric substitution $x=2\tan \theta$, $-\dfrac{\pi }{2} \lt \theta \lt \dfrac{\pi }{2}.$ Then $dx=2\sec ^{2} \theta \,d\theta$, and $$\begin{eqnarray*} \int \dfrac{dx}{(x^{2}+4)^{2}} &=& \int \dfrac{2\sec ^{2} \theta \,d\theta }{ \left( 4\tan ^{2}\theta +4\right) ^{2}}=\dfrac{2}{16}\int \dfrac{\sec ^{2} \theta \,d\theta }{( \sec ^{2} \theta) ^{2}}=\dfrac{1}{8}\int \cos ^{2}\theta \,d\theta \\[7pt] &=& \dfrac{1}{8}\int \dfrac{1+\cos (2\theta) }{2}d\theta \\[7pt] &=& \dfrac{1}{16}\left[ \theta +\dfrac{1}{2}\sin (2\theta ) \right] =\dfrac{1}{16}(\theta +\sin \theta \cos \theta ) \end{eqnarray*}$$

To express the solution in terms of $x$, either use the triangles in Figure 10 or use trigonometric identities as follows: $$\begin{equation*} \sin \theta \cos \theta =\dfrac{\sin \theta }{\cos \theta }\cdot \cos ^{2}\theta =\dfrac{\tan \theta }{\sec ^{2} \theta }=\dfrac{\tan \theta }{\tan ^{2}\theta +1}=\dfrac{\dfrac{x}{2}}{\dfrac{x^{2}}{4}+1}=\dfrac{2x}{x^{2}+4} \end{equation*}$$

Then $$\begin{eqnarray*} \int \dfrac{dx}{(x^{2}+4)^{2}} &=& \dfrac{1}{16}(\theta +\sin \theta \cos \theta )\underset{\underset{\color{#0066A7}{\hbox{\(x=2\tan \theta{;} \theta =\tan^{-1}\dfrac{x}{2}\)}}}{\color{#0066A7}{\uparrow}}}{=} \dfrac{1}{16}\left( \tan ^{-1}\dfrac{x}{2}+\dfrac{2x}{x^{2}+4}\right)\tag{6} \end{eqnarray*}$$

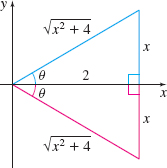
Now use the results of (3), (4), (5), and (6): $$\int \dfrac{x^{3}+1}{(x^{2}+4)^{2}}dx=\dfrac{1}{2}\ln (x^{2}+4)+\dfrac{2}{ x^{2}+4}+\dfrac{1}{16}\tan ^{-1}\dfrac{x}{2}+\dfrac{x}{8(x^{2}+4)}+C_{1}$$

NOW WORK

Problem 23.