Chapter 9

Section 9.1

1. Plane curve; parameter

2. (c)

3. (d)

4. Cycloid

5. False

6. True

7. (a) x = 2y − 3

(b)

9. (a) x = 2y−3, 1 ≤ x ≤ 5

(b)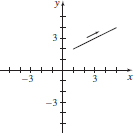

11. (a) x = ey

(b)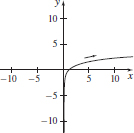

13. (a) x2 + y2 = 1

(b)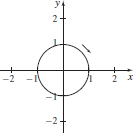

15. (a)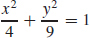

(b)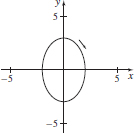

17. (a)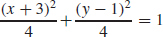

(b)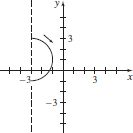

19. (a) x = 3

(b)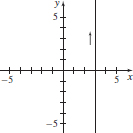

21. (a) x = 2

(b)

(c) x = 2, y = 4

(d)

23. (a) x = y2 + 5

(b)

(c) x ≥ 5, y ≥ 0

(d)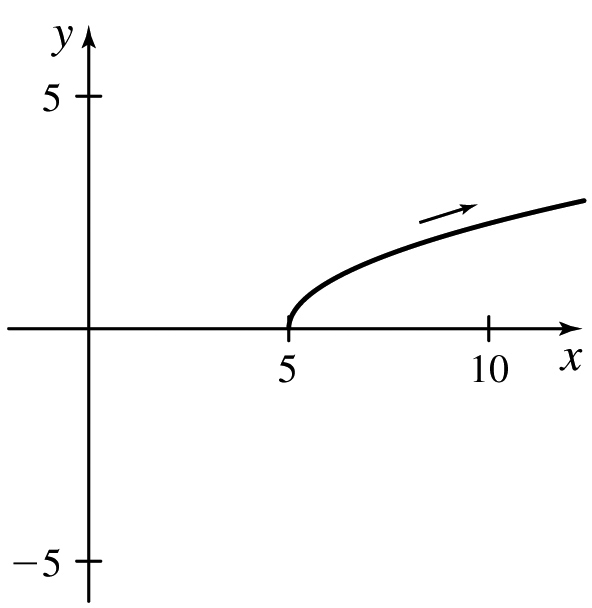

25. (a) y = (x − 1)3

(b)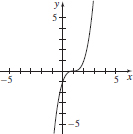

(c) x ≥ 2, y ≥ 1

(d)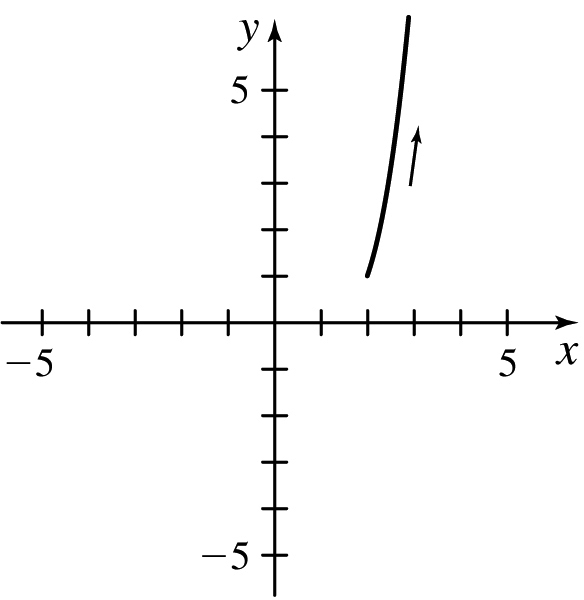

27. (a) x = sec tan-1 y

(b)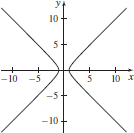

(c) x ≥ 1

(d)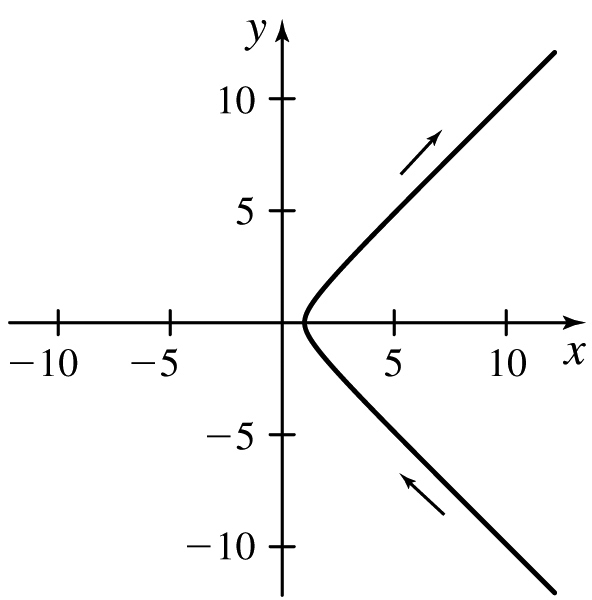

29. (a) x = y2

(b)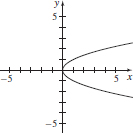

(c) x ≥ 0, y ≥ 0

(d)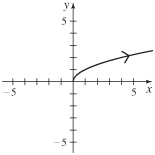

31. (a) x =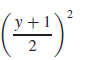

(b)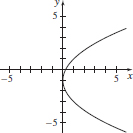

(c) x ≥ 0

(d)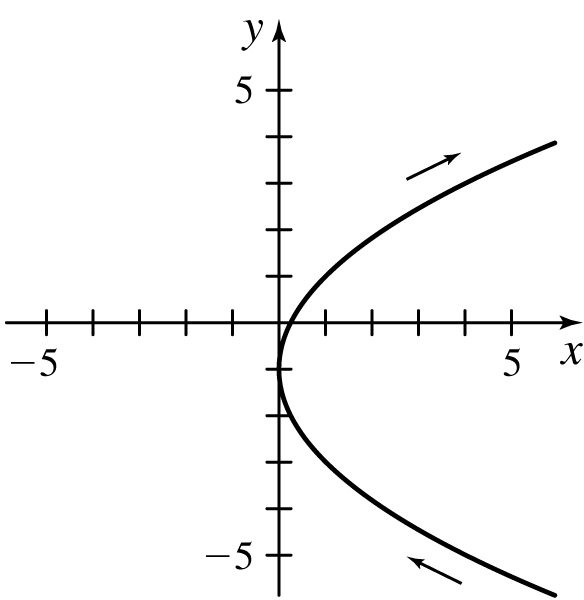

33. (a) x =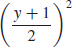

(b)

(c) x > 0, y ≠ -1

(d)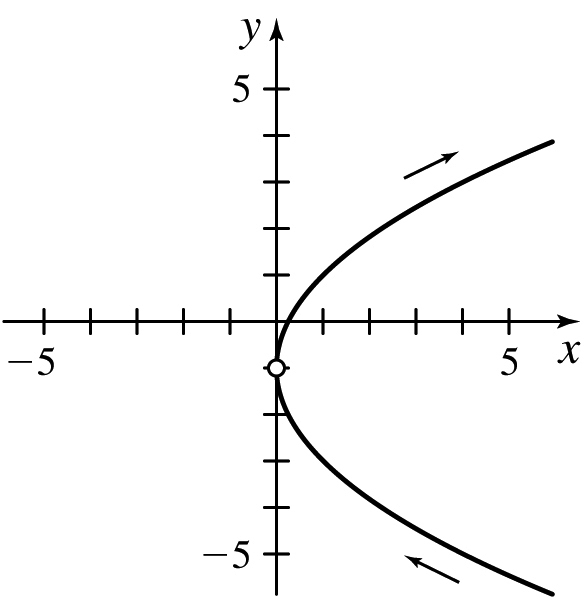

35. (a)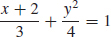

(b)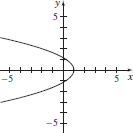

(c) −2 ≤ x ≤ 1, −2 ≤ y ≤ 2

(d)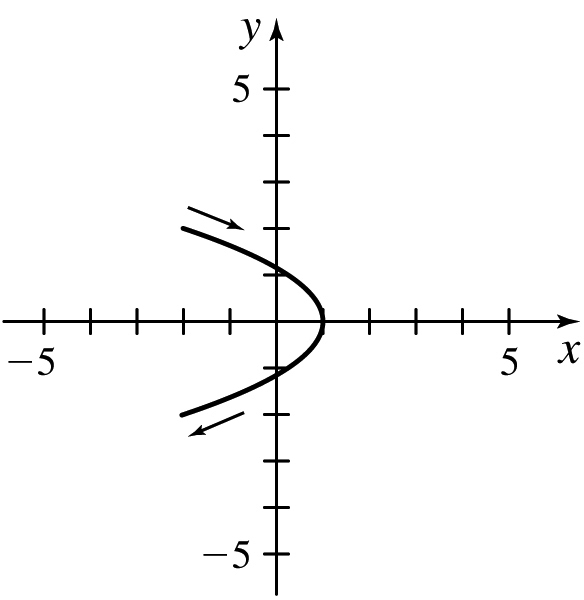

37. y = 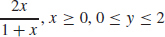Answers will vary.

39. \(y = 2\sqrt{x^{2} - 4}\). Answers will vary.

41.

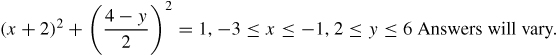
43. Answers will vary.

45. Answers will vary.

47. Answers will vary.

49. Answers will vary.

51. Answers will vary.

53. Answers will vary.

55. 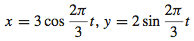, 0 ≤ t ≤ 3

57. x = 3 sin (πt), y = 2 cos (πt), 0 ≤ t ≤ 2

59. (a)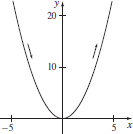

(b)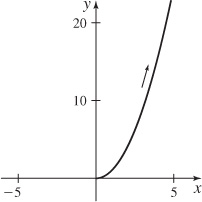

(c)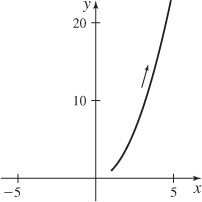

(d)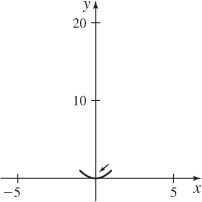

61. \(I\rightarrow(d)\;\text{counterclockwise}\), \(II\rightarrow(a)\;\text{counterclockwise}\), \(III\rightarrow(b)\;\text{counterclockwise}\), \(IV\rightarrow(c)\;\text{counterclockwise}\)

63. I → (c) from (1, 0) to (−1, 0), I I → (b) from (−1, 0) to (1, 0), I I I → (a) clockwise, I V → (d) from 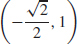to (1,0)

65. (a)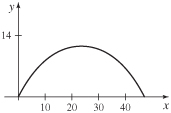

(b) x ≈ 8.66, y ≈ 10.53

67. Answers will vary.

69. (a) x(t) = (125 cos 40°)t, y(t) = −16t2 + (125 sin 40°)t + 3

(b) y ≈ 99.6 ft

(c) x ≈ 191.5 ft

(d) t ≈ 3.13 s

(e) y ≈ 97.7 ft

(f) t ≈ 5.06 s

(g) x ≈ 484.5 ft

71. (a) x(t) = (80 cos 35°)t, y(t) = −16t2 + (80 sin 35°)t + 6

(b) y ≈ 35.9 ft

(c) x ≈ 65.5 ft

(d) t ≈ 1.83 s

(e) y ≈ 36.4 ft

73. The first curve is counterclockwise from (2, 0); the second is clockwise from (0, 2). Answers will vary.

75.

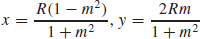
77. See Student Solutions Manual.

79.

Section 9.2

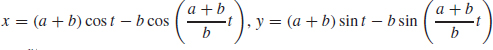
1. (a)

2. True

3. Horizontal; vertical

4. False

5.

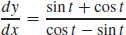
7.

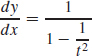
9.

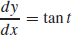
11.

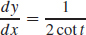
13. (a) y =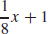

(b)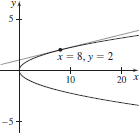

15. (a) y =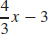

(b)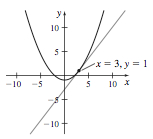

17. (a) y =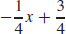

(b)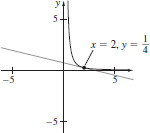

19. (a) y = −2x + 2

(b)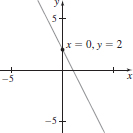

21. (a) y = −x + 2

(b)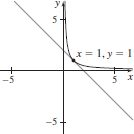

23. (a) y = −x +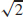

(b)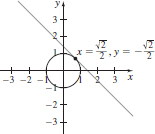

25. (a) y =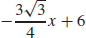

(b)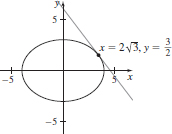

27. Horizontal at 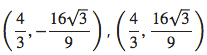; vertical at (0, 0)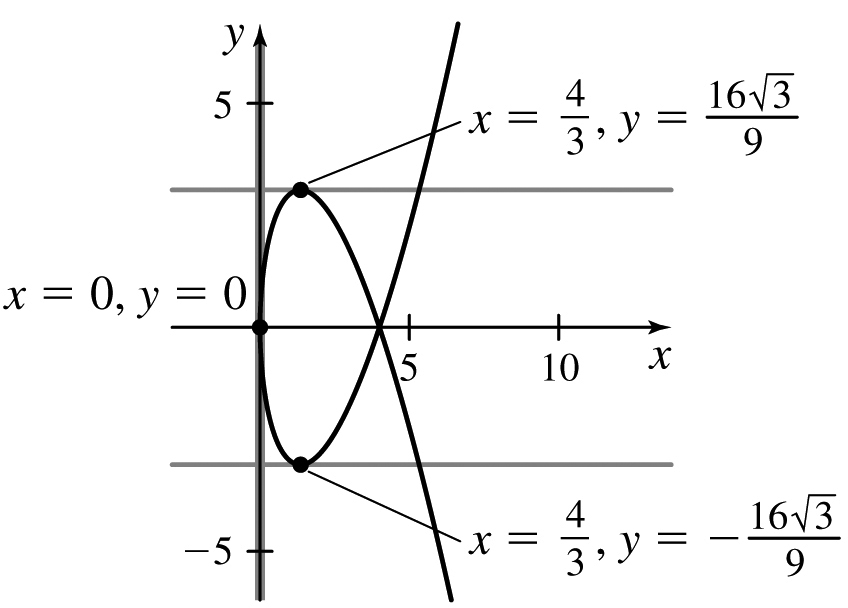

29. Horizontal at (1, 0), (1, 2); vertical at (0, 1), (2, 1)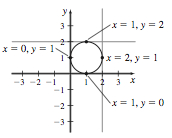

31.

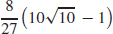
33.

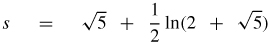
35. 4π

37. 4π

39. (a) s =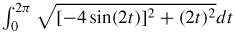

(b) s ≈ 44.527

(c)

41. (a) s =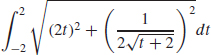

(b) s ≈ 8.429

(c)

43. (a) s = 4 ·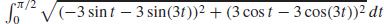

(b) s = 24

(c)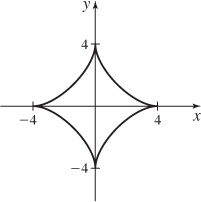

45. (a) Horizontal at 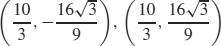; vertical at (2, 0)

(b) t = 2, t = −2; see Student Solutions Manual

(c) y = 2x − 12, y = −2x + 12

(d)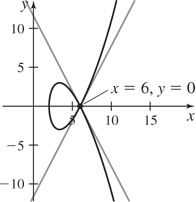

47. (a) s =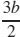

(b) b = 1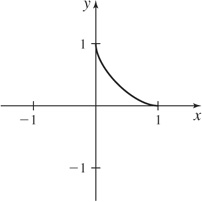

49.

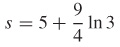
51.

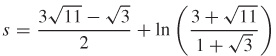
53.

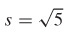
55.

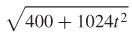
57.

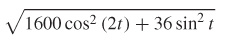
59. See Student Solutions Manual.

61. 0.73423

63.

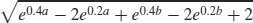
65.

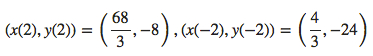
67.

Section 9.3

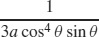
1. False

2. s =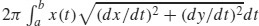

3.

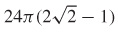
5.

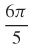
7.

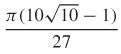
9.

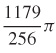
11.

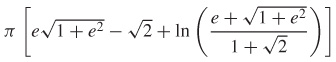
13. 4πa2

15.

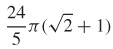
17. 8π

19.

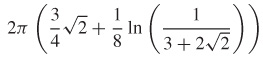
21. 768π

23. (a) Infinite

(b) π

25.

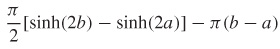
27. See Student Solutions Manual.

29.

Section 9.4

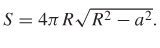
1. Pole, polar axis

2. False

3. False

4. True

5. True

6. True

7. x = r cos θ, y = r sin θ

8. Polar equation

9. A

11. C

13. B

15. A

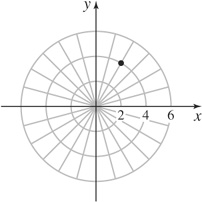
17.

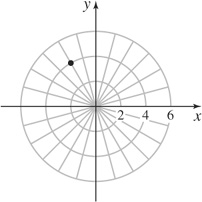
19.

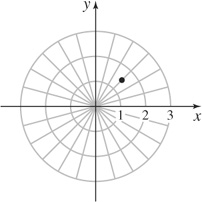
21.

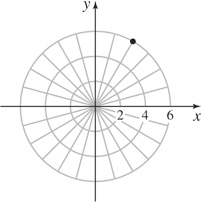
23.

25. (a)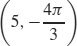

(b)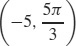

(c)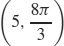

27. (a) (2, −2π)

(b) (−2, π)

(c) (2, 2π)

29. (a)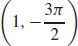

(b)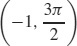

(c)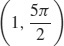

31. (a)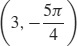

(b)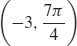

(c)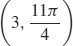

33.

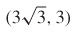
35.

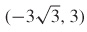
37. (0, 5)

39. (2, −2)

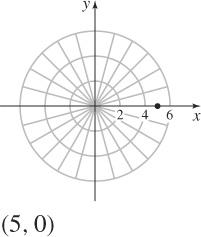
41.

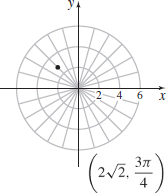
43.

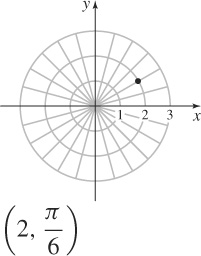
45.

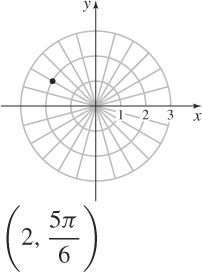
47.

49.

51. E

53. F

55. H

57. D

59. The circle centered at (0,0) of radius 4.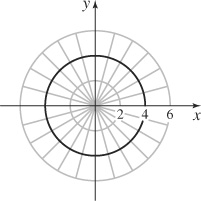

61. A line through the origin.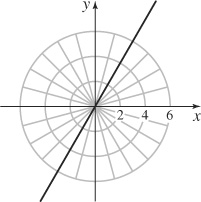

63. The line \(y=4\).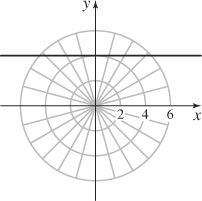

65. The line \(x = −2\).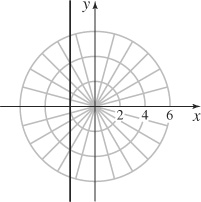

67. The circle centered at (1,0) of radius 1.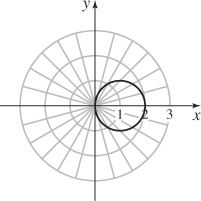

69. The circle centered at (0, −2) of radius 2.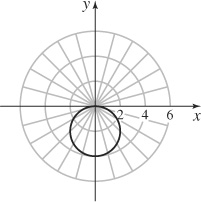

71. The circle centered at (2,0) of radius 2 excluding the pole.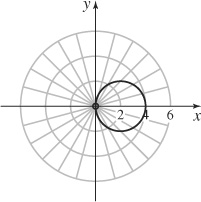

73. The circle centered at (0, −1) of radius 1, excluding the pole.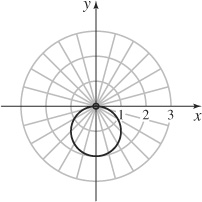

75. r =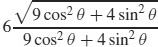

77. r = 4 cos θ

79. r2 cos2 θ + 4r sin θ − 1 = 0

81. r =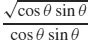

83.

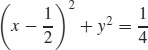
85. y =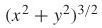

87. 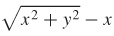= 4

89. y = x tan(x2 + y2)

91. y =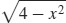

93. y = 4x

95. (a) x = −10, y = 36

(b) (37.363, 1.842)

(c) x = −3, y = −35

(d) (35.128, 4.627)

97. See Student Solutions Manual

99. See Student Solutions Manual

101. See Student Solutions Manual

103. (a)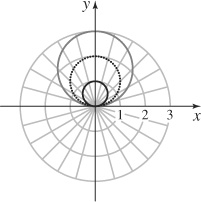

(b) Answers will vary.

(c)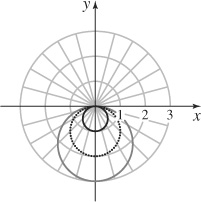

(d) Answers will vary.

105. See Student Solutions Manual.

107. See Student Solutions Manual.

Section 9.5

1. True

2. a, c, b

3. True

4. 3

5. (a)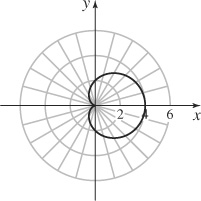

(b)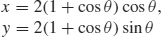

7. (a)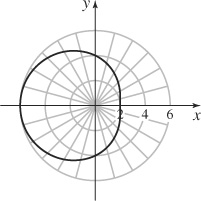

(b)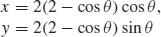

9. (a)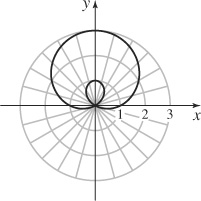

(b)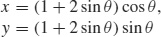

11. (a)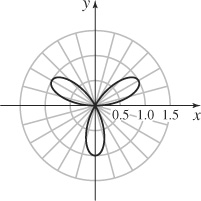

(b)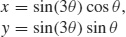

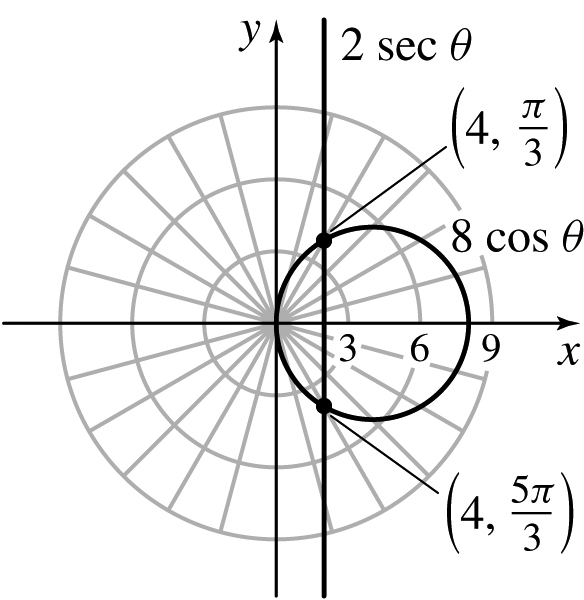
13.

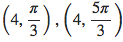
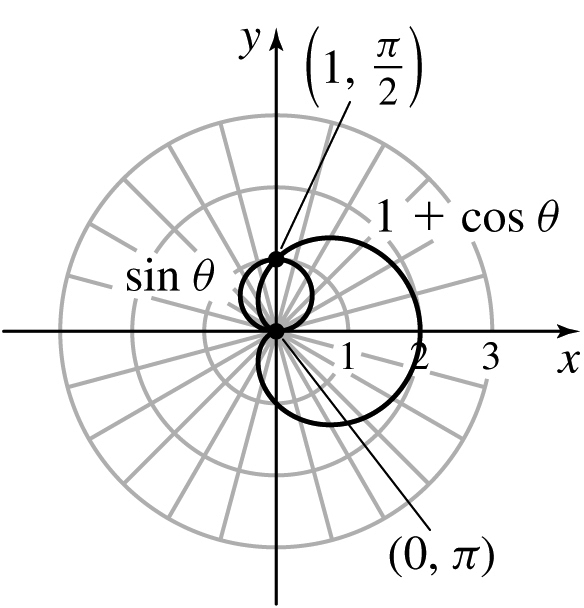
15.

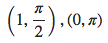
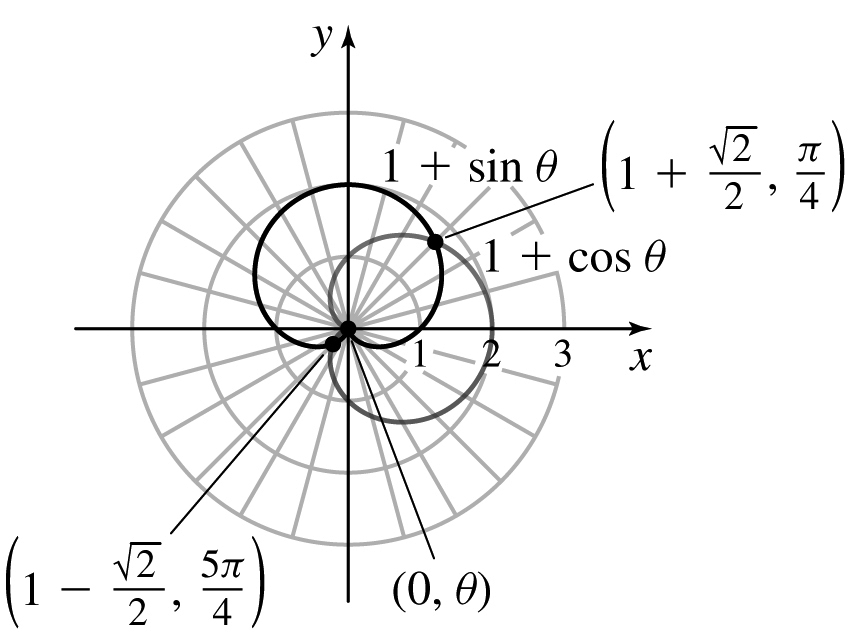
17.

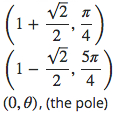
19.

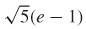
21. 2

23. 3 + 3 cos θ

25. 4 + sin θ

27. y =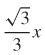

29. y =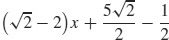

31. y =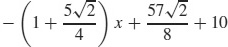

33. (a)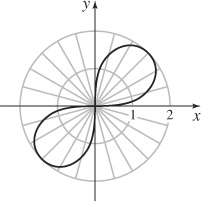

(b)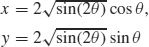

35. (a)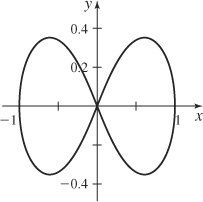

(b)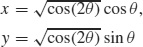

37. (a)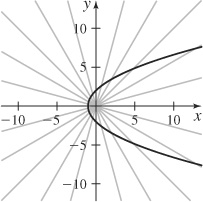

(b)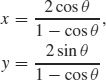

39. (a)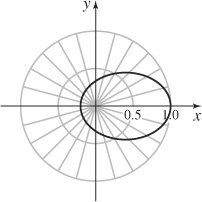

(b)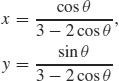

41. (a)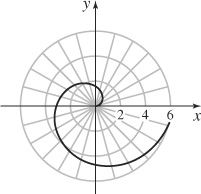

(b)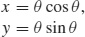

43. (a)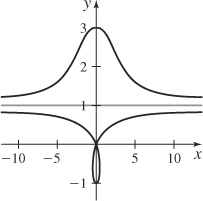

(b) ,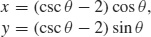

45. (a)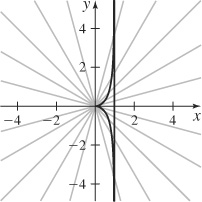

(b)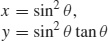

47. (a)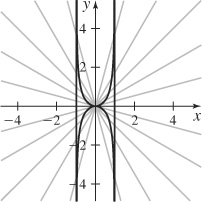

(b)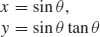

49. See Student Solutions Manual.

51. \(\pi\sqrt{1+4\pi^{2}}+\dfrac{1}{2}\ln(2\pi + \sqrt{4\pi^{2} + 1}) \)

53. 8

55. Answers will vary.

57. Horizontal: 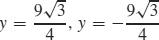vertical: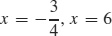

59. Horizontal: 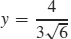, , 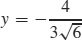y = 2, y = −2; vertical: 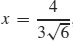, , x = 2, x = −2

61. Horizontal: 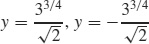; vertical: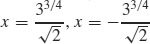

63. (a) Answers will vary.

(b) See Student Solutions Manual.

65. See Student Solutions Manual.

67. (a)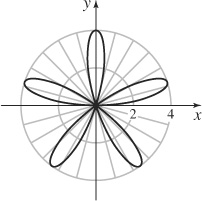

(b)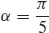

(c) ≈ 8.404

Section 9.6

1.

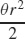
2. True

3. False

4. True

5.

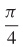
7.

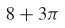
9.

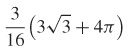
11.

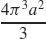
13.

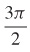
15.

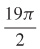
17. 16π

19. 2π

21. 2

23.

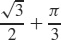
25.

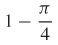
27.

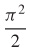
29.

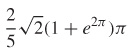
31.

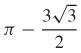
33.

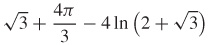
35.

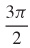
37.

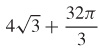
39.

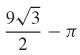
41.

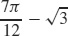
43.

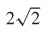
45.

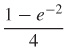
47.

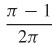
49.

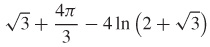
51. (a)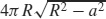

(b) Answers will vary

53.

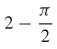
55. See Student Solutions Manual.

57.

Section 9.7

1. (a)

2. Answers will vary.

3. Answers will vary.

4. False

5. A parabola, e = 1, directrix perpendicular to the polar axis p = 1 units to the right of the pole

7. A hyperbola, e = 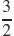, directrix parallel to the polar axis p = 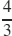units below the pole

9. An ellipse, e = , directrix perpendicular to the polar axis p = 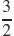units to the left of the pole

11. A parabola, e = 1, directrix parallel to the polar axis p = 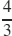units above the pole

13. (a) Ellipse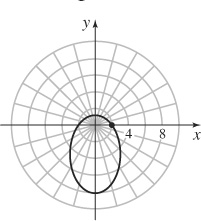

(b)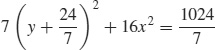

(c)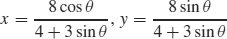

15. (a) Hyperbola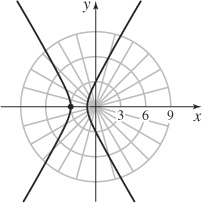

(b) 3(x + 2)2 − y2 = 3

(c)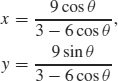

17. (a) Ellipse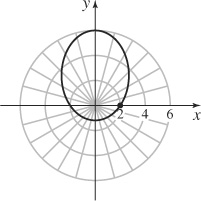

(b)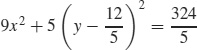

(c)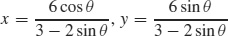

19. (a) Ellipse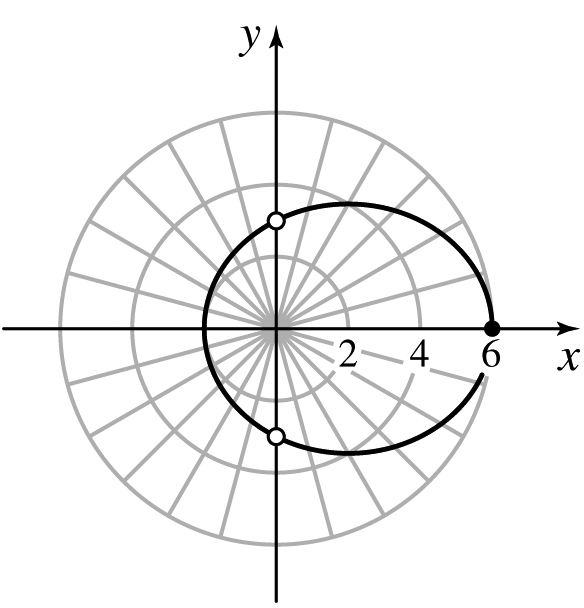

(b) 4y2 + 3(x − 2)2 = 48

(c)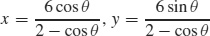

21. undefined

23. 0

25. undefined

27. r =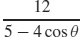

29. r =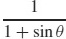

31. r =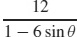

33. (a) 0.967

(b) 0.587 AU

(c) 35 AU

(d)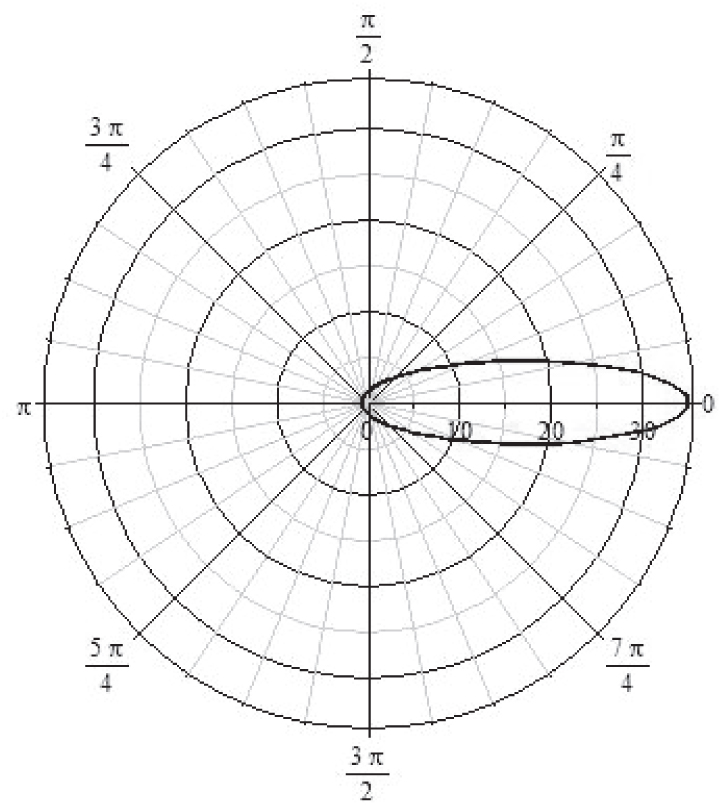

35. (a) See Student Solutions Manual.

(b) Answers will vary.

(c) Answers will vary.

37. See Student Solutions Manual.

39. See Student Solutions Manual.

Review Exercises

1. (a) x = −4y + 2

(b)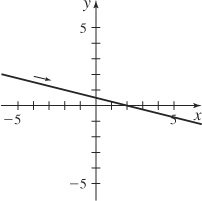

(c) No restrictions

3. (a) y =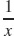

(b)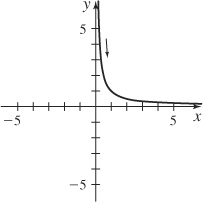

(c) x ≥ 0, y ≥ 0

5. (a) y + 1 = x

(b)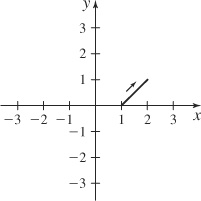

(c) 1 ≤ x ≤ 2, 0 ≤ y ≤ 1

7. (a) y =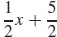

(b)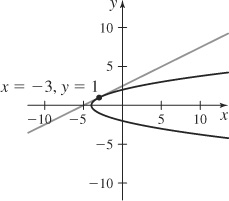

9. (a) y =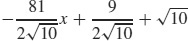

(b)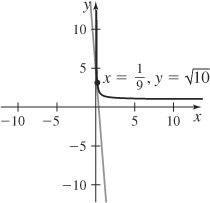

11. Answers will vary.

13.

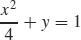
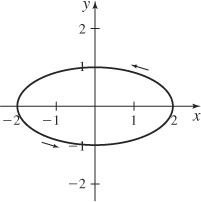
15.

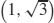
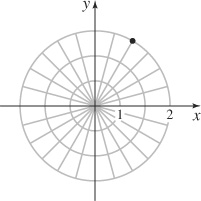
17.

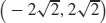
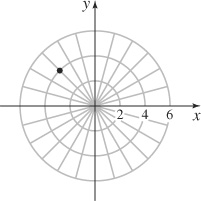
19. (5, 0.927), (−5, 4.068)

21.

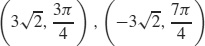
23. y = x tan ln(x2 + y2)

25.

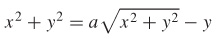
27. y =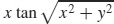

29. cos2 θ − sin2 θ = r2, r ≠ 0

31. r =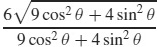

33. The circle centered at (1,0) of radius 1.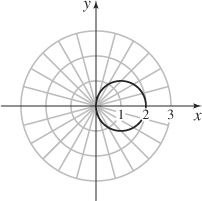

35.

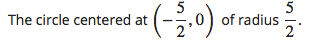
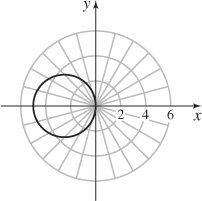
37. (a)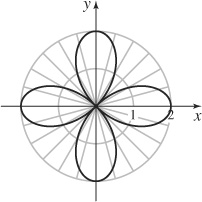

(b) x = 4 cos(2θ) cos θ , y = 4 cos(2θ) sin θ

39. (a)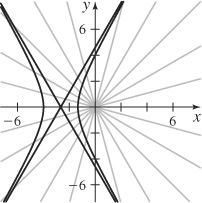

(b)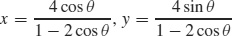

41. (a)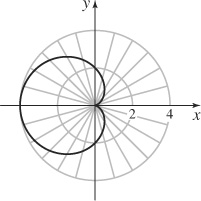

(b)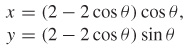

43. (a)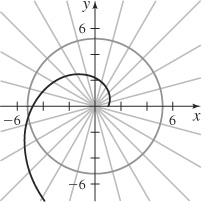

(b)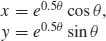

45. (a)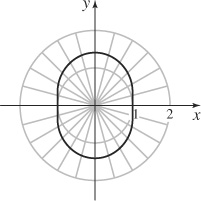

(b)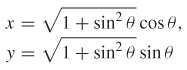

47. (a) An ellipse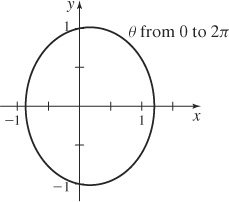



(b)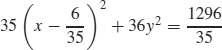

(c)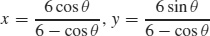

49.

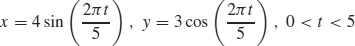
51. Vertical: (0, 2), (2, 2); horizontal: (1, 5), (1,−1)

53. \(s=\dfrac{1}{3}\dfrac{\sqrt{13}}{2}+\dfrac{9}{8}\ln\left(1+\dfrac{\sqrt{13}}{2}\right)-\dfrac{9}{8}\ln\left(\dfrac{\sqrt{13}}{2}\right)\)

55. \(s=\dfrac{3}{2}+\dfrac{1}{4}\ln2\)

57.

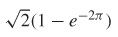
59.

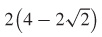
61.

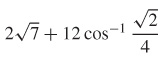
63.

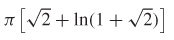
65.

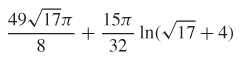
67. 16π