Chapter 1
Section 1.1
1. (c)
2. True
3. False
4. False
5. slope
6. False
7. 
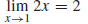
9. 
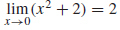
11. 
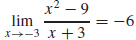
13. 
15. 
17. (a) 2
(b) 2
(c) 2
19. (a) 3
(b) 6
(c) The limit does not exist.
21. 1
23. 1
25. The limit does not exist because the two one-sided limits are not equal.
27. The limit does not exist because the two one-sided limits are not equal.
29. 9
31. The limit does not exist.
33. 2
35. The limit does not exist.
37. Answers will vary.
39. Answers will vary.
41. 1
43. 0
45. 1
47. 0
49. 0
51. (a) msec = 15
(b) msec = 3(x + 2)
(c)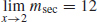 
(d) 
53. (a) msec = 2 +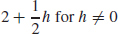 
(b)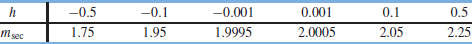 
(c)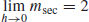 
(d) mtan = 2
(e)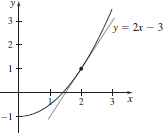 
55. (a) These values suggest that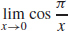 
= 1.
(b) These values suggest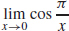 
= −1
(c)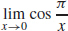 
does not exist. Answers will vary.
(d) Answers will vary.
57. (a) The table suggests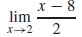 
= −3
(b) 1.8 ≤ x ≤ 2.2
(c) 1.98 ≤ x ≤ 2.02
59. (a) C(w) =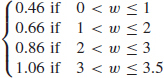 
(b) {w|0 < w ≤ 3.5}
(c) See the graph below.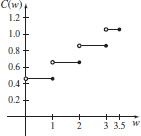 
(d) The graph suggests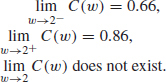 
(e) The graph suggests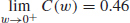 
(f) The graph suggests 
61. (a) 
(b) Given any 
> 0, there is a number δ > 0 so that whenever 0 < |t − 7| < δ then |S(t) − 100| <
.
63. Answers will vary.
65. (a) The graph of f (x) is the horizontal line y = −1 excluding the point (3,−1).
(b)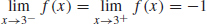 
(c) The graph suggests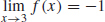 
f (x) = −1.
67. 0
69. 0
Section 1.2
1. (a) −3
(b) π
2. 243
3. 4
4. (a) −1
(b) e
5. (a) −2
(b) 
6. (a) −6
(b) 0
7. True
8. 2
9. False
10. True
11. 14
13. 0
15. 1
17. 6
19. 
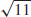
21. 
23. 
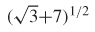
25. 0
27. 5
29. 
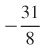
31. 10
33. 
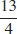
35. 4
37. 2
39. 2
41. 
43. 
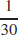
45. 5
47. 6
49. 9
51. −1
53. 8
55. 0
57. 
59. (a) 6
(b) −16
(c) −16
(d) 0
(e) 
.
(f) 0
61. 6
63. −4
65. 
67. 4
69. 6x + 4
71. 
73. 
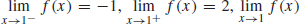does not exist
75. 
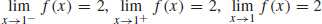
77. 
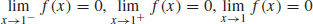
79. 
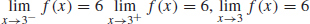
81. The limit does not exist.
83. 2x
85. 
87. 
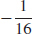
89. 6
91. 0
93.
(a) \(C(x)={\left\{ \begin{array}{ll}
9.00 & \hbox{if} & 0 \leq x \leq 10 \\
9.00 + 0.95(x-10) & \hbox{if} & 10 \lt x \leq30 \\
28.00 + 1.65(x-30) & \hbox{if} & 30 \lt x \leq 100 \\
143.50 + 2.20(x-100) & \hbox{if} & x \gt 100
\end{array} \right. }\)
(b) {x|x ≥ 0}
(c) \(\mathop {\lim\limits_{x \to 5}} C(x) = 9.00\), \(\mathop {\lim\limits_{x \to 10}} C(x) = 9.00\), \(\mathop {\lim\limits_{x \to 30}} C(x) = 28.00\), \(\mathop {\lim\limits_{x \to 100}} C(x) = 143.50\)
(d) 9.00
(e)
95. (a) 0
(b) Answers will vary.
97. See Student Solutions Manual.
99. Answers will vary.
101. Answers will vary.
103. See Student Solution Manual.
105. nan−1
107. 
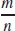
109. 
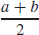
111. 0.
Section 1.3
1. True
2. False
3. f (c) is defined, 
exists, 
4. True
5. False.
6. False
7. False
8. True
9. The function is discontinuous.
10. The function is continuous.
11. True
12. False
13. (a) The function is not continuous at c = −3.
(b) 
(c) The discontinuity is removable.
(d) f (−3) = −2
15. (a) The function is not continuous at c = 2.
(b)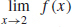 
does not exist.
(c) The discontinuity is not removable.
17. (a) The function is continuous at c = 4.
19. The function is continuous at c = −1.
21. The function is continuous at c = −2.
23. The function is continuous at c = 2.
25. The function is not continuous at c = 1.
27. The function is not continuous at c = 1.
29. The function is continuous at c = 0.
31. The function is not continuous at c = 0.
33. f (2) = 4
35. f (1) = 2
37. The function is continuous on the given interval.
39. The function is not continuous on the given interval.
41. The function is continuous on {x|x ≠ 0}.
43. The function is continuous on the set of all real numbers.
45. The function is continuous on {x|x ≥ 0, x ≠ 9}.
47. The function is continuous on the set {x|x < 2}.
49. The function is continuous on the set of all real numbers.
51. f is continuous at 0 because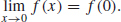 
53. f is not continuous at 3 because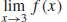 
does not exist.
55. f is continuous at 1 because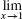 
f (x) = f (1).
57. (a) 
(b) Based on the graph, it appears that the function is continuous for all real numbers.
(c) f is actually continuous at all real numbers except x = 2.
(d) Answers will vary.
59. Yes. A zero exists on the given interval.
61. The IVT gives no information.
63. The IVT gives no information.
65. 1.154
67. 0.211
69. 3.134
71. 1.157
73. (a) Since f is continuous on [0, 1], f (0) < 0, and f (1) = 0, the IVT guarantees that f must have a zero on the interval (0, 1).
(b) 0.828
75. The function is not continuous at c = 1.
77. The function is continuous on the set of all real numbers.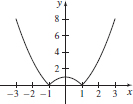
79. (a) C(w) =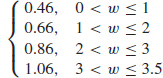 
(b) {w|0 < w ≤ 3.5}
(c) The function is continuous on the intervals (0, 1], (1, 2], (2, 3], and (3, 3.5].
(d) At w = 1, w = 2, and w = 3, the function has a jump discontinuity.
(e) Answers will vary.
81. (a) C(x) =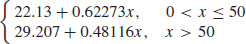 
(b) {x|x = 0}
(c) C(x) is continuous on its domain.
(d) See (c).
(e) Answers will vary.
83. (a)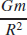 
(b) 1.3 m/s2
(c) Answers will vary.
85. A = 5, B = 7
87. (a) {x|x < 2} 
{x|x = 2, x = 8}
(b) f is discontinuous at x = 8.
(c) The discontinuity at x = 8 is removable.
89. (a) Since f is continuous on [0, 2], f (0) < 0 and f (2) = 0, the IVT guarantees that f must have a zero on the interval (0, 2).
(b) x ≈ 0.443
91. This does not contradict the IVT. Answers will vary.
93. This does not contradict the IVT. Answers will vary.
95. (a) Answers will vary.
(b) The graph below indicates that f does not have a zero in the interval (−2, 2).
97. Answers will vary.
99. (a) x = −2, x = 2, x = 3
(b) p = 5
(c) h(x) is an even function.
101. Answers will vary.
103. 1.1875
105. 0.1875
107. 3.1875
109. 1.1875
111. Since f is continuous on [0, 1], f (0) < 0, and f (1) = 0, the IVT guarantees that f must have a zero on the interval (0, 1). Correct to one decimal place, the zero is x = 0.8
113. See Student Solution Manual.
115. See Student Solution Manual.
117. See Student Solution Manual.
119. See Student Solution Manual.
Section 1.4
1. 0
2. False
3. L
4. False
5. 1
7. 1
9. 0
11. 
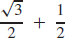
13. 1
15. 
17. 0
19. 1
21. 
23. 7
25. 2
27.
29. 5
31. 0
33. 1
35. f is continuous at c = 0.
37. f is continuous at c = 
.
39. f is continuous on {x|x ≠ 4}.
41. f is continuous on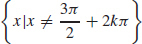 
, k an integer.
43. f is continuous on {x|x = 0, x ≠ 3}.
45. f is continuous on the set of all real numbers.
47. 0
49. 0
51. See Student Solution Manual.
53. See Student Solution Manual.
55. (a)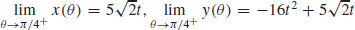 
(b) Answers will vary.
(c) 
(d) Answers will vary.
57. See Student Solution Manual.
59. f (0) = π
61. Yes
63. See Student Solution Manual.
65. See Student Solution Manual.
67. Answers will vary.
69. 0
71. 
Section 1.5
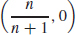
1. False
2. (a) −∞
(b) ∞
(c) −∞
3. False
4. vertical
5. (a) 0
(b) 0
(c) ∞
6. False
7. (a) 0
(b) ∞
(c) 0
8. True
9. 2
11. ∞
13. ∞
15. x = −1, x = 3
17. −3
19. ∞
21. 0
23. ∞
25. x = −3, x = 0, x = 4
27. −∞
29. ∞
31. ∞
33. ∞
35. −∞
37. −∞
39. −∞
41. −∞
43. 0
45. 
47. 1
49. 0
51. 
53. 0
55. 0
57. 
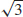
59. −∞
61. x = 0 is a vertical asymptote. y = 3 is a horizontal asymptote.
63. x = −1 and x = 1 are vertical asymptotes. y = 1 is a horizontal asymptote.
65. x = 
is a vertical asymptote. y =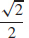 
and y = −
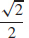are horizontal asymptotes.
67. (a) {x|x ≠ −2, x ≠ 0}
(b) y = 0 is a horizontal asymptote.
(c) x = 0 and x = −2 are vertical asymptotes.
(d) See Student Solution Manual.
69. (a)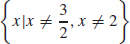 
(b) y = 
is a horizontal asymptote.
(c) x = 
is a vertical asymptote.
(d) See Student Solution Manual.
71. (a) {x|x ≠ 0, x ≠ 1}
(b) There are no horizontal asymptotes.
(c) x = 0 is a vertical asymptote.
(d) See Student Solution Manual.
73. Answers will vary.
75. (a) T
(b) u0
77. ∞
79. (a) 500
(b)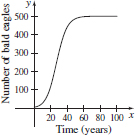 
(c) Answers will vary.
81. (a)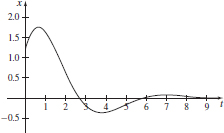 
The graph suggests that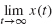 
= 0.
(b) 0
(c) Answers will vary.
83. (a) 0.26 moles
(b) 395 min
(c) 0 moles
(d) Answers will vary.
85. See Student Solution Manual.
87. See Student Solution Manual.
89. See Student Solution Manual.
91. (a)
(b) e ≈ 2.718281828
(c) Answers will vary.
93. (a) ∞
(b) Answers will vary.
Section 1.6
1. False
2. True
3. True
4. False
5. True
6. False
7. δ = 0.005
9. δ =
11. δ = 0.02
13. (a) δ ≤ 0.025
(b) δ ≤ 0.0025
(c) δ ≤ 0.00025
(d) δ ≤ 
15. (a) δ ≤ 0.1
(b) δ ≤ 0.01
(c) δ ≤
17. Given any
> 0, let δ ≤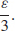 
See Student Solution Manual for the complete proof.
19. Given any
> 0, let δ ≤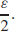 
See Student Solution Manual for the complete proof.
21. Given any
> 0, let δ ≤ 
See Student Solution Manual for the complete proof.
23. Given any
> 0, let δ ≤ min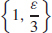 
. See Student Solution Manual for the complete proof.
25. Given any
> 0, let δ ≤ min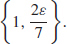 
See Student Solution Manual for the complete proof.
27. Given any
>, let δ ≤
3. See Student Solution Manual for the complete proof.
29. Given any
> 0, let δ ≤ min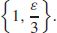 
See Student Solution Manual for the complete proof.
31. Given any
> 0, let δ ≤ min{1, 6
}. See Student Solution Manual for the complete proof.
33. See Student Solution Manual.
35. Given any
> 0, let δ ≤ min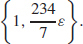 
See Student Solution Manual for the complete proof.
37. Given any
> 0, let δ ≤ min{1, 26
}. See Student Solution Manual for the complete proof.
39. Given any
> 0, let δ ≤ 
See Student Solution Manual for the complete proof.
41. x must be within 0.05 of 3.
43. See Student Solution Manual.
45. See Student Solution Manual.
47. See Student Solution Manual.
49. See Student Solution Manual.
51. See Student Solution Manual.
53. Given any
= 0, let δ ≤ min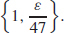
. See Student Solution Manual for the complete proof.
55. M = 101
57. See Student Solution Manual.
Review Exercises
1. The table suggests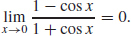 
3.
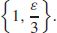f (x) does not exist.
5. 
7. 1
9. –π
11. 0
13. 27
15. 4
17. 
19. 
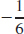
21. 6
23. 5
25. −1
27. 8
29. 
31. f is not continuous at c = 1.
33. f is continuous at c = 0.
35. f is not continuous at c = 1/2.
37. (a) 2x − 3
(b) −1
39. f is continuous on the set {x|x ≠ 3}.
41. f is continuous on the set {x|x ≠ −2, x ≠ 0}.
43. f is continuous on the set of all real numbers.
45. 0.215
47. 
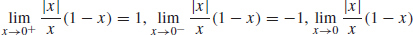does not exist.
49. 
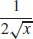
51. 1
53. 
55. 0
57. −∞
59. 3
61. x = −3 is a vertical asymptote. y = 4 is a horizontal asymptote.
63. Yes
65. f (0) = −π
67. (a) Answers will vary.
69. See Student Solution Manual.