The study of the rates of chemical reactions is called kinetics,and the study of the rates of enzyme-catalyzed reactions is called enzyme kinetics. A kinetic description of enzyme activity will help us understand how enzymes function. We begin by briefly examining some of the basic principles of reaction kinetics.

What do we mean when we say the “rate” of a chemical reaction? Consider a simple reaction:

The rate V is the quantity of A that disappears in a specified unit of time. It is equal to the rate of the appearance of P, or the quantity of P that appears in a specified unit of time.

If A is yellow and P is colorless, we can follow the decrease in the concentration of A by measuring the decrease in the intensity of yellow color with time. Consider only the change in the concentration of A for now. The rate of the reaction is directly related to the concentration of A by a proportionality constant, k, called the rate constant.

Reactions that are directly proportional to the reactant concentration are called first-order reactions. First-order rate constants have the units of s⁻¹.

Many important biochemical reactions include two reactants. For example,

or

226

They are called bimolecular reactions and the corresponding rate equations often take the form

and

The rate constants, called second-order rate constants, have the units M⁻¹ s⁻¹.

Sometimes, second-order reactions can appear to be first-order reactions. For instance, in reaction 11, if B is present in excess and A is present at low concentrations, the reaction rate will be first order with respect to A and will not appear to depend on the concentration of B. These reactions are called pseudo-first-order reactions, and we will see them a number of times in our study of biochemistry.

Interestingly enough, under some conditions, a reaction can be zero order. In these cases, the rate is independent of reactant concentrations. Enzyme-catalyzed reactions can approximate zero-order reactions under some circumstances.

The simplest way to investigate the reaction rate is to follow the increase in reaction product as a function of time. First, the extent of product formation is determined as a function of time for a series of substrate concentrations (Figure 8.10A). As expected, in each case, the amount of product formed increases with time, although eventually a time is reached when there is no net change in the concentration of S or P. The enzyme is still actively converting substrate into product and vice versa, but the reaction equilibrium has been attained. However, enzyme kinetics is more readily comprehended if we consider only the forward reaction. We can define the rate of catalysis V₀, or the initial rate of catalysis, as the number of moles of product formed per second when the reaction is just beginning—that is, when t ≈ 0 (Figure 8.10A). These experiments are repeated three to five times with each substrate concentration to insure the accuracy of and assess the variability of the values attained. Next, we plot V₀ versus the substrate concentration [S], assuming a constant amount of enzyme, showing the data points with error bars (Figure 8.10B). Finally, the data points are connected, yielding the results shown in Figure 8.10C. The rate of catalysis rises linearly as substrate concentration increases and then begins to level off and approach a maximum at higher substrate concentrations. For convenience, we will show idealized data without error bars, throughout the text, but it is important to keep in mind that in reality, all experiments are repeated multiple times.

In 1913, Leonor Michaelis and Maud Menten proposed a simple model to account for these kinetic characteristics. The critical feature in their treatment is that a specific ES complex is a necessary intermediate in catalysis. The model proposed is

An enzyme E combines with substrate S to form an ES complex, with a rate constant k₁. The ES complex has two possible fates. It can dissociate to E and S, with a rate constant k₋₁, or it can proceed to form product P, with a rate constant k₂. The ES complex can also be reformed from E and P by the reverse reaction with a rate constant k₋₂. However, as before, we can simplify these reactions by considering the rate of reaction at times close to zero (hence, V₀) when there is negligible product formation and thus no back reaction (k₋₂ [E][P] ≈ 0).

227

Thus, for the graph in Figure 8.11, V₀ is determined for each substrate concentration by measuring the rate of product formation at early times before P accumulates (Figure 8.10A).

We want an expression that relates the rate of catalysis to the concentrations of substrate and enzyme and the rates of the individual steps. Our starting point is that the catalytic rate is equal to the product of the concentration of the ES complex and k₂.

Now we need to express [ES] in terms of known quantities. The rates of formation and breakdown of ES are given by

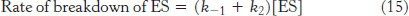
We will use the steady-state assumption to simplify matters. In a steady state, the concentrations of intermediates—in this case, [ES]—stay the same even if the concentrations of starting materials and products are changing. This steady state is reached when the rates of formation and breakdown of the ES complex are equal. Setting the right-hand sides of equations 14 and 15 equal gives

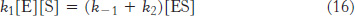
By rearranging equation 16, we obtain

Equation 17 can be simplified by defining a new constant, K_M, called the Michaelis constant:

Note that K_M has the units of concentration and is independent of enzyme and substrate concentrations. As will be explained, K_M is an important characteristic of enzyme–substrate interactions.

Inserting equation 18 into equation 17 and solving for [ES] yields

Now let us examine the numerator of equation 19. Because the substrate is usually present at a much higher concentration than that of the enzyme, the concentration of uncombined substrate [S] is very nearly equal to the total substrate concentration. The concentration of uncombined enzyme [E] is equal to the total enzyme concentration [E]_T minus the concentration of the ES complex:

Substituting this expression for [E] in equation 19 gives

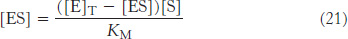
Solving equation 21 for [ES] gives

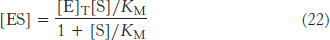
228

or

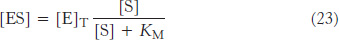
By substituting this expression for [ES] into equation 13, we obtain

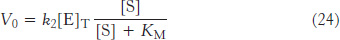
The maximal rate, V_max, is attained when the catalytic sites on the enzyme are saturated with substrate—that is, when [ES] = [E]_T. Thus,

Substituting equation 25 into equation 24 yields the Michaelis–Menten equation:

This equation accounts for the kinetic data given in Figure 8.11. At very low substrate concentration, when [S] is much less than K_M, V₀ = (V_max/K_M) [S]; that is, the reaction is first order with the rate directly proportional to the substrate concentration. At high substrate concentration, when [S] is much greater than K_M, V₀ = V_max; that is, the rate is maximal. The reaction is zero order, independent of substrate concentration.

The significance of K_M is clear when we set [S] = K_M in equation 26. When [S] = K_M, then V₀ = V_max/2. Thus, K_M is equal to the substrate concentration at which the reaction rate is half its maximal value. As we will see, K_M is an important characteristic of an enzyme-catalyzed reaction and is significant for its biological function.

The physiological consequence of K_M is illustrated by the sensitivity of some persons to ethanol. Such persons exhibit facial flushing and rapid heart rate (tachycardia) after ingesting even small amounts of alcohol. In the liver, alcohol dehydrogenase converts ethanol into acetaldehyde.

Normally, the acetaldehyde, which is the cause of the symptoms when present at high concentrations, is processed to acetate by aldehyde dehydrogenase.

Most people have two forms of the aldehyde dehydrogenase, a low K_M mitochondrial form and a high K_M cytoplasmic form. In susceptible persons, the mitochondrial enzyme is less active owing to the substitution of a single amino acid, and acetaldehyde is processed only by the cytoplasmic enzyme. Because this enzyme has a high K_M, it achieves a high rate of catalysis only at very high concentrations of acetaldehyde. Consequently, less acetaldehyde is converted into acetate; excess acetaldehyde escapes into the blood and accounts for the physiological effects.

K_M is equal to the substrate concentration that yields V_max/2; however V_max, like perfection, is only approached but never attained. How, then, can we experimentally determine K_M and V_max, and how do these parameters enhance our understanding of enzyme-catalyzed reactions? The Michaelis constant, K_M, and the maximal rate, V_max, can be readily derived from rates of catalysis measured at a variety of substrate concentrations if an enzyme operates according to the simple scheme given in equation 26. The derivation of K_M and V_max is most commonly achieved with the use of curve-fitting programs on a computer. However, an older method, although rarely used because the data points at high and low concentrations are weighted differently and thus sensitive to errors, is a source of further insight into the meaning of K_M and V_max.

229

Before the availability of computers, the determination of K_M and V_max values required algebraic manipulation of the Michaelis–Menten equation. The Michaelis–Menten equation is transformed into one that gives a straight-line plot that yields values for V_max and K_M. Taking the reciprocal of both sides of equation 26 gives

A plot of 1/V₀ versus 1/[S], called a Lineweaver–Burk or double-reciprocal plot, yields a straight line with a y-intercept of 1/V_max and a slope of K_M/V_max (Figure 8.12). The intercept on the x-axis is −1/K_M.

The K_M values of enzymes range widely (Table 8.4). For most enzymes, K_M lies between 10⁻¹ and 10⁻⁷ M. The K_M value for an enzyme depends on the particular substrate and on environmental conditions such as pH, temperature, and ionic strength. The Michaelis constant, K_M, as already noted, is equal to the concentration of substrate at which half the active sites are filled. Thus, K_M provides a measure of the substrate concentration required for significant catalysis to take place. For many enzymes, experimental evidence suggests that the K_M value provides an approximation of the substrate concentration in vivo, which in turn suggests that most enzymes evolved to have a K_M approximately equal to the substrate concentration commonly available. Why might it be beneficial to have a K_M value approximately equal to the commonly available substrate concentration? If the normal concentration of substrate is near K_M, the enzyme will display significant activity and yet the activity will be sensitive to changes in environmental conditions—that is, changes in substrate concentration. At values below K_M, enzymes are very sensitive to changes in substrate concentration but display little activity. At substrate values well above K_M, enzymes have great catalytic activity but are insensitive to changes in substrate concentration. Thus, with the normal substrate concentration being approximately K_M, the enzymes have significant activity (1/2 V_max) but are still sensitive to changes in substrate concentration.

Under certain circumstances, K_M reflects the strength of the enzyme–substrate interaction. In equation 18, K_M is defined as (k₋₁ + k₂)/k₁. Consider a case in which k₋₁ is much greater than k₂. Under such circumstances, the ES complex dissociates to E and S much more rapidly than product is formed. Under these conditions (k₋₁ ≫ k₂)

Equation 28 describes the dissociation constant of the ES complex.

230

In other words, K_M is equal to the dissociation constant of the ES complex if k₂ is much smaller than k₋₁. When this condition is met, K_M is a measure of the strength of the ES complex: a high K_M indicates weak binding; a low K_M indicates strong binding. It must be stressed that K_M indicates the affinity of the ES complex only when k₋₁ is much greater than k₂.

The maximal rate, V_max, reveals the turnover number of an enzyme, which is the number of substrate molecules converted into product by an enzyme molecule in a unit time when the enzyme is fully saturated with substrate. It is equal to the rate constant k₂, which is also called k_cat. The maximal rate, V_max, reveals the turnover number of an enzyme if the concentration of active sites [E]_T is known, because

and thus

For example, a 10⁻⁶ M solution of carbonic anhydrase catalyzes the formation of 0.6 M H₂CO₃ per second when the enzyme is fully saturated with substrate. Hence, k_cat is 6 × 10⁵ s⁻¹. This turnover number is one of the largest known. Each catalyzed reaction takes place in a time equal to, on average, 1/k_cat, which is 1.7 μs for carbonic anhydrase. The turnover numbers of most enzymes with their physiological substrates range from 1 to 10⁴ per second (Table 8.5).

K_M and V_max also permit the determination of f_ES, the fraction of active sites filled. This relation of f_ES to K_M and V_max is given by the following equation:

When the substrate concentration is much greater than K_M, the rate of catalysis is equal to V_max, which is a function of k_cat, the turnover number, as already described. However, most enzymes are not normally saturated with substrate. Under physiological conditions, the [S]/K_M ratio is typically between 0.01 and 1.0. When [S] ≪ K_M, the enzymatic rate is much less than k_cat because most of the active sites are unoccupied. Is there a number that characterizes the kinetics of an enzyme under these more typical cellular conditions? Indeed there is, as can be shown by combining equations 13 and 19 to give

When [S] ≪ K_M, the concentration of free enzyme [E], is nearly equal to the total concentration of enzyme [E]_T; so

Thus, when [S] ≪ K_M, the enzymatic velocity depends on the values of k_cat/K_M, [S], and [E]_T. Under these conditions, k_cat/K_M is the rate constant for the interaction of S and E. The rate constant k_cat/K_M, called the specificity constant, is a measure of catalytic efficiency because it takes into account both the rate of catalysis with a particular substrate (k_cat) and the nature of the enzyme–substrate interaction (K_M). For instance, by using k_cat/K_M values, we can compare an enzyme’s preference for different substrates. Table 8.6 shows the k_cat/K_M values for several different substrates of chymotrypsin. Chymotrypsin clearly has a preference for cleaving next to bulky, hydrophobic side chains.

231

How efficient can an enzyme be? We can approach this question by determining whether there are any physical limits on the value of k_cat/K_M. Note that the k_cat K_M ratio depends on k₁, k₋₁, and k_cat, as can be shown by substituting for K_M.

Suppose that the rate of formation of product (k_cat) is much faster than the rate of dissociation of the ES complex (k₋₁). The value of k_cat/K_M then approaches k₁. Thus, the ultimate limit on the value of k_cat/K_M is set by k₁, the rate of formation of the ES complex. This rate cannot be faster than the diffusion-controlled encounter of an enzyme and its substrate. Diffusion limits the value of k₁ and so it cannot be higher than between 10⁸ and 10⁹ s⁻¹ M⁻¹. Hence, the upper limit on k_cat/K_M is between 10⁸ and 10⁹ s⁻¹ M⁻¹.

The k_cat/K_M ratios of the enzymes superoxide dismutase, acetylcholinesterase, and triose phosphate isomerase are between 10⁸ and 10⁹ s⁻¹ M⁻¹. Enzymes that have k_cat/K_M ratios at the upper limits have attained kinetic perfection. Their catalytic velocity is restricted only by the rate at which they encounter substrate in the solution (Table 8.7). Any further gain in catalytic rate can come only by decreasing the time for diffusion of the substrate into the enzyme’s immediate environment. Remember that the active site is only a small part of the total enzyme structure. Yet, for catalytically perfect enzymes, every encounter between enzyme and substrate is productive. In these cases, there may be attractive electrostatic forces on the enzyme that entice the substrate to the active site. These forces are sometimes referred to poetically as Circe effects.

The diffusion of a substrate throughout a solution can also be partly overcome by confining substrates and products in the limited volume of a multienzyme complex. Indeed, some series of enzymes are organized into complexes so that the product of one enzyme is very rapidly found by the next enzyme. In effect, products are channeled from one enzyme to the next, much as in an assembly line.

Most reactions in biological systems start with two substrates and yield two products. They can be represented by the bisubstrate reaction:

Many such reactions transfer a functional group, such as a phosphoryl or an ammonium group, from one substrate to the other. Those that are oxidation–reduction reactions transfer electrons between substrates. Multiple substrate reactions can be divided into two classes: sequential reactions and double-displacement reactions.

232

Sequential Reactions. In sequential reactions, all substrates must bind to the enzyme before any product is released. Consequently, in a bisubstrate reaction, a ternary complex of the enzyme and both substrates forms. Sequential mechanisms are of two types: ordered, in which the substrates bind the enzyme in a defined sequence, and random.

Many enzymes that have NAD⁺ or NADH as a substrate exhibit the ordered sequential mechanism. Consider lactate dehydrogenase, an important enzyme in glucose metabolism (Section 16.1). This enzyme reduces pyruvate to lactate while oxidizing NADH to NAD⁺.

In the ordered sequential mechanism, the coenzyme always binds first and the lactate is always released first. This sequence can be represented by using a notation developed by W. Wallace Cleland:

The enzyme exists as a ternary complex consisting of, first, the enzyme and substrates and, after catalysis, the enzyme and products.

In the random sequential mechanism, the order of the addition of substrates and the release of products is random. An example of a random sequential reaction is the formation of phosphocreatine and ADP from creatine and ATP which is catalyzed by creatine kinase (Section 15.2).

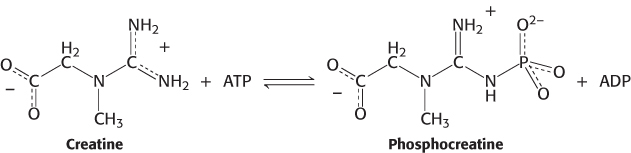
Either creatine or ATP may bind first, and either phosphocreatine or ADP may be released first. Phosphocreatine is an important energy source in muscle. Sequential random reactions also can be depicted in the Cleland notation.

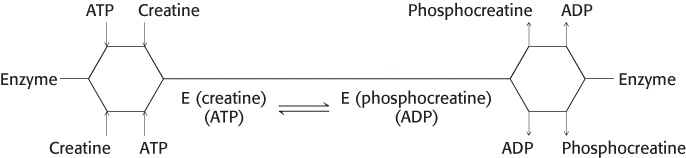
Although the order of certain events is random, the reaction still passes through the ternary complexes including, first, substrates and, then, products.

233

Double-displacement (ping-pong) reactions. In double-displacement, or ping-pong, reactions, one or more products are released before all substrates bind the enzyme. The defining feature of double-displacement reactions is the existence of a substituted enzyme intermediate, in which the enzyme is temporarily modified. Reactions that shuttle amino groups between amino acids and α-ketoacids are classic examples of double-displacement mechanisms. The enzyme aspartate aminotransferase catalyzes the transfer of an amino group from aspartate to α-ketoglutarate.

The sequence of events can be portrayed as the following Cleland notation:

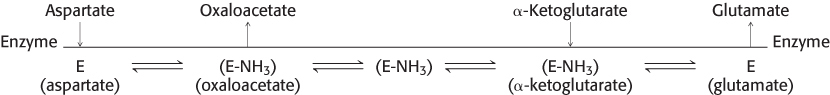
After aspartate binds to the enzyme, the enzyme accepts aspartate’s amino group to form the substituted enzyme intermediate. The first product, oxaloacetate, subsequently departs. The second substrate, α-ketoglutarate, binds to the enzyme, accepts the amino group from the modified enzyme, and is then released as the final product, glutamate. In the Cleland notation, the substrates appear to bounce on and off the enzyme much as a Ping-Pong ball bounces on a table.

The Michaelis–Menten model has greatly assisted the development of enzymology. Its virtues are simplicity and broad applicability. However, the Michaelis–Menten model cannot account for the kinetic properties of many enzymes. An important group of enzymes that do not obey Michaelis–Menten kinetics are the allosteric enzymes. These enzymes consist of multiple subunits and multiple active sites.

Allosteric enzymes often display sigmoidal plots of the reaction velocity V₀ versus substrate concentration [S] (Figure 8.13), rather than the hyperbolic plots predicted by the Michaelis–Menten equation (Figure 8.11). In allosteric enzymes, the binding of substrate to one active site can alter the properties of other active sites in the same enzyme molecule. A possible outcome of this interaction between subunits is that the binding of substrate becomes cooperative; that is, the binding of substrate to one active site facilitates the binding of substrate to the other active sites. Such cooperativity results in a sigmoidal plot of V₀ versus [S]. In addition, the activity of an allosteric enzyme may be altered by regulatory molecules that reversibly bind to specific sites other than the catalytic sites. The catalytic properties of allosteric enzymes can thus be adjusted to meet the immediate needs of a cell. For this reason, allosteric enzymes are key regulators of metabolic pathways (Chapter 10). Recall that we have already met an allosteric protein, hemoglobin, in Chapter 7.

234