Chapter 12
One-
289
Using the F Distributions with Three or More Samples
- Type I Errors When Making Three or More Comparisons
- The F Statistic as an Expansion of the z and t Statistics
- The F Distributions for Analyzing Variability to Compare Means
- The F Table
- The Language and Assumptions for ANOVA
One-
- Everything About ANOVA but the Calculations
- The Logic and Calculations of the F Statistic
- Making a Decision
Beyond Hypothesis Testing for the One-
- R2, the Effect Size for ANOVA
- Post Hoc Tests
- Tukey HSD
Next Steps: The Bonferroni Test
BEFORE YOU GO ON
- You should understand the z distribution and the t distributions. You should also be able to differentiate among distributions of scores (Chapter 6), means (Chapter 6), mean differences (Chapter 10), and differences between means (Chapter 11).
- You should know the six steps of hypothesis testing (Chapter 7).
- You should understand what variance is (Chapter 4).
- You should be able to differentiate between between-
groups designs and within- groups designs (Chapter 1). - You should understand the concept of effect size (Chapter 8).
290
In 1986, California created a task force to promote self-
In one experiment, researchers (Forsyth, Lawrence, Burnette, & Baumeister, 2007) randomly assigned university students who had earned D’s and F’s on their midterm exam to one of three groups. They received regular emails that provided them with (1) review questions (the control group); (2) review questions plus self-
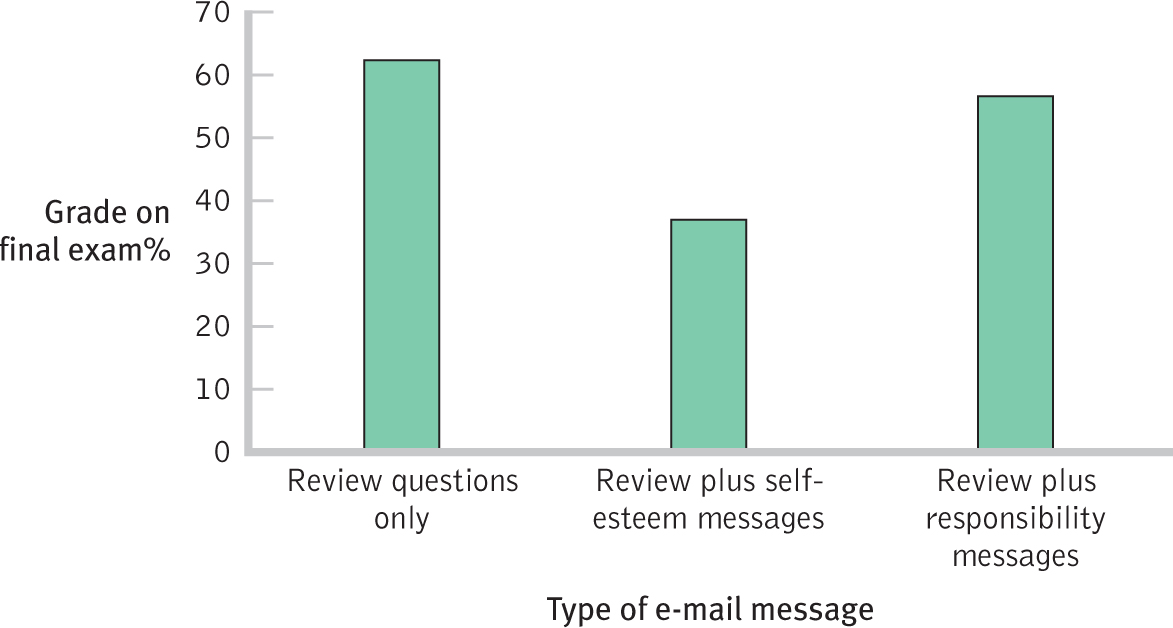
Figure 12-
For researchers, a three-