10.5 The Cross ProductPrinted Page 724
OBJECTIVES
When you finish this section, you should be able to:
The cross product of two vectors, defined only for vectors in space, is a third type of vector multiplication. It is of special interest for those studying physics, particularly mechanics and electricity, since it is used to describe angular velocity, torque, and angular momentum.
725
DEFINITION Cross Product
If v=v1i+v2j+v3k and w=w1i+w2j+w3k are two vectors in space, the cross product v×w is defined as the vector \bbox[5px, border:1px solid black, #F9F7ED]{ \mathbf{v}\times \mathbf{w}=(v_{2}w_{3}-v_{3}w_{2})\mathbf{i}-(v_{1}w_{3}-v_{3}w_{1})\,\mathbf{j}+(v_{1}w_{2}-v_{2}w_{1}) \mathbf{k} }
Because the cross product \mathbf{v}\times \mathbf{w} of two vectors is a vector, it is sometimes referred to as the vector product.
1 Find the Cross Product of Two VectorsPrinted Page 725
EXAMPLE 1Finding the Cross Product of Two Vectors
If \mathbf{v}=2\mathbf{i}-\mathbf{j}+\mathbf{k} and \mathbf{w}=4\mathbf{i} +2\mathbf{j}-\mathbf{k}, then using the definition of the cross product, we get \begin{eqnarray*} \mathbf{v}\times \mathbf{w}&=&[(-1)(-1)-(1)(2)]\mathbf{i}-[(2)(-1)-(1)(4)] \mathbf{j}+[(2)(2)-(-1)(4)]\mathbf{k}\\[4pt] &=&-\mathbf{i}+6\mathbf{j}+8\mathbf{k} \end{eqnarray*}
NOW WORK
Determinants are helpful for finding a cross product. A 2 by 2 determinant is a number or expression associated with an array containing two rows and two columns and is denoted by \begin{equation*} \left\vert \begin{array}{l@{\quad}l} a & b \\[3pt] c & d \end{array} \right\vert =ad-bc \end{equation*}
A 3 by 3 determinant is a number or expression associated with an array containing three rows and three columns. Its value is given by \begin{eqnarray*} \left\vert \begin{array}{l@{\quad}l@{\quad}l} A & B & C \\ a_{1} & b_{1} & c_{1} \\ a_{2} & b_{2} & c_{2} \end{array} \right\vert &=&\left\vert \begin{array}{l@{\quad}l} b_{1} & c_{1} \\[5pt] b_{2} & c_{2} \end{array} \right\vert A-\left\vert \begin{array}{l@{\quad}l} a_{1} & c_{1} \\ a_{2} & c_{2} \end{array} \right\vert B+\left\vert \begin{array}{l@{\quad}l} a_{1} & b_{1} \\ a_{2} & b_{2} \end{array} \right\vert C \\[4pt] &=&( b_{1}c_{2}-b_{2}c_{1}) A-( a_{1}c_{2}-a_{2}c_{1}) B+( a_{1}b_{2}-a_{2}b_{1}) C \end{eqnarray*}
NOTE
Notice the minus sign in the middle term.
EXAMPLE 2Evaluating Determinants
- (a) \left\vert \begin{array}{r@{\quad}r} 2 & 3 \\ -1 & 2 \end{array} \right\vert =(2)(2)-(-1)(3)=4+3=7
- (b) \begin{align*} \left\vert \begin{array}{r@{\quad}r@{\quad}r} A & B & C \\ 2 & 3 & 1 \\ -1 & 2 & -1 \end{array} \right\vert &=\left\vert \begin{array}{r@{\quad}r} 3 & 1 \\ 2 & -1 \end{array} \right\vert A-\left\vert \begin{array}{r@{\quad}r} 2 & 1 \\ -1 & -1 \end{array} \right\vert B+\left\vert \begin{array}{r@{\quad}r} 2 & 3 \\ -1 & 2 \end{array} \right\vert C\\ &=(-3-2)A-(-2+1)B+(4+3)C=-5A+B+7C \end{align*}
NOW WORK
The cross product of the vectors \ \mathbf{v}=v_{1}\mathbf{i}+v_{2}\mathbf{j }+v_{3}\mathbf{k} and \ \mathbf{w}=w_{1}\mathbf{i}+w_{2}\mathbf{j}+w_{3} \mathbf{k}: \begin{equation*} \mathbf{v}\times \mathbf{w}=(v_{2}w_{3}-v_{3}w_{2})\,\mathbf{i} -(v_{1}w_{3}-v_{3}w_{1})\,\mathbf{j}+(v_{1}w_{2}-v_{2}w_{1})\,\mathbf{k} \end{equation*}
can be written symbolically as a determinant. \begin{eqnarray*} \mathbf{v}\times \mathbf{w}& =&\left\vert \begin{array}{l@{\quad}l@{\quad}l} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ v_{1} & v_{2} & v_{3} \\ w_{1} & w_{2} & w_{3} \end{array} \right\vert =\left\vert \begin{array}{l@{\quad}l} v_{2} & v_{3} \\ w_{2} & w_{3} \end{array} \right\vert \,\mathbf{i}-\left\vert \begin{array}{l@{\quad}l} v_{1} & v_{3} \\ w_{1} & w_{3} \end{array} \right\vert \,\mathbf{j}+\left\vert \begin{array}{l@{\quad}l} v_{1} & v_{2} \\ w_{1} & w_{2} \end{array} \right\vert \,\mathbf{k} \\[5pt] & =&(v_{2}w_{3}-v_{3}w_{2})\,\mathbf{i}-(v_{1}w_{3}-v_{3}w_{1})\,\mathbf{j} +(v_{1}w_{2}-v_{2}w_{1})\,\mathbf{k} \end{eqnarray*}
725
EXAMPLE 3Finding a Cross Product Using Determinants
If \mathbf{v}=2\mathbf{i}-\mathbf{j}+\mathbf{k} and \mathbf{w}=4\mathbf{i} +2\mathbf{j}-\mathbf{k}, find
- (a) \mathbf{v}\times \mathbf{w}
- (b) \mathbf{w} \times \mathbf{v}
- (c) \mathbf{v\times v}
Solution (a) \mathbf{v}\times \mathbf{w}=\left\vert \begin{array}{r@{\quad}r@{\quad}r} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ 2 & -1 & 1 \\ 4 & 2 & -1 \end{array} \right\vert =(1-2)\mathbf{i}-(-2-4)\mathbf{j}+(4+4)\mathbf{k}=-\mathbf{i}+6 \mathbf{j}+8\mathbf{k}
(b) \mathbf{w}\times \mathbf{v}=\left\vert \begin{array}{r@{\quad}r@{\quad}r} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ 4 & 2 & -1 \\ 2 & -1 & 1 \end{array} \right\vert =(2-1) \,\mathbf{i}-( 4+2) \,\mathbf{ j\,+\,}( -4-4) \,\mathbf{k=i}-6\mathbf{j}-8\mathbf{k=-}( \mathbf{v}\times \mathbf{w})
(c) \mathbf{v}\times \mathbf{v}=\left\vert \begin{array}{r@{\quad}r@{\quad}r} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ 2 & -1 & 1 \\ 2 & -1 & 1 \end{array} \right\vert =0\,\mathbf{i}-0\,\mathbf{j}+0\mathbf{\,k}=\mathbf{0}
NOTE
The cross product is not a commutative operation. That is, \mathbf{v}\times \mathbf{w}\neq \mathbf{w}\times \mathbf{v}.
NOW WORK
2 Prove Algebraic Properties of the Cross ProductPrinted Page 726
Example 3 illustrates two properties of the cross product. Parts (a) and (b) suggest that \mathbf{v\times w=-}( \mathbf{w\times v}) and (c) suggests that the cross product of a vector with itself equals the zero vector \mathbf{0}. These and other properties of the cross product are listed in the theorem below.
THEOREM Algebraic Properties of the Cross Product
If \mathbf{u}, \mathbf{v}, and \mathbf{w} are vectors in space and if a is a scalar, then
- \mathbf{v}\times \mathbf{v} = \mathbf{0} \tag {1}
- \mathbf{v}\times \mathbf{w} = -(\mathbf{w}\times \mathbf{v}) \tag {2}
- a\, (\mathbf{v}\times \mathbf{w}) = (a\,\mathbf{v}) \times \mathbf{w} = \mathbf{v}\times (a\,\mathbf{w}) \tag {3}
- \mathbf{v}\times (\mathbf{w}+ \mathbf{u}) = (\mathbf{v}\times \mathbf{w}) + (\mathbf{v}\times \mathbf{u}) \tag {4}
- \Vert \mathbf{v}\times \mathbf{w}\Vert^{2} = \Vert \mathbf{v}\Vert^{2}\,\Vert \mathbf{w}\Vert^{2} - (\mathbf{v}\,{\cdot}\, \mathbf{w})^{2} \tag {5}
We prove (1), (2), and (5), and leave the proofs of (3) and (4) as exercises (Problems 56 and 57).
Proof
Let \mathbf{v}=v_{1}\mathbf{i}+v_{2}\mathbf{j}+v_{3} \mathbf{k} and \mathbf{w}=w_{1}\mathbf{i}+w_{2}\mathbf{j}+w_{3}\mathbf{k}.
(1) \mathbf{v}\times \mathbf{v}=(v_{2}v_{3}-v_{2}v_{3})\mathbf{i} -(v_{1}v_{3}-v_{1}v_{3})\mathbf{j}+(v_{1}v_{2}-v_{1}v_{2})\mathbf{k}=\mathbf{ 0}
(2) \begin{array}{@{\hspace*{-6.2pc}}rcl} \mathbf{v}\times \mathbf{w}&=&(v_{2}w_{3}-w_{2}v_{3})\mathbf{i} -(v_{1}w_{3}-w_{1}v_{3})\mathbf{j}+(v_{1}w_{2}-w_{1}v_{2})\mathbf{k}\\[2pt] \mathbf{w}\times \mathbf{v}&=&(w_{2}v_{3}-v_{2}w_{3}) \mathbf{i}-(w_{1}v_{3}-v_{1}w_{3})\,\mathbf{j}+(w_{1}v_{2}-v_{1}w_{2})\, \mathbf{k} \end{array}
Consequently, \mathbf{v}\times \mathbf{w}=-(\mathbf{w}\times \mathbf{v}).
(5) First we find \left\Vert \mathbf{v}\times \mathbf{w}\right\Vert ^{2}. \begin{array}{@{\hspace*{-2.2pc}}rcl} \mathbf{v}\times \mathbf{w} &=&(v_{2}w_{3}-w_{2}v_{3})\mathbf{i}-(v_{1}w_{3}-w_{1}v_{3})\mathbf{j}+(v_{1}w_{2}-w_{1}v_{2})\mathbf{k} \\ \Vert \mathbf{v}\times \mathbf{w}\Vert ^{2} &=&(v_{2}w_{3}-w_{2}v_{3})^{2}+(v_{1}w_{3}-w_{1}v_{3})^{2}+(v_{1}w_{2}-w_{1}v_{2})^{2}\\ &=&[ (v_{2}\,w_{3})^{2}-2v_{2}\,w_{2}\,v_{3}\,w_{3}+(w_{2}\,v_{3})^{2}] +[ (v_{1}w_{3})^{2}-2v_{1}w_{1}v_{3}w_{3}+(w_{1}v_{3})^{2}] \\ &&+\,[ (v_{1}\,w_{2})^{2}-2\,v_{1}\,w_{1}\,v_{2}\,w_{2}+(w_{1}v_{2})^{2}] \end{array}
Then we find \left\Vert \mathbf{v}\right\Vert ^{2}\,\left\Vert \mathbf{w} \right\Vert ^{2}-(\mathbf{v}\,{\cdot}\, \mathbf{w})^{2}. \begin{eqnarray*} \Vert \mathbf{v}\Vert ^{2}\Vert \mathbf{w}\Vert ^{2}-(\mathbf{v}\,{\cdot}\, \mathbf{w})^{2}& =&\big[ \big( v_{1}^{2}+v_{2}^{2}+v_{3}^{2}\big) \big( w_{1}^{2}+w_{2}^{2}+w_{3}^{2}\big) \big] -(v_{1}w_{1}+v_{2}w_{2}+v_{3}w_{3})^{2} \\[4pt] &=& (v_{1}w_{2})^{2}+(v_{1}w_{3})^{2}+(v_{2}w_{1})^{2}+(v_{2}w_{3})^{2}+( v_{3}w_{1}) ^{2}+\left( v_{3}w_{2}\right) ^{2} \\[4pt] && -2v_{1}v_{2}w_{1}w_{2}-2v_{1}v_{3}w_{1}w_{3}-2v_{2}v_{3}w_{2}w_{3} \end{eqnarray*}
Reordering the terms in each equation proves the property.
727
The cross products of the unit vectors \mathbf{i}, \mathbf{j}, and \mathbf{k} are particularly useful: \begin{align*} \mathbf{i}\times \mathbf{j}&=\left\vert \begin{array}{l@{\quad}l@{\quad}l} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ 1 & 0 & 0 \\ 0 & 1 & 0 \end{array} \right\vert =0\mathbf{i}+0\mathbf{j}+\mathbf{k}=\mathbf{k} \\ \mathbf{j}\times \mathbf{k}&=\left\vert \begin{array}{l@{\quad}l@{\quad}l} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array} \right\vert =\mathbf{i}\\ \mathbf{k}\times \mathbf{i} &=\left\vert \begin{array}{l@{\quad}l@{\quad}l} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ 0 & 0 & 1 \\ 1 & 0 & 0 \end{array} \right\vert =\mathbf{j} \end{align*}
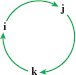
Notice the cyclic pattern for the cross products of \mathbf{i}, \mathbf{j}, and \mathbf{k}: \bbox[5px, border:1px solid black, #F9F7ED]{ \mathbf{i}\times \mathbf{j}=\mathbf{k}\qquad \mathbf{j}\times \mathbf{k}=\mathbf{i} \qquad \mathbf{k}\times \mathbf{i}=\mathbf{j} }
Figure 45 may be helpful in remembering this pattern.
The remaining cross products involving the unit vectors \mathbf{i}, \mathbf{j}, and \mathbf{k} are listed below. They are consequences of algebraic properties (1) and (2) of the cross product. \bbox[5px, border:1px solid black, #F9F7ED]{ \begin{array}{rcl@{\qquad}rcl@{\qquad}rcl} \mathbf{j}\times \mathbf{i}&=&-\mathbf{k} & \mathbf{k}\times \mathbf{j}&=&-\mathbf{i} & \mathbf{i}\times \mathbf{k}&=&-\mathbf{j} \\[3pt] \mathbf{i}\times \mathbf{i} &=& {\bf 0} & \mathbf{j}\times \mathbf{j} &=& {\bf 0} & \mathbf{k}\times \mathbf{k} &=& {\bf 0} \end{array} }
3 Apply Geometric Properties of the Cross ProductPrinted Page 727
Besides useful algebraic properties, the cross product has important geometric properties.
THEOREM Geometric Properties of the Cross Product
If \mathbf{v} and \mathbf{w} are two nonzero vectors in space, then
- \mathbf{v}\times \mathbf{w} is orthogonal to both \mathbf{v} and \mathbf{w} \tag {6}
- \Vert \mathbf{v}\times \mathbf{w}\Vert \,=\Vert \mathbf{v}\Vert \Vert \mathbf{w}\Vert \sin \theta , where \theta is the angle between \mathbf{v} and \mathbf{w} \tag {7}
- \Vert \mathbf{v}\times \mathbf{w}\Vert is the area of the parallelogram having \mathbf{v} and \mathbf{w} as adjacent sides \tag {8}
- \mathbf{v}\times \mathbf{w}=\mathbf{0} if and only if \mathbf{v} and \mathbf{w} are parallel vectors \tag {9}
Proof of (6)
Let \mathbf{v}=v_{1}\mathbf{i}+v_{2}\mathbf{j}+v_{3} \mathbf{k} and \mathbf{w}=w_{1}\mathbf{i}+w_{2}\mathbf{j}+w_{3}\mathbf{k}. Then \mathbf{v}\times \mathbf{w}=(v_{2}w_{3}-w_{2}v_{3})\mathbf{i} -(v_{1}w_{3}-w_{1}v_{3})\mathbf{j}+(v_{1}w_{2}-w_{1}v_{2})\mathbf{k}
We show that \mathbf{v}\times \mathbf{w} is orthogonal to \mathbf{v} by computing the dot product \mathbf{v}\,{\cdot}\, (\mathbf{v}\times \mathbf{w}). \begin{eqnarray*} \mathbf{v}\,{\cdot}\, (\mathbf{v}\times \mathbf{w}) &=&v_{1}( v_{2}w_{3}-w_{2}v_{3}) -v_{2}( v_{1}w_{3}-w_{1}v_{3}) +v_{3}( v_{1}w_{2}-w_{1}v_{2}) \\[3pt] &=&v_{1}v_{2}w_{3}-v_{1}w_{2}v_{3}-v_{2}v_{1}w_{3}+v_{2}w_{1}v_{3}+v_{3}v_{1}w_{2}-v_{3}w_{1}v_{2}=0 \end{eqnarray*}
So, \mathbf{v}\times \mathbf{w} is orthogonal to \mathbf{v}.
Now we show \mathbf{v}\times \mathbf{w} is orthogonal to \mathbf{w} by computing the dot product \mathbf{w}\,{\cdot}\, (\mathbf{v}\times \mathbf{w}). \begin{eqnarray*} \mathbf{w}\,{\cdot}\, (\mathbf{v}\times \mathbf{w}) &=&w_{1} ( v_{2}w_{3}-w_{2}v_{3}) -w_{2} ( v_{1}w_{3}-w_{1}v_{3}) +w_{3} ( v_{1}w_{2}-w_{1}v_{2}) \\[3pt] &=&w_{1}v_{2}w_{3}-w_{1}w_{2}v_{3}-w_{2}v_{1}w_{3}+w_{2}w_{1}v_{3}+w_{3}v_{1}w_{2}-w_{3}w_{1}v_{2}=0 \end{eqnarray*}
So, \mathbf{v}\times \mathbf{w} is orthogonal to \mathbf{w}.
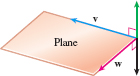
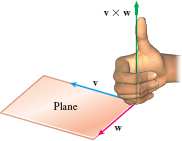
Any two nonparallel vectors \mathbf{v} and \mathbf{w} lie in a single plane. Since the vector \mathbf{v}\times \mathbf{w} is orthogonal to both vectors \mathbf{v} and \mathbf{w}, it follows that the vector \mathbf{ v\times w} is normal to the plane containing \mathbf{v} and \mathbf{w}. As Figure 46 illustrates, there actually are two directions that are normal to the plane containing \mathbf{v} and \mathbf{w}; one directed up and the other directed down. Which is the direction of \mathbf{v\times w}? It can be shown that the direction of \mathbf{v}\times \mathbf{w} is determined by the thumb of the right hand when the other fingers of the right hand are cupped so that they point in the direction from \mathbf{v} to \mathbf{w}, as shown in Figure 47. As in Section 10.1, this is usually referred to as the right-hand rule.
728
EXAMPLE 4Finding a Vector Orthogonal to Two Given Vectors
Find a vector orthogonal to the vectors \mathbf{v}=2\mathbf{i}-\mathbf{j}+ \mathbf{k} and \mathbf{w}=2\mathbf{i}+2\mathbf{j}-\mathbf{k}.
Solution Since \mathbf{v\times w} is orthogonal to both the vector \mathbf{v} and the vector \mathbf{w}, a vector orthogonal to \mathbf{v} and \mathbf{w} is \mathbf{v}\times \mathbf{w}= \left|\begin{array}{c@{\quad}c@{\quad}c} \mathbf{i} & \hphantom{-}\mathbf{j} & \hphantom{-}\mathbf{k} \\[3pt] 2 & -1 & \hphantom{-}1 \\[3pt] 2 & \hphantom{-}2 & -1 \end{array}\right| =-\mathbf{i}+4\mathbf{j}+6\mathbf{k}
NOW WORK
Next we prove Property (7).
Property (7): \Vert \mathbf{v}\times \mathbf{w}\Vert \,=\Vert \mathbf{v} \Vert \Vert \mathbf{w}\Vert \sin \theta , where \theta is the angle between \mathbf{v} and \mathbf{w}.
Proof of (7)
Let \theta be the angle between the nonzero vectors \mathbf{v} and \mathbf{w}. Then from algebraic property (5), we have \begin{equation*} \Vert \mathbf{v}\times \mathbf{w}\Vert ^{2}=\Vert \mathbf{v}\Vert ^{2}\Vert \mathbf{w}\Vert ^{2}-(\mathbf{v}\,{\cdot}\, \mathbf{w})^{2}\tag {5} \end{equation*}
Since \cos \theta =\dfrac{\mathbf{v}\,{\cdot}\, \mathbf{w}}{\left\Vert \mathbf{v} \right\Vert \left\Vert \mathbf{w}\right\Vert }, we have \mathbf{v}\,{\cdot}\, \mathbf{w=}\left\Vert \mathbf{v}\right\Vert \left\Vert \mathbf{w}\right\Vert \cos \theta and \begin{align*} \Vert \mathbf{v}\times \mathbf{w}\Vert ^{2}&=\Vert \mathbf{v}\Vert^{2}\Vert \mathbf{w}\Vert ^{2}-\Vert \mathbf{v}\Vert ^{2}\Vert \mathbf{w} \Vert ^{2}\cos ^{2}\theta & {\color{#0066A7}{\hbox{\({(\mathbf{v}\,{\cdot}\, \mathbf{w})}^{2}{=\Vert \mathbf{v}\Vert }^{2}{\Vert \mathbf{w}\Vert }^{2}\cos ^{2}{\theta }\)}}} \\ &=\Vert \mathbf{v}\Vert ^{2}\Vert \mathbf{w}\Vert ^{2}(1-\cos ^{2}\theta )&{\color{#0066A7}{\hbox{Factor out \(\Vert \mathbf{v}\Vert ^{2} \Vert \mathbf{w}\Vert ^{2}\)}}}\\ &=\Vert \mathbf{v}\Vert ^{2}\Vert \mathbf{w}\Vert ^{2}\sin ^{2}\theta & {\color{#0066A7}{\hbox{\(1-\cos ^{2}\theta =\sin ^{2}\theta\)}}} \end{align*}
Since 0\leq \theta \leq \pi , we know \sin \theta \geq 0. Now take the square root of both sides to obtain \Vert \mathbf{v}\times \mathbf{w} \Vert =\Vert \mathbf{v}\Vert \Vert \mathbf{w}\Vert \sin \theta .
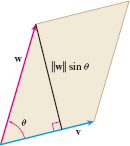
Property (7) is used to prove property (8): \left\Vert \mathbf{v}\times \mathbf{w}\right\Vert equals the area of the parallelogram with adjacent sides \mathbf{v} and \mathbf{w}.
Proof of (8)
If \mathbf{v} and \mathbf{w} are nonzero vectors and \theta is the angle between \mathbf{v} and \mathbf{w}, then \Vert \mathbf{v}\Vert and \Vert \mathbf{w}\Vert represent the lengths of the sides of a parallelogram. As shown in Figure 48, the base of the parallelogram is \left\Vert \mathbf{v}\right\Vert and its altitude is \left\Vert \mathbf{w}\right\Vert \sin \theta , so its area A is \begin{equation*} A=\hbox{ (base)(altitude)}=\left\Vert \mathbf{v}\right\Vert \left\Vert \mathbf{w}\right\Vert \sin \theta \end{equation*}
Since \Vert \mathbf{v}\times \mathbf{w}\Vert =\Vert \mathbf{v}\Vert \Vert \mathbf{w}\Vert \sin \theta , the magnitude of \mathbf{v}\times \mathbf{w} is the area of the parallelogram whose sides are the vectors \mathbf{v} and \mathbf{w}.
EXAMPLE 5Finding the Area of a Parallelogram
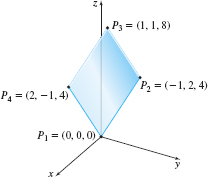
Find the area A of the parallelogram shown in Figure 49, which has vertices at the points P_{1}=(0, 0, 0), P_{2}=(-1, 2, 4), P_{3}=(1, 1, 8), and P_{4}=(2, -1, 4).
Solution The area A of a parallelogram is \Vert \mathbf{v} \times \mathbf{w}\Vert , where \mathbf{v} and \mathbf{w} are two adjacent sides of the parallelogram. Be careful! Not all pairs of vertices give a side. For example, \overrightarrow{P_{1}~P_{3}} is not a side; it is a diagonal of the parallelogram. It is helpful to sketch the parallelogram before choosing \mathbf{v} and \mathbf{w}. Choose \begin{equation*} \mathbf{v}=\overrightarrow{P_{1}~P_{2}}= \left\langle -1,\,2,4\right\rangle =-\mathbf{i}+2\mathbf{j}+4\mathbf{k} \end{equation*}
729
and \begin{equation*} \hbox{}\mathbf{w}=\overrightarrow{P_{1}~P_{4}} =\left\langle 2,-1,4\right\rangle =2\mathbf{i}-\mathbf{j}+4\mathbf{k} \end{equation*}
Then \begin{equation*} \mathbf{v}\times \mathbf{w}= \left|\begin{array}{r@{\quad}r@{\quad}r} \mathbf{i} & \mathbf{j} & \mathbf{k} \\[3pt] -1 & 2 & 4 \\[3pt] 2 & -1 & 4 \end{array}\right| =12\mathbf{i}+12\mathbf{j}-3\mathbf{k} \end{equation*}
The area of the parallelogram is \left\Vert \mathbf{v}\times \mathbf{w}\right\Vert = \sqrt{144+144+9}= \sqrt{297} \approx 17.234~\hbox{square units}
NOW WORK
Property (9): \mathbf{v}\times \mathbf{w}=\mathbf{0} if and only if \mathbf{v} and \mathbf{w} are parallel nonzero vectors.
Proof of (9)
If \mathbf{v} and \mathbf{w} are parallel nonzero vectors, then the angle \theta between the vectors \mathbf{v} and \mathbf{w} is either \theta =0 or \theta =\pi . For either angle, \sin \theta =0, and \begin{equation*} \left\Vert \mathbf{v}\times \mathbf{w}\right\Vert =\Vert \mathbf{v}\Vert \Vert \mathbf{w}\Vert \sin \theta =0\qquad \hbox{so}\quad \mathbf{v}\times \mathbf{w }=\mathbf{0} \end{equation*}
Now suppose \mathbf{v}\times \mathbf{w}=\mathbf{0}. Since \left\Vert \mathbf{v}\times \mathbf{w}\right\Vert =\Vert \mathbf{v}\Vert \Vert \mathbf{w }\Vert \sin \theta , we have \begin{eqnarray*} \Vert \mathbf{v}\Vert \left\Vert \mathbf{w}\right\Vert \sin \theta &=&0 \\ \sin \theta &=&0 & {\color{#0066A7}{\hbox{\(\mathbf{v} \neq \mathbf{0},\quad \mathbf{w}\neq \mathbf{0}\)}}} \\ \theta &=&0\quad\hbox{or}\quad \theta =\pi \end{eqnarray*}
That is, the vectors \mathbf{v} and \mathbf{w} are parallel.
EXAMPLE 6Verifying Two Vectors Are Parallel
Show that the vectors \mathbf{v}=2\mathbf{i}+\mathbf{j}-\mathbf{k} and \mathbf{w}=-4\mathbf{i}-2\mathbf{j}+2\mathbf{k} are parallel.
Solution We show that \mathbf{v}\times \mathbf{w}=\mathbf{0}. \begin{eqnarray*} \mathbf{v}\times \mathbf{w}&=&\left\vert \begin{array}{r@{\quad}r@{\quad}r} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ 2 & 1 & -1 \\ -4 & -2 & 2 \end{array} \right\vert =\left\vert \begin{array}{r@{\quad}r} 1 & -1 \\ -2 & 2 \end{array} \right\vert \,\mathbf{i}-\left\vert \begin{array}{r@{\quad}r} 2 & -1 \\ -4 & 2 \end{array} \right\vert \,\mathbf{j}+\left\vert \begin{array}{r@{\quad}r} 2 & 1 \\ -4 & -2 \end{array} \right\vert \,\mathbf{k}\\[5pt] &=&0\mathbf{i}+0\mathbf{j}+0\mathbf{k}=\mathbf{0} \end{eqnarray*}
For the vectors \mathbf{v} and \mathbf{w} in Example 6, notice that \mathbf{w}=-2\mathbf{v}. So, the magnitude of \mathbf{w} is twice that of \mathbf{v}, and \mathbf{v} and \mathbf{w} are opposite in direction.
Application: Angular VelocityPrinted Page 729
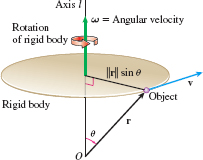
Figure 50 illustrates a rigid body that is rotating about a fixed axis l with a constant angular speed \omega. The angular velocity {\omega } is defined as the vector of magnitude \omega whose direction is parallel to the axis l, so that if the fingers of the right hand are wrapped about l in the direction of the rotation, the thumb will point in the direction of {\omega }.
We seek a formula for the velocity \mathbf{v} of an object on the rigid body. Let the origin O be on the axis l of rotation, let \mathbf{r} denote the position of the object, and let \theta be the angle between \mathbf{r} and the axis l. The motion of the object is circular. Since \left\Vert \mathbf{r}\right\Vert \sin \theta equals the distance of the object from the axis l, \left\Vert { r}\right\Vert \sin \theta is the radius of the circle. As a result, we have \left\Vert \mathbf{v}\right\Vert =\left\Vert {\omega }\right\Vert \Vert \mathbf{r}\Vert \sin \theta\qquad {\color{#0066A7}{v=r\omega}}\qquad {\color{#0066A7}{\hbox{(linear speed \(=\) angular speed \(\times\) radius)}}}
NEED TO REVIEW?
Circular motion is discussed in Appendix A.4, p. A-27.
730
Since the velocity is tangent to the circle of motion, the velocity \mathbf{ v} is normal to the plane formed by \mathbf{r} and {\omega .} That is, \mathbf{v} is parallel to {\omega }\times \mathbf{r}. Using the right-hand rule to define {\omega }, the velocity \mathbf{v} is in the direction of {\omega }\times \mathbf{r}. Since the magnitude of {\omega }\times \mathbf{r} is \begin{equation*} \left\Vert {\omega }\times \mathbf{r}\right\Vert =\Vert { \omega }\Vert \Vert \mathbf{r}\Vert \sin \theta =\Vert \mathbf{v}\Vert \end{equation*}
it follows that \bbox[5px, border:1px solid black, #F9F7ED]{ \mathbf{v}={\omega }\times \mathbf{r} }
EXAMPLE 7Finding the Speed of an Object in Circular Motion
A rigid body rotates with a constant angular speed of \omega radians per second about a line through the origin in the direction of the vector 2 \mathbf{i}+\mathbf{j}+2\mathbf{k}. Find the speed of an object on this body at the instant the object passes through the point (1,3,5). Assume the distance is in meters.
Solution The vector {\omega } is parallel to the axis of rotation of the rigid body, and so it is in the direction of the vector 2 \mathbf{i}+\mathbf{j}+2\mathbf{k}. Since \dfrac{2\mathbf{i}+\mathbf{j}+2 \mathbf{k}}{ \sqrt{2^{2}+1^{2}+2^{2}}}=\dfrac{2}{3}\mathbf{i}+\dfrac{1}{3} \mathbf{j}+\dfrac{2}{3}\mathbf{k} is a unit vector in the direction of 2 \mathbf{i}+\mathbf{j}+2\mathbf{k}, the angular velocity {\omega } is \begin{equation*} {\omega }=\omega \left( \frac{2}{3}\,\mathbf{i}+\frac{1}{3}\,\mathbf{j }+\frac{2}{3}\,\mathbf{k}\right) \end{equation*}
The position of the object is \mathbf{r}=\mathbf{i}+3\mathbf{j}+5\mathbf{k}. So, the velocity \mathbf{v} of the object is \begin{eqnarray*} \mathbf{v}&=& {\omega }\times \mathbf{r}=\left[ \omega \left( \frac{2}{ 3}\,\mathbf{i}+\frac{1}{3}\,\mathbf{j}+\frac{2}{3}\,\mathbf{k}\right) \right] \times \left[ \mathbf{i}+3\mathbf{j}+5\mathbf{k}\right] =\,\omega \left\vert \begin{array}{l@{\quad}l@{\quad}l} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ \dfrac{2}{3} & \dfrac{1}{3} & \dfrac{2}{3} \\ 1 & 3 & 5 \end{array} \right\vert\\[5pt] &=&\omega \left( -\dfrac{1}{3}\mathbf{i}-\dfrac{8}{3}\mathbf{j}+ \dfrac{5}{3}\mathbf{k}\right) \end{eqnarray*}
The speed v of the object is v=\left\Vert \mathbf{v}\right\Vert =\omega \sqrt{\dfrac{1}{9}+\dfrac{64}{9}+\dfrac{25}{9}}= \sqrt{10}\,\omega meters per second.