14.4 Center of Mass; Moment of InertiaPrinted Page 929
OBJECTIVES
When you finish this section, you should be able to:
1 Find the Mass and the Center of Mass of a LaminaPrinted Page 929
NEED TO REVIEW?
The center of mass of a homogeneous lamina is discussed in Section 6.8, pp. 460-464.
In many applications, thin sheets of material, such as copper stripping, are treated as if they were two-dimensional. A lamina is a plane area that represents a thin, flat sheet of material. If the mass density of the material is constant, the lamina is called homogeneous. The mass M of a homogeneous lamina is ρA, where A is the area of the lamina and ρ is its constant mass density.
RECALL
The mass density of a two-dimensional material is defined as the mass per unit area of the material. In SI units, mass density is measured in kilograms per meter squared; in U.S. customary units, it is measured in slugs per foot squared.
However, materials usually are not homogeneous and so the mass density is variable. Suppose a lamina is represented by a closed, bounded region R of the xy-plane and its mass density ρ=ρ(x,y) varies continuously over R. To find the mass M of this lamina, we use double integration.
We begin by partitioning the region R into n rectangles, as in Figure 32 on page 930. Then, in each rectangle Ri of area ΔAi, we choose a point (ui,vi). An approximation to the mass Mi of the ith rectangle is \bbox[5px, border:1px solid black, #F9F7ED]{ M_i=[\hbox{Mass density}] \times [\hbox{Area}] =\rho (u_{i},v_{i})\Delta A_{i} }
930
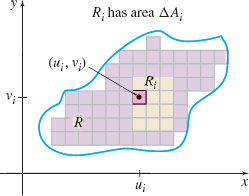
By adding up the masses of all the rectangles, the mass M of the lamina can be approximated by M\approx \sum\limits_{i=1}^{n}\rho (u_{i},v_{i})\Delta A_{i}
If the norm \left\Vert P\right\Vert , defined to be the length of the diagonal of the largest rectangle of the partition, is allowed to approach 0 , then the mass M of the lamina is given by a double integral: \bbox[5px, border:1px solid black, #F9F7ED]{ M=\lim\limits_{\Vert P\Vert \rightarrow 0}\sum\limits_{i=1}^{n}\rho (u_{i},v_{i})\Delta A_{i}=\displaystyle\iint\limits_{\kern-3ptR}\rho (x,y)\,{\it dA} }
NOTE
Observe that if the mass density \rho is constant, then the formula for the mass of the lamina reduces to M=\iint\limits_{\kern-3ptR}\rho \,{\it dA}=\rho \iint\limits_{\kern-3ptR} \,{\it dA}=\rho A where A is the area of the region R.
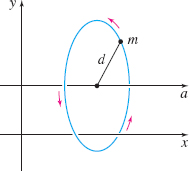
If a particle of mass m is located a distance d from a fixed axis a, the moment of mass M_{a} of the particle about the a-axis is defined as \bbox[5px, border:1px solid black, #F9F7ED]{ M_{a}=md }
The moment of mass M_{a} measures the tendency of the particle to rotate about the a-axis.
NEED TO REVIEW?
Moments of mass were discussed in Section 6.8, p. 459.
Look again at Figure 32. Suppose the region R represents a lamina of variable mass density \rho =\rho (x,y) . We partition R into n rectangles and consider the ith rectangle R_{i} whose area is \Delta A_{i}. We choose a point (u_{i},v_{i}) in R_{i}. Then the moment of mass M_{i} about the x-axis of the ith rectangle is approximated by \bbox[5px, border:1px solid black, #F9F7ED]{ M_{i}= [\hbox{Mass}] \times [\hbox{Distance from the } x\hbox{-axis}] =[\rho (u_{i},v_{i})\Delta A_{i}](v_{i}) }
NOTE
Sometimes M_{a} is referred to as the first moment of the particle about the axis a.
By summing all the moments m_{i} about the x-axis and taking the limit as the norm \left\Vert P\right\Vert approaches 0, we obtain the moment of mass M_{x} about the x-axis of the lamina. \bbox[5px, border:1px solid black, #F9F7ED]{ M_{x}=\lim\limits_{\Vert P\Vert \rightarrow 0}\sum\limits_{i=1}^{n}v_{i}\,\rho (u_{i},v_{i})\,\Delta A_{i}=\displaystyle\iint\limits_{\kern-3ptR}y\,\rho (x,y)\,{\it dA} }
Similarly, the moment of mass M_{y} about the y-axis of the lamina is given by \bbox[5px, border:1px solid black, #F9F7ED]{ M_{y}=\lim\limits_{\Vert P\Vert \rightarrow 0}\sum\limits_{i=1}^{n}u_{i}\,\rho (u_{i},v_{i})\,\Delta A_{i}=\displaystyle\iint\limits_{\kern-3ptR}x\,\rho (x,y)\,{\it dA} }
THEOREM Mass of the Lamina
Suppose a lamina of variable mass density \rho =\rho (x,y) is represented by a closed, bounded region R of the xy-plane. If \rho is continuous on R, then the mass of the lamina is \bbox[5px, border:1px solid black, #F9F7ED]{ M=\displaystyle\iint\limits_{\kern-3ptR}\rho (x,y)\,{\it dA} }
The moment of mass about the the x-axis is \bbox[5px, border:1px solid black, #F9F7ED]{ M_{x}=\displaystyle\iint\limits_{\kern-3ptR}y\rho (x,y)\,{\it dA} }
The moment of mass about the y-axis is \bbox[5px, border:1px solid black, #F9F7ED]{ M_{y}=\displaystyle\iint\limits_{\kern-3ptR}x \rho (x,y)\,{\it dA} }
931
The center of mass of a lamina is the point (\bar{x},\bar{ y}) whose coordinates satisfy the equations \bbox[5px, border:1px solid black, #F9F7ED]{ \bar{x}=\dfrac{M_{y}}{M}=\dfrac{\displaystyle\iint\limits_{\kern-3ptR}x\rho (x,y)\,{\it dA}}{\displaystyle\iint\limits_{\kern-3ptR}\rho (x,y)\,{\it dA}}\qquad \qquad \bar{y}= \dfrac{M_{x}}{M}=\dfrac{\displaystyle\iint\limits_{\kern-3ptR}y\rho (x,y)\,{\it dA}}{ \displaystyle\iint\limits_{\kern-3ptR}\rho (x,y)\,{\it dA}} }
We distinguish between the center of mass (or center of gravity) of a lamina, which is defined by (\bar{x},\bar{y})= \left( \dfrac{M_{y}}{M},\dfrac{M_{x}}{M}\right) , and the centroid of a lamina. The centroid is a purely geometric property of the lamina; it coincides with the center of mass in the case of a homogeneous lamina. To see the distinction, a square lamina always has its centroid at the (geometric) center, but the same square with variable density will almost always have its center of mass off-center.
For a physical interpretation, suppose a piece of string is attached to the lamina at the center of mass (\bar{x},\bar{y}). Then the lamina, when suspended from the string, will hang in a horizontal position.
EXAMPLE 1Finding the Mass and the Center of Mass of a Lamina
Find the mass and center of mass of a lamina in the shape of an isosceles right triangle. The mass density function \rho =\rho (x,y) is directly proportional to the square of the distance from the vertex at the right angle.
Solution We position the lamina in the xy-plane so that the vertex at the right angle is at the origin and the two equal sides lie along the positive coordinate axes. See Figure 33. Suppose the equal sides of the triangle each measure a.
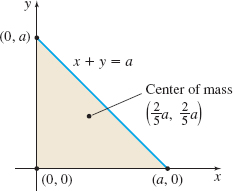
Since the distance of a point (x,y) from the origin is \sqrt{ x^{2}+y^{2}}, the mass density of the lamina is \rho (x,y)=k(x^{2}+y^{2})
where k is the constant of proportionality. Since \rho =\rho (x,y) is continuous on R, the mass M of this lamina is given by a double integral. \begin{eqnarray*} M& =&\displaystyle\iint\limits_{\kern-3ptR}\rho (x,y)\,{\it dA}=\displaystyle\iint\limits_{\kern-3ptR}k(x^{2}+y^{2})\,d\!A=k\int_{0}^{a} \int_{0}^{a-x}(x^{2}+y^{2})\,{\it dy}\,{\it dx}\\[4pt] &=&k\int_{0}^{a}\left[ \left( x^{2}y+\dfrac{ y^{3}}{3}\right) \right] _{0}^{a-x}{\it dx} = k\int^a_0 \left[x^2a -x^3+\dfrac{(a-x)^3}{3}\right] {\it dx}\\[4pt] & =& k\int_{0}^{a}\dfrac{1}{3}(a^{3}-3a^{2}x+6ax^{2}-4x^{3})\,{\it dx} =\dfrac{k}{3} \left[a^3x-3a^2 \dfrac{x^2}{2} +2ax^3 -x^4\right]^a_0\\[4pt] &=&\dfrac{k}{3}\left( a^{4}-\dfrac{3a^{4}}{2}+2a^{4}-a^{4}\right) =\dfrac{ka^{4}}{6} \end{eqnarray*}
Due to the symmetry of both the region R and the mass density, the center of mass (\bar{x},\bar{y}) lies on the line y=x. So, once we find \bar{ x}, we also know \bar{y}. The moment of mass with respect to the y-axis, M_{y}, is \begin{eqnarray*} M_{y}& =& \displaystyle\iint\limits_{\kern-3ptR}x\rho (x,y)\,{\it dA}=\displaystyle\iint\limits_{\kern-3ptR}xk(x^{2}+y^{2})\,d\!A=k\int_{0}^{a} \int_{0}^{a-x}(x^{3}+xy^{2})\,{\it dy}\,{\it dx} \\[4pt] & =&\dfrac{k}{3}\int_{0}^{a}(a^{3}x-3a^{2}x^{2}+6ax^{3}-4x^{4})\,{\it dx}=\dfrac{ka^{5}}{15} \end{eqnarray*}
932
The center of mass (\bar{x},\bar{y}) is: \bar{x}=\dfrac{M_{y}}{M}=\dfrac{\dfrac{ka^{5}}{15}}{\dfrac{ka^{4}}{6}}=\dfrac{2}{5}a=\overline{y}
The center of mass of the lamina is the point \left( \dfrac{2}{5}a,\dfrac{2}{5}a\right) .
NOW WORK
EXAMPLE 2Finding the Mass and the Center of Mass of a Lamina
Find the mass M and the center of mass (\bar{x},\bar{y}) of a lamina in the shape of a region R in the xy-plane that lies outside the circle x^{2}+y^{2}=a^{2} and inside the circle x^{2}+y^{2}=2ax. The mass density \rho is inversely proportional to the distance from the origin.
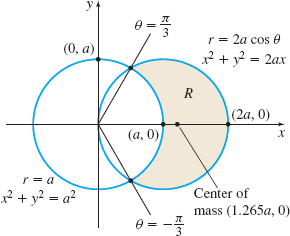
Solution Figure 34 illustrates the region R. Since R involves two circles, we use polar coordinates. Then the two circles are given by r=a and by r=2a\cos \theta . The circles intersect when a=2a\cos \theta or \cos \theta =\dfrac{1}{2}, and the points of intersection are \left( a,\dfrac{\pi }{3}\right) and \left( a,-\dfrac{\pi }{3}\right) . The region R is given by a\leq r\leq 2a\cos \theta , -\dfrac{\pi }{3}\leq \theta \leq \dfrac{\pi }{3}.
Since the distance of a point (x,y) from the origin is \sqrt{x^{2}+y^{2}} , the mass density of the lamina at any point (x,y) in R is \rho (x,y)=\dfrac{k}{\sqrt{x^{2}+y^{2}}}=\dfrac{k}{r} \qquad {\color{#0066A7}{\hbox{\(r^{2} =x^{2} + y^{2}\)}}}
where k is the constant of proportionality. Since R does not contain the origin, the mass density \rho =\rho (x,y) is continuous on R. The mass M of the lamina is \begin{eqnarray*} M &=&\displaystyle\iint\limits_{\kern-3ptR}\rho (x,y)\,{\it dA}=k\displaystyle\iint\limits_{\kern-3ptR}\dfrac{rdr\,d\theta }{r} =k\int_{-\pi /3}^{\pi /3}\int_{a}^{2a\cos \theta }\,dr\,d\theta \\[4pt] &=&k \int_{-\pi /3}^{\pi /3}(2a\cos \theta -a)\,d\theta =k\big[2a\sin \theta -a\theta \big] _{-\pi /3}^{\pi /3}= k\!\left( 2a\sqrt{3}-a\dfrac{2\pi }{3}\right)\\[4pt] &=&\dfrac{2ka}{3}(3\sqrt{3}-\pi ) \end{eqnarray*}
Both the mass density function and the region R are symmetric about the x-axis. So, the center of mass lies on the x-axis; that is, \bar{y}=0. To find \bar{x}, we first find M_{y}. \begin{eqnarray*} M_{y}& =&\displaystyle\iint\limits_{\kern-3ptR}x\rho (x,y)\,{\it dA}=\displaystyle\iint\limits_{\kern-3ptR}( r\cos \theta ) \left( \dfrac{k}{r}\right) r\,dr\,d\theta =k\int_{-\pi /3}^{\pi /3}\int_{a}^{2a\cos \theta }r\cos \theta \,dr\,d\theta\\[4pt] &=&\dfrac{k}{2}\int_{-\pi /3}^{\pi /3}(4a^{2}\cos ^{2}\theta -a^{2})\cos \theta \,d\theta = a^{2}\dfrac{k}{2}\int_{-\pi /3}^{\pi /3}(3-4\sin ^{2}\theta )\cos \theta \,d\theta\\[4pt] &=&\dfrac{a^{2}k}{2}\left[ 3\sin \theta -\dfrac{4\sin ^{3}\theta }{3} \right] _{-\pi /3}^{\pi /3}=ka^{2}\sqrt{3} \end{eqnarray*}
Then \bar{x}=\dfrac{M_{y}}{M}=\dfrac{ka^{2}\sqrt{3}}{\dfrac{2ka}{3}(3\sqrt{3}-\pi )} =\dfrac{3a\sqrt{3}}{2(3\sqrt{3}-\pi )}\approx 1.265a
The center of mass is approximately (1.265a,0).
NOW WORK
2 Find Moments of InertiaPrinted Page 933
933
In rectilinear motion, the mass m of an object can be thought of as a measure of the natural resistance of the object to being accelerated. In rotational motion, the inertia I of an object can be thought of as a measure of the resistance of the object to being rotated about an axis.
Suppose an object of mass m is located a distance d from a fixed axis a. Then its tendency to rotate about the a-axis, called the moment of inertia I_{a}, is defined as \bbox[5px, border:1px solid black, #F9F7ED]{ I_{a}=md^{2} }
See Figure 35.
Proceeding as we did for moments of mass, the moment of inertia I_{x} about the x-axis of a lamina of variable mass density \rho (x, y) represented by a closed, bounded region R of the xy-plane is given by \bbox[5px, border:1px solid black, #F9F7ED]{ I_{x}=\lim\limits_{\Vert P\Vert \rightarrow 0}\sum\limits_{i=1}^{n}\underset{\color{#0066A7}{\hbox{Mass}}}{\underbrace{\rho (u_{i},v_{i})\Delta A_{i}}}\underset{\underset{\color{#0066A7}{\hbox{\(x\)-axis squared}}}{\color{#0066A7}{\hbox{Distance from}}}}{\underbrace{v_{i}^{2}}}=\displaystyle\iint\limits_{\kern-3ptR}y^{2}\rho (x, y)\,{\it dA} }
NOTE
The moment of inertia I_{a} is often referred to as the second moment of the particle about the axis a. It is called the second moment because the distance is squared.
Similarly, the moment of inertia I_{y} about the y-axis is given by \bbox[5px, border:1px solid black, #F9F7ED]{ I_{y}=\lim\limits_{\Vert P\Vert \rightarrow 0}\sum\limits_{i=1}^{n}\underset{\color{#0066A7}{\hbox{Mass}}}{\underbrace{\rho (u_{i},v_{i})\Delta A_{i}}}\underset{\underset{\color{#0066A7}{\hbox{\(y\)-axis squared}}}{\color{#0066A7}{\hbox{Distance from}}}}{\underbrace{u_{i}^{2}}}=\displaystyle\iint\limits_{\kern-3ptR}x^{2}\rho (x,y)\,{\it dA} }
and the moment of inertia I_{O} about the origin (the z-axis) is given by \bbox[5px, border:1px solid black, #F9F7ED]{ I_{O}=\lim\limits_{\Vert P\Vert \rightarrow 0}\sum\limits_{i=1}^{n}\underset{\color{#0066A7}{\hbox{Mass}}}{\underbrace{\rho (u_{i},v_{i})\Delta A_{i}}}\underset{\underset{\color{#0066A7}{\hbox{origin squared}}}{\color{#0066A7}{\hbox{Distance from the}}}}{\underbrace{\big( u_{i}^{2}+v_{i}^{2}\big) }\,\,} =\displaystyle\iint\limits_{\kern-3ptR}(x^{2}+y^{2}) \rho (x,y)\,{\it dA} }
The moment of inertia I_{O} about the origin is sometimes referred to as the polar moment of inertia or the polar second moment.
Using the sum property of double integrals, the sum of the moments of inertia about the x-axis and the y-axis equals the moment of inertia about the origin. That is, \bbox[5px, border:1px solid black, #F9F7ED]{ I_{x}+I_{y}=I_{O} }
The polar moment of inertia is often used to find the moments I_{x} and I_{y} when there is symmetry, that is, when I_{x}=I_{y}.
EXAMPLE 3Finding Moments of Inertia
- (a) Find the polar moment of inertia I_{O} of a homogeneous lamina of mass density \rho in the shape of a region R in the xy-plane enclosed by the circle x^{2}+y^{2}=a^{2}, a \gt 0.
- (b) Use the polar moment to find the moments of inertia I_{x} and I_{y} of the lamina.
Solution (a) The region R is circular so we use polar coordinates (r, \theta). Then 0\leq r\leq a, 0\leq \theta \leq 2\pi , and {\it dA}=r\,dr\, d\theta . The polar moment of inertia is \begin{eqnarray*} I_{O}&=& \displaystyle\iint\limits_{\kern-3ptR}(x^{2}+y^{2}) \rho (x,y) \,{\it dA} \underset{\underset{\color{#0066A7}{\hbox{\(x^{2}+y^{2}=r^{2}\)}}}{\color{#0066A7}{\uparrow }}}{=}\iint\limits_{\kern-3ptR}r^{2}\rho \,r\,{\it dr}\,d\theta \underset{\underset{\color{#0066A7}{\hbox{\(\rho\) is constant}}}{\color{#0066A7}{\uparrow }}}{=}\rho \int_{0}^{2\pi }\!\!\!\int_{0}^{a}r^{3}\,dr\,d\theta\\ &=&\rho \int_{0}^{2\pi }\dfrac{a^{4}}{4} \,d\theta =\dfrac{\pi a^{4}\rho }{2} \end{eqnarray*}
934
(b) By symmetry, the moment of inertia about the x-axis, I_{x}, equals the moment of inertia about the y-axis, I_{y}. Then I_{x}=I_{y}=\dfrac{1}{2}I_{O}=\dfrac{1}{2}\!\left( \dfrac{\pi a^{4}\rho }{2} \right) =\dfrac{\pi a^{4}\rho }{4}
NOW WORK
In dynamics, the moment of inertia of a lamina occurs in connection with the study of rotational motion. If a rigid object (a lamina) is rotated about an axis a with angular speed \omega , then its rotational kinetic energy K is given by \bbox[5px, border:1px solid black, #F9F7ED]{ K=\dfrac{1}{2}I_{a}~\omega ^{2} }
For example, suppose the homogeneous lamina in Example 3 has mass density \rho =20\text{kg}/\text{m}^{2} and radius a=1\text{m}. If it is rotated about the origin at the constant angular speed \omega =2\pi \text{rad}/\text{s}, then its kinetic energy K is K=\dfrac{1}{2}I_O \omega ^{2}=\dfrac{1}{2}\!\left( \dfrac{\pi a^{4}\rho }{2}\right) ( 2\pi ) ^{2}\underset{\underset{\color{#0066A7}{\hbox{\(a=1;\rho =20\)}}}{\color{#0066A7}{\uparrow }}}{=}\dfrac{1}{2}( 10\pi ) ( 4\pi ^{2}) =20\pi ^{3}\dfrac{\text{kg}/\text{m}^{2}}{\text{s}^{2}}
Observe the similarity between the formula for rotational kinetic energy K presented here and the formula for the kinetic energy K of an object of mass m moving in a straight line with speed v, namely, K=\dfrac{1}{2} mv^{2}.