3.3 Derivatives of Logarithmic FunctionsPrinted Page 222
222
OBJECTIVES
When you finish this section, you should be able to:
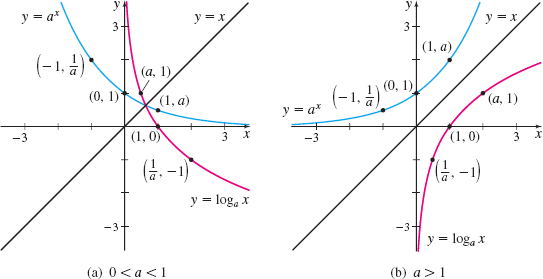
Recall that the function f(x)=ax, where a>0 and a≠1, is one-to-one and is defined for all real numbers. We know from Section 3.1 that f′(x)=axlna and that the domain of f′(x) is also the set of all real numbers. Moreover, since f′(x)≠0, the inverse of f, y=logax, is differentiable on its domain (0,∞). See Figure 5.
NEED TO REVIEW?
Logarithmic functions are discussed in Section P.5, pp. 42-45.
1 Differentiate Logarithmic FunctionsPrinted Page 222
To find y′=ddxlogax, we use the fact that the following statements are equivalent: y=logaxif and onlyifx=ay
Now we differentiate the equation on the right using implicit differentiation. ddxx=ddxay1=aylnadydxUse the Chain Rule on the right. dydx=1aylnaSolve fordydx.dydx=1xlnax=ay
THEOREM Derivative of a Logarithmic Function
The derivative of the logarithmic function y=logax, x>0, a>0, and a≠1, is \begin{equation*} \bbox[5px, border:1px solid black, #F9F7ED]{ y^\prime =\dfrac{d}{dx}\log _{a}x=\dfrac{1}{x\ln a}\qquad x > 0}\tag{1} \end{equation*}
When a=e, then \ln a=\ln e=1, and (1) gives the formula for the derivative of the natural logarithm function f( x) =\ln x.
THEOREM Derivative of the Natural Logarithm Function
The derivative of the natural logarithm function y=\ln x, x>0, is \bbox[5px, border:1px solid black, #F9F7ED]{ y^\prime =\dfrac{d}{dx}\ln x=\dfrac{1}{x}}
223
EXAMPLE 1Differentiating Logarithmic Functions
Find y^\prime if:
- (a) y= (\ln x)^{2}
- (b) y=\dfrac{1}{2}\log x
- (c) \ln x+\ln y=2x
Solution (a) We use the Power Rule for Functions. Then \begin{eqnarray*} && y^\prime =\dfrac{d}{dx}( \ln x) ^{2} \underset{\underset{\color{#0066A7}{\hbox{\(\tfrac{d}{dx}[u(x) ] ^{n}{=n}[u(x) ]^{n-1}\tfrac{du}{dx}\)}}}{\color{#0066A7}{\uparrow}}}{=} 2\ln x\cdot \dfrac{d}{dx}\ln x= (2\ln x)\left(\dfrac{1}{x}\right)=\dfrac{2\ln x}{x}\\ \end{eqnarray*}
(b) Remember that \log x=\log _{10}x. Then y=\dfrac{1}{2}\log x=\dfrac{1}{2}\log_{10} x. \begin{eqnarray*} && y^\prime =\dfrac{1}{2}\left( \dfrac{d}{dx}\log_{10} x\right) = \dfrac{1}{2}\cdot \dfrac{1}{x\ln 10}=\dfrac{1}{2x\ln 10}\qquad {\color{#0066A7}{\tfrac{d}{dx}\log_{a}{x} = \tfrac{1}{x\ln a}}} \end{eqnarray*}
(c) We assume y is a differentiable function of x and use implicit differentiation. Then \begin{eqnarray*} \begin{array}{rl@{\quad}l} \dfrac{d}{dx}\left( \ln x+\ln y\right) &= \dfrac{d}{dx}(2x) \\ \dfrac{d}{dx}\ln x+\dfrac{d}{dx}\ln y &= 2 \\ \dfrac{1}{x}+\dfrac{1}{y}\dfrac{dy}{dx} &= 2 & {\color{#0066A7}{\tfrac{d}{dx}\ln {y}=\tfrac{1}{y}\tfrac{dy}{dx}}}\\ y^\prime &= \dfrac{dy}{dx}=y\left(2-\dfrac{1}{x}\right) =\dfrac{y\left(2x-1\right)}{x} & {\color{#0066A7}{\hbox{Solve for}\quad {y^\prime }=\tfrac{dy}{dx}.}} \end{array} \end{eqnarray*}
NOW WORK
If y=\ln [u(x) ] , where u=u( x) >0 is a differentiable function of x, then by the Chain Rule, \begin{eqnarray*} \dfrac{dy}{dx} = \dfrac{dy}{du}\cdot \dfrac{du}{dx}=\dfrac{1}{u}\dfrac{du}{dx}=\dfrac{u^\prime(x)}{u(x)} \end{eqnarray*} \bbox[5px, border:1px solid black, #F9F7ED]{ \dfrac{d}{dx} \ln [u(x)] =\dfrac{u^\prime(x)}{u(x)} }
EXAMPLE 2Differentiating Logarithmic Functions
Find y^\prime if:
- (a) y=\ln (5x)
- (b) y=x\ln (x^{2}+1)
- (c) y=\ln \vert x\vert
Solution
(a) \begin{eqnarray*} && y^\prime = \dfrac{d}{dx}\ln (5x) = \dfrac{\dfrac{d}{dx}(5x) }{5x}=\dfrac{5}{5x} = \dfrac{1}{x} \qquad {\color{#0066A7}{\tfrac{d}{dx}\ln u({x}) = \tfrac{u^\prime (x)}{u(x)}}} \end{eqnarray*}
(b) \begin{eqnarray*} y^\prime = \dfrac{d}{dx}[ x\ln (x^{2}+1)] &=& x\dfrac{d}{dx} \ln (x^{2}+1) +\left( \dfrac{d}{dx}x\right) \ln (x^{2}+1)\qquad{\color{#0066A7}{\hbox{Product Rule}}} \\ &&\underset{\underset{\color{#0066A7}{\tfrac{d}{dx}\ln u(x)=\tfrac{u^\prime (x)}{u(x)}}}{\color{#0066A7}{\uparrow}}}{=} x\cdot \dfrac{\dfrac{d}{dx}(x^{2}+1) }{ x^{2}+1}+1\cdot \ln (x^{2}+1) =\dfrac{2x^{2}}{x^{2}+1}+\ln (x^{2}+1) \end{eqnarray*}
224
(c) \begin{eqnarray*} y &=&\ln \vert x\vert =\left\{ \begin{array}{c@{\quad}l} \ln x & \hbox{if}\; x>0 \\ \ln (-x) & \hbox{if}\; x<0 \end{array} \right. \\ y^\prime &=& \dfrac{d}{dx}\ln \vert x\vert =\left\{ \begin{array}{c@{\quad}l} \dfrac{1}{x} & \hbox{if}\;x>0 \\ \dfrac{1}{-x}(-1) =\dfrac{1}{x} & \hbox{if}\;x<0 \end{array}\right. \end{eqnarray*}
That is, \dfrac{d}{dx}\ln \vert x\vert =\dfrac{1}{x} for all numbers x≠ 0.
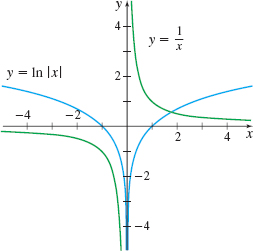
Part (c) proves an important result that is used often: \bbox[5px, border:1px solid black, #F9F7ED]{ \dfrac{d}{dx}\ln \vert x\vert =\dfrac{1}{x}\qquad x≠ 0}
Look at the graph of y=\ln \left\vert x\right\vert in Figure 6. As we move from left to right along the graph, starting where x is unbounded in the negative direction and ending near the y-axis, we see that the tangent lines to y=\ln \left\vert x\right\vert go from being nearly horizontal with negative slope to being nearly vertical with a very large negative slope. This is reflected in the graph of the derivative y^\prime =\dfrac{1}{x}, where x<0: The graph starts close to zero and slightly negative and gets more negative as the y-axis is approached.
Similar remarks hold for x>0. The graph of y^\prime =\dfrac{1}{x} just to the right of the y-axis is unbounded in the positive direction (the tangent lines to y=\ln \left\vert x\right\vert are nearly vertical with positive slope). As x becomes unbounded in the positive direction, the graph of y^\prime gets closer to zero but remains positive (the tangent lines to y=\ln \left\vert x\right\vert are nearly horizontal with positive slope).
NOW WORK
NEED TO REVIEW?
Properties of logarithms are discussed in Appendix A.1, pp. A-10 to A-11.
Properties of logarithms can sometimes be used to simplify the work needed to find a derivative.
EXAMPLE 3Differentiating Logarithmic Functions
Find y^\prime if y=\ln \left[ \dfrac{\left( 2x-1\right) ^{3}\sqrt{2x^{4}+1}}{x}\right]\!.
NOTE
In the remaining examples, we do not explicitly state the domain of a function containing a logarithm. Instead, we assume that the variable is restricted so all arguments for logarithmic functions are positive.
Solution Rather than attempting to use the Chain Rule, Quotient Rule, and Product Rule, we first simplify the right side by using properties of logarithms. \begin{eqnarray*} y &=& \ln \left[ \dfrac{\left( 2x-1\right) ^{3}\sqrt{2x^{4}+1}}{x}\right] =\ln \left( 2x-1\right) ^{3}+\ln \sqrt{2x^{4}+1}-\ln x\\ &=& 3\ln \left( 2x-1\right) + \dfrac{1}{2}\ln ( 2x^{4}+1) -\ln x \end{eqnarray*}
Now we differentiate y. \begin{eqnarray*} y^\prime &=&\dfrac{d}{dx}\left[ 3\ln \left( 2x-1\right) +\dfrac{1}{2}\ln ( 2x^{4}+1) -\ln x\right]\\ &=&\dfrac{d}{dx}\left[3\ln \left( 2x-1\right)\right] + \dfrac{d}{dx}\left[\dfrac{1}{2}\ln ( 2x^{4}+1)\right] -\dfrac{d}{dx}\ln x \\ &=&3\cdot \dfrac{2}{2x-1}+\dfrac{1}{2}\cdot \dfrac{8x^{3}}{2x^{4}+1}-\dfrac{1}{x}=\dfrac{6}{2x-1}+\dfrac{4x^{3}}{2x^{4}+1}-\dfrac{1}{x} \end{eqnarray*}
NOW WORK
2 Use Logarithmic DifferentiationPrinted Page 225
225
Logarithms and their properties are very useful for finding derivatives of functions that involve products, quotients, or powers. This method, called logarithmic differentiation, uses the facts that the logarithm of a product is a sum, the logarithm of a quotient is a difference, and the logarithm of a power is a product.
EXAMPLE 4Finding Derivatives Using Logarithmic Differentiation

Find y^\prime if y=\dfrac{x^{2}\sqrt{5x+1}}{( 3x-2) ^{3}}.
Solution It is easier to find y^\prime if we take the natural logarithm of each side before differentiating. That is, we write \ln y=\ln \left[ \dfrac{x^{2}\sqrt{5x+1}}{( 3x-2) ^{3}}\right]
ORIGINS
Logarithmic differentiation was first used in 1697 by Johann Bernoulli (1667–1748) to find the derivative of {y=x}^{x}. Johann, a member of a famous family of mathematicians, was the younger brother of Jakob Bernoulli (1654–1705). He was also a contemporary of Newton, Leibniz, and the French mathematician Guillaume de L’Hôpital.
and simplify the equation using properties of logarithms. \begin{eqnarray*} \ln y &=&\ln [ x^{2}\sqrt{5x+1}] -\ln ( 3x-2) ^{3}=\ln x^{2}+\ln (5x+1) ^{1/2}-\ln ( 3x-2) ^{3} \\ &=&2\ln x+\dfrac{1}{2}\ln (5x+1) -3\ln ( 3x-2) \end{eqnarray*}
To find y^\prime, we use implicit differentiation. \begin{eqnarray*} \dfrac{d}{dx}\ln y&=&\dfrac{d}{dx}\left[ 2\ln x+\dfrac{1}{2}\ln (5x+1) -3\ln (3x-2) \right]\\ \dfrac{y^\prime}{y}&=&\dfrac{d}{dx}(2\ln x) + \dfrac{d}{dx} \left[\dfrac{1}{2}\ln (5x+1)\right]-\dfrac{d}{dx}[3\ln(3x-2)]\\ &=&\dfrac{2}{x}+\dfrac{5}{2 ( 5x+1) }-\dfrac{9}{3x-2} \\ y^\prime &=&y\!\left[ \dfrac{2}{x}+\dfrac{5}{2 ( 5x+1) }-\dfrac{9}{3x-2}\right] \!=\!\left[ \dfrac{x^{2}\sqrt{5x+1}}{( 3x-2) ^{3}}\right]\!\! \left[ \dfrac{2}{x}+\dfrac{5}{2(5x+1) }-\dfrac{9}{3x-2}\right] \end{eqnarray*}
Summarizing these steps, we arrive at the method of Logarithmic Differentiation.
Steps for Using Logarithmic Differentiation
Step 1 If the function y=f( x) consists of products, quotients, and powers, take the natural logarithm of each side. Then simplify the equation using properties of logarithms.
Step 2 Differentiate implicitly, and use the fact that \dfrac{d}{dx}\ln y=\dfrac{y^\prime }{y}.
Step 3 Solve for y^\prime , and replace y with f( x) .
NOW WORK
EXAMPLE 5Using Logarithmic Differentiation
Find y^\prime if y=x^{x}, x>0.
Solution Notice that x^{x} is neither x raised to a fixed power a, nor a fixed base a raised to a variable power. We follow the steps for logarithmic differentiation:
Step 1 Take the natural logarithm of each side of y=x^{x}, and simplify: \ln y=\ln x^{x}=x\ln x
226
Step 2 Differentiate implicitly. \begin{eqnarray*} \dfrac{d}{dx}\ln y&=&\dfrac{d}{dx}(x\ln x)\\ \dfrac{y^\prime }{y} &=& x\cdot \dfrac{d}{dx}\ln x+\left( \dfrac{d}{dx}x\right) \cdot \ln x=x\left(\dfrac{1}{x}\right) +1\cdot \ln x=1+\ln x \end{eqnarray*}
Step 3 Solve for y^\prime : y^\prime =y( 1+\ln x) =x^{x}( 1+\ln x).
A second approach to finding the derivative of y=x^{x} is to use the fact that y=x^{x}= e^{\ln {x}^{{x}}}=e^{x\ln x}. See Problem 85.
NOW WORK
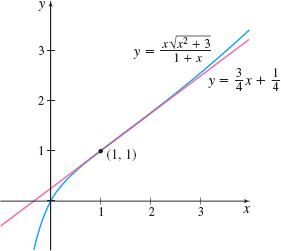
EXAMPLE 6Finding an Equation of a Tangent Line
Find an equation of the tangent line to the graph of f( x) =\dfrac{x\sqrt{x^{2}+3}}{1+x} at the point (1,1) .
Solution The slope of the tangent line to the graph of y=f( x) at the point (1,1) is f^\prime (1) . Since the function consists of a product, a quotient, and a power, we follow the steps for logarithmic differentiation:
Step 1 Take the natural logarithm of each side, and simplify: \ln y=\ln \dfrac{x\sqrt{x^{2}+3}}{1+x}=\ln x+\dfrac{1}{2}\ln ( x^{2}+3) -\ln ( 1+x)
Step 2 Differentiate implicitly. \dfrac{y^\prime }{y}=\dfrac{1}{x}+\dfrac{1}{2}\cdot \dfrac{2x}{x^{2}+3}- \dfrac{1}{1+x}=\dfrac{1}{x}+\dfrac{x}{x^{2}+3}-\dfrac{1}{1+x}
Step 3 Solve for y^\prime and simplify: y^\prime =f^\prime (x) = y\left( \dfrac{1}{x}+\dfrac{x}{x^{2}+3}-\dfrac{1}{1+x}\right) = \dfrac{x\sqrt{x^{2}+3}}{1+x}\left( \dfrac{1}{x}+\dfrac{x}{x^{2}+3}-\dfrac{1}{1+x}\right)
Now we find the slope of the tangent line by evaluating f^\prime (1) . f^\prime (1) =\dfrac{\sqrt{4}}{2}\left( 1+\dfrac{1}{4}-\dfrac{1}{2}\right) =\dfrac{3}{4}
Then an equation of the tangent line to the graph of f at the point (1,1) is \begin{eqnarray*} y-1 &=&\dfrac{3}{4}( x-1) \\ y &=&\dfrac{3}{4}x+\dfrac{1}{4} \end{eqnarray*}
See Figure 7 for the graphs of f and y=\dfrac{3}{4}x+\dfrac{1}{4}.
NOW WORK
We now prove the Power Rule for finding the derivative of y=x^{a}, where a is a real number.
THEOREM Power Rule
If a is a real number, then \bbox[5px, border:1px solid black, #F9F7ED]{ \dfrac{d}{dx}x^{a}=ax^{a-1}}
227
Proof
Let y=x^{a}, a real. Then \ln y=\ln x^{a}=a\ln x. \begin{eqnarray*} \frac{y^\prime }{y} &=&a\frac{1}{x} \\ y^\prime &=&\frac{ay}{x}=\frac{ax^{a}}{x}=ax^{a-1} \end{eqnarray*}
EXAMPLE 7Using the Power Rule
Find the derivative of:
- (a) y=x^{\sqrt{2}}
- (b) y=(x^{2}+1) ^{\pi}
Solution
- (a) We differentiate y using the Power Rule. y^\prime =\frac{d}{dx}x^{\sqrt{2}}=\sqrt{2}x^{\sqrt{2}-1}
- (b) The Power Rule for Functions also holds when the exponent is a real number. Then y^\prime =\frac{d}{dx}(x^{2}+1) ^{\pi }=\pi (x^{2}+1) ^{\pi -1}(2x) =2\pi x(x^{2}+1) ^{\pi-1}
3 Express e as a LimitPrinted Page 227
In Section P.5, we stated that the number e has this property: \ln e=1. Here are two equivalent ways of writing e as a limit, both of which are used in later chapters.
THEOREM The Number e as a Limit
The number e can be expressed by either of the two limits: \bbox[5px, border:1px solid black, #F9F7ED]{ \hbox{(a)} \lim\limits_{h\rightarrow 0}(1+h)^{1/h} = e \qquad \hbox{or}\qquad \hbox{(b)} \lim\limits_{n\rightarrow ∞ }\left( 1+\dfrac{1}{n}\right) ^{n}=e}\tag{2}
Proof
(a) The derivative of f(x) =\ln x is f^\prime (x) =\frac{1}{x} so f^\prime (1) =1. Then \begin{eqnarray*} f^\prime (1) \underset{\underset{\color{#0066A7}{\hbox{Definition of a Derivative}}}{\color{#0066A7}{\uparrow}}}{=} \lim\limits_{h\rightarrow 0}\frac{f(1+h) -f(1) }{h} &=&\lim\limits_{h\rightarrow 0}\dfrac{\ln (1+h) -\ln 1}{h} = \lim\limits_{h\rightarrow 0}\frac{\ln (1+h) -0}{h} \\ &=&\lim\limits_{h\rightarrow 0}\left[ \dfrac{1}{h}\ln (1+h) \right] =\lim\limits_{h\rightarrow 0}\ln (1+h) ^{1/h} \end{eqnarray*}
Since y=\ln x is continuous and f^\prime (1) =1, \lim\limits_{h\rightarrow 0}\ln (1+h) ^{1/h}=\ln \left[ \lim\limits_{h\rightarrow 0}(1+h) ^{1/h}\right] =1
Since \ln e=1, \ln \left[ \lim\limits_{h\rightarrow 0}(1+h) ^{1/h}\right] =\ln e
| n | \left(1+\frac{1}{n}\right)^{n} |
|---|---|
| 10 | 2.\, 593\,742\,46 |
| 1000 | 2.\, 716\,923\,932 |
| 10,000 | 2.\, 718\,145\,927 |
| 10^{6} | 2.\, 718\,280\, 469 |
Since y=\ln x is a one-to-one function, \lim\limits_{h\rightarrow 0}(1+h) ^{1/h}=e
(b) The limit derived in (a) is valid when h\rightarrow 0^{+}. So if we let n=\dfrac{1}{h}, then as h\rightarrow 0^{+}, n= \dfrac{1}{h}\rightarrow \infty and e=\lim\limits_{n\rightarrow \infty }\left( 1+\dfrac{1}{n}\right) ^{n}
Table 2 shows the values of \left( 1+\dfrac{1}{n}\right) ^{n} for selected values of n.
228
NOTE
Correct to nine decimal places, e= 2.\;718\;281\;828.
EXAMPLE 8Expressing a Limit in Terms of e
Express each limit in terms of the number e:
- (a) \lim\limits_{h\rightarrow 0}( 1+2h) ^{1/h}
- (b) \lim\limits_{n\rightarrow \infty}\left( 1+\dfrac{3}{n}\right) ^{2n}
Solution (a) This limit resembles \lim\limits_{h\rightarrow 0}(1+h) ^{1/h}, and with some manipulation, it can be expressed in terms of \lim\limits_{h\rightarrow 0}(1+h) ^{1/h}. ( 1+2h) ^{1/h}= [ ( 1+2h) ^{1/( 2h) } ] ^{2}
Now let k=2h, and note that h\rightarrow 0 is equivalent to 2h=k\rightarrow 0. So, \begin{eqnarray*} && \lim\limits_{h\rightarrow 0}( 1+2h) ^{1/h}=\lim\limits_{k\rightarrow 0}\left[ \left( 1+k\right) ^{1/k}\right] ^{2}=\left[ \lim\limits_{k\rightarrow 0}\left( 1+k\right) ^{1/k}\right] ^{2} \underset{\underset{\color{#0066A7}{\hbox{\((2)\)}}}{\color{#0066A7}{\uparrow}}}{=} e^{2} \\[-10pt] && \end{eqnarray*}
(b) This limit resembles \lim\limits_{n\rightarrow \infty} \left( 1+\dfrac{1}{n}\right) ^{n}. We rewrite it as follows: \left( 1+\dfrac{3}{n}\right) ^{2n}=\left[ \left( 1+\dfrac{3}{n}\right) ^{2n} \right] ^{3/3}=\left[ \left( 1+\dfrac{3}{n}\right) ^{n/3}\right] ^{6}
Let k=\dfrac{n}{3}. Since n\rightarrow \infty is equivalent to \dfrac{n }{3}=k\rightarrow \infty \,, we find that \begin{eqnarray*} && \lim\limits_{n\rightarrow \infty }\left( 1+\dfrac{3}{n}\right) ^{2n}=\lim\limits_{k\rightarrow \infty }\left[ \left( 1+\dfrac{1}{k}\right) ^{k}\right] ^{6}=\left[ \lim\limits_{k\rightarrow \infty }\left( 1+\dfrac{1}{ k}\right) ^{k}\right] ^{6} \underset{\underset{\color{#0066A7}{\hbox{\((2)\)}}}{\color{#0066A7}{\uparrow}}}{=} e^{6} \end{eqnarray*}
NOW WORK
The number e occurs in many applications. For example, in finance, the number e is used to find continuously compounded interest. See the discussion preceding Problem 89.